2021年新高考Ⅰ卷第21题的关联性研究

王小国 童继稀

(1.湖南省常宁市第二中学 2.湖南省长沙市雷锋学校)

高考真题背后往往蕴含着丰富的数学背景和知识结构,深入研究这些问题,对提高同学们的解题能力、思维素养有着深远的意义.本文给出2021年新高考Ⅰ卷第21题第(2)问的3种求解方法,并结合试题结构进行关联性拓展研究,以期拓宽大家的视野,提升研究精神.

1 真题呈现

本题充分体现了解析几何解答题起点低、落差高、设问有梯度的命题特点,发挥了数学学科高考的选拔性功能.第(1)问可以利用定义法求曲线方程,考查了对双曲线的概念理解,注意点M的轨迹只是双曲线的一支.第(2)问对考生的思维能力要求很高,主要考查了考生的数学运算与转化能力,求解困难表现在:1)坐标字母多,考生处理时有畏惧心理;2)式子井然有序,颇有规律,但结构复杂;3)动态变化之中的定值问题,需要探索,对考生的运算及转化能力要求较高.

2 解法赏析

3 关联性探究

3.1 背景溯源

由|TA|·|TB|＝|TP|·|TQ|的代数结构,我们容易联想到初中的割线定理与相交弦定理.

定理1(割线定理或相交弦定理)直线AB与CD交于点P,则A,B,C,D四点共圆的充要条件是

在解析几何有关四点共圆的证明中,我们有以下一个非常简洁的充要条件.

定理2若两条直线y＝kix＋bi(i＝1,2)与圆锥曲线ax2＋by2＋cx＋dy＋e＝0(a≠b)有四个交点,则四个交点共圆的充要条件是k1＋k2＝0.

实际上,真题中的A,B,P,Q应四点共圆,即圆与圆锥曲线相交于四点.在高中数学解析几何中的相关四点共圆问题,很多文献已作详述.

3.2 教材链接与高考命题特点

以四个共圆的点满足的关系为命题条件或结论,在教材、高考真题中经常出现.

例1(人教A 版高中数学《选修4-4》第38页例4)如图1所示,AB,CD是中心为点O的椭圆的两条相交弦,交点为P.两弦AB,CD与椭圆长轴的夹角分别为∠1,∠2,且∠1＝∠2,求证:|PA|·|PB|＝|PC|·|PD|.

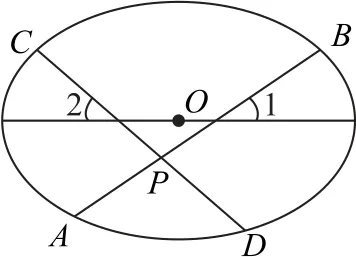
图1

题中的条件∠1＝∠2,即为直线AB与CD的斜率互为相反数,从而有|PA|·|PB|＝|PC|·|PD|.

当两直线的斜率不满足该关系时,我们可推广得到以下一般结论.

证明过程略.

当定理1中的C,D两点重合,即直线CD为圆的切线时,便可得到切割线定理.令T为切点,则|PT|2＝|PA|·|PB|.以此式结构拓展到椭圆中,有以下高考题.

例3(2016年四川卷理20,节选)已知椭圆E:的两个焦点与短轴的一个端点是直角三角形的3个顶点,直线l:y＝－x＋3与椭圆E有且只有一个公共点T.设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的两点A,B,且与直线l交于点P.证明:存在常数λ,使得|PT|2＝λ|PA|·|PB|,并求λ的值.

由于椭圆是由圆进行伸缩变换所得,故非平行的等长线段在同一伸缩变换作用下所得线段长度不一定相等.也就是说圆的切割线定理中的割线任意性,在椭圆中会受到一定条件的限制,这就是椭圆的“类切割线定理”.我们也可推广得到如下结论.

结论2已知倾斜角为α的直线l1与椭圆E:(a＞0,b＞0)相切于点T,过直线l1上的任意一点P,作倾斜角为β的直线l2与椭圆E交于不同的两点A,B,则

3.3 类似条件结构的处理技巧延伸

在高考真题中,对于类似的多线段长度比例式或乘积式结构,我们同样可以借助弦长公式处理,可以转化为向量处理,也可以利用投影转化为某个坐标的代数式予以处理,还可以根据参数方程中参数的几何意义求解,利用一些几何定理及性质予以转化.

3.4 类似结论关联下的性质探索

结论3若点A,B,C为圆锥曲线上三点,A为定点,且kAB＋kAC＝0,则kBC为定值.

该结论在圆中显然成立,为了突出问题,以下我们转化为在椭圆、双曲线与抛物线中来体现结果.

4 小结

著名的数学教育家波利亚曾说过,解题就像采蘑菇,当我们发现一个蘑菇时,它的周围可能就有一个蘑菇圈.本题便是一个极为漂亮的“蘑菇”.

首先,它根植于教材,教材不仅是基础知识与思想方法的重要载体,还是高考命题的主要依据与来源.如该真题的结构模型,本质是对四点共圆问题的考查,源自教材,又高于教材,切中考生的“软肋”:多字母运算处理,复杂结构的转化,动态问题的探究.因此,我们要重视教材中一些重要素材的研究与挖掘.

再者,我们在解题时,要回归本源,高考真题并非无源之水.解析几何问题,往往立意深刻,蕴藏着丰富的几何背景及规律.而追根溯源,在研究与挖掘、拓展与延伸中,采到“蘑菇圈”,不仅可掌握此类问题的基本处理方法,还能感受到思维、结构与逻辑的奇妙与美,提升思维素养,促进深度学习,把握问题的本质.

最后,我们要重视数学问题间蕴藏的关联性、相似(近)性,要善于链接教材、链接高考、链接竞赛、链接方法、链接思维等,通过具体案例寻找研究对象内在的联系,如知识结构、代数结构、条件层面、结论层面、问题背景、解题思路之间的联系等,再总结共性,融会贯通,学以致用,以至于把握数学的整体规律,提升对学科整体认识的高度、广度以及深度.

(完)