浅析小学生几何直观能力的培养措施


[摘 要] 几何直观能力对学生的数学学习具有重要意义,它是认识与理解数学的基础。实践证明,在概念教学、算理教学以及解题教学等环节中渗透数形结合思想,能有效地提高学生的几何直观能力,为学生核心素养的形成奠定基础。
[关键词] 几何直观;能力;培养;措施
几何直观是指借助几何的直观性描述与分析问题,将复杂的数学问题简单化、形象化,有助于学生获得解决问题的思路,从而提前预测出结果。小学数学教材中并没有直接涉及“几何直观”的具体内容,但《义务教育数学课程标准(2022年版)》对培养学生的几何直观能力有明确要求。为此,笔者做了大量研究,现整理成文,与读者共勉。
一、理论基础
荷兰学者范希尔夫妇和艾伦·霍弗提出的几何思维水平体系,是对几何直观理论体系较早且较权威的说明。范希尔夫妇将几何思维水平分为五级(见表1)。实践证明,小学二年级学生一般对应表格中的二级水平,但初中学生却难以达到四级水平。因此,他们在原有的理论基础上,把几何思维合并为直观、描述与理论水平三方面。
艾伦·霍弗从直观方面出发,针对直观化能力总结出五级理论(见表2)。
该理论已成为研究几何直观的重要理论基础,对培养学生的几何直观能力具有明显的导向作用。
二、培养措施
(一)注重概念教学,渗透几何直观
概念犹如打开知识大门的钥匙,既是同类事物的共同本质,又是同类事物的一般特征。数学概念是学生构成数学知识的基础,数学概念的建立是学生解决数学问题的前提。学生学习数学概念的情况好与不好,不但直接关系到学生数学知识的巩固,而且直接关系到学生数学理解能力的发展。
数学概念中的一些关键词,通常体现数学概念的基本含义。在数学概念的教学中,教师要把一个个关键词看作一个个点,认真地分析和讲解,并加以串联。如果把基本含义丢失了,学生对数学概念就难以完整识记、理解和把握。因此,在分析、讲解和串联关键词时,教师应根据教学内容、教学要求、教学任务的不同,仔细分析、精心讲解、巧妙串联,特别是概念的讲解,应讲得通俗、讲得透彻、讲得有趣,尽量避免过于抽象化。
有些教师不重视数学概念的教学,往往是先直接给出数学概念,再给学生讲解例题,然后让学生做习题,最后让学生背数学概念。像这样的数学概念教学,学生缺少认识、分析、理解概念本质特征的机会,使数学概念教学严重偏离正确的轨道。因此,对于数学概念的教学,教师应做到“三利用”:
一是利用已学概念学习新的概念。随着学生数学学习的逐步深入,数学知识的逐步积累,数学智力的逐步发展,教师应指导学生利用已学概念学习新的概念。
二是利用直观手段讲解概念。在数学概念教学中,教师应根据不同的数学概念,利用教具、模型、多媒体等直观形象的教学手段,把抽象的数学概念形象化,把深奥的数学概念通俗化。
三是利用概念本质讲透概念。利用数学概念的本质,把数学概念讲透,通常需要教师充分揭示數学概念的本质,充分讲清数学概念的联系,充分比较数学概念的异同。
数学概念具备“数”与“形”的双重特征。在概念教学中,教师应引导学生从这两个方面着手分析,有意识地在概念教学中渗透几何直观的思维。尤其是一些文字表达过于冗长的概念,教师可借助直观的图形辅助教学,让学生对概念产生直观形象的认识。这种教学方式,符合小学生的思维特征,对提高学生的理解能力具有直接的帮助。更重要的是能让学生在数形结合的概念教学中,感知几何直观的魅力。
案例1 “分数”的概念教学
在课堂导入环节引用诸如分生日蛋糕、切西瓜等生活情境,吸引学生的注意力,激发学生的探究欲。在学生对分数产生了探究兴趣时,教师结合数形结合思想,进行几何直观的渗透。
比如对1/2概念的认识,学生从生活情境中获得一定感悟后,教师可带领学生动手、动脑,进行实际操作。给每个学生分发一张A4纸,要求学生通过折纸的方式表达自己对1/2的理解。在学生能准确表达出1/2后,再鼓励学生尝试1/4、1/8、1/3等的折叠方法。
随着实践探索的深入,学生能准确表达出1/2的概念。在探索其他分数的折纸过程中,学生能积极开动脑筋,并主动合作交流,形成各种折叠方法。为了激发学生的几何直观能力,笔者要求学生紧扣分数的“数”与“形”两方面的特征,进行书写与表征,从根本上理解分数所表达的意义。
事实上,分数概念的教学,用几何图形的阴影部分面积表示分数与用分数表达几何阴影部分的面积,这两种训练方式能让学生在脑海中形成更为明确的直观图,帮助学生更好地理解分数的概念。本节课的教学任务在学生的操作、思考与探索中顺利完成。同时,学生的思维能力与几何直观能力,也随着实践活动的展开而得到有效提升。
(二)借助算理教学,培养几何直观能力
几何直观不但在图形和几何学习中会用到,而且在数与代数、统计与概率、综合与实践中也会用到。“数与代数”可分为数的认识、数的运算、常见的量和探索规律等知识板块,在这些知识板块上,每一个知识板块都可以培养学生的几何直观能力。
在教学“数的运算”时,很多教师只重视算法的教学,追求熟练计算,却忽视算理。其实,想让学生掌握算法,提高计算能力,既要引导学生熟练计算,又要引导学生理解算理。因为算理是算法的理论依据,算法是算理提炼和概括后形成的,算法和算理相辅相成,在加、减、乘、除四则运算教学中,教师都可以借助算理教学,培养学生的几何直观能力。
关于计算的算理教学,其几何直观的表现形式通常有三种:一种实物直观,二是简约符号直观,三是图形直观。
实物直观是借助实际的存在物,进行简捷的思考和形象的判断。既可以用实际的存在物演示,又可以用小棒和小画片等替代物演示,让学生边演示实物边理解算理。
简约符号直观是在头脑里建立图式表象。小学生的知觉和观察一般是从情绪性、无意性、不确定性向目标性、有意性、确定性的方向发展。对此,教师可借助算理教学,发挥简约符号直观的作用。
图形直观是借助几何图形对数学问题进行描述和分析。图形直观一般有“形形”和“数形”两种表示。在算理教学中,常采用“数形”表示,特别是分数四则运算的算理比较抽象,用“数形”表示,能使抽象的数学问题直观化。
对小学生而言,有些计算法则比较抽象,他们在理解上存在一定的难度。如果教师运用传统的教学方式进行授课,难以让学生知其然且知其所以然。而教师借助几何模型引导学生在直观的观察中洞察算理的本质,能让学生深刻理解算理,灵活应用算理。因此,教师将算理与几何直观相结合进行教学,会有意想不到的教学效果。
案例2 “一个数除以分数”的教学
问题:丽丽花了2/3小时,走了2km的路程;花花用了5/12小时,走了5/6km的路程,她们两人,谁走路的速度更快些?
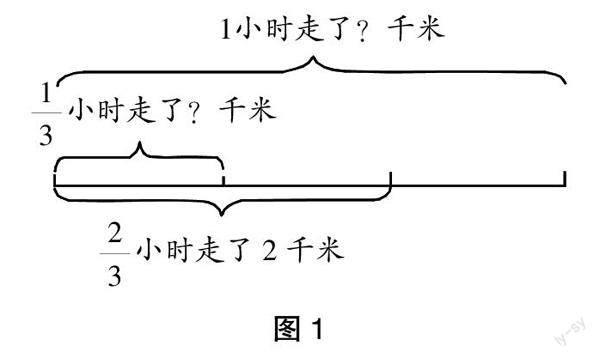
对于这个问题,学生列式基本都不成问题,问题在于列式后的计算。为了让学生从根本上掌握算理,笔者鼓励学生先画图,再计算。学生经思考后,绘制出图1,并根据此图进行算理的推导。
观察图1,将丽丽1小时所行走的路程分成了3份,丽丽花了2/3小时走完了2份路程的量,换个思维考虑,就是用2÷2来求出1/3小时行走的路程,再与3相乘即可,得到1小时所完成的路程为2÷2×3,也就是说被除数为分数时,先除以分子,再乘以分母。
画图的目的就在于引导学生明白为什么要这样计算,这样计算的过程是怎样的。如果教师直接将运算律灌输给学生,学生就只能机械地记忆,而不能形成深刻的认识。这种非理解性的记忆短暂且不牢固,会导致学生学了后面忘了前面。而利用几何直观,帮助学生理解算理的教学方式,会让学生弄明白为什么2÷(2/3)最后转化成了2×3/2,这种从根本上的理解性记忆是牢固的、永久的、可靠的。
通过以上教学可知,借助几何直观进行算理的教学,不仅是一种高效的教学方法,还是发展学生理解能力,提高学生思维水平的良好手段。学生通过这种教学方式,能从源头上理解算理的形成与发展过程,从而掌握其本质,这为后期更多、更复杂的数学学习奠定了坚实的基础。
(三)立足解题教学,培养几何直观能力
解题教学是数学教学的重要环节,教师应想方设法抓好解题教学这一环节,引导学生做到“三个应该”:
一是应该重视解题教学,解题教学的效果好与差,不但会直接影响学生对数学知识的运用,而且会直接影响学生解题能力的提升。因此,教师应引导学生重视解题教学,把解决问题作为数学学习的头等大事。
二是应该认真理解题意,解题教学得从理解题意入手,引领学生读懂题意,对于一些文字叙述多、综合性强、难度大的题目,要引导学生反复阅读、反复玩味、反复欣赏,认真理解题意。
三是应该寻找解题思路,引导学生挖掘数学题目中已知条件和所求问题的横向、纵向联系,从诸多思绪中梳理出一条条思想的纽带,再用这些纽带,把已学过的相关概念、公式、定理等数学知识连接起来,使问题得到解决。
立足解题教学培养学生几何直观能力,通常应在三个方面下功夫:
一是在直观教学方面下功夫,小学生的数学思维以形象思维为主,计算、证明和推理,都需要形象思维这个基础。通过直观教学,利用直观图形将抽象的數学问题形象化,将复杂的数学问题简单化,能帮助学生更好地理解数学题意,从而培养学生的几何直观能力。
二是在数形结合方面下功夫,数学的语言和符号较为抽象,不利于学生理解和掌握。利用数形结合的方式直观展现数学问题,能实现数与形的互相转化,阐明数学问题之间的内在联系,从而培养学生的几何直观能力;
三是在实践操作方面下功夫,基于小学生的思维特点,小学数学教学应重视学生的动手操作,它是培养学生几何直观能力的有效途径之一。教学中,教师要帮助学生建立“手和脑”之间的联系,通过开展有趣的、有效的动手操作实践活动,充分调动学生的直观想象。
为了加强学生对数学知识的应用,教师可通过一些解题训练强化学生对基本图形的认识。小学阶段,学生所接触到的基本图形主要有线段、数轴、长方形、正方形或圆等,通过对这些图形问题的发现与描述,能增强学生对知识的理解程度,强化记忆效果,这也是培养学生几何直观能力的关键措施。
案例3 “鸡兔同笼”的解题教学
长方形是学生熟悉的一类基本图形,它的面积=长×宽。对于长方形的面积,教师可引导学生用“积=因素×因数”的形式来表达,这种表达常见的还有“总数=每份数×份数”。换个思维,生活中有很多实际问题的数量关系,可以转化成长方形的图形来进行表达。当繁杂的文字与数量关系转化为直观形象的长方形时,其中的关系则能让人一目了然,解题思路一旦明晰,问题也就迎刃而解了。教学中教师应尽可能地给学生创造思考与转化的机会,鼓励学生掌握数形转化的能力,为解题而服务。
“鸡兔同笼”是经典的数学问题,小学生不容易厘清其数量关系。笔者受到长方形面积的启发,将一道“鸡兔同笼”问题“8只鸡兔同笼,共26只脚,鸡兔各是几只”转化成了“长方形面积”问题。
第一步:如图2,引导学生先在草稿纸上画两个长方形,分别代表鸡脚和兔脚的数量,再将这两个长方形拼接在一块儿。
第二步,根据图中直观的数量关系,学生很快就能找到解决问题的办法。观察图2,可以看出兔脚数量的一半为26-2×8=10(只),兔脚总数为2×10=20(只),因此兔子的数量为2×10÷4=5(只);再观察鸡脚的数量为4×8-26=6(只),那么鸡的数量为6÷2=3(只)。简简单单的一张图,就将学生感到头疼的鸡兔同笼问题给解决了。
由此可以看出,解决数学问题应从多角度、多层次进行思考与分析,尤其是利用“形”的直观性来解决“数”的抽象性。将抽象的代数问题转化为直观的几何问题,能给学生一种主观的冲击,使他们又快又准地解题。
学生的解题能力,往往反映出学生的数学综合水平,将抽象的代数问题转化为直观的几何问题,不仅能实现快速解题的目的,还能活跃学生的思维,让学生在数形转化中形成创新能力。
总之,学生的几何直观能力的培养并非一朝一夕就能完成,它需要教师长期不懈地坚持、渗透。教师要从思想上高度重视学生几何直观能力的培养,并付诸实际教学,让几何直观在学生学习数学的各个阶段发挥其独有的价值,为学生形成良好的数学核心素养奠定基础。
作者简介:顾玮玮(1982—),本科学历,中小学一级教师,从事小学数学教学工作。

