单元整体视域下的菱形概念教学

［摘  要］ 数学概念教学，教师基于单元整体视角，以大概念所蕴含的思想和方法为驱动，激活学生的知识储备，创生数学现实，建立新概念的生成模型，为学生铺设探究新概念的路径；学生在有向开放的探究过程中生成概念，能培养高阶思维，发展核心素养.

［关键词］ 三会思想；单元整体；概念教学；数学现实

基金项目：江苏省教育科学“十四五”规划课题“基于核心素养的初中数学单元整体教学实践研究”（D/2021/02/136），徐州市教育科学“十四五”规划课题“‘三会思想统领下初中数学概念教学的立体化建构与实践探索”（GH14-21-L478）.

作者简介：魏宇亭（1981—），本科学历，中小学高级教师，从事初中数学教学工作，曾获江苏省第四届乡村骨干教师优秀课一等奖、徐州市优质课一等奖、徐州市带头优师、邳州市名师等奖项和荣誉.

引言

《义务教育数学课程标准（2022年版）》指出：改变过去注重以课时为单位的教学设计，推进单元整体教学设计，体现数学知识之间的内在逻辑关系，以及学习内容与核心素养表现的关联［1］. 教师要立足单元整体宏观视角，以单元核心概念为统领，贴合学生的认知规律；要立足数学现实创设教学情境，引导学生以单元核心概念所蕴含的思想和方法为驱动力，建构新概念的生成模型，用知识催生知识、用方法催生方法，形成生成概念、运用概念、回归概念的教学闭环. 在单元整体教学的提挈下，选用“数学现实”建构数学概念教学，能有效避免教学碎片化. 学生在有向开放的探究活动中，激活知识储备，建立新概念，重构概念群，感悟数学概念蕴含的思想和方法，感受概念螺旋生成过程，发展高阶思维以及数学核心素养. 基于上述对概念教学的理解，笔者在徐州市级教研活动中，执教苏科版八下（以下简称“教材”）“9.4  矩形、菱形、正方形”第3课时，得到与会师生的好评.

教材分析

1. 基于单元整体的教学分析

数学核心概念是一个拥有“核心”的“概念群”，是由核心概念及其生长出来的子概念组成的知识体系［2］. 本单元的标题为“中心对称图形——平行四边形”，教材分为5节，前两节分别为“图形的旋转”与“中心对称与中心对称图形”. 对教材进行结构化分析，中心对称与中心对称图形是本章的核心概念，子概念为平行四边形、矩形、菱形、正方形等，其中平行四边形又是其他几类图形的核心概念. 基于概念的群属关系、课堂教学的适切度，本课选用中心对称为单元核心概念，以其所蕴含的特殊的旋转思想和方法为驱动力，呈现由三角形形成平行四边形与矩形的范例，创设数学现实情境，建构菱形的概念.

2. 基于数学现实的教学分析

本课教学，教师更乐意选用生活现实创设教学情境，引导学生从生活现象中抽象出菱形，进而探究其概念和性质.这一方式，有交融生活与数学的优点，但容易孤立概念，偏离单元整体，造成知识碎片化的现象. 基于单元整体视域俯察章节体系，引导学生以核心概念为驱动力，选用数学现实创设教学情境，建立核心概念与子概念的线性关系，形成完备的概念体系，能有效规避上述问题.

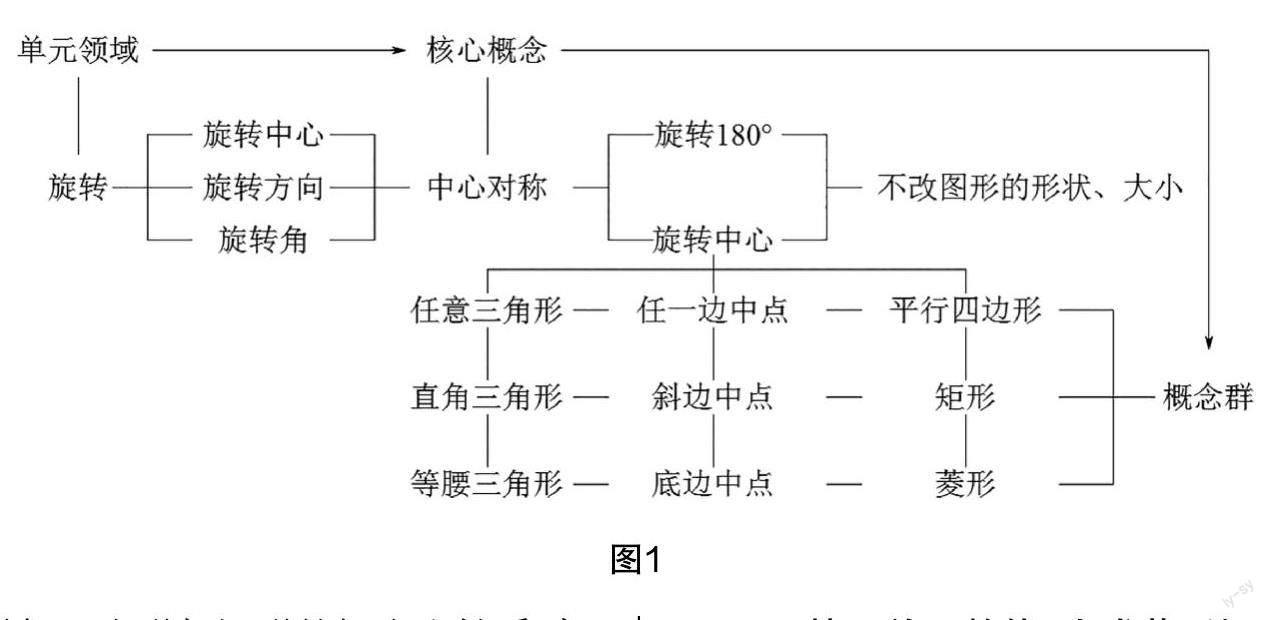
学生在七年级学过三角形的概念和性质，本单元已建立中心对称、平行四边形等概念，具备以中心对称这一核心概念为驱动力，建构菱形概念的数学现实. 基于单元整体，以中心对称为核心概念，立足数学现实，建立概念生成模型，铺设有向开放的探究路径，绘制成本课教学结构图（如图1所示）.

教学设计

1. 立足数学现实，创设教学情境

（1）导语：数学源于生活，也源于数学本身，前几节课，同学们学习了平行四边形与矩形的概念和性质，知道矩形是特殊的平行四边形.今天，我们从另一个视角，再认识这两种图形.

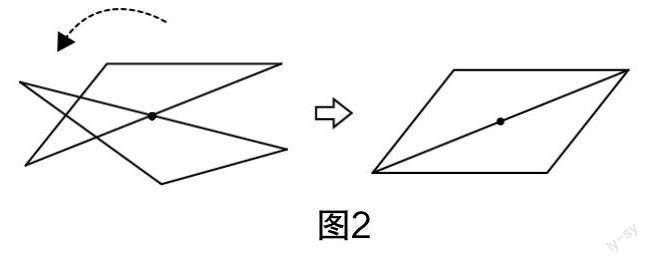
（2）如图2所示，用几何画板演示三角形的旋转过程，让学生观察并思考：

①请用数学语言，描述这种图形运动. ②你有哪些发现？

引导学生发现旋转中心所在的特殊位置，由三角形到平行四边形的转化过程.

（3）设问：可获得怎样的结论？

（4）如图3所示，用几何画板演示直角三角形的旋转过程，让学生观察并思考：①从旋转的要素和结果来看，你有哪些发现？②与图2相比，有哪些区别和联系？③在直角三角形中，以任一边的中点为旋转中心，旋转180°后与原图形组成的一定是矩形吗？为什么？

設计意图  通过旋转，动态演示由三角形生成平行四边形的过程，运用先行组织者技术，唤醒学生积累的知识和方法，创设从三角形与旋转中心的特殊性入手，探究菱形概念与性质的数学现实情境，以中心对称这一核心概念为驱动力，厘清核心概念与子概念的从属关系.

2. 基于单元整体，生成菱形概念

（1）设问：直角三角形是以角分类的特殊三角形；若以边分类，有什么样的特殊三角形？

（2）追问：基于特殊性考虑，旋转中心应定在什么位置？

（3）作图：如图4所示，画出以等腰三角形底边中点为旋转中心，旋转180°后的图形.

（4）设问：原三角形与旋转后的三角形组成了什么图形？

（5）设问：请用自己的语言描述该图形的特征，并说明理由.

（6）讨论归纳菱形概念：有一组邻边相等的平行四边形是菱形.

设计意图  学生基于数学现实，建立探究菱形概念的模型，通过作图，亲历菱形生成的过程；抓住等腰三角形两腰相等的性质，形成菱形概念.

3. 运用概念模型，探究菱形性质

（1）设问：等腰三角形具有哪些特殊性质？

（2）设问：猜想菱形会有哪些特殊性质，并说明理由.

（3）追问：菱形的特殊性与等腰三角形的特殊性有什么联系？

（4）小结菱形的性质.

（5）师生互动，用三种语言描述菱形的特殊性质（见表1）.

（6）追问：如图5所示，在菱形中发现了哪些特殊的三角形？它们之间有什么关系？

（7）追问：菱形是中心对称图形吗？是轴对称图形吗？请说明理由.

设计意图  如图6所示，以单元整体为引擎，以学生积累的等腰三角形知识以及中心对称思想方法为数学现实，在核心概念的驱动下，催生菱形的特殊性质.

4. 举一反三变式，巩固运用概念

（1）例题教学.

出示：如图7所示，木制衣帽架由3个全等的菱形构成，在A，E，F，C，G，H处安装上、下两排挂钩，可以根据需要改变挂钩间的距离，并在B，M处固定. 已知菱形ABCD的边长为13 cm，要使两排挂钩间的距离为24 cm，求B，M之间的距离.

①要求学生独立思考，寻找解决问题的方法.

②组织学生小组合作，随后分组展示解题思路.

③师生互动完成求解，形成将菱形转化为直角三角形的解题思路，体验化归思想.

（2）变式教学.

①在菱形ABCD中，若BD=10，AC=24，求菱形的边长.

②在菱形ABCD中，若BD=10，AC=24，求菱形的周长.

③在菱形ABCD中，若BD=10，AC=24，求菱形的面积.

（3）提炼求菱形面积的方法.

设计意图  运用菱形概念解决实际问题，通过变式教学，多维度搭建数学与生活的通道，拓展探究空间，发展学生以“三会”为代表的数学核心素养.

5. 回归生活现实，完善概念体系

（1）如图8所示，播放PPT，欣赏生活中的菱形.

（2）活动：学生列举生活中常见的菱形.

（3）组织学生从概念、数学思想方法等方面总结本课.

（4）以抢答的形式，完成课堂检测和巩固.

（5）课后思考：用本课的探究思路，尝试获取正方形的概念和性质.

设计意图  向学生展示含菱形的图片，引导学生列举生活中常见的菱形，在生活现实和数学现实的交融中，具象菱形概念，建立并完善概念体系，培养学生的高阶思维；在解决问题的过程中，激发单元整体教学的张力，形成完整的教学闭环.

6. 板书设计

见图9.

教学反思

1. 整体统领部分，核心驾驭群属

基于单元整体建构概念教学，应从整体性、关联性、独立性去分析单元与课时之间的关系，用整体统领部分，把脉某一概念的前承与后续；用核心概念驾驭群属，厘清上下位关系，形成结构化的概念群，达成化部分为整体，聚零散成群属，避免知识碎片化现象的产生. 宏观分析，初中数学可分为数与代数、图形与几何、统计与概率三大领域；中观分析，教材的每章是单元领域，它们从属上述三大领域；微观分析，在单元领域中，由核心概念统领概念群，核心概念是观念、策略、方法，是开展单元整体教学的切口，起着辐射整体、提挈下位的作用，用核心概念的思维和方法建构新概念教学，是开展单元整体教学的路径之一.

分析本章的教材结构可以发现，它先从生活现实抽象出平行四边形及矩形的概念，然后直接告知菱形与正方形的概念，之间的跨度较大，若就概念教概念，易偏离单元整体目标、忽视核心概念的价值. 基于上述所言，本课从中心对称这一核心概念中汲取思想和方法，创设由三角形生成平行四边形和矩形的情境，引导学生用批判性思维审视情境，以核心概念为驱动力，快速激活知识储备，形成由等腰三角形生成菱形、在菱形中发现特殊三角形的互逆视角，建立探究菱形概念与性质的教学模型.

2. 立足数学现实，汲取探究力量

数学现实是学生在学习过程中所积累的知识和方法，在核心概念的引领下，将数学思想方法、概念的生长点、概念群属关系、解决问题的通法、学生学业水平等进行关联和整合，创生基于单元整体的数学现实. 清晰诊断学生已有的知识和困难，确立学生已有知识的激活源，寻找新知识的类比源和生长源，不同知识点之间一以贯之的关联源［3］. 学生的数学现实蕴含着探究新知的蓬勃动力，是建立新概念的强大力量.

在本章中，学生学习了图形的旋转、中心对称、平行四边形和矩形，若本课仍从生活现实抽象菱形概念，容易孤立概念，错失建构单元整体的良机，产生知识碎片化的现象. 在本课教学中，从中心对称这一核心概念汲取原生力，创设从三角形动态生成平行四边形和矩形的情境；引导学生用批判性思维寻找共性和特性，激起新旧认知之间的对抗力；学生从三角形、中心对称等概念中提取知识和方法，建立研究菱形概念的模型，沿着有向开放的探究路径，汇聚探究内生力，形成基于单元整体的概念教学新样态.

3. 培育高阶思维，发展核心素养

促成高阶思维的学习追求不仅仅是在知识数量上的简单增加，更是能够建立起相互关联的基本知识结构框架［4］. 数学概念并不是孤立存在的，有其群属关系.因此概念教学应以单元核心概念为统领，建构下位概念，形成相互关联的概念框架.基于单元整体的概念教学，能培养学生的高階思维，发展学生的数学核心素养.

中心对称、平行四边形、菱形的概念之间有着层层递进的种属关系，既相互关联，又相对独立. 本课教学以中心对称所蕴含的思想和方法为驱动力，创设由三角形生成平行四边形、矩形的数学现实，类比建立探究菱形概念的模型；在“回归生活现实，完善概念体系”的环节中，引导学生回归生活现实再识菱形，彰显菱形概念的独立性. 学生在单元领域中，沿着用核心概念催生新概念的有向开放路径，经历聚合分散，深度建构概念框架，能充分挖掘数学概念所蕴含的思想和方法，增加概念教学的厚度.

结语

数学概念教学，教师“重解题、轻概念”的行为容易误导学生，使其认为数学只是解决“形结构”“式结构”的考试科目，由此缺少完整的概念体系和思想方法，对数学核心素养缺乏深层的理解，很难达成学科育人的目标. 基于单元整体，以核心概念所蕴含的思想和方法为驱动力，创设建构新概念的数学现实情境，让学生调动累积的知识和方法，催生新概念，完善概念体系，培养学生的高阶思维，发展学生的数学核心素养，可纠正“重解题、轻概念”的教学偏差.

参考文献：

［1］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［2］章建跃，宋莉莉，等. 美国高中数学核心概念图［J］. 课程·教材·教法，2013，33（11）：115-121.

［3］陈雪梅. 素养本位中学数学单元教学设计研究［M］. 上海：华东师范大学版社，2021.

［4］胡军. 高阶思维与初中数学课堂［M］. 上海：华东师范大学出版社，2021.