巧用“类比”提升初中数学复习品质
王占有
[摘 要] 类比思想是锻炼学生思维、促进概念深化、优化学生认知结构的重要手段. 在复习教学中,教师可以引导学生运用类比思想方法将那些相关或相似的知识有效地串联起来,以帮助学生构建完善的知识体系,并提高分析问题和解决问题的能力.
[关键词] 类比思想;思维;知识体系
类比是重要的数学教学手段,指根据两个对象的一些相同属性或相似属性,猜想它们其他的相同属性或相似属性,继而深刻理解这两个对象之间的内在联系和本质区别,以此获得深度理解. 类比教学是数学教学中一种重要的教学模式,其有利于培养学生思维的深刻性,有利于提高学生的分析能力和推理能力,有利于发展学生的自主学习能力.
复习课作为重要的数学课型,不像新知课那样具有诱惑力和挑战性,因此可能难以提起学生的兴趣. 为了提高学生的学习兴趣,教师不妨运用类比,通过对相似内容或相关内容的合理整合来丰富课堂教学内容,增强课堂的探究性,并通过有效的启发和引导达到巩固基础知识、拓宽数学思维、提升数学素养的目的. 类比的形式多种多样,如基本知识类比、知识结构类比、思维方式类比,但无论采用何种形式,教师都应结合教学实际,通过合理的整合和优化来提高类比教学的有效性.
基本知识类比
基本知识是数学知识的核心,是形成数学知识体系的要素. 扎实的基础是提升学生学习能力的前提,可见数学基本知识的教学是数学教学的重要一环. 在复习教学中,若对基本概念、基本计算原理等内容的复习仅停留在简单的知识罗列上,那恐怕难以激发学生的学习兴趣,而在教学中引导学生对相似的基本知识或相关的基本知识进行类比不失为一种有效的途径与方法.
1. 基本概念类比
基本概念在数学学习中的价值不言而喻——基本概念是解题的根本,是数学知识的核心. 在复习概念的过程中,教师若仅通过“师问生答”的方式逐条罗列概念等,不仅会让数学课堂更枯燥,还会因为没有合理整合知识,而使这些知识依然处于分散、无序的状态,不利于学生知识体系的建构. 在教学中,教师若能合理地引导学生进行类比,不仅可以帮助学生进一步理解概念的本质,而且可以使学生的思维变得更加有序,有利于提高知识的连贯性和完整性.
例如,复习四边形时,教师可以将平行四边形、矩形、菱形、正方形的概念放在一起综合分析,让学生主动探寻它们之间的区别与联系,引导学生通过添加条件完成不同图形的转化,以此让学生站在新视角分析概念,进一步理解概念的本质.
2. 基本计算原理类比
基本计算原理存在一定的相关性,借助类比,学生不仅能深刻地理解计算原理,而且能有效地总结不同计算方法之间的差异,这样可以有效地避免“张冠李戴”,能提高运算的正确率.
例如,复习一元一次不等式的解法时,教师可以引导学生类比一元一次方程的解法,以此让学生知晓它们的基本步骤是一致的,但依据不同,所以要正确理解它们性质的区别,且要注意不等号方向的变化. 上述对比分析,不仅能帮助学生巩固一元一次方程的知识,而且借助区别与联系可以让学生更清楚地进行计算.
知识结构类比
受学生知识水平、思维能力发展水平等因素的影响,教材在编排时可能会将一些相关的知识放在不同的章节中呈现,这样会让学生掌握相关知识时缺乏系统性、完整性. 所以为了帮助学生建构完善的知识体系,教师要认真研究教材,运用类比思想方法启发和引导学生将这些分散的知识通过横向拓展和纵向拓展有效地串联起来,从而建构完善的知识网络,提高学生的知识迁移能力.
1. 纵向类比
学生在解题时之所以无法快速、准确地找到解题的突破口,是因为学生没有形成完善的认知结构,对知识的理解不够深入,也就不能快速有效地检索出有价值的信息. 因此,在教学中,教师应想方设法帮助学生建构相对完善的认知结构,而类比不失为一种好方法. 纵向类比可以帮助学生形成知识板块,建构清晰的知识网络,提纲挈领地掌握已学知识,增强数学学习信心.
例如,复习“平移、轴对称、旋转”时,教师可以引导学生通过纵向类比掌握这三种变换的本质异同,从而深化对各知识板块的理解.
2. 横向类比
横向类比指有效沟通不同知识板块之间的联系,通过知识和方法的有效拓展、延伸,开阔学生的视野,丰富学生的解题思路,以此培养学生思维的灵活性和发散性.
例如,复习三角形内角和的证明时,教师可以让学生联想证明三角形外角和的方法,将内角和外角紧密地联系在一起,这样在解决内角或外角问题时,就可以通过互化高效地解决了.
思维方式类比
数学教学的实质是关于数学思维的教学,在教学中,教师要引导学生用数学思维去思考问题,用数学方法去解决问题. 在解决问题的过程中,学生可能会遇到这样或那样的问题,为了帮助学生突破障礙,教师可以引导学生类比相似或相关的问题,通过对原有知识、方法的拓展与延伸,找到解决问题的新路径,获得新知识,掌握新方法.
1. 特殊与一般的类比
特殊与一般是重要的数学思想方法. 我们在研究数学时大多从特殊出发,通过猜想、验证、归纳、总结,提取共性特征,最终形成一般性结论. 研究一些复杂的问题时,教师可以引导学生从特殊入手,先解决这个问题的特殊情况,然后类比特殊情况与一般情况,看看能否用解决特殊情况的方法和所得的结论来解决一般问题,由此将特殊情况与一般情况建立联系,从而借助特殊与一般的转化高效地解决问题.
例如,在小型会议上,每个到会人员都送给其他到会人员一件礼物,共送了90件礼物,问共有多少人参加会议.
解题时,教师可以引导学生与之前所学的“握手问题”相类比. 设有x人参加会议,每个人送的礼物为(x-1)件,于是x人共送出礼物x(x-1)件. 本题与“握手问题”具有共性特点,又有所不同——这里不需要除以2.
一般地,在教学中,从学生的已有认知出发,通过与特殊方法相类比,能找到解决此类问题的一般方法. 当然,在特殊与一般的类比中,我们既要找到对象的共同点,又要认清对象的本质区别,既要关注问题的共性,又要关注问题的个性,从而通过深入的探索与研究,让学生更好地理解知识、应用知识,进而有效地发展学生的数学思维.
2. “由此及彼”的类比
数学知识是相互联系的,对于一些相似问题,它们的研究方法也是相通的,因此在解决问题的过程中,教师要引导学生利用研究方法的相似性来研究一些相似问题或相关问题,以此获得新知识,掌握新技能.
例如,学习了“图形的相似”之后,教师可以引导学生结合探索三角形全等的经验,自主探究三角形相似的条件. 为了降低思维难度,提高学生自主探索新知识的热情,教师可以设计如下两个问题.
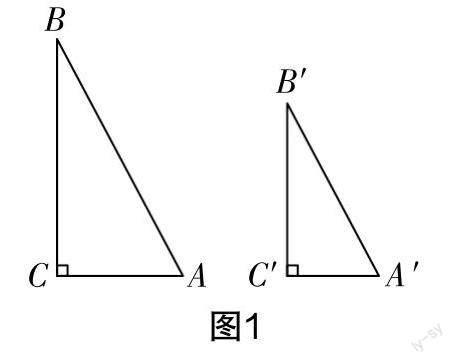
问题1:如图1所示,△ABC和△A′B′C′都是直角三角形,请结合证明两个直角三角形全等的经验,说一说满足什么条件可以使它们相似. (为了便于学生联想、类比,教师可点名让学生自己给出判定两个直角三角形全等的条件,并PPT呈现直角三角形全等的判定定理,进而让学生通过观察、分析,得到新结论)
问题2:请结合图1编写一道证明题,并写出完整的说理过程. 例如,如图1所示,已知_______,求证:Rt△ABC∽Rt△A′B′C′.
设计意图设计“问题1”的目的是通过与直角三角形全等条件相类比,得到结论“两直角边对应成比例或斜边和一条直角边对应成比例的两个直角三角形相似”. 设计“问题2”的目的是引导学生从特例出发,通过设参法,利用三角形相似的判定条件完成证明.
在探究新知的过程中,教师要引导学生类比“相似”与“全等”,既帮助学生巩固已学知识,又加速新知的生成,同时提高学生的数学探究能力,让学生在类比中掌握数学研究方法,提高自主学习能力.
总之,在复习教学中,教师要勇于创新,要改变传统的“炒冷饭”复习模式,为学生创设一个富有探究性的学习空间,引导学生通过类比认清知识之间的区别与联系,理解问题的本质特征,以此巩固知识,强化技能,提升素养. 同时,在教学中,教师要关注一些常规思路和常规方法,通过类比让学生能举一反三、融会贯通.

