流体微探力学性能高通量表征方法

赵 雷，刘 佳，任 群，杨 丽，王 辉，沈学静，贾云海，王海舟，

(1. 钢铁研究总院 北京材料基因工程高精尖创新中心，北京 100081) (2. 钢研纳克检测技术股份有限公司 金属材料表征北京市重点实验室，北京 100081) (3. 中国钢研科技集团数字化研发中心，北京 100081)

1 前 言

常规力学性能表征技术，包括宏观拉伸、压缩、弯曲、扭转以及冲击等方法，在新材料研发、性能优化、关键构件设计和服役评价等过程中具有极其重要的指导作用[1]。随着试验测试技术的不断进步，材料力学性能表征手段也逐步从宏观样品测试向微观样品测试领域拓展，陆续出现了小冲杆试验，拉伸、弯曲以及蠕变等小样品力学试验技术[2-6]。近年来，基于扫描电子显微镜(SEM)和透射电子显微镜(TEM)等电子显微技术，微纳尺度下实时观测材料拉伸和压缩的相关试验研究也得到了持续的发展[7]，由此可以在微观尺度上直接观测材料的变形破坏过程，为验证和澄清材料变形与破坏的内在机制提供直接证据，为材料宏观-微观的跨尺度表征提供技术支持。有限元分析也逐步受到广泛关注，结合多种测试方法获取的数据，有限元分析能够准确而有效地预测材料的力学性能[8]，是材料研究未来发展的一个方向。

硬度检测是最普遍且常用的力学性能分析方法[9，10]，一般使用一定的载荷将规定的压头压入被测材料，以材料表面局部塑性变形的大小评估被测材料的软硬。硬度测试技术在传统布氏、洛氏和维氏硬度测试等仪器化压入技术的基础上，发展出了显微维氏硬度、纳米压痕、原子力显微镜等深度-敏感压痕微观力学性能表征技术[11-13]。Li等[14]借助显微维氏硬度仪研究Fe-Al层状复合材料，发现不同厚度FeAl和FeAl2的显微组织对材料的脆性和韧性有显著影响。Chen等[15]利用显微硬度仪和纳米压痕法等手段对Zr52.5Cu17.9Ni14.6Al10Ti5非晶合金的研究结果表明，表面机械加工能提高合金微观结构均匀性，增大硬度并提高其韧性。Renner等[16]采用纳米压痕法对退火多晶镍进行研究，结果表明，晶体取向对材料的堆积方式和加工硬化行为有重要影响。Delincé等[17]对不同晶粒尺寸的双相钢进行了纳米压痕实验，通过改变压痕深度研究了压痕尺寸效应、晶粒尺寸效应、铁素体的加工硬化和马氏体强化等现象。以上研究说明，微观组织是影响金属材料硬度等力学性能的最主要因素，绝大多数材料均含有2种及以上微观组织相，不同相具有不同的性能。一般情况下，同一材料中珠光体的强度和硬度比铁素体要高，如果将相同加载力的压头分别施加在这2种微观组织上，珠光体的压痕比铁素体的小。但在实际情况下，金属材料的多种微观组织相互交织在一起，又同时受到外力作用发生塑性变形，其变形行为和机理相对复杂。材料的力学性能测试是研究在内应力和外施力共同作用下，物质结构和组织形态改变所引起的材料弹性和塑性变形、断裂和损伤机制[18-20]。通常，影响结构材料力学性能的内因主要有2个方面：一是物质结构，包括化学键性质和晶体结构，该因素决定了材料本征力学性能；二是组织形态，包括相分布、晶粒大小和形状、气孔大小和分布、杂质、缺陷等，它们对材料的性能影响极大[21]。现有力学性能表征手段虽然已经在一定程度上解决了材料力学性能测试过程中不同测试尺度(宏观-细观-微观测试)的可行性及准确性，然而，已有的拉伸、压缩、硬度等宏观和微观力学性能测试技术，都是基于对独立样件或样件离散点区域进行测试[22-24]，其宏观力学性能测试结果，通常只能给出厘米级尺寸样件整体的弹性极限、伸长率、弹性模量、拉伸强度、屈服强度等性能指标，无法给出该样品每个点或每个微区的微观力学性能[25，26]。另外，以纳米压痕试验技术为代表的细观和微观硬度测试手段，也只能通过多点测量的方式反映材料不同位置的微观硬度性能的差异，获得材料微米尺寸区域的弹性模量和屈服强度等性能指标，不能做到全连续状态分析[27]，更无法测量相邻2种微观组织同时受力时各自的形变情况。现有工业手段制备的宏观材料存在着非均匀性问题，通过对有限的、随机选择的点的性能测试，有可能造成材料不合格的部位被漏判，或者不合格结果被放大，导致整个材料被报废[28]。

流体微探力学性能高通量表征方法是一种从微观到宏观全连续跨尺度的无损力学性能统计分布表征方法[29]，是基于等静压原理[22]，采用高压水流体作为加载力，在保持各点压力均等及相同压力变化过程的情况下，通过金属材料表面微变形来表征材料硬度特征。冯光等[30]研究表明，高铬白口铸铁经冷等静压后表面形变的分布与碳化物等组织分布，Cu及Cr元素的成分分布，显微硬度和纳米压痕分布均具有高度相关性。Feng等[31，32]还采用激光增材制造技术制备了成分梯度分布的不锈钢样品，该样品经冷等静压后的表面形变分布与显微维氏硬度分布、奥氏体及铁素体组织分布等也具有高度的相关性。这2个实验均证明了对于同一个样品，材料表面的形变量越大，硬度越低，材料表面形变的分布也与显微组织的分布有关。但是，尚未证明具有不同特征微观组织的材料之间，表面形变量与硬度的相关性。本研究采用有限元方法模拟在等压力水流体加载下，具有不同硬度的显微组织的相互作用与塑性变形规律，并选取5种不同类型的金属材料，研究其表面形变量与硬度间的相关性。

2 实 验

实验选取具有不同硬度的金属样品5块，分别为桥梁钢Q355、高碳铬轴承钢GCr15、铸态高温合金FGH96、镍基单晶高温合金DD4和锻态高温合金FGH96，样品编号及详细信息见表1。首先，选用平均粒径为177 μm的碳化硅砂纸对样品进行表面研磨，采用火花放电原子发射光谱仪(AES，ARL4460)对样品的成分进行定量分析。随后，对样品表面进行金相抛光腐蚀后，采用金相显微镜(Leica，DM6000M)对1号和2号样品进行微观组织采集，采用扫描电子显微镜(钢研纳克&聚束科技，Navigator-OPA)对3号、4号和5号样品的特征微观组织结构进行采集。采用ABAQUS有限元软件模拟2种不同硬度参量的组织结构在等静压环境下的变形情况。再将5块样品重新抛光处理，使用显微维氏硬度仪(Qness，Q10A+)在10.0 N载荷作用下测试每个样品的硬度。采用白光干涉三维轮廓仪(Bruker，Contour GT-X)分别对金相抛光后的样品表面形貌进行扫描，选用20倍干涉物镜和0.55倍目镜，获得样品初始表面的粗糙度。然后，将5块样品放入冷等静压机(CISRI，CIP500/1500-300)，以纯水作为传压介质，保持190 MPa压力0.5 h，使样品表面发生形变，取出样品后再次使用白光干涉三维轮廓仪分别对样品表面形貌进行扫描。最后，统计等静压前后样品表面的形变差异，并与样品的显微硬度值进行比对分析，探究样品表面形变与硬度间的相关性。

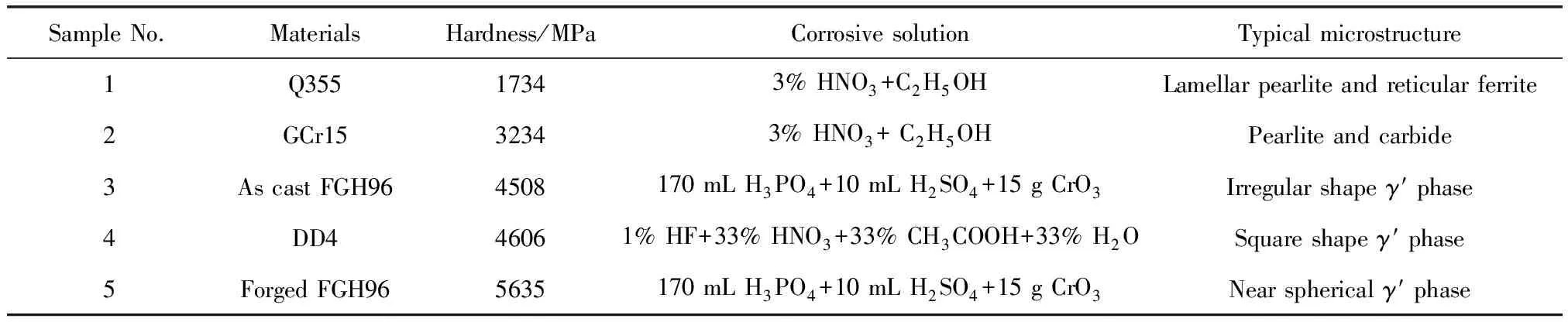
表1 实验样品信息

3 结果与讨论

3.1 成分与微观组织

由表2中样品的化学成分的光谱分析结果可知，1号样品属于铁基体的低合金钢，2号样品属于铁基体的高碳铬钢，3号、4号和5号样品均属于镍基体的高温合金。

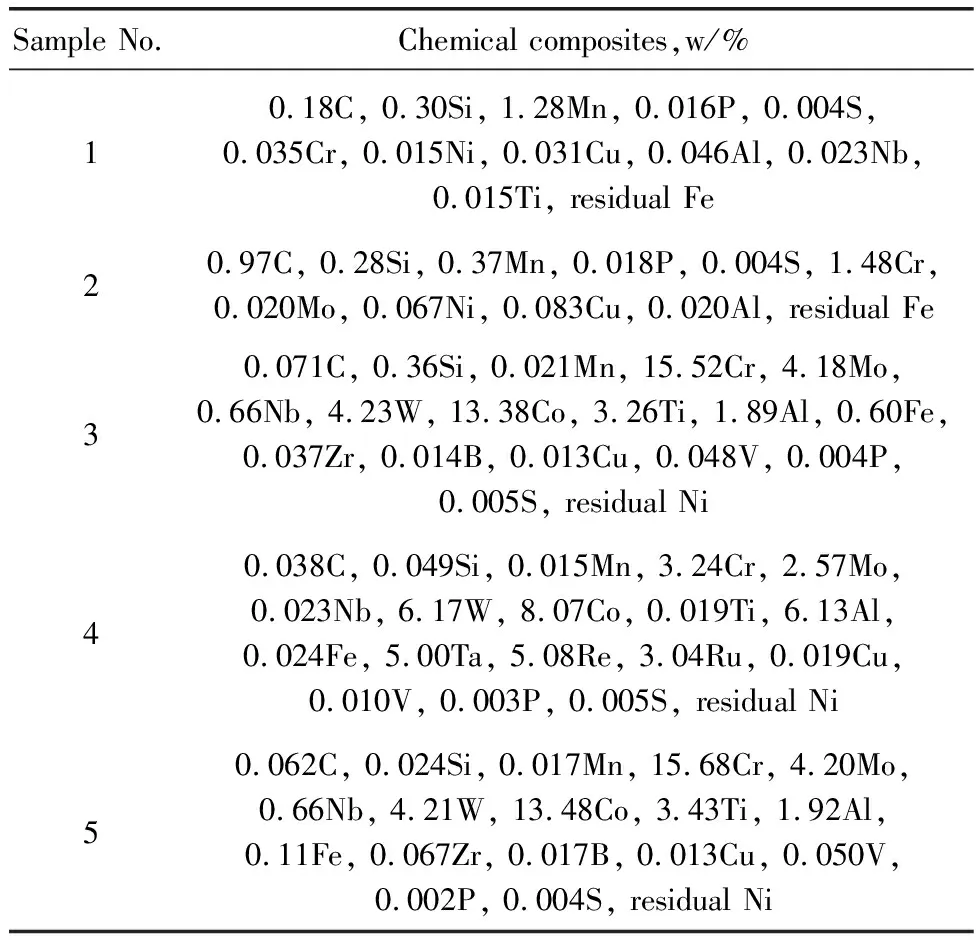
表2 实验样品化学成分

图1为5块实验样品的微观组织结构的形貌。图1a显示，1号样品的微观组织为片状珠光体和网状铁素体，由于其含碳量较低，为0.18%(质量分数，下同)，因此一般具有较低的硬度(1734 MPa)，但其强度较高、韧性较好，有良好的抗疲劳性。图1b显示，2号样品的微观组织为细小、均匀、完全球化的珠光体且伴有析出碳化物，其碳含量较高，为0.97%，因此相较于1号低合金钢具有较高的硬度(3234 MPa)和耐磨性。图1c显示，3号样品的微观组织为多种不规则形态的γ′析出相，球形、块状和蝶状的γ′相尺寸约为30～100 nm，还存在尺寸为几个微米的长条状γ′相。图1d显示，4号样品的特征微观组织为方块状γ′析出相，尺寸约为400 nm。图1e显示，5号样品的特征微观组织为近球形的γ′析出相，尺寸约为30～100 nm。镍基高温合金组织组成主要以奥氏体γ基体相和Ll2型γ′相为主，γ′相的主要组成是Ni3Al，约占高温合金的60%～70%，是最重要的沉淀强化相，也是影响高温合金力学性能的最主要因素。3号样品和5号样品同属于多晶体高温合金，存在晶界、碳化物和γ′共晶相，高温应力状态下这些区域首先容易发生损伤。由于3号样品γ′相形态不规则、分布不均匀，直接影响其力学性能，这也是3号样品比5号样品硬度值低的原因之一(见表1)。4号样品属于单晶体类型的高温合金，没有晶界，几乎消除了碳化物和共晶相，其力学性能由γ基体和γ′相决定[33]，因此其强化机理也不同于3号和5号样品。

图1 5种样品微观组织结构照片：(a)1号，(b)2号，(c)3号，(d)4号，(e)5号Fig.1 Images of the typical microstructure of five samples：(a)1#，(b)2#，(c)3#，(d)4#，(e)5#

3.2 基于有限元计算的组织变形分析

根据前面微观组织分析可知，1～5号样品均是由2种以上不同的相构成，由于每一种相的硬度和性能各不相同，导致最终组合形成的材料性能存在差异。为了分析当金属材料中基体组织与第二相之间存在较大的性能(如硬度)差异时，整体结构在高压水环境作用下的变形状态和情况，采用ABAQUS有限元通用软件，进行了几何简化模型的建立和计算，如图2所示。在简化模型中，假设结构为一个微米尺度的薄片，而薄片结构中包含了基体和4个分散分布、贯穿薄片的第二相，如图2a所示，其中符号M代表基体组织，符号P代表第二相。通过给基体和第二相赋予不同的弹性模量、屈服强度等性能参数，来区别高硬度和低硬度的相。在本模型中，设置硬相的屈服强度为800 MPa、弹性模量为228 GPa；软相的屈服强度为350 MPa、弹性模量为150 GPa。为了模拟样品在高压水介质中均匀受力的情况，在样品的6个面分别施加190 MPa的压力，设置各接触面无摩擦[34]，如图2b所示。当计算模型设置基体相为软相、第二相为硬相时，由于较软的基体组织变形量比较硬的第二相的变形量更大，从而导致在基体与第二相界面处受挤压产生较高的凸起，如图2c。反之，当计算模型设置基体相为硬相、第二相为软相时，较软的第二相会因较大的变形量而发生凹陷现象，而基体与第二相界面处不会发生明显的挤压凸起，如图2d所示。此外，还计算了其它简化的模型，改变第二相在基体中的分布方式和贯穿内嵌的方式后，分析组织形变情况，获得的变形趋势基本一致。由此可见，当对材料中硬度不同的两相组织同时施加相同压力时，两相组织都将发生形变，硬度低的组织形变量更大，而最终测量得出材料表面出现凸起和凹陷。

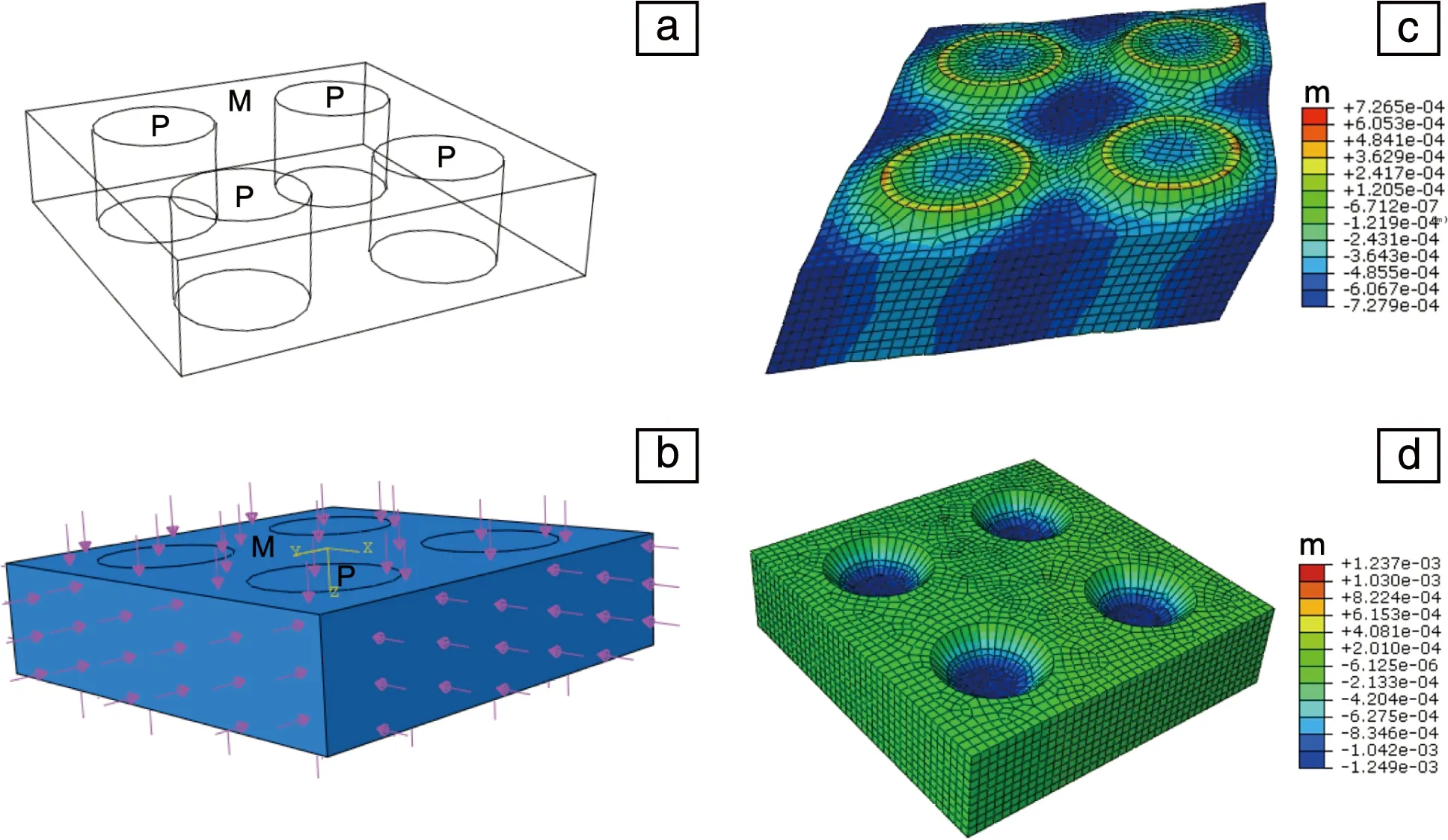
图2 组织结构在等静压下的变形模拟：(a)析出相P与基体相M的几何分布，(b)等静压时模型的外部受力设置，(c)基体为软相且析出相为硬相时模型的变形分布情况，(d)基体为硬相且析出相为软相时模型的变形分布情况Fig.2 Deformation simulation of microstructures under isostatic pressure：(a)geometric distribution of precipitated phase P and matrix phase M，(b)external pressure setting of model during isostatic pressing，(c)deformation distribution of the model when the matrix phase is soft and precipitate phase is hard，(d)deformation distribution of the model when the matrix phase is hard and precipitate phase is soft

3.3 冷等静压前后样品表面变形分析

本研究创新性地采用了白光干涉轮廓仪进行形貌采集，即3D检测领域精度最高的测量仪器之一。此方法属于非接触式测量，测试速度快，高度方向上能实现0.1 nm～10 mm全量程闭环扫描，测量分辨率达0.01 nm，使样品表面的微小形变能被精确检测。

图3为冷等静压前1～5号样品的表面形貌高度信息。由于样品经冷等静压后表面将产生亚微米至微米级的形变，因此样品表面的初始粗糙程度是影响形变量误差分辨率可信度的重要因素。将5块样品表面抛光至尽可能平滑的镜面状态，为获取每个样品中相同数量的粗糙度数据，分别在样品中心选取直径为8 mm的圆形范围，作为冷等静压前的有效分析数据。图3a～3e分别为1～5号样品冷等静压前的表面高度二维分布图，由此分布数据可知，该范围内样品表面形貌高度分布均较为平滑。图3f～3j分别为图3a～3e范围内表面形貌高度的数据集，此范围内约有4×106个高度数据，图3f～3j显示5块样品表面的平滑程度均较好。图3f和3g显示，1号和2号样品的表面高度曲线含有极少量的较高的“毛刺”，其为划痕；图3h～3i显示，3号、4号和5号样品表面的高毛刺比1号和2号样品略多。对图3f～3j中红色方框内低背景区域进行放大后显示，每个样品绝大部分区域的总高度差约10～20 nm。因为本研究是考察冷等静压前后样品表面的高度差变化，所以每个样品表面的初始平滑程度不同并不会对结果造成较大影响。

图3 冷等静压前1～5号样品表面形貌高度信息：1 号(a)、2号(b)、3号(c)、4号(d)和5号(e)样品二维分布；1 号(f)、2号(g)、3号(h)、4号(i)和5号(j)样品数据集Fig.3 Surface height information of 1#～5# sample before cold isostatic pressing(CIP)：2D surface hight distribution of sample 1# (a)，2# (b)，3# (c)，4# (d)，5# (e)；and the dataset of sample 1# (f)，2# (g)，3# (h)，4# (i)，5# (j)

图4为1～5号样品经冷等静压后的表面形貌高度信息，选取同样直径为8 mm圆形范围，白光干涉形貌分析表明，样品表面出现了许多明显的凹痕(图4a～4e)。同样，对该圆形范围内的表面形貌高度数据集进行统计，图4f～4j显示，冷等静压后样品表面发生了较大的形变，毛刺高度变化可达1 μm以上，并且5个样品的形变量有较大差异。1号样品的硬度最低，其形变量最大，高度信息最高最密；2号样品硬度稍高，其高度信息较低较密；3号、4号和5号样品随硬度增大而形变量减小，高度信息比较低且稀疏。等静压前样品表面的粗糙程度为10～20 nm，与等静压后微米级的形变量相比可忽略不计，同时也说明此抛光制备方法已满足流体微探力学性能表征研究的需求。

冷等静压后样品表面产生的形变与硬度测试所产生的压痕类似，在硬度小的样品表面的压痕更深且更大，将压头逐步缩小时依然有此规律。从宏观维氏硬度到显微维氏硬度再到纳米压痕法，人们不断缩小静载荷压头的尺寸以提高硬度测试的分辨率。本研究中的静载荷是水介质，可以被视为连续分布的“亚纳米级压头”(水分子直径0.4 nm)，这些“亚纳米级压头”呈水流体式连续分布并作用在材料的整个表面，作用力和作用过程都是均匀的，只要材料或构件能放入冷等静压缸体，就能进行全尺寸检测。为了能够定量化给出毛刺与硬度的数学相关性，对冷等静压前后的形变数据进行数理统计与解析，从而获得表面形变量与硬度的数学模型。

3.4 基于拉依达准则的数据统计解析

图5a为拉依达准则原理图，又称3σ准则曲线，是一种适用于大样本数据集中粗大误差剔除的数据处理方法。此方法先假设一组数据只含有随机误差，计算这组数据的标准偏差，然后确定一个置信区间(一般以3σ的99.7%为标准)，认为超过这个置信区间的误差属于粗大误差，即变化异常大的数据。但3σ准则仅局限于对正态或近似正态分布的大样本数据进行处理。

图5 样品表面形变量统计：(a)拉依达准则曲线，(b)样品表面形变量与硬度的相关性Fig.5 Surface deformation statistics of samples：(a)Pauta criterion，(b)correlation between surface deformation and hardness of samples

本研究中所采集的每个样品的表面形变量数据约有400万个，且符合正态分布，即符合3σ准则的要求。基于第2.2节的有限元预测模型结果，应将冷等静压后样品表面的凸起和凹陷都视为形变影响，即对应的正值和负值数据，而如何选取有效的凸起和凹陷数据就变得至关重要。分别以2.5σ和3σ置信区间选取正负阈值，在阈值以内的数据仍然符合正态分布，被视为没有发生明显形变，将正负阈值以外的数据视为粗大误差，即为样品表面产生的有效大形变量数据。实验中的标准偏差σ计算式为：

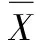
表3为5个样品在2.5σ置信区间的统计数据，表4为5个样品在3σ置信区间的统计数据。由数据可知，正负阈值以外的数据的数量远远低于数据总量，说明样品表面发生较大变形的区域较少，通过有限元模拟结果推断，这些较大变形的区域可能集中在两相交界处，数量较少。由于样品表面的凸起和凹陷都代表形变，将阈值外的表面凹陷数据(负值)取绝对值后与凸起数据(正值)加和，作为样品表面总形变量，简化讨论其与硬度的相关性。

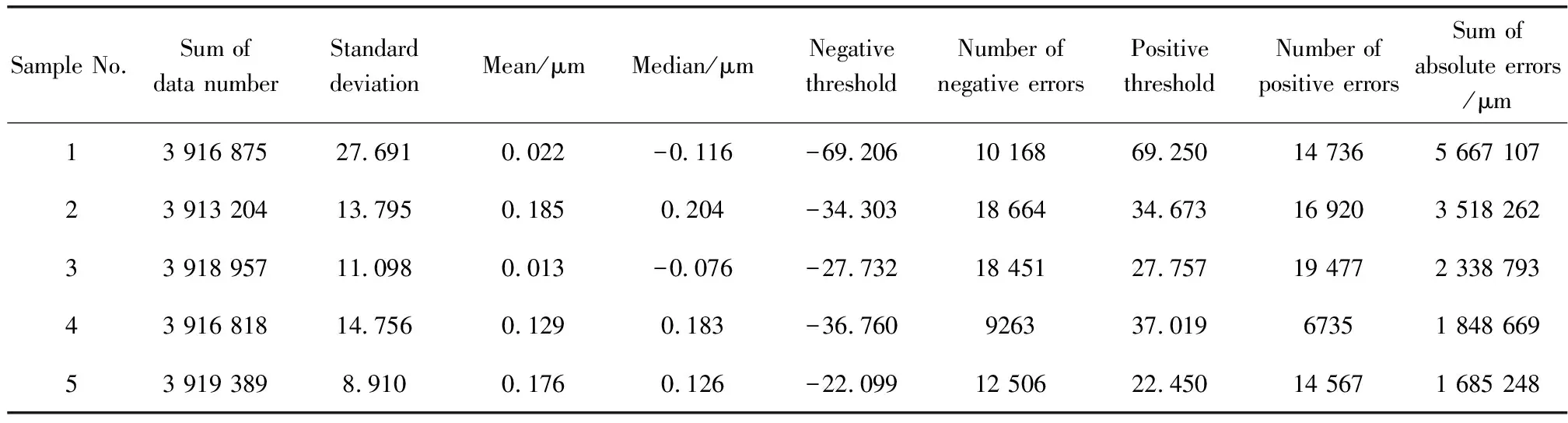
表3 1～5号样品2.5σ置信区间的统计数据

表4 1～5号样品3σ置信区间的统计数据

图5b显示，在2.5σ和3σ置信区间时阈值外数据绝对值总和与显微硬度值的相关性均较好，相关系数R2分别达到了0.99和0.9948。3号(4508 MPa)和4号(4606 MPa)样品的硬度接近，虽然微观组织具有明显差异，但取3σ置信区间时二者的线性更佳，此时检测的灵敏度更优，也说明此方法适用性广泛。因此，选择3σ置信区间作为本方法的数据统计阈值。

实验所选取的5个样品经质量检测无明显微观缩孔，可认为已经达到理论致密度，高压所引起的样品内部收缩再致密化可忽略不计。因此，近似认为形变均来自于高压水介质对样品表面压力作用的结果。实际上，当显微硬度压头作用在样品表面上时，同样也存在压头对样品内部作用力的传递。从形式上看，等静压与显微硬度加载的力的作用方式相似。

4 结 论

利用冷等静压技术开发了一种创新性的硬度性能表征方法。采用高压水流体作为载荷使材料表面产生形变，利用表面形貌仪采集样品全表面形变，通过表面形变大数据的统计解析，建立了样品表面形变与硬度的相关性数学模型，并且通过有限元建模，预测了不同硬度的两相组织在等静压条件下的变形行为，验证了不同类型金属材料的表面形变与硬度均具有非常高的相关性。该表征方法分辨率可以达到纳米级，可视为硬度的无损检测方法，能够实现从纳米到厘米(甚至米级)真正连续跨尺度塑性形变表征。