深度学习神经网络ぴ诨鸬绯Х门故障诊断与预警中的应用

周传杰 王嘉琪 马运保 杜伟

摘 要：针对燃煤发电机组的重要执行机构阀门，通过深度神经网络算法对机组大量运行数据进行学习，构建重要执行机构阀门在全负荷工况下的精准数学模型，以深度神经网络模型预测值和皮尔逊相关系数判别为依据，实现重要执行机构阀门的故障诊断和早期预警。结果表明，基于大数据，学习和深度神经网络算法的数学模型有效地实现了对执行机构阀门的故障诊断和提前预警，指导运行人员进行提前干预和检修，减少机组的故障率。执行机构阀门故障预警的深度神经网络模型以执行机构阀门前的相关DCS参数、系统主要运行参数作为模型的输入变量；以执行机构阀门之后的参数作为输出量。选择机组在不同负荷工况下，执行机构阀门系统从打开到关闭的完整时间段内的大量数据，作为深度神经网络模型的训练数据。该方法具有较强的通用性，可以方便地平行移植至火电机组的其他重要辅机设备中。皮尔逊相关系数能反映数据变化的趋势信息，能判断两个向量或者两个数组相似度。以皮尔逊相关系数作为深度神经网络模型预测输出值与系统实际输出偏差距离的判据，可以很好地解决系统发生偏离后的预警问题，有效地提高模型预测的精度。

关键词：深度神经网络算法；皮尔逊相关系数；执行机构阀门故障预警；多维度距离偏差监测；大数据分析

在能源转型的背景下，智能发电成为发电行业转型升级的新兴技术［13］。智能发电从智能生产控制和智能管理两个核心展开，借助智能控制、智能安全、智能管理三大功能，综合自学习、自恢复、自适应、自诊断等技术，形成了一种智能发电运行控制和管理模式［25］。这种模式具备自驱优化全程控制、自学习分析诊断、自恢复故障处理、自适应多目标优化和自组织细致管理等特征。

在故障诊断方法研究中，文献［38］中将故障诊断方法分为基于模型的故障诊断、基于信号的故障诊断和基于历史运行数据的故障诊断这三大类。

基于模型的故障诊断方法首先需建立系统的精准数学模型，通过模型参数的变化实现对系统的监测，因此所建立的模型是否准确将直接决定预警及诊断结果的可靠性。基于信号的故障诊断方法通过对关键检测信号进行小波分析，以及通过对信号的频域和幅值相关性分析对机组是否具有潜在故障进行诊断，但其需安装大量的传感设备，实施和维护成本较高。基于历史运行数据的故障诊断方法，通过分析机组正常运行数据与故障运行数据的差异，判断系统是否处于异常状态。基于历史运行数据的故障诊断方法需获取系统的大量典型故障历史数据样本，而在电厂的海量历史数据中寻找故障数据如同海底捞针，且故障数据非常有限，因此在实际中难以实施。

在燃煤火电厂系统中，执行机构阀门是常见的一种设备，它主要起到对流体进行控制的作用。现代化的燃煤火电厂中含有大量的阀门，阀门在其中起着控制介质输送的作用，是保证火力发电厂正常运转的重要环节。在火力发电厂的热工系统中，执行器是非常普遍的一种设备。现代燃煤火力发电厂中，在正常运行的情况下，阀门的开关频率较高，极易引起阀门的性能劣化，引起安全事故。在火力发电厂发生的各种事故中，由于阀门的原因引起的事故占到了70%左右，因此，阀门的工作可靠与否直接关系到火力发电厂的安全运行。所以，本文将以执行机构阀门为研究对象，采用深度神经网络算法对执行机构阀门系统海量历史数据进行学习，构建执行机构阀门系统在各种工况下的精准数学模型，从而建立出了执行机构阀门系统在不同工况下的精确数学模型。

以深度神经网络模型预测值和皮尔逊相关系数判别为依据，开发出一套故障诊断与预警系统，实现执行机构阀门的故障诊断和早期预警。通过实例验证，本文所提出的方法可以对电动阀门的工作状况进行正确的判别，可以对阀门的内漏度做出较为精确的判别；并在系统的测试中，证明了该系统的模块功能是有效的。本文探讨的重点是探讨自学习、自分析和自诊断等新技术，并将新技术应用于燃煤机组重要执行机构阀门的故障诊断和预警，提高了火电机组运行的安全可靠性，推动电厂向智能生产控制与管理升级［912］。

1 数据预处理

1.1 历史数据抽取和预处理

在实际应用中，主要从质量分析、数据转换、再取样等几个方面来进行预处理：

（1）数据质量分析是指检测数据缺失值和异常值情况，并加以处理，以提升数据质量，使数据适合某一种特定的挖掘技术与工具。缺失值处理方法有：自动删除不符合要求的记錄、均值/中位数/众数插补、固定值插补、回归方法插补、不处理等；异常值处理方法有：异常值删除、视为缺失值、不处理等；数据噪声处理可采用参数平滑相关算法。

（2）数据变换主要是为了对数据进行规范化处理，以供挖掘。转换方法有：简单函数变换、正态分布变换、非平稳到平稳序列的变换和量程压缩；数据规范化（归一化）包括最小—最大规范化、零—均值规范化和小数定标规范化等。

（3）数据重取样是指为了去除一些噪声，适应建模算法的要求，减少数据量，加快建模速度，对数据进行再取样，并在前一个取样周期的整数倍上对数据进行再取样处理，从而去除一些噪声，适应建模算法的要求［8］。在此基础上，本文采用了一种基于前一周期的整数倍采样方法，以消除部分噪声，并使其与模型的需求相匹配，以降低模型的样本数量，提高模型的速度。

1.2 历史数据筛选和挖掘

火电机组锅炉系统运行优化所需测点均是时序信号，操作人员的运行优化控制对系统的影响可转化为数据相关性模型。

基于锅炉运行优化的特点，本发明提出了针对对象相关性的数据挖掘技术：

（1）初态稳定性抽取：选取处于稳态转化为动态的数据片段，以用于多变量线性离散状态空间相关性分析；

（2）根据具体情况进行筛选：如工况筛选、动态数据筛选等。

如图1所示是用于数据预处理和挖掘的人机交互平台界面。

2 深度神经网络算法和皮尔逊相关系数

2.1 深度神经网络算法

深度前向全连接神经网络（Deep Neural Networks，DNN）本质上是一个包含多个隐层，结构深度多层化的多层感知机［37］。图2是一个包含五个隐层的，每层含有若干个节点的深度神经结构示意图。深度神经网络（DNN）采用层级的结构，每层之间相互连接，包括输入层、隐藏层和输出层。相邻层的节点往往采用全连接的方式，因为全连接的深度神经网络往往会出现过拟合的情况。一般会构造稀疏深度神经网络，以降低过拟合度，断开某些层之间点与点的连接。隐藏层的节点激活值是由前一层神经网络的激活值和当前层神经网络权重的线性加权求和，并加上偏置后，最终通过非线性的激活函数激活得到。

DNN的输入层输入预处理之后的数据，设输入为h0=X，对于有L层隐含层的深度神经网络，其每层的激活值的计算公式为：

α（l）=W（l）h（l－1）+b（l），（1SymbolcB@

lSymbolcB@

L+1）

h（l）=f（α（l）），（1SymbolcB@

lSymbolcB@

L）（1）

式中，Wl为l-1到l层的权重向量，hl-1为l-1层隐含层的激活值，bl为偏置向量，hl为l层的激活输出。f（·）为激活函数，传统的DNN普遍采用Sigmoid激活函数，其函数表达式为：

h（l）=f（α（l））with hlj=11+e－alj（2）

目前，新兴的激活函数为整流线性单元（Rectified Linear Unit，ReLU），常用于隐藏层节点的非线性激活函数。其表达式为h（l）=max（0，al）。ReLU因其求导简单，使用ReLU训练时的收敛速度比较快，也不会出现梯度消失的问题。相对于Sigmoid函数，ReLU具有单侧抑制、相对宽阔的兴奋边界和稀疏激活性等优点。

对于回归拟合的任务，DNN的輸出层通常采用Sigmoid激活输出。当使用DNN接受输入层的数据，并相应计算出输出层的数据的过程，称为前向传播过程（Forward Propagation）。当得到DNN输出的理论计算值与实际数据值进行比对时，需建立相应的损失函数。根据不同的任务，DNN常用有两种优化准则。对于分类任务，通常使用交叉熵准则，对于回归任务（CrossEntropy，CE），通常使用最小均方差（Mean Square Error，MSE）。最小均方差的损失函数公式为：

J（Θ）=12N∑N1‖yl－hl‖2（3）

式中，Θ={Wl，bl|l=1，2，…，L+1}表示DNN中的所有参数，yl为输出的实际值。DNN的反向传播，学习训练任务是使损失函数的值达到最小，达到最终的回归优化拟合效果，即：

Θ*=minΘ∈瘙 綆

NJ（Θ）（4）

对于有多个隐藏层、多个节点的深度神经网络，上述的优化过程通常是高维、非凸的。反向传播过程可采用基于随机梯度下降（SGD）的BP算法来进行优化。反向传播算法（BP算法）的训练过程，其核心思想是通过链式求导方法，计算出目标函数关于每层的输出误差，进一步得到网络参数的梯度，进而来调整每个网络节点的参数值。通过链式求导法则得到对应的误差信号表达式为：

elγ=ylγalγ（5）

得到第l层输出的误差信号后，权重的梯度通过误差信号可计算得到：

JWl=elγ（hl－1γ）′（6）

权重更新公式为：

ΔWlt+1=ρ·ΔWlt－（1－ρ）·ηJWlt

Wlt+1=Wlt－ΔWlt+1（7）

式中，ρ为动量因子，η为学习速率。

为了有效地防止参数更新过程中，出现太大的权值，在目标函数中添加权重，相应的权重更新公式为：

ΔWlt+1=ρ·ΔWlt－（1－ρ）·η（JWlt+βWlt）（8）

式中，β为权重衰减因子，通常取为0.001。

2.2 皮尔逊相关系数

采样点间距是衡量两条曲线相似性的重要指标，然而对具有规律性的燃煤发电系统，仅靠间距难以体现出各参数之间的时间相关性，即曲线变化的趋势信息未被充分表达。皮尔逊积矩相关系数（Pearson ProductMoment Correlation Coefficient，又称作PCCs或PPMCC，简称为皮尔逊相关系数）是一种常用的数值分析方法，用于衡量X、Y两个变量间的线性相似度，其值在（-1，1）的区间内，取1代表完全的正相关性，而取-1则代表完全的负相关性。

X和Y之间皮尔逊相关系数的计算公式为：

ρx，y=cov（X，Y）σXσY

=E（（X－μX）（Y－μY））σXσY

=E（XY）－E（X）（Y）E（X2）－E2（X）E（Y2）－E2（Y）（9）

式中，E代表数学期望值。

皮尔逊相关系数ρx，y应满足如下性质：

（1）若ρx，y=±1，当且仅当Y=aX+b，a≠0，a，b为常数；

（2）ρx，y∈（－1，1）；

（3）cos0°=1。

式（9）出示皮尔逊相关系数ρx，y的计算方法，即将X和Y的协方差cov（X，Y）与它们的标准差乘积σXσY相除。通过几何学的方法，可以更好地了解相关性的意义。皮尔逊的相关系数，可以看成是两个矢量之间的角度，用来计算余弦。当向量夹角为0°，即两者向同一方向变化时，cos0°=1，即ρX，Y=1 ρx，y=1，表明二者此时共变，较大程度上反映了数据变化的趋势。

与欧几里得距离相比，皮尔逊相关系数能够更有效地表示复杂的数据信息，并判断两个向量或数组的相似度。在数据不规范的情况下，它往往能够给出更好的结果。对于本研究对象，与只选择单一参数点作为故障样本相比，该模型的预测精度将大大提高。虽然模型预测的结果与实际数据并不能完全吻合，但是当数据存在一定差异但总体趋势相近时，可以给出较高概率的输出结果，并以此作为故障产生的依据。

皮尔逊相关系数g=cov（X，Y）/（aX*aY），表示两个向量的夹角余弦值。如果向量夹角为0度，则c=1，b=1，说明它们共变，并反映出数据变化的趋势。皮尔逊相关系数可以比欧几里得距离更好地表示数据信息相似度，尤其适用于不规范的数据。对于本研究模型，通过建模获得的数据变化趋势，预测结果的准确性将显著提高。即使数据存在一定差异，但整体趋势类似，模型能够提供相对高的概率输出结果，作为故障判断的支持依据。

3 执行机构阀门故障预警仿真验证

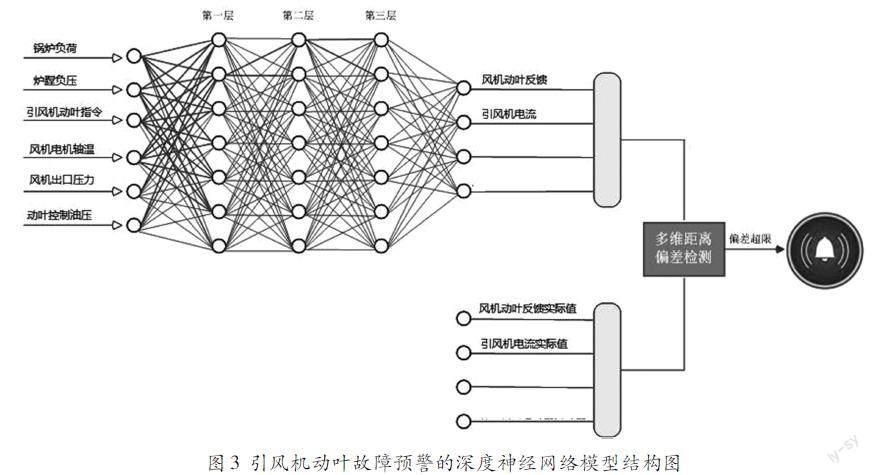
以引风机动叶故障为例，利用深度神经网络算法，对引风机动叶执行机构进行建模。以引风机电流、炉膛负压、锅炉负荷、风机出口压力、风机动叶液压油压力作为模型的输入变量，以引风机动叶的反馈作为输出量，选择机组在不同负荷工况下，输入输出量的海量数据，作为训练数据。针对风机动叶故障预警的深度神经网络算法的系统结构如图3所示。

选择半个月的海量历史运行数据，选取深度神经网络隐含层为3层，每层节点数分别为30、50、30，权重更新速率为1，模型训练代数为100代。引风机动叶故障预警的深度神经网络模型的验证效果如图4所示。图3显示出引风机动叶反馈预测值与实际值的曲线基本吻合，平均相对误差小于5%，满足模型精度的要求。说明基于大数据学习和深度神经网络，构建的引风机动叶系统数学模型，能有效实现引风机动叶系统的参数预测。

截取某时间段内，引风机动叶运行数据作为测试样本，对执行机构故障诊断和预警系统进行验证。如图5所示。当时间达到1286s时，模型预测输出值与实际值之间的皮尔逊相关系数小于0.6，并以此进行故障预警。28s后，實际动叶发生卡涩，实现了对执行机构系统故障的提前预警。

4 结论

针对燃煤火力发电站的执行机构阀门，采用深度神经网络算法对执行机构阀门系统海量历史数据进行学习，构建执行机构阀门系统在全负荷工况下的精准数学模型，以深度神经网络模型预测值和皮尔逊相关系数判别为依据，实现执行机构阀门系统的故障诊断和早期预警。结果表明：

（1）执行机构阀门故障预警的深度神经网络模型以锅炉负荷、炉膛负压、动叶指令、风机轴温、风机出口压力、控制油压作为模型的输入变量；以风机动叶反馈、引风机电流作为输出量。选择机组在不同负荷工况下，引风机系统从启动到停止的完整时间段内的海量数据，作为深度神经网络模型的训练数据。

（2）基于深度神经网络构建的执行机构阀门系统数学模型，能有效实现执行机构阀门的故障诊断和早期预警。该方法具有较强的通用性，可以方便地平行移植至火电机组的其他重要辅机系统中。

（3）皮尔逊相关系数能反映数据变化的趋势信息，能判断两个向量或者两个数组相似度。以皮尔逊相关系数作为深度神经网络模型预测输出值与系统实际输出偏差距离的判据，可以很好地解决系统发生偏离后的预警问题，有效地提高模型预测的精度。

参考文献：

［1］李孟周，伏劲宇，杜杰，等.燃煤火电集控运行精益化管理提升策略研究［J］.电力设备，2017（34）：230，232.

［2］国家能源局.关于推进“互联网+”智慧能源发展的指导意见［EB/OL］.［20160229］.

［3］刘吉臻，胡勇，曾德良，等.智能发电厂的架构及特征［J］.中国电机工程学报，2017，37（22）：64636470.

［4］高波，李宁，孙奇辉，等.燃煤电站执行机构阀门出力不足的系统分析与优化［J］.科研，2016，5（9）：4243.

［5］Agrawal V，Panigrahi B K，Subbarao P M V.Review of control and fault diagnosis methods applied to coal mills［J］.Journal of Process Control，2015，32：138153.

［6］王金浩，陈伟巍，陈铮，等.1000MW机组输煤控制系统通讯网络升级优化改造［J］.防护工程，2018（2）：293294.

［7］刘瑞国.一个基于模型的故障诊断算法［J］.微计算机信息，2007，23（13）：219221.

［8］杨利，邹成，胡建忠，等.中速辊式执行机构阀门单耗的分析与运行优化［J］.工业，2016，10（9）：5152.

［9］文成林，吕菲亚，包哲静，等.基于数据驱动的微小故障诊断方法综述［J］.自动化学报，2016，42（9）：12851299.

［10］吴英.基于证据理论的民机电源系统故障诊断方法［J］.国外电子测量技术，2017，36（8）：510.

［11］Heaton J.Ian Goodfellow，Yoshua Bengio，Aaron Courville.Deep learning［J］.Genetic Programming & Evolvable Machines，2017，19（12）：13.

［12］刘畅.电站设备辅机状态监测与故障诊断［D］.华北电力大学（北京），2017.

作者简介：周传杰（1973— ），男，本科，工程师，主要从事热工保护及自动化；王嘉琪（1994— ），女，研究生，工程师，主要从事热工保护及自动化；马运保（1969— ），男，专科，工程师，主要从事热工保护及自动化。