基于正交设计的旋流管式除雾器性能的数值分析

刘定平 张向阳 陈爱桦 王海 何文浩

（华南理工大学 电力学院/广东省能源高效清洁利用重点实验室，广东 广州 510640）

目前，湿法脱硫大约占国内烟气脱硫技术的93%［1］，除雾器是湿法脱硫系统的末端用于去除经湿法脱硫后的烟气中夹带液滴的装置，是湿法脱硫系统中的重要设备。除雾器效率降低会直接导致排气中携带大量液滴，进而形成“石膏雨”。近年来随着国家对火电厂排放的要求越来越严格，对环境问题越来越重视，传统的除雾器已经不能满足越来越严格的排放标准［2-3］。因此，如何提高除雾器的性能，尤其是微细雾滴去除效率的提升是亟待解决的难题［4］。

折流板式除雾器对直径大于20 µm的雾滴有着较好的去除效果，是目前应用最广泛的除雾器。对于折流板除雾器的优化，许多学者通过加装扰动元件如添加钩片和多孔板［5-9］、优化折流板的结构来提升除雾效率［10-12］，但是对直径小于20 µm的微细雾滴去除效率仍不够理想［13］，对直径7.5～22.5 µm的雾滴去除效率只有30%左右［14］。在去除微细雾滴方面，有许多学者对声波凝并除雾［15-17］和旋流板式除雾器进行了研究［18-23］，基于离心作用的旋流板式除雾器较折流板式除雾器略有提升，但是阻力大，能耗较高。

近年来对除雾器的研究主要为实验研究和数值模拟研究，数值模拟具有节省人力、物力、时间的突出优势。通常除雾器中液滴的质量流量很低，因此可以采用欧拉-拉格朗日方法，假设气流携带液滴，但液滴对气流的影响可忽略不计，许多学者［12，24-26］采用欧拉-拉格朗日方法对除雾器内烟气流动进行数值模拟。Rafee等［12］研究发现增强壁面函数对小液滴的去除效率预测更加准确；Wang等［27］研究发现低雷诺数k-ε湍流模型比标准k-ε湍流模型的模拟结果更准确；使用随机游走模型DRW对液滴运动修正能够更加准确地预测微细雾滴的运动轨迹［13］。

综上所述，本研究针对折流板除雾器对直径小于20 µm的微细雾滴去除效率低的问题，提出一种新型的旋流管式除雾器，采用欧拉-拉格朗日的方法对旋流管式除雾器内烟气的流动进行数值模拟，并采用正交设计模拟实验研究了旋流管式除雾器结构参数对性能的影响。

1 物理模型

本研究根据脱硫塔的常见工程尺寸，设计一种新型旋流管式除雾器。其物理模型及尺寸如图1和表1所示，该除雾器由入口段、捕集段以及出口段组成，捕集段由4根相同直径的圆管弯曲组合构成。其中，a为单根圆管沿中心轴从入口面至出口面的扭转角度，L1、L2分别为入口段和出口段的长度，H为捕集段的长度，D为除雾器的直径，d为单根圆管的直径，x为除雾器圆心到圆管圆心的距离，忽略管壁厚。

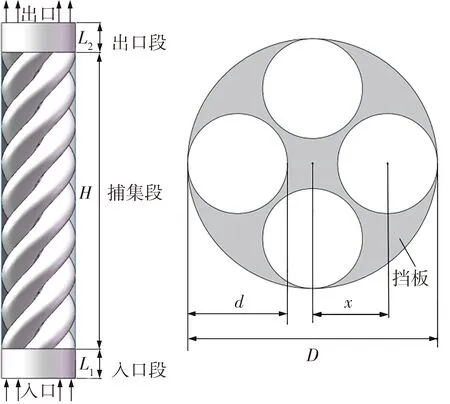
图1 旋流管式除雾器物理模型Fig.1 Physical model of cyclone tube demister

2 数学模型

2.1 模型假设

本研究采用欧拉-拉格朗日法对烟气在旋流管式除雾器内的流动进行数值模拟，结合数值模拟的特点，对模型的假设如下：

（1） 考虑到在理想情况下气体流动参数不随着时间变化发生改变，视为定常流动；

（2） 由于雾滴直径范围为2～80 µm，可以视为质量均匀的刚性硬球，并且将酸性雾滴用水滴替代计算；

（3） 不考虑雾滴之间和雾滴与壁面的相互作用力，仅考虑重力和Saffman升力［28］；

（4） 雾滴碰撞到壁面则被捕集，通过出口则逃逸。

2.2 控制方程

2.2.1 除雾器内的气体流动控制方程

对于任意流体的流动，都符合连续性方程和NS方程：

其中：V为除雾器内气体的速度矢量，F为除雾器内气体所受的质量力矢量，t为时间，ρ为流体的密度，p为流体的静压力，μ为气体的动力黏度。

对N-S方程时均化，得到湍流Reynolds应力输运方程，采用k-ε双方程模型对湍流Reynolds应力输运方程封闭。湍流脉动动能k方程和湍流脉动动能耗散率ε方程为

其中：k为湍流脉动动能；ε为湍流能量耗散率，u和x分别为速度矢量和位置矢量，下标i、j、k为哑标，符合爱因斯坦求和约定，μt为湍流粘性数，c1=1.44，c2=1.92，σk和σε分别取经验值1.0和1.3，为对应于k和ε的湍流Prandtl数。

2.2.2 除雾器内离散相控制方程

在拉格朗日坐标系下离散相的运动方程如下：

其中：u和up分别为气体和颗粒的速度；Re为相对雷诺数；dp为颗粒直径；CD为颗粒曳力系数；ρ和ρp分别为气体和颗粒的密度；gx为重力加速度；Fx为颗粒受到的附加力，由于ρp/ρ＞＞1，仅考虑Saffman升力［28］。

2.3 计算方法与边界条件

本研究采用Simple算法求解速度与压力耦合方程组；对动量方程、k方程和ε方程均采用二阶迎风格式离散；采用双向耦合计算连续相和离散相。

对连续相的设置如下：采用RNGk-ε模型对烟气的流动进行模拟；采用密度为1.225 kg/m3，动力黏度为1.789×10-5kg/（m·s）的空气替代；烟气采用速度进口边界条件，进口速度范围设置为3～7 m/s，垂直于烟道入口进入，烟气出口处采用压力出口边界条件，表压为0 Pa。

对离散相的设置如下：采用离散相模型DPM计算雾滴的运动；采用密度为998.2 kg/m3的水滴代替雾滴进行计算，同时假设液滴喷出的流速与连续相相同；液滴的质量流量Q=0.150 8UA，U为流速（m/s），A为入口处面积（m2）；喷出雾滴的尺寸分布采用Rosin-Rammler分布，直径范围为2～80 µm，平均直径为39.35 µm，分布系数为2.8；采用随机游走模型DRW对液滴运动进行修正。

2.4 性能评价指标

对除雾器性能评价的指标为除雾效率和进出口压降。进出口压降为除雾器出口与除雾器进口处静压差；除雾器的除雾效率η计算公式如下：

其中，Qin和Qout分别为进口和出口雾滴的质量流量，kg/s。

2.5 模型验证

由于本研究对象旋流管式除雾器结构为新型结构，暂无对此的实验研究，因此采用流动非常接近的旋风分离器实验对模型进行验证［29］，采用文献中的旋风分离器相同的几何模型进行数值模拟，从压降以及除雾效率进行对比验证。

数值模拟结果和实验结果对比如图2所示。从图中可以很明显地看出，压降模拟结果与实验结果非常吻合，最大的相对误差仅为6.04%；对于除雾效率，当粒径大小小于3 µm时相对误差比较小；当粒径大小大于4 µm时实验结果整体上看高于模拟结果的除雾效率。这是因为模拟时只将旋风分离器底部沉降面设置为捕集面，而实验所采用的雾滴为矿物油，可被旋风分离器内全部面捕集。总体上看，模拟结果与实验结果吻合，说明所用数学模型是适用的。

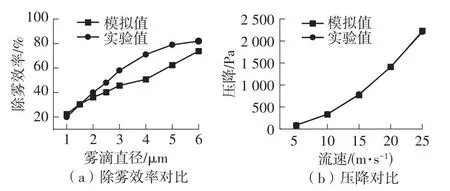
图2 数值模拟结果与实验结果对比Fig.2 Comparison between numerical simulation results and experimental results

2.6 网格独立性验证

本研究采用Fluent Meshing的多面体网格对模型进行网格划分。选取网格数69万、88万、115万、146万和178万进行网格独立性检验，结果如图3所示。从图中可以明显看出，网格数量从69万增加至178万时，除雾效率的计算结果几乎不发生改变，最大相对误差仅为0.27%；压降则先增加再下降，并在网格数为115万开始趋于平缓，最大相对下降幅度为0.08%。综合考虑计算效率以及精度，本研究的各个模型最终选用网格数为115万的网格划分方案进行划分。

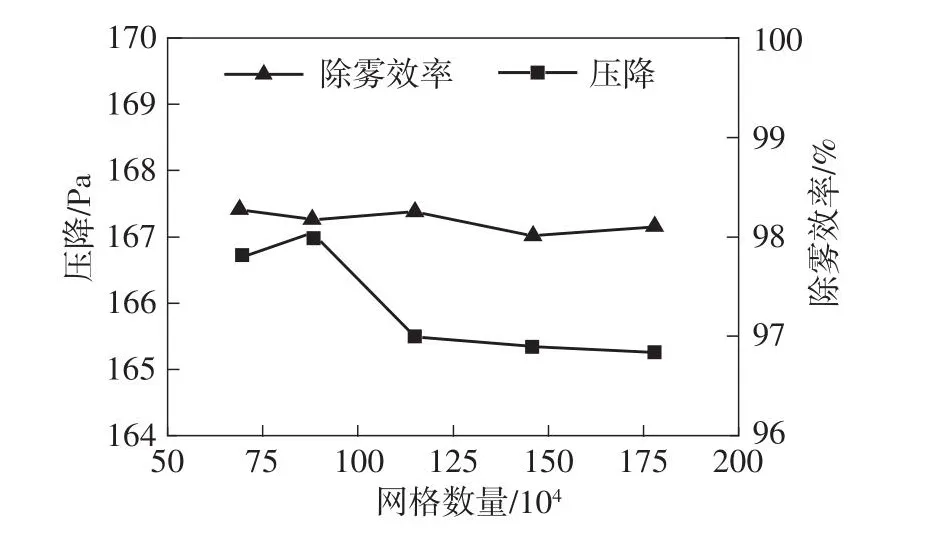
图3 网格独立性检验Fig.3 Grid independence test

3 模型计算与分析

通过设置入口流速3、4、5、6、7 m/s，分别对基础型旋流管式除雾器的性能进行分析。按雾滴直径大小分为5组（2～10、10～20、20～30、30～50、50～80 µm）进行除雾效率分析。

图4示出了不同流速下旋流管式除雾器性能的变化。从图中可以看出，随着流速的增加，除雾器的除雾效率和压降也在增加。流速为3～7 m/s时，压降从61.4 Pa上升至321.3 Pa，总除雾效率从96.8%上升至98.8%，对直径在20～80 µm的雾滴去除效率达到99.99%以上，对直径在10～20 µm的雾滴去除效率从86.5%上升至95.5%，对直径在2～10 µm的雾滴去除效率从51.3%上升至52.4%。由于直径较大的液滴所受惯性力较大，在旋流管式除雾器的结构离心作用下可以得到很好的去除效果，旋流管式除雾器对大于20 µm的雾滴去除效率高的同时，显著提升了2～20 µm的雾滴的去除效率，并且除雾器的压降也在较低水平，符合实际工程应用。

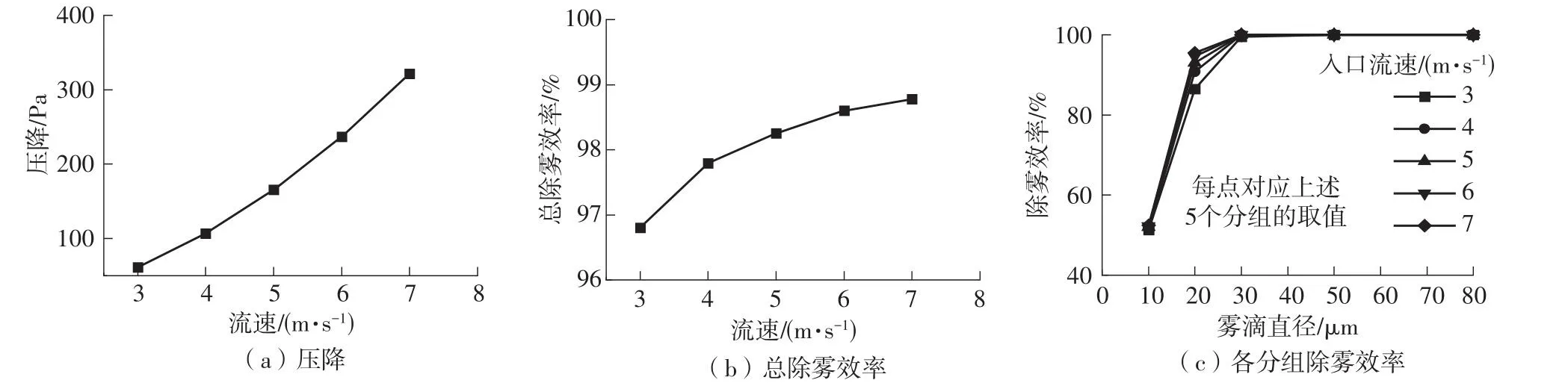
图4 不同流速对除雾器性能的影响Fig.4 Effect of different velocity on performance of demister

由于各流速下旋流管式除雾器对直径大于20 µm的雾滴去除效率可达到99%以上，因此接下来对旋流管式除雾器的性能研究基于除雾器的压降以及直径范围在2～20 µm内的雾滴的去除效率。图5示出了不同流速下直径为2～20 µm的去除效率。可以看到，随着流速的增加，对直径2～10 µm的雾滴去除效率略微上升，流速从3 m/s增加至7 m/s时上升2.2%；相比之下，流速增加对直径10～20 µm的雾滴去除效率影响较为明显，流速从3 m/s增加至7 m/s时其去除效率上升10.4%。Stokes数是描述悬浮颗粒在流体中行为的无量纲常数。当流体绕过障碍物时，若St＞1，颗粒仍按直线行驶撞上障碍；若St＜1，颗粒会紧随着流体流动。St数具体表达式如下：

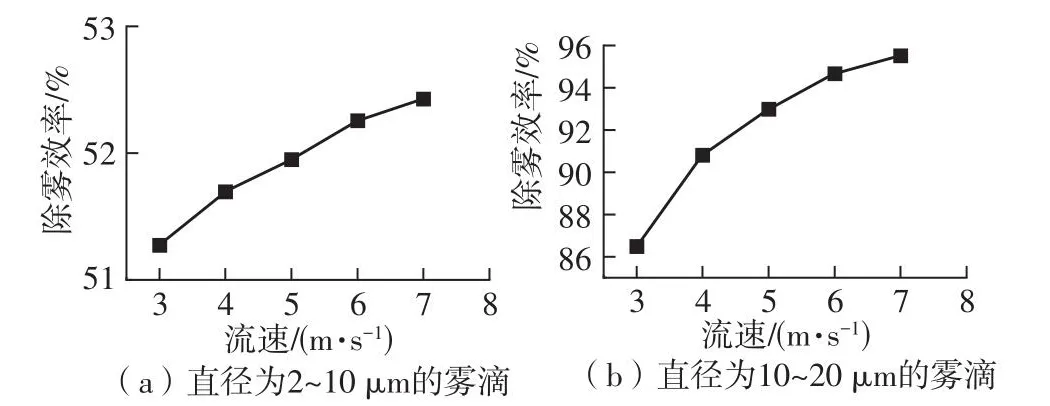
图5 不同流速对2～20 µm雾滴除雾效率的影响Fig.5 Effect of different flow rates on demisting efficiency of 2～20 µm droplets

其中：τ为颗粒弛豫时间，uo是连续相流过障碍物的流速，δc是障碍物的特征量。

流速越大，St数也越大，因此能够获得更高的除雾效率；因为微细雾滴的Stokes数比较小，所受惯性力小，随流性较好，因此流速对微细雾滴的去除效率影响不大。微细雾滴在旋流管式除雾器内随着烟气的流动转向增大与壁面碰撞概率，因此能够得到对微细雾滴更高的去除效率。

4 旋流管式除雾器性能的正交分析

4.1 正交设计模拟实验及结果

在多次模拟对比中发现，单管直径d、捕集段长度H、扭转角度a都对除雾器性能产生了影响，因此本研究选取单管直径d、捕集段长度H、扭转角度a作为影响因素，以直径2～10 µm、10～20 µm雾滴的去除效率以及压降作为响应值进行正交设计分析，并设置空白列Ω作为随机误差，采用4因素5水平的正交表，共计25组模拟工况，实验组的参数及响应值如表2所示。

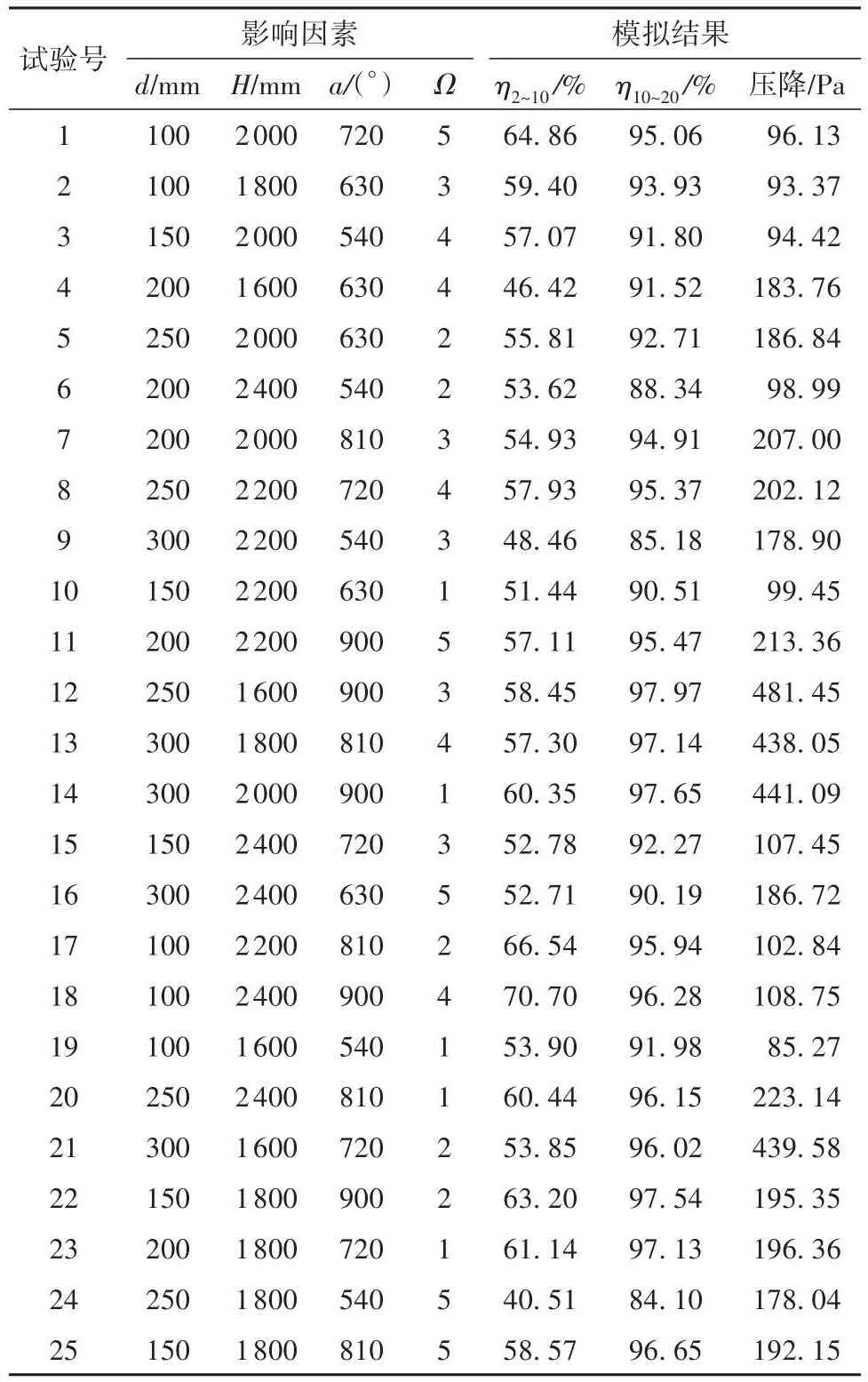
表2 正交实验表与模拟结果Table 2 Orthogonal experiment table and simulation results

4.2 以除雾效率为响应值的极差分析

4.2.1 以2～10 µm颗粒去除效率为响应值的极差分析

以2～10 µm雾滴去除效率为响应值的极差分析结果如表3所示，其中评价参数κ1为某因素在1水平下的响应值之和，而评价参数z1为某因素在1水平下评价参数κ1的均值，其余下标以此类推。极差R为评价参数z的最大值与最小值之差，用以表达因素的影响，极差越大则因素的影响越大。

根据表3最后一行的排秩表明，不同因素在这5种取值范围内，对除雾器内2～10 µm雾滴去除效率的影响从大到小为：a、d、H。结果表明：a为影响2～10 µm雾滴去除效率的主导因素，同时误差列极差较小，因此可认为各因素之间不存在交互效应。同时根据z的大小可以发现，在参数范围内，2～10 µm雾滴去除效率均随着a的增大、d的减小而增大。这是因为尽管微细雾滴随流性好，随着a的增大和d的减小，烟气在除雾器内流动转向加剧，加强了烟气流动的扰动，提高了微细雾滴与壁面碰撞的概率，雾滴在除雾器内与壁面碰撞加剧，提高了对微细雾滴的去除效率。该正交模拟试验中的最优组合为：d=100 mm，H=2 000 mm，a=900°，此时对除雾器内2～10 µm雾滴的去除效率可达到最大。

4.2.2 以10～20 µm颗粒去除效率为响应值的极差分析

以10～20 µm雾滴去除效率为响应值的极差分析结果如表4所示。表4最后一行的排秩表明，不同因素在这5种取值范围内，对除雾器内10～20 µm雾滴去除效率的影响从大到小为：a、H、d。结果表明：a为影响10～20 µm雾滴去除效率的主导因素。同时根据z的大小可以发现，在参数范围内，10～20 µm雾滴去除效率均随着a的增大、d的减小而增大。该正交模拟试验中的最优组合为：d=100 mm，H=1 600 mm，a=900°，此时对除雾器内10～20 µm雾滴去除效率可达到最大。

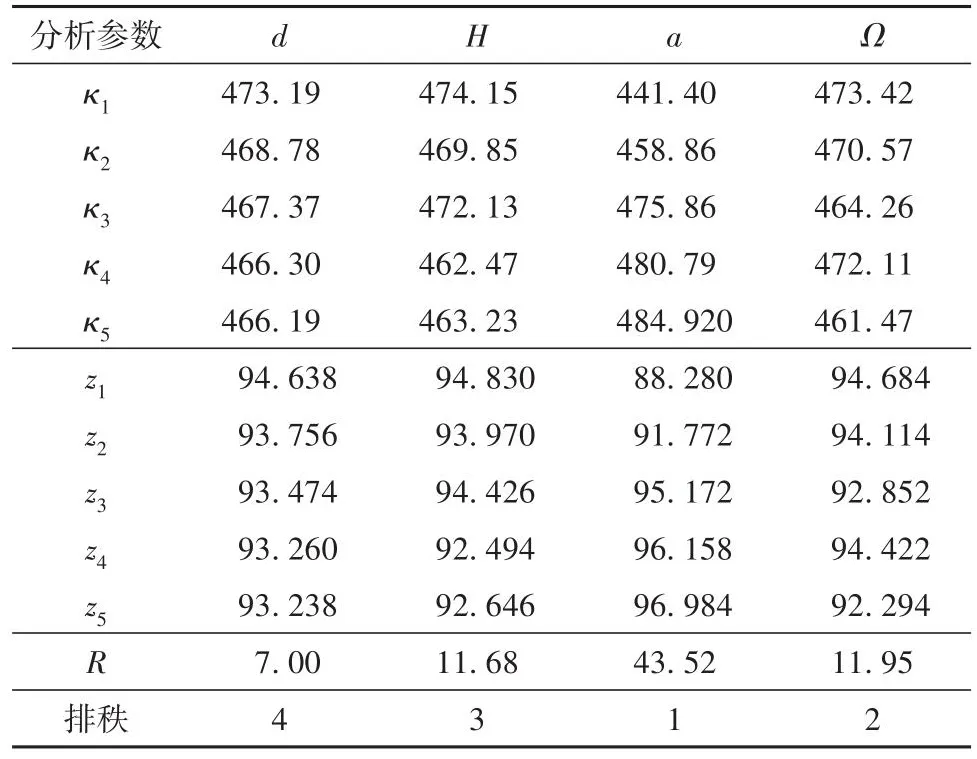
表4 以10～20 µm雾滴去除效率为响应值的极差分析Table 4 Range analysis with 10～20 µm droplet removal efficiency as the response value

4.3 以压降为响应值的极差分析

以压降为响应值的极差分析结果如表5所示。表5最后一行的排秩表明，不同因素在这5种取值范围内，对压降影响从大到小为：d、a、H。结果表明：d为影响压降的主导因素。同时根据z的大小可以发现，在参数范围内，压降均随着a的增大、d的增大、H的减小而增大。这是因为随着a的增大，烟气在除雾器内流动转向加剧；随着d的增大，入口处挡板面积也增大，在入口处流速方向与挡板垂直；在其他条件不变的情况下，随着H的减小，烟气流动的转向角度增加，从而增大了烟气的压降。该正交模拟试验中的最优组合为：d=100 mm，H=2 400 mm，a=540°。此时烟气流过除雾器的压降可达到最小。

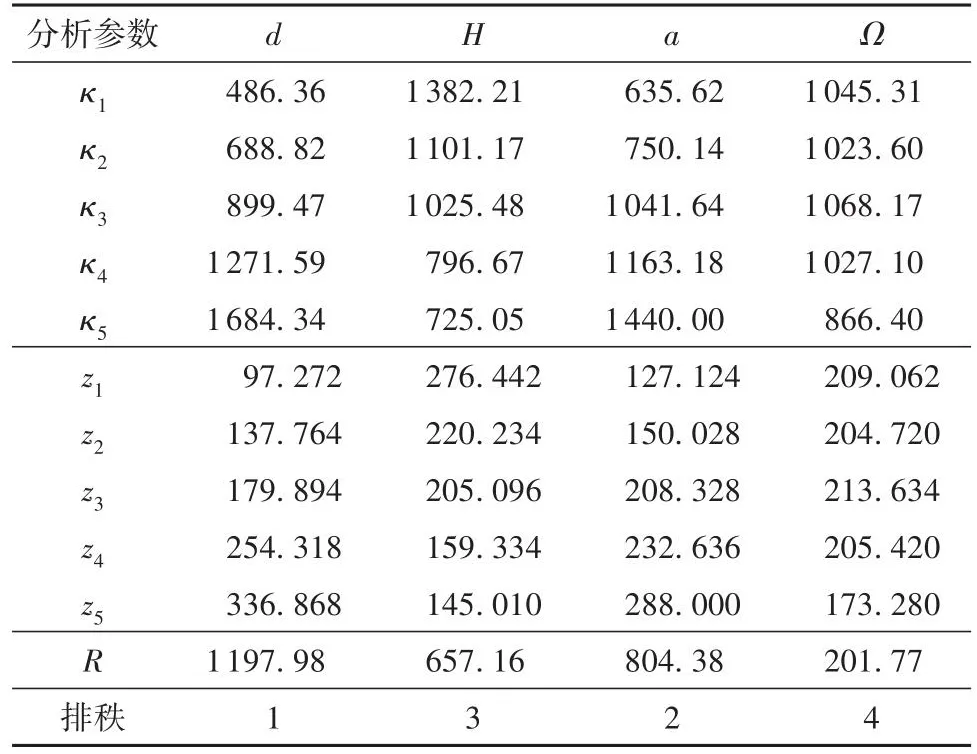
表5 以压降为响应值的极差分析Table 5 Range analysis with pressure drop as response value

可以看到，随着a的增大，可以显著提升对微细雾滴的去除效率，但过大的a会引起较大的压降；随着d的增大，入口处挡板面积增大，会引起较大的压降，同时除雾效率会降低。

综合以上分析，在实际应用过程中，在一定的流速范围内，若须大幅提高对微细雾滴的去除效率，优先提高扭转角。若要在提高除雾效率的同时将压降控制在工程允许范围内，不增加额外的设备，应选取合适的扭转角和单管直径，将压降控制在工程允许范围内。若需增大烟气的流通量，可以采用多个小管径的旋流管式除雾器进行并联运行。

5 结论

本研究设计了一种新型的旋流管式除雾器，对旋流管式除雾器内烟气流动进行模拟，并采用欧拉-拉格朗日方法，开展了对旋流管式除雾器的性能研究，并采用正交模拟实验研究了旋流管式除雾器的结构及运行参数对性能的影响，得出以下结论：

（1） 流速对直径小于10 µm的雾滴去除效率影响较小。对于基础型结构的旋流管式除雾器，在流速为3～7 m/s时，对直径在20～80 µm的雾滴去除效率在99%以上，对直径在10～20 µm的雾滴去除效率在86.5%以上，对直径在2～10 µm的雾滴去除效率在51.3%以上，压降为61.4～321.3 Pa。对微细雾滴的去除效率提升显著，且压降比较小，符合实际工程应用要求。

（2） 通过正交试验模拟得出了参数范围内各因素的最佳组合。以2～10 µm和10～20 µm的雾滴去除效率为响应值时，a的增大和d的减小有利于提高雾滴的去除效率，在实验组合中最优组合分别为为：d=100 mm，H=2 000 mm，a=900°和d=100 mm，H=1 600 mm，a=900°。以压降为响应值时，a的增大、d的增大、H的减小会加大烟气流过除雾器的压降，得到实验组合中最优组合为：d=100 mm，H=2 400 mm，a=540°。