三偏心蝶阀热棘轮效应的数值模拟

李树勋 张建正 尹会全 康雯宇 张博浩 王宜雪

（1.兰州理工大学 石油化工学院，甘肃 兰州 730050；2.机械工业泵及特殊阀门工程研究中心，甘肃 兰州 730050；3.陕西蓝箭航天技术有限公司，陕西 西安 710199）

在石油化工、核电与火电等高温低压大口径管线切断及控制领域，蝶阀以其结构紧凑、流阻小及启闭迅速等优势被广泛应用于管路系统。工程构件如管道、阀门、压力容器在使用中多数处于循环应力载荷状态，而棘轮效应的累积会致使构件产生过大的塑性应变［1-5］。棘轮效应的发生是随着循环周期的递增出现渐增性塑性应变累积，每个循环周期结束后变形不能恢复原状，出现残余变形。三偏心金属硬密封蝶阀在常温与高温交变循环载荷下会出现密封失效现象，此现象很大程度上可能与密封结构发生塑性变形有关。

目前，国内外学者对于棘轮效应的研究主要分为两个方面：一方面是对材料棘轮效应的研究，另一方面是对结构棘轮效应的研究。对于材料棘轮效应的研究，通常是利用弹塑性理论及本构理论建立材料的本构模型。Chellapandi等［6］采用Chaboche模型对G91钢的各种循环变形模式进行了研究，预测棘轮边界的累积棘轮应变。Rajpurohit等［7］通过改变应力参数，研究200个循环非对称循环加载对2.25Cr-Mo微合金钢室温拉伸行为的累积塑性应变的影响。Dwivedi等［8］研究了高强度低合金钢组织结构演变与棘轮变形的关系。Mishra等［9］研究了平均应力对9Cr-1Mo在室温和600 ℃下棘轮行为的影响规律，对比分析不同温度下，平均应力分别为0.26 MPa和0.20 MPa时的棘轮行为。姜金朋等［10］采用CS1026试验的应力应变滞回曲线和棘轮应变历程曲线确定不同Chaboche非线性随动强化模型的参数。

对于结构棘轮效应的研究，大多数文献通过有限元分析对真实工程构件进行棘轮行为研究及循环塑性分析。Varvani-Farahani等［11］通过棘轮-安定区域的边界和划分评价应力循环过程中的塑性变形累积。Tian等［12］利用用户材料子程序（UMAT）在ABAQUS有限元软件中对SA508-3钢的温度棘轮行为进行了数值模拟。Saravanan等［13］对304不锈钢直管在内压和循环弯曲联合载荷作用下的棘轮行为进行了数值模拟。Shi等［14］研究了Z2CND18.12N不锈钢弯管在恒内压和负载控制下反向弯曲作用下的棘轮变形。刘雪林等［15］基于RCC-M规范并采用薄壁圆筒近似公式对管道的热棘轮效应进行评价。王明毓等［16］采用Chaboche非线性随动强化模型对稳压器喷淋管线三通的热棘轮变形进行评定。陈小辉等［17］通过试验方式分析内压及循环位移对核电管道棘轮应变的影响。综上，目前在结构的棘轮效应方面，很少有学者采用非线性随动强化模型对复杂异形结构进行棘轮效应模拟分析与预测。

本研究以三偏心蝶阀为载体，采用Chaboche非线性随动强化模型进行热棘轮有限元分析，分析热棘轮效应对蝶阀密封副热变形及密封性能的影响，探究阀在数次常温与高温交变循环载荷下出现密封失效问题的原因。

1 棘轮效应及循环载荷下结构的力学行为

1.1 棘轮效应

在材料力学中，棘轮效应指材料在非对称应力控制循环加载下非弹性变形的累积，又称为棘齿效应或循环蠕变。当金属材料受到拉伸或压缩载荷作用时，如果应力过大超出材料的屈服强度，材料将会发生塑性变形。外力卸载并反向加载时，材料首先在弹性阶段恢复，继而发生反向塑性变形，如果反向施加的载荷小于初始正向载荷，那么材料的反向总变形就会小于正向总变形，进而产生残余应变。如此循环反复，就会出现塑性应变累积的现象，即材料发生棘轮效应［18］。三偏心蝶阀在数次常温与高温交变循环温度载荷下出现的密封失效问题，是由于蝶阀密封结构发生棘轮效应后产生渐增性塑性变形导致的密封失效。

1.2 循环载荷下结构的力学行为

在石油化工、航空航天及核电等特殊领域，压力容器和管道等承压设备工作条件较为复杂，往往同时承受循环的温度载荷、机械载荷及其他循环作用的耦合载荷，致使设备由于塑性变形累积而发生塑性垮塌或断裂［19］。

结构在承受循环载荷作用时，所产生的塑性应变不断累积增加，并最终导致结构破坏，这种效应就是棘轮效应。结构出现的棘轮效应力学行为如图1所示。图中：σS为屈服压力，σ为等效应力，ε为等效应变。

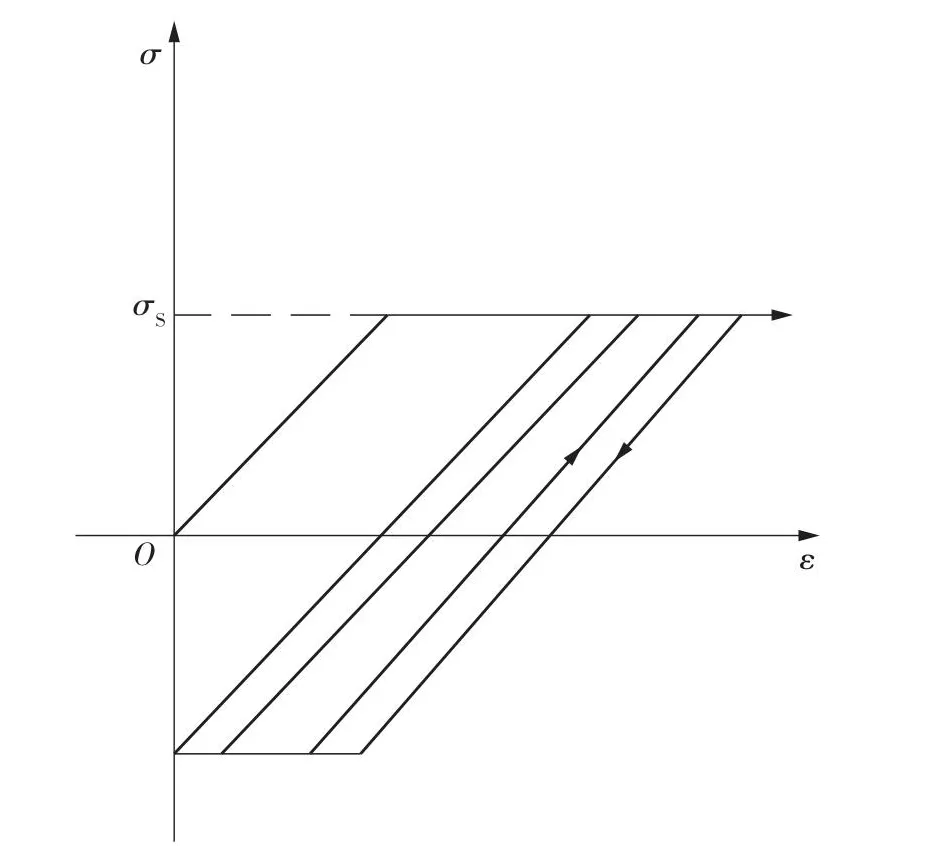
图1 棘轮效应示意图Fig.1 Schematic diagram of ratchet effect

2 Chaboche模型参数确定

Chaboche模型是由Lemaitre和Chaboche提出的一种基于Von Mises屈服准则的非线性随动强化模型，该模型表达式如下［20］：

式中：α为背应力张量；αi为第i个背应力分量，MPa；i为背应力的个数；σ为等效应力，MPa；dεp为等效塑性应变增量；Ci为初始运动硬化模量；γ为材料的特性参数。

对式（2）进行积分，可得

采用3组参数的Chaboche强化模型，则式（3）可写为

式中，γ1为增加的塑性变形个数，CF8的Chaboche本构模型参数参照文献［21］，屈服极限Sy为207 MPa，C1、C2、C3分别为115 000、65 000和1 310 MPa，γ1、γ2、γ3分别为3 700、600和2.75。

3 三偏心蝶阀热棘轮效应的有限元分析

由于蝶阀承受高低温循环载荷作用，因此蝶阀棘轮效应数值模拟是一个高度复杂并涉及3种非线性行为的有限元问题，蝶阀棘轮效应数值模拟流程图如图2所示。

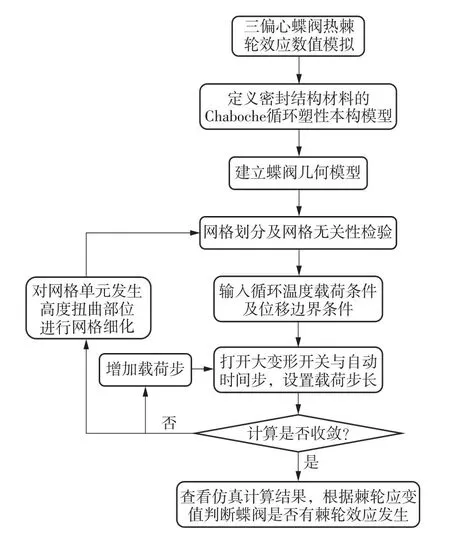
图2 棘轮效应数值模拟流程图Fig.2 Flow chart of numerical simulation of ratchet effect

增加载荷步是为了使迭代合力值线低于收敛准则线，而细化网格是为了使网格质量达到0.7以上，这两种方法都有助于计算收敛。

3.1 材料属性

三偏心蝶阀密封结构采用金属硬密封的形式。蝶阀工况参数为：公称通径DN200，公称压力PN16，工作温度650 ℃，适用于高温空气、熔盐、煤气等介质。阀体、密封圈等材料选用A351 CF8，屈服强度207 MPa（22 ℃）、98 MPa（650 ℃），阀杆、轴套等材料选用Inconel 625，屈服强度345 MPa（22 ℃）、266 MPa（650 ℃），主要零部件材料性能如表1所示。

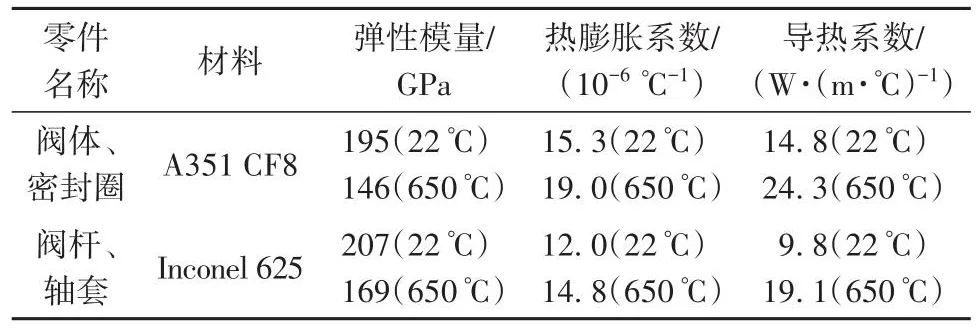
表1 蝶阀主要零部件材料性能参数Table 1 Material performance parameters of main parts of butterfly valve

3.2 几何模型

三偏心蝶阀二维剖视图如图3所示。对蝶阀常温工况与高温工况下的密封性能进行分析主要针对的是密封结构部分，并不涉及蝶阀散热架与驱动装置，因此只对阀体及密封结构建模，几何模型如图4所示。

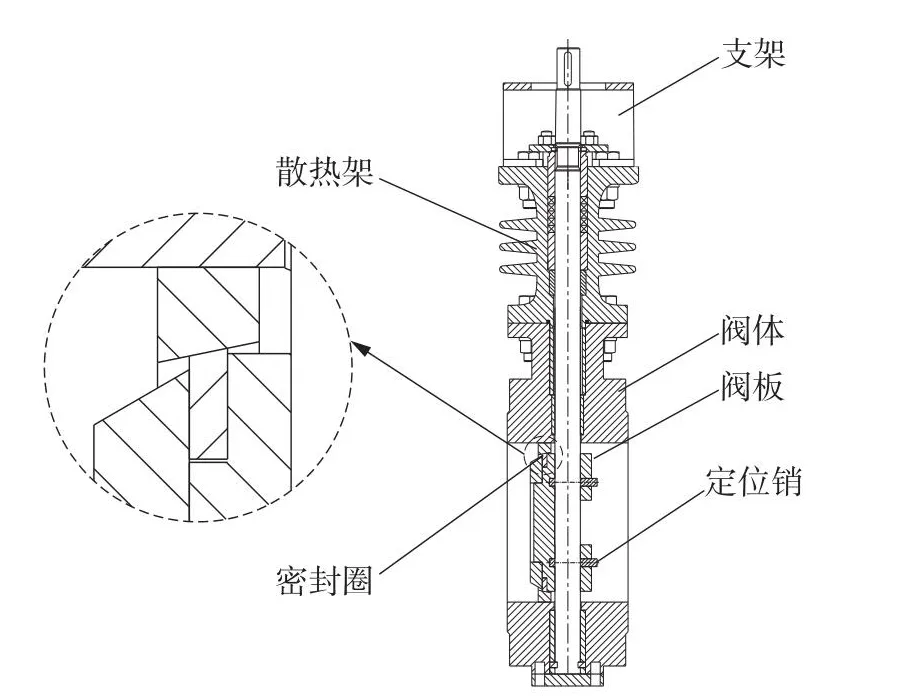
图3 三偏心蝶阀二维剖视图Fig.3 Two dimensional sectional view of three eccentric butterfly valve

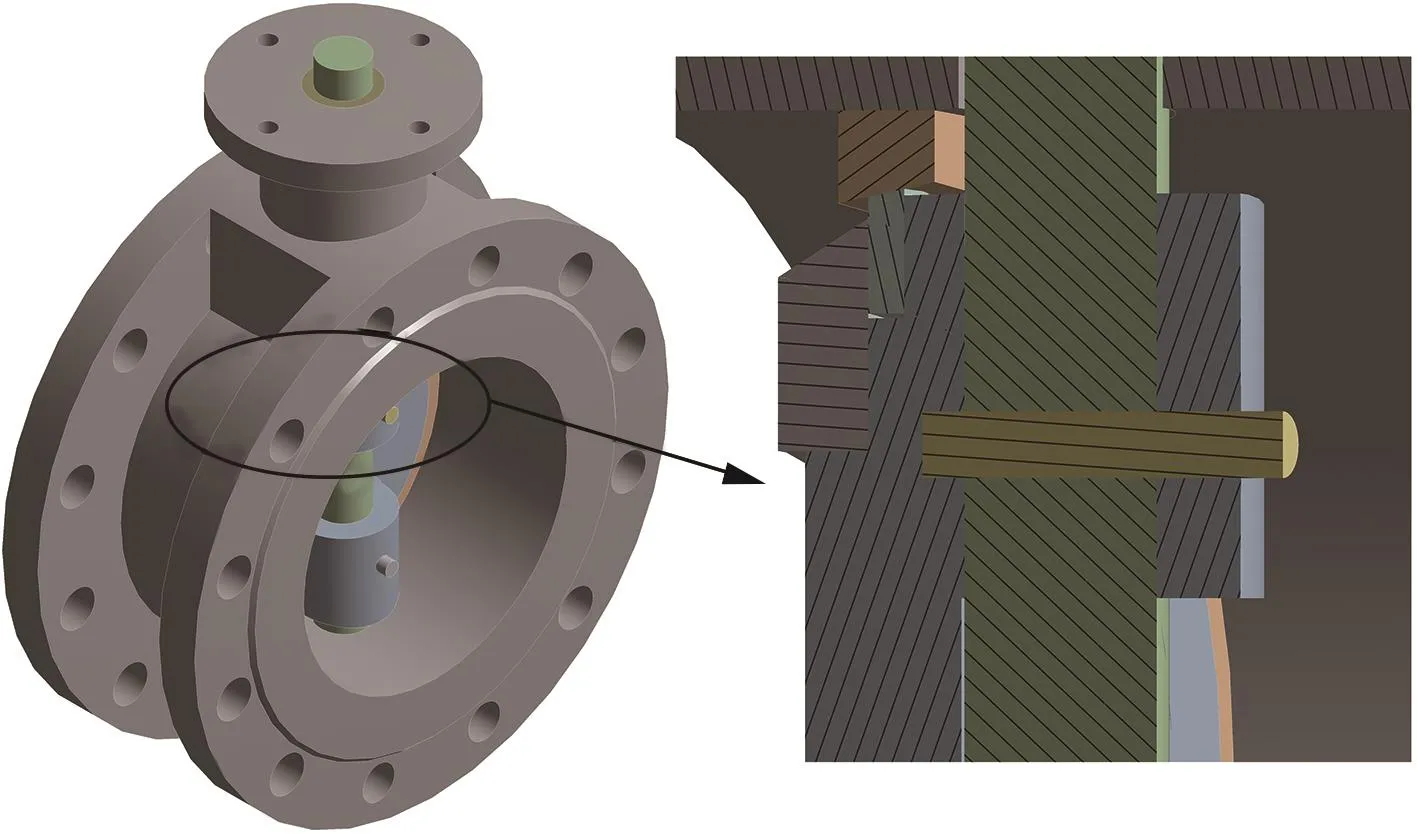
图4 三偏心蝶阀几何模型Fig.4 Geometric model of three eccentric butterfly valve

3.3 网格划分与网格无关性检验

将三偏心蝶阀简化后的几何模型导入ANSYS Workbench有限元分析软件，采用自适应网格划分和局部网格控制技术进行网格划分［22］。考虑到网格数量和网格质量对计算结果的影响，通过不断细化网格以保证相邻网格密度之间具有较小的数值分析误差。对模型进行网格无关性验证，单元数目为429 832时最大应力值是77.42 MPa，单元数目为478 236时最大应力值是81.01 MPa，单元数目为509 531时最大应力值是83.33 MPa，单元数目为530 612时最大应力值是83.89 MPa，单元数目为587 324时最大应力值是83.63 MPa。随着网格单元数目的增加，最大应力值相应增大，网格单元数目为429 832与478 236时的最大应力值相差4.6%，网格单元数目为478 236与509 531时的最大应力值相差2.8%，网格单元数目为509 531与530 612时的最大应力值相差0.67%，网格单元数目为530 612与587 324时的最大应力值相差0.31%，最终确定网格节点数目为805 186，网格单元数目为509 531，网格模型如图5所示。

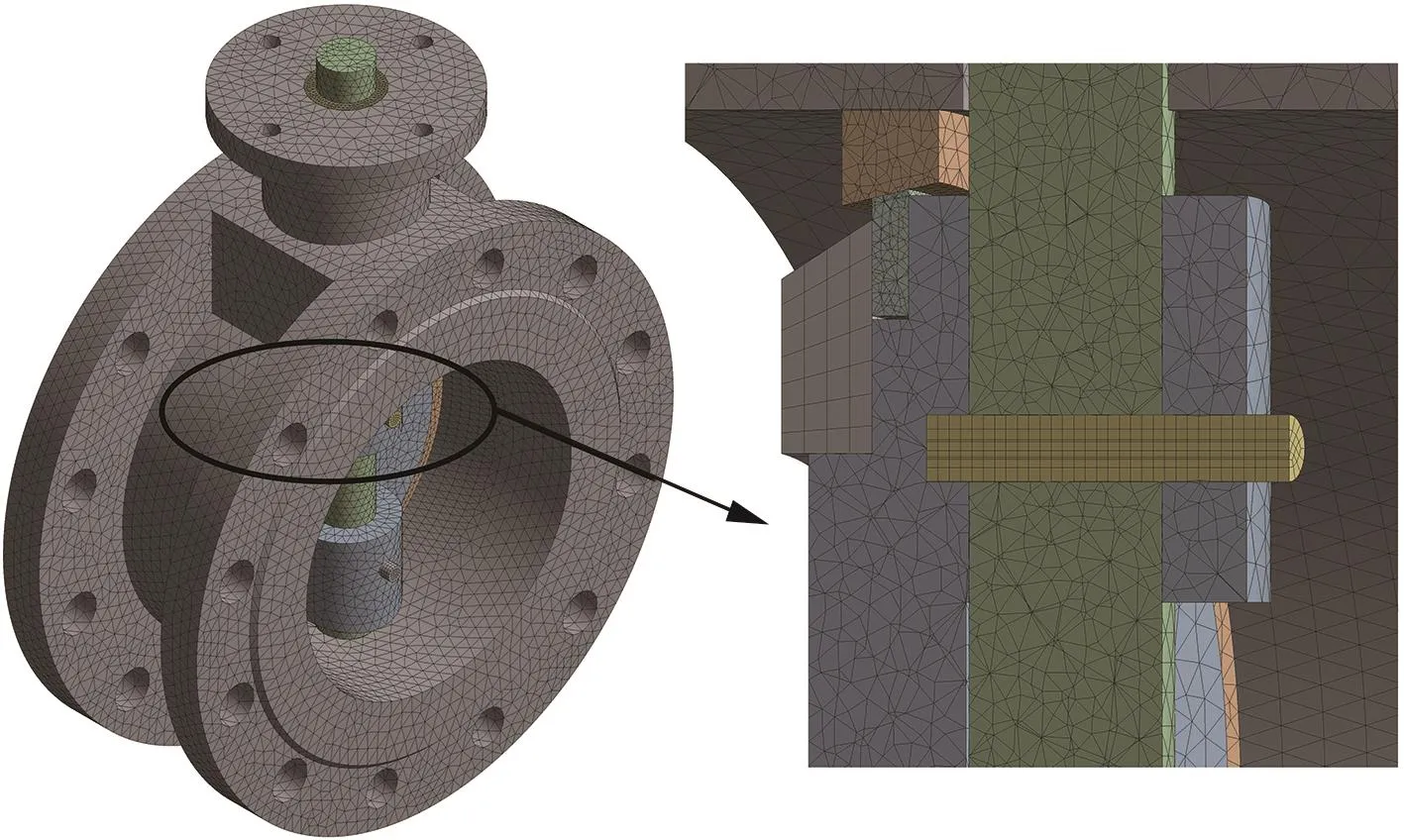
图5 网格模型Fig.5 Mesh model

3.4 载荷与约束施加

高温蝶阀在整个寿命周期内承受恒定的内压和循环温度载荷，循环温度载荷为22 ℃升温到650 ℃的过程以及650 ℃降温到22 ℃的过程，即随着介质温度的升高蝶阀内部与介质接触部位逐渐升温，升温到650 ℃以后保持一段时间，然后介质温度开始降低，内壁面温度相应地逐渐降低到常温22 ℃，如此反复。在阀杆上端环面施加扭矩800 N·m，在蝶阀内壁面与介质接触表面施加压力0.25 MPa，前10次循环工况下的载荷条件如图6所示。三偏心蝶阀进行循环温度载荷试验时外壁面与空气自然对流换热，自然对流换热系数取10 W/（m2·℃）。对阀体入口端法兰端面施加远端位移约束，阀体出口端法兰端面施加轴向自由约束。

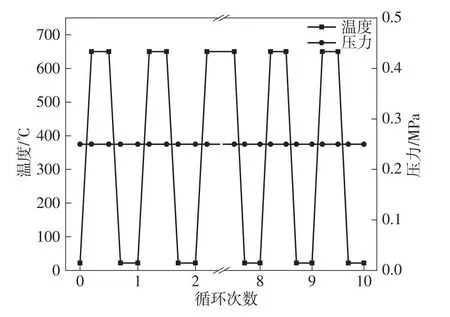
图6 前10次循环载荷Fig.6 Load of the first 10 cycles

3.5 棘轮效应有限元分析

3.5.1 循环温度场分析

根据第3.4节循环载荷边界条件对阀体内部施加循环温度载荷，为了保证计算的收敛性，升温与降温过程采用多载荷步方式施加，0～80个载荷步内共进行了10次温度循环，其中一个温度循环中升温过程与降温过程均采用4个载荷步完成。对蝶阀进行多载荷步循环温度场分析，得到蝶阀温度随载荷步的变化曲线，如图7所示。从图中可以看出，每个温度循环过程中蝶阀的温度场分布均相同，在高温工况时蝶阀最低温度、最高温度及平均温度分别为265.53、650.00和589.44 ℃。

图7 蝶阀温度随载荷步的变化曲线Fig.7 Variation curves of butterfly valve temperature with load step

高温工况下蝶阀温度场分布云图如图8所示，蝶阀最高温度分布在与介质接触的内壁面，最高温度为650 ℃，温度沿阀体壁厚方向呈梯度分布，从阀体内壁面到阀体外壁面逐渐减小，在两侧法兰处温度达到最低，最低温度为265.53 ℃。由于阀杆孔也有介质存在，阀体竖直方向的温度梯度较水平方向小，阀体上、下凸台及相邻法兰处的温度比法兰其他区域的温度高。

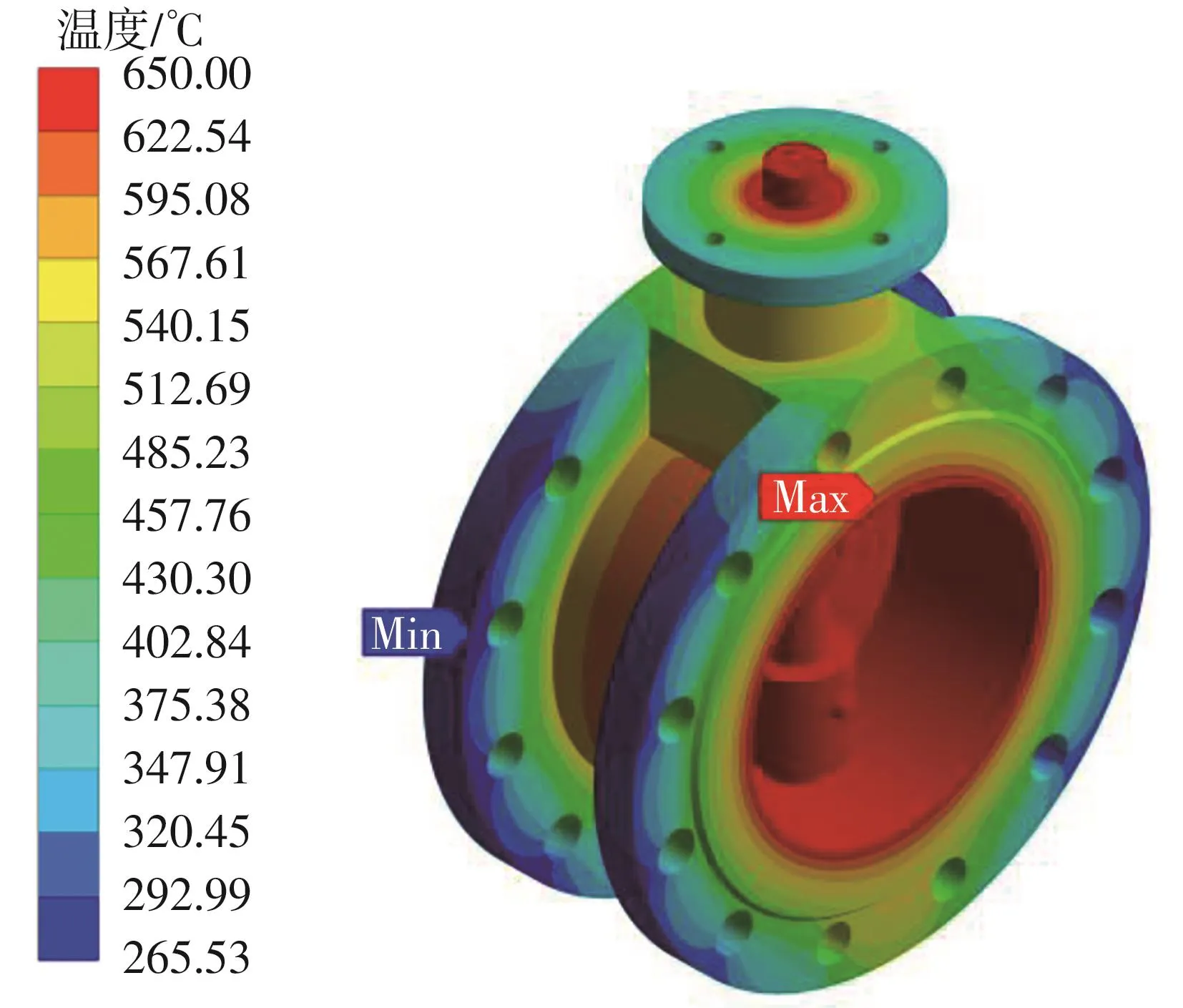
图8 蝶阀温度分布云图Fig.8 Temperature distribution nephogram of butterfly valve

高温工况下阀体温度场分布云图如图9所示，从阀座内环面到阀体外壁面温度逐渐降低，且阀座水平中心面沿厚度方向的温差梯度较竖直中心面明显，阀座内环面与阀体外壁面的最大温差大约为60 ℃。

3.5.2 热棘轮效应分析

将蝶阀各载荷步温度场分布结果导入结构场进行热棘轮效应有限元分析，温度场与结构场载荷步一一对应。导入所有的温度场结果，打开大变形开关以考虑几何非线性的影响；设置自动时间步，对蝶阀进行循环温度载荷下的有限元分析。根据有限元计算结果，可得到前10个温度循环阀座的最大塑性应变变化曲线，如图10所示。

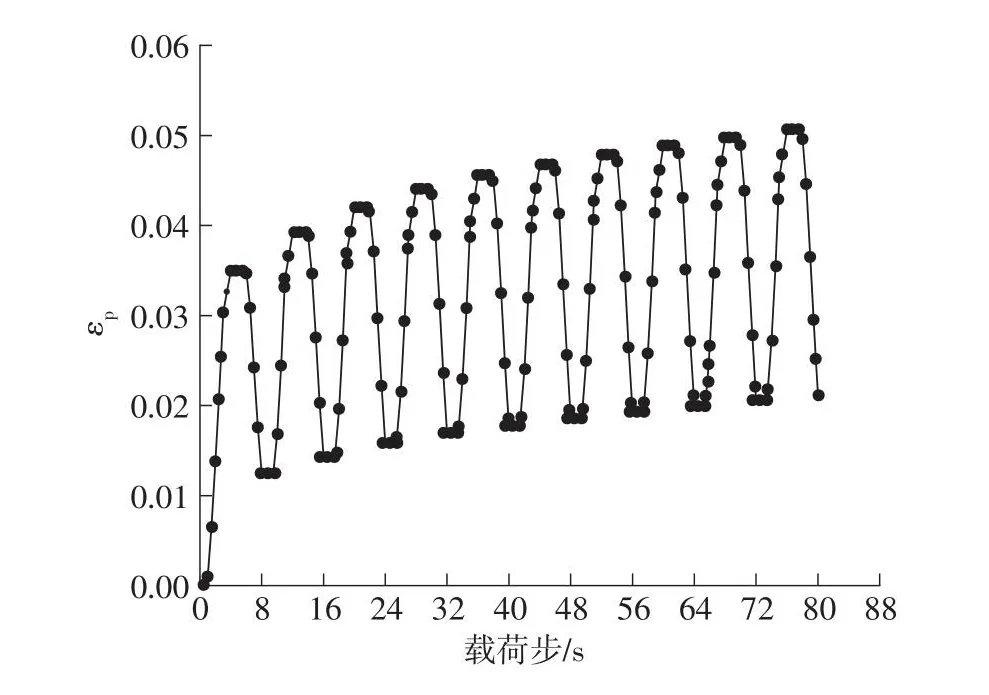
图10 前10个温度循环阀座的最大塑性应变变化曲线Fig.10 Maximum plastic strain curve of valve seat in the first 10 temperature cycles

从图10中可以看出，在温度循环的第1个周期内，随着介质温度从常温22 ℃到高温650 ℃的升温过程中，阀座最大塑性应变不断增大，在650 ℃时阀座最大塑性应变为0.034 98。当介质温度在650 ℃的高温保持阶段时，阀座最大塑性应变值不变，随着温度的降低，阀座最大塑性应变随之减小，在常温22 ℃时的塑性应变值为0.012 58。蝶阀在经历一个从常温到高温再到常温的循环之后，阀座最大塑性应变未能减小到0，即阀座发生塑性变形之后未能恢复原状。在随后的几个温度循环之后，阀体塑性应变不断累积，前10个温度循环中阀座的最大塑性应变为0.050 56，10个温度循环后最终在常温22 ℃时的最大塑性应变为0.021 16。

10个温度循环后阀座的塑性应变云图如图11所示。从图11可以看出，10个温度循环周期后阀座塑性应变云图沿竖直中心面与水平中心面均呈对称分布，即阀座斜锥面与直边面塑性应变云图大致相同、阀座上过渡面与下过渡面塑性应变云图大致相同，阀座最大塑性应变位于直边面大径边缘处，其值为0.021 6。阀座上、下过渡面局部区域塑性应变为0，这是由于阀体上、下侧设有凸台结构，壁厚相对较大，造成阀体上、下侧内外壁面的温差极小，因此未发生棘轮变形。阀体竖直中心面两侧为等壁厚的环面结构，内外壁面温差相对较大，因此阀座在常温和高温交变循环载荷的作用下发生棘轮变形。

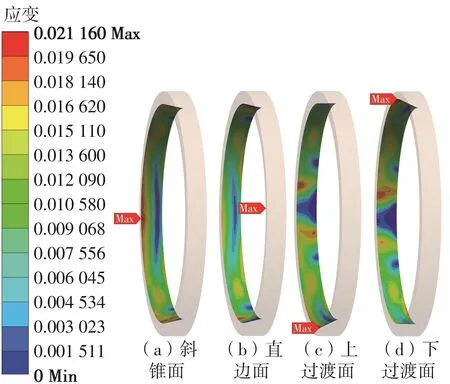
图11 阀座内环面各区域塑性应变分布云图Fig.11 Cloud diagram of plastic strain distribution in each area of inner ring surface of valve seat

为了研究10个温度循环后阀座内环面周向塑性应变分布情况，将阀座内环面沿轴向方向划分为五等份，即形成5条环线，对其依次编号如图12所示。在阀座内环面周向方向以15°为间隔提取一个节点塑性应变信息，监测点分布图如图13所示。

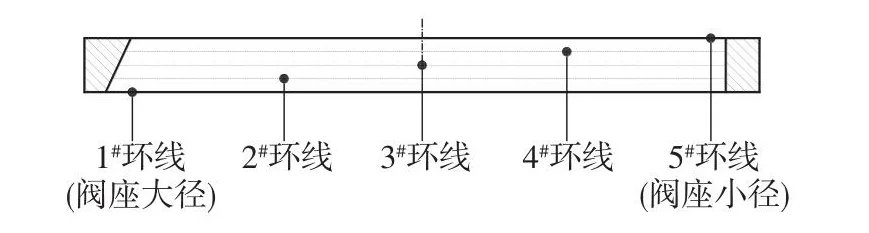
图12 阀座内环面等分示意图Fig.12 Isometric diagram of inner ring surface of valve seat

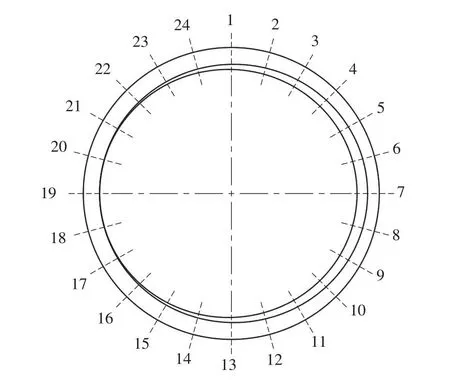
图13 阀座监测点分布Fig.13 Distribution of valve seat monitoring points

10个温度循环后阀座内环面周向塑性应变分布图如图14所示，阀座斜锥面（45°～135°）与直边面（225°～315°）区域的塑性应变大于阀座上过渡面（315°～45°）与下过渡面（135°～225°）区域的塑性应变，其中阀座1#环线（阀座大径）在直边面与斜锥面处的塑性应变最大。阀座各个环线的塑性应变均在0°与180°处达到最小，沿阀座轴向方向从1#环线（阀座大径）到5#环线（阀座小径）塑性应变逐渐减小，且上、下过渡面区域整体的塑性应变分布较直边面与斜锥面区域均匀。

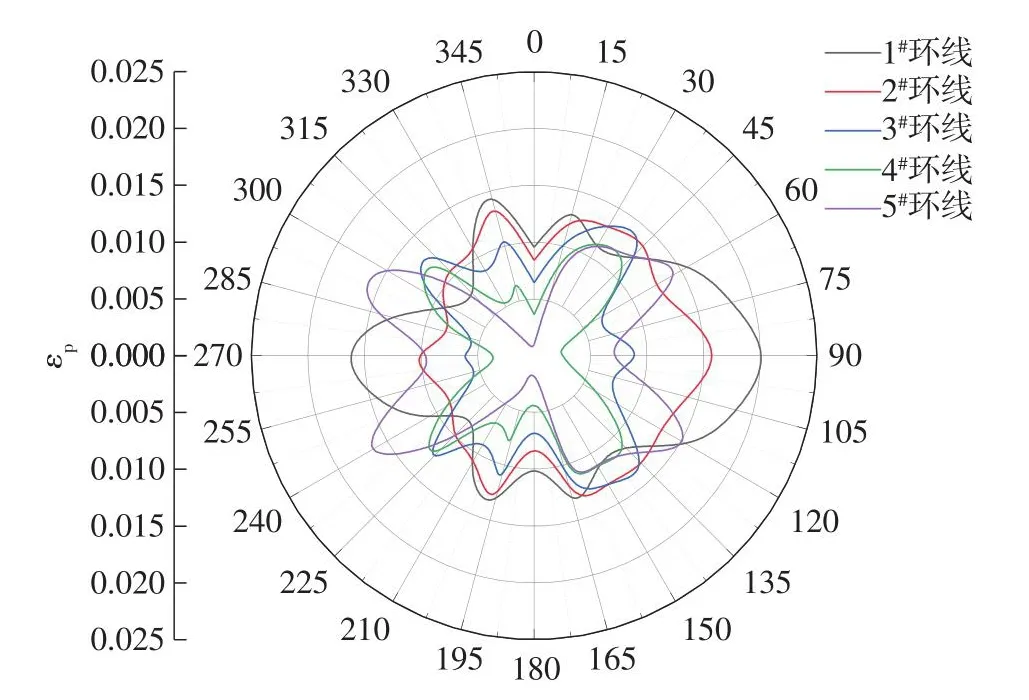
图14 阀座内环面周向塑性应变分布Fig.14 Circumferential plastic strain distribution of inner ring surface of valve seat

为了研究阀座发生棘轮变形后对蝶阀密封性能的影响，对10个温度循环后阀座内环面与密封圈外环面的径向变形进行分析。前10个温度循环阀座内环面径向变形变化曲线如图15所示。图中Dr表示阀座径向变形。从图中可以看出，阀座内环面的最大径向变形在一个循环周期内随升温过程逐渐增大，随降温过程逐渐减小，同时每个循环周期温度降低到常温后的最大径向变形随着循环周期的增加而不断增大，呈现出与最大塑性应变相同的变化趋势，10个温度循环后阀座内环面的最大径向变形为0.337 7 mm；最小径向变形在一个循环周期内的变化趋势与最大径向变形变化趋势相同，每个循环周期温度降低到常温后阀座内环面最小径向变形的变化趋势与最大径向变形变化趋势相反，10个温度循环后阀座内环面的最小径向变形为-0.273 2 mm，负号表示变形为径向收缩。

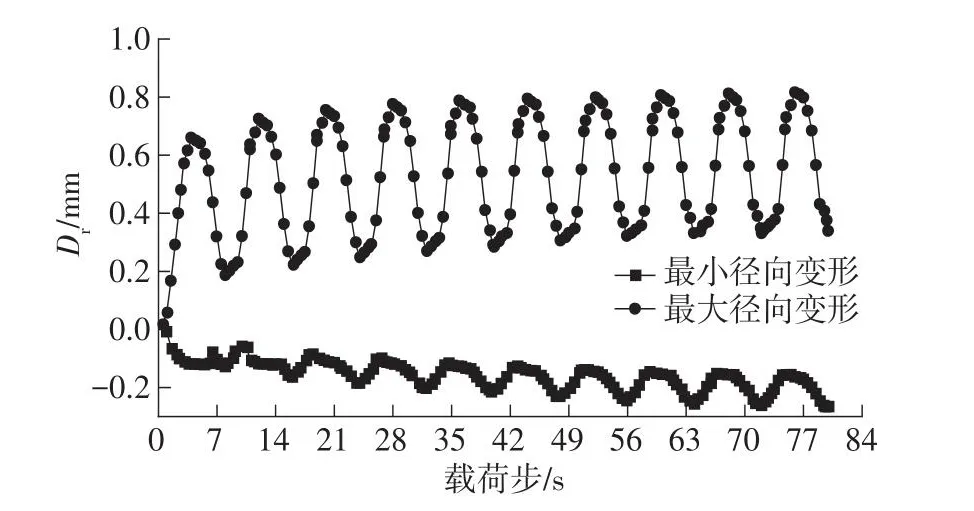
图15 前10个温度循环的阀座径向变形变化曲线Fig.15 Radial deformation curves of valve seat in the first 10 temperature cycles

在前10个温度循环过程中，密封圈与阀座随循环次数的最大径向变形如图16所示，密封圈在每个温度循环过程均为弹性变形，未发生棘轮效应，密封圈的最大径向变形为0.275 3 mm。从图中可以看出，在第5次温度交变循环之后，阀座的最大径向变形为0.284 4 mm，密封圈的最大径向变形为0.275 3 mm，阀座的最大径向变形大于密封圈最大径向变形，密封面出现间隙，间隙值为0.009 1 mm。在随后的温度循环过程中密封面间隙逐渐增大，最终导致三偏心蝶阀密封失效，出现泄漏现象。

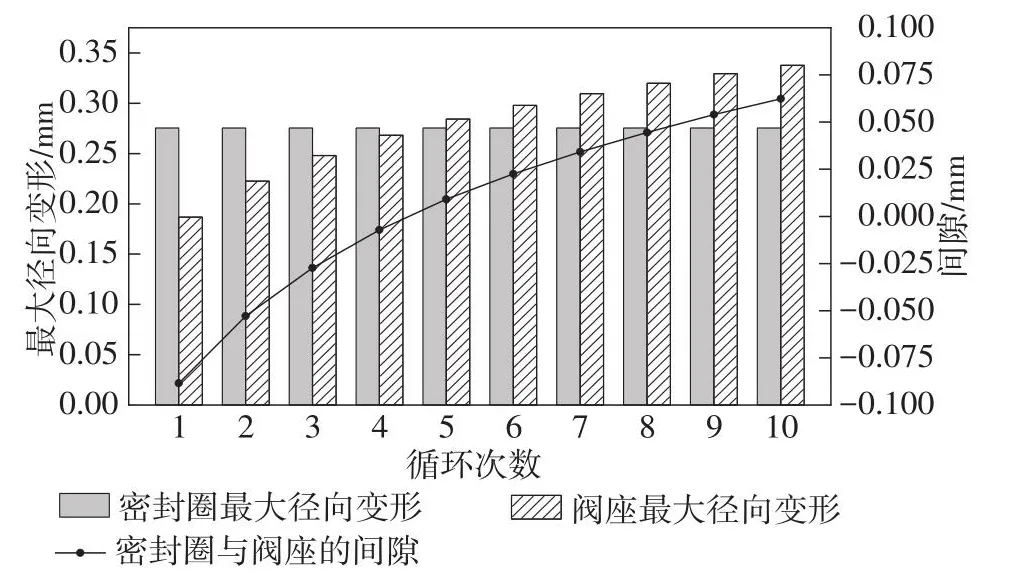
图16 密封圈与阀座随循环次数的最大径向变形Fig.16 Maximum radial deformation of seal ring and valve seat with the number of cycles

5个温度循环后阀座与密封圈环面的径向变形云图分别如图17、图18所示。从图17中可以看出，温度降低到常温后阀座斜锥面与直边面表现为径向膨胀，上、下过渡面表现为径向收缩，且对称区域的变形程度基本相同，其中最大径向膨胀量为0.284 4 mm，分布在阀座斜锥面大径处，最小径向收缩量为0.221 0 mm，分布在阀座下过渡面小径处。从图18中可以看出，温度降低到常温后密封圈上、下过渡面的径向变形一致且接近于0，而斜锥面区域的径向变形变现为向外膨胀，直边面区域的径向变形表现为向内收缩，因此密封圈在温度降低到常温后的径向变形实质上是由阀座直边面向阀座斜锥面平移的行为。密封圈最大径向膨胀量为0.275 3 mm，分布在密封圈斜锥面小径处，最小径向收缩量为0.155 8 mm，分布在阀座直边面小径处。

图17 5个温度循环后阀座环面径向变形云图Fig.17 Nephogram of radial deformation of valve seat ring after 5 temperature cycles

图18 5个温度循环后密封圈环面径向变形云图Fig.18 Nephogram of radial deformation of sealing ring after 5 temperature cycles

根据合作方对试验现象的描述，三偏心蝶阀在经历6次温度循环后出现内漏，数值模拟分析结果与合作方试验结果基本吻合。证明三偏心蝶阀出现密封失效现象是由于在常温与高温交变循环载荷的作用下蝶阀发生了热棘轮效应，阀座的残余变形导致密封面出现了间隙，进而引发泄漏。

4 蝶阀密封失效的防范措施

在第3节中三偏心蝶阀阀体外壁面与空气对流换热，阀体内壁面承受常温与高温交变循环载荷，在高温650 ℃时，阀座内环面与阀体外壁面的最大温差大约为60 ℃。阀座内环面与阀体外壁面之间的温差导致阀座产生较大热应力，在交变温度循环载荷的作用下阀座发生热棘轮效应，最终温度卸载到常温后阀座出现残余变形，阀座与密封圈存在间隙导致三偏心蝶阀密封失效。

英国压力容器规范BS 5500中对壳体的热棘轮效应作了定性说明：即在高温或低温下工作的压力容器应该缓慢加热或冷却，保冷和保热的效果要好，以尽量减小壳体上的温度梯度。因此，考虑对阀体外壁面进行保温处理。常用的保温措施有设置保温层、保温夹套、电伴热等，文章采用设置保温层［23］。在阀门热固耦合的时候，保温层的设置通常简化为绝热边界条件［24］。因此对保温良好的三偏心蝶阀进行常温与高温交变循环载荷下的热棘轮效应数值模拟分析，分析时对阀体外壁面施加绝热边界条件，进行网格划分及网格无关性检验。

通过有限元计算，得到10个温度循环后阀座环面的塑性总应变云图，如图19所示，最大总应变为0.000 124，阀座未发生热棘轮效应。10个温度循环后密封圈环面的塑性总应变云图如图20所示，最大总应变为0.000 366，密封圈未发生热棘轮效应。因此，密封圈与阀座在10个温度循环周期中所产生的变形均为弹性变形。

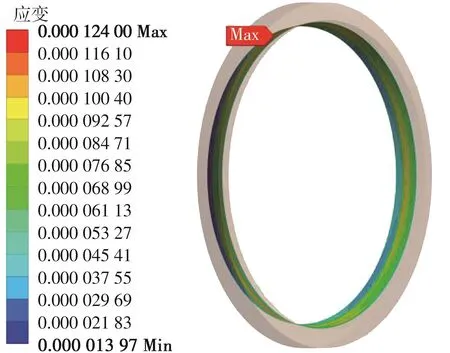
图19 阀座环面总应变云图Fig.19 Total strain nephogram of valve seat ring

图20 密封圈环面总应变云图Fig.20 Total strain nephogram of sealing ring

阀座与密封圈在经历10个温度循环周期后均未发生热棘轮效应，由此可见，对蝶阀阀体外壁面进行保温处理可以有效避免因热棘轮效应引发的密封失效问题。此外，对于承受常温与高温交变循环工况及常温与低温交变循环工况的阀门、压力容器及管道等设备进行保温处理也是避免发生热棘轮效应的有效措施之一。

5 结论

（1）基于Chaboche非线性随动强化模型对三偏心蝶阀进行10次常温与高温交变循环载荷下的热棘轮效应分析，在每个温度循环过程中蝶阀的温度场分布均相同，高温工况下阀座内环面与阀体外壁面的最大温差约为60 ℃。温度降低到常温后阀座的最大塑性应变随循环周期的增加出现渐增性塑性累积，10次温度循环后阀座的最大塑性应变为0.021 16，阀座在温度循环载荷的作用下发生热棘轮效应。

（2）第5次温度交变循环之后，阀座与密封圈的最大径向变形分别为0.284 4 mm和0.275 3 mm，阀座的最大径向变形大于密封圈的最大径向变形，阀座的残余变形导致密封面出现间隙，证明三偏心蝶阀出现密封失效现象是由于阀座发生热棘轮效应导致的。

（3）阀体外壁面进行良好保温后阀座未发生热棘轮效应，可以有效避免蝶阀在常温与高温交变循环载荷下出现密封失效问题。