电流自均衡的低纹波高增益双向直流变换器
王克英 黄毅 王子豪 余涛 吴毓峰 潘振宁
(华南理工大学 电力学院,广东 广州 510640)
随着全球能源危机的加剧,可再生能源的发展愈显重要,然而可再生能源具有输出功率不稳定的特点。综合能源系统作为一种先进的能量供应模式可以有效解决上述问题[1-3]。在直流综合能源系统典型拓扑中,储能电池通过双向DC-DC变换器(BDC)连接到高压直流母线,当可再生能源功率不足时需要BDC补充功率缺额,当可再生能源功率过剩时需要BDC吸收多余功率,因此储能单元中的BDC发挥着维持功率平衡的重要作用。
然而在实际应用中,系统的锂电池储能输出电压一般为直流48 V或更低,远小于380 V或以上的高压直流母线电压[4]。另一方面,以锂电池为载体的储能通常要求低工作电流纹波,以提升工作寿命[5]。因此,作为储能电池和高压直流母线之间的连接设备,综合能源系统要求BDC具有高电压增益、低电流纹波和功率双向流动特性。
针对高电压增益的需求,文献[6]提出一种级联型Boost变换器,其通过调整占空比可轻松实现高电压增益,然而该拓扑虽然结构简单但是主开关管依旧具有较大的电压应力。文献[7]采用了具有高电压增益的开关电容与开关电感技术,但这类BDC电流纹波大且负载调节有限,并不适用于储能系统。针对以上问题,文献[8]通过在开关电容低压侧串联滤波电感,可以有效抑制变换器的电流纹波,并保持高电压增益。
在此基础上,有学者对耦合电感技术展开了进一步的探索,将耦合电感与滤波电感结合,并利用耦合电感漏感电流实现了宽输入电压范围内的全范围软开关[9]。耦合电感在该类BDC中同时作为低压滤波电感和变压器存在,可满足低电流纹波和高电压增益的需求。因此耦合电感型BDC在高增益双向直流变换器的研究中逐渐被重视[10-12]。为进一步降低储能电池电流纹波,文献[13]在低压侧采用了两相交错耦合电感结构,结合相应的调制策略,低压侧电流纹波被有效抑制,低压侧大电流应力也被缓解。
然而受限于工艺技术,同一型号电力器件实际中也会存在工作参数不一致的问题,进而导致两相交错耦合电感的电流不均衡,而耦合电感中的不平衡电流会导致电感的磁芯饱和软开关丢失。因此,在变换器磁芯设计阶段需采用更佳的抗磁芯饱和设计,这会降低变换器的功率密度[14]。此外,也有学者通过在绕组中增加电流传感器并使用绕组电流改进变换器控制算法,有效避免了磁芯的饱和[15-17]。然而此类方法不但增加了变换器的成本而且增大了控制算法的复杂度。
基于此,本研究提出一种电流自均衡的高电压增益低电流纹波宽范围软开关的双向直流变换器。本研究提出的变换器无需复杂的控制即可实现电流自动均衡。同时该变换器低压侧采用交错耦合电感降低电流纹波,交错耦合电感同时作为变压器接入到高压侧混合钳位电路中实现更佳的电压增益。该变换器采用电压匹配控制策略,这种控制策略实现了功率控制与电压控制的解耦,降低了变换器的循环电流,拓宽了低压侧电压的工作范围,并保证了宽输入电压范围内的软开关。
1 电路结构和工作原理
1.1 电路结构和工作原理
电流自均衡双向直流变换器等效电路如图1所示。其中耦合电感L1由原边绕组Np1、副边绕组Ns1与励磁电感Lm1组成;耦合电感L2由原边绕组Np2、副边绕组Ns2与励磁电感Lm2组成,Lk为漏感。VH和VL分别代表高压直流母线侧电压和低压储能模块电压。CL1和CL2为低压侧钳位电容,CH1、CH2和CH3为高压侧钳位电容。S1-S4为低压侧开关管,Q1-Q4为高压侧开关管,D1和D2为高压侧钳位二极管。iL、iH、i1、i2、ip1、ip2、im1、im2和ileak分别为低压储能侧、高压母线侧、耦合电感L1、耦合电感L2、原边绕组Np1、原边绕组Np2、励磁电感Lm1、励磁电感Lm2和漏感Lk的电流。VC_L1、VC_L2、VC_H1、VC_H2和VC_H3分别代表CL1、CL2、CH1、CH2和CH3两端电压,电压正极方向由图1中电容旁正号表示。变换器可工作在升压和降压两种模式,在升压模式下,功率由低压侧传输至高压侧,在降压模式下,功率由高压侧传输至低压侧。为了便于分析,定义a、b两点间的电压为Vab,c、d两点间的电压为Vcd。
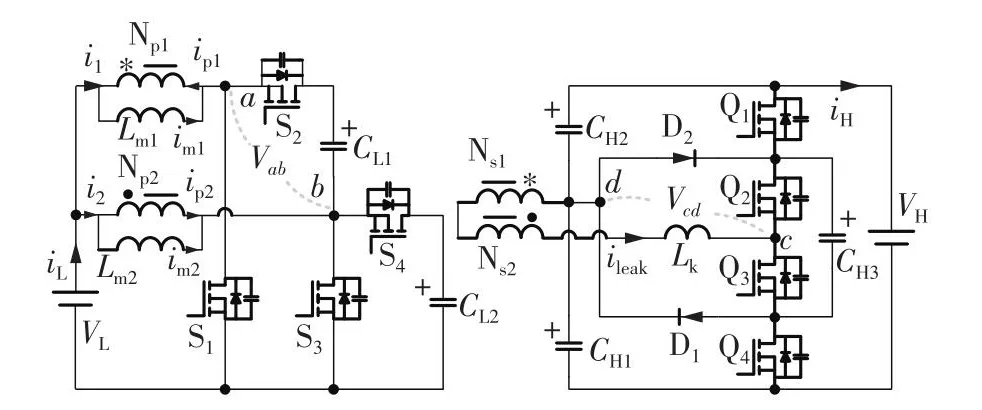
图1 电流自均衡双向直流变换器的等效电路Fig.1 Equivalent circuit of current self-balancing bidirectional DC-DC converter
变换器采用电压匹配加移相控制策略,共包含移相角φ和占空比D两个控制变量。电流自均衡变换器信号波形如图2所示。在图2(a)和(b)中,当Vab相位超前Vcd相位(φ>0)时,变换器工作在升压模式下,且随着移相角的增大变换器由轻载工作状态逐渐过渡到额定工作状态,输出功率逐步增大。当Vab相位滞后Vcd相位(φ<0),变换器工作在降压模式。漏感电流ileak斜率由Vab与Vcd共同决定,调整移相角φ可以实现对ileak信号波形的调整。如图2所示,ileak信号波形实际代表着低压侧电路与高压侧电路的功率交换大小与变换器的工作状态。
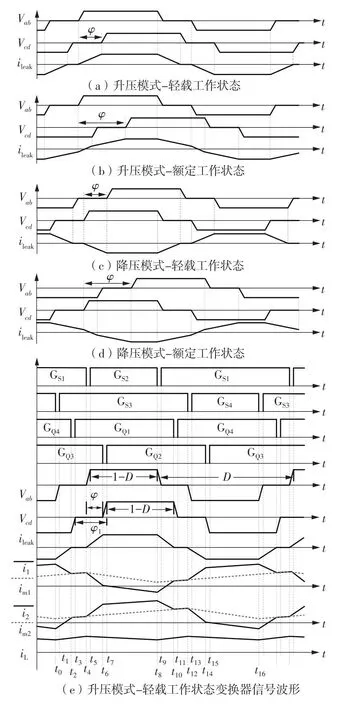
图2 电流自均衡双向直流变换器的信号波形Fig.2 Signal waveforms of current self-balancing bidirectional DC-DC converter
本文将以升压模式-轻载工作状态为例,阐述电流自均衡变换器的工作原理。图2(e)所示为该工作状态下变换器的信号波形,其中GS1-GS4和GQ1-GQ4分别为开关管S1-S4和Q1-Q4的驱动信号。可以看到,低压侧开关管S1(S3)和S2(S4)互补导通,S1与S3占空比均为D,且S3驱动信号相位滞后S1驱动信号相位180°。因此低压侧两相电流i1与i2相互交错抵消,从而减小低压侧电流iL纹波。高压侧开关管Q1(Q2)和Q4(Q3)互补导通,Q1与Q2的驱动信号占空比恒定为0.5,且Q2驱动信号相位滞后Q1驱动信号相位φ1,用以保持Vcd与Vab的脉宽一致。
当低压侧储能电池电压发生变化,通过调制低压侧占空比D,即可实现低压侧电压Vab与高压侧电压Vcd的幅值匹配,从而抑制ileak斜率并保持ileak信号波形的一致。
在电压匹配控制下,低压侧电压Vab与高压侧电压Vcd应满足:
其中,n为耦合电感L1和L2的匝比。Ns1和Ns2为耦合电感L1和L2副边绕组的绕组数。Np1和Np2为耦合电感L1和L2原边绕组的绕组数。
1.2 模态分析
根据图2(e)所示,变换器在一个周期内共包含16个工作模态。升压模式-轻载工作状态下电流自均衡变换器的主要模态等效电路如图3所示,其中虚线表示没有电流通过的线路,具体分析如下。
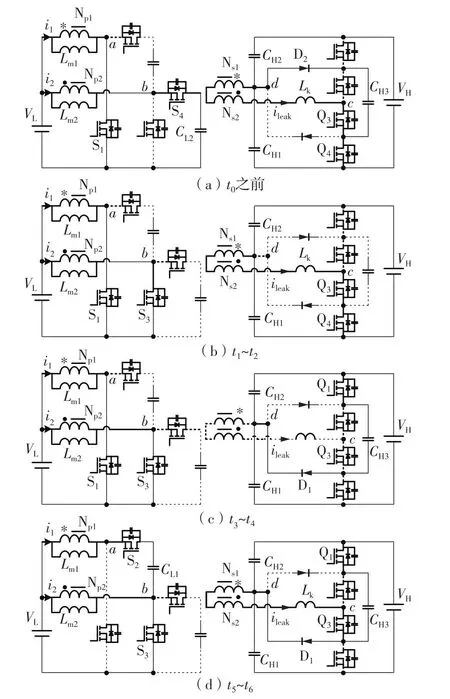
图3 升压模式-轻载工作状态电流的自均衡变换器模态Fig.3 Different modes of the current self-balancing converter under light-load operation in boost mode
模态1(t0之前):高压侧开关管Q3和Q4导通,Vcd电压为-VC_H1。低压侧开关管S1和S4导通,Vab电压为-VC_L2。励感Lm1通过VL充电,i1线性增大。励感Lm2、VL共同给CL2充电,i2线性下降。由于电压匹配技术的实现,有nVab=Vcd,漏感Lk两侧电势差为0,ileak斜率为0,ileak电流保持不变。
因此高压侧与低压侧电容电压满足如下关系:
模态2(t0~t1):在t0时刻,开关管S4关断。此时,由于i2的存在开关管S4的结电容电压将上升,开关管S3的结电容电压将下降直至为0。
模态3(t1~t2):在t1时刻,开关管S3导通并实现零电压开关(ZVS)。低压侧开关管S1和S3导通,Vab电压为0。Vcd电压为-VC_H1。漏感Lk两端电压为正,ileak线性增大直到为0。由于ileak的作用,i1和i2分别线性下降和线性上升。
在模态2与模态3期间,ileak满足:
模态4(t2~t3):在t2时刻,ileak线性减小至0,Q4在零电流开关(ZCS)条件下关断。
模态5(t3~t4):在t3时刻,开关管Q1导通,Vcd电压为0,而Vab电压也同样为0。ileak保持不变并维持零电流状态。在此过程中,励磁电感Lm1和Lm2两端电压为VL,i1和i2线性增大。
在模态4与模态5期间,漏感电流满足:
模态6(t4~t5):在t4时刻,开关管S1关断。此时,由于i2的存在开关管S1的结电容电压将上升,开关管S2的结电容电压将下降直至为0。
模态7(t5~t6):在t5时刻,开关管S2导通并实现ZVS。低压侧开关管S2和S3导通,Vab电压为VC_L1。Vcd电压为0。漏感Lk两端电压为正,ileak正向线性增大。由于ileak的作用,i1和i2分别线性下降和线性上升。
在模态6与模态7期间,漏感电流满足:
模态8(t6~t7):在t6时刻,开关管Q3关断。此时,由于ileak的存在开关管Q3的结电容电压将上升,开关管Q2的结电容电压将下降直至为0。
由于工作模态具有对称性,因此只需要分析前8个工作模态即可完成全模态的分析。结合式(5)-(7)可以得到关键时刻漏感电流ileak:
其中T为开关管的工作周期。
2 电路特性分析
2.1 电压增益
根据励感Lm1与Lm2的伏秒平衡原理,可得低压侧电容CL1与CL2两端的电压与低压侧储能接口电压关系为
通过高压侧电容分压关系,可以得到高压侧母线电压表达式:
结合式(2)-(4)和式(9)-(10),可得本变换器电压增益为
由式(11)可知,电流自均衡变换器的高电压增益来源于多级电路的电压增益。变换器低压侧电路提供基础电压增益,该增益由式(9)表示。耦合电感匝比为变换器提供第二级电压增益,该增益由式(2)-(4)表示。高压侧电路作为第三级电压增益,该增益由式(10)表示。
2.2 传输功率
如图2(e)所示,忽略传输损耗,本变换器的传输功率P可通过Vcd与ileak表示:
其中漏感电流ileak已由式(8)给出,进一步结合式(12)可得升压模式-轻载工作状态的传输功率为
同理可得本变换器在其他模式和状态下的传输功率表达式,如表1所示。在表1公式的基础上,基于Matlab平台绘制了不同模式和状态下传输功率P随移相角φ和占空比D变化的曲面(见图4(a)),其中曲面颜色越浅表示正传输功率越大。可见本变换器在移相角φ>0时具有正的传输功率,而在移相角φ<0时具有负的传输功率,因此本变换器可方便地实现传输功率方向的控制。另一方面,本变换器在不同模态和状态下,传输功率P与移相角φ都具有良好的单调性与斜率,因此反馈控制单元在此功率曲面上可方便地实现传输功率的大小控制。图4(b)为本变换器的控制框图,由电压匹配控制和移相控制组成,图中Pref表示变换器的目标功率。其中占空比D由VH和VL确定,而传输功率由移相角φ通过比例积分控制(PI)实现独立调节。因此通过占空比D和移相角φ可以分别实现电压匹配控制和功率控制,从而实现两种控制的解耦。由于两种控制解耦,因此通过调整移相角φ,即使用移相控制方法,便可以灵活控制传输功率的方向与大小。

表1 传输功率表达式Table 1 Transmission power expression

图4 电流自均衡直流变换器功率传输曲面与控制框图Fig.4 Power transfer surface and control diagram of current self-balancing DC-DC converter
2.3 软开关特性
电流自均衡直流变换器中开关管的软开关依赖于储存在耦合电感中的能量。对于低压侧电路,其依赖于耦合电感一次侧电流i1与i2。对于高压侧电路,其依赖于耦合电感二次侧电流ileak。
由于电流自均衡变换器运行模式具备对称性,本节以升压模式为例对其软开关特性展开分析。
如图1和图2(e)所示,低压侧上桥臂开关管S2在t4时刻关断,励感电流im1达到最大值且i1与im1相等,较大的相电流i1使开关管S2体二极管轻易导通,从而实现ZVS。
相对而言,低压侧下桥臂开关管S1的ZVS条件是在t8时刻有足够的反向相电流i1。此时,必须有ip1大于im1,才能产生反向电流进而保证S1实现ZVS,此条件较难实现。
因此,对于低压侧下桥臂开关管S1与开关管S3的ZVS条件可以表示如下:
在高压侧,由图3和模态分析过程可知,开关管Q1与开关管Q4可以实现ZCS。开关管Q2与开关管Q3的开关情况类似,且均由ileak提供反向电流。与此同时,为了保证Q2与Q3在轻载下的ZVS,漏感能量需要高于结电容中的能量:
其中,CQ2和CQ3分别为开关管Q2和Q3的结电容,VQ2和VQ3分别为开关管Q2和Q3漏源极间的电压。
结合式(14)与式(15),可知耦合电感参数应该满足:
上述推导说明,当励感Lm与漏感Lk在任意占空比D和移相角φ均满足式(16)时,电流自均衡直流变换器可实现软开关。因此通过耦合电感参数设计,电流自均衡直流变换器可实现低压电压与变换功率的宽范围软开关。
2.4 电流自均衡机理
电流自均衡为本变换器的重要内容,其具体含义为耦合电感L1与L2的平均电流i1_ave与i2_ave相等。不同于其他使用附加电流传感器与反馈算法的电流均衡方案,本变换器利用低压侧钳位电容CL1和CL2的安秒平衡特性即可实现拓扑级电流自均衡。
电流自均衡双向直流变换器的电流自均衡工作原理如图5所示。图5(a)和图5(b)分别为本变换器在t4~t8和t12~t16期间的工作情况,在此期间电流i1和i2分别对钳位电容CL1和CL2充放电。
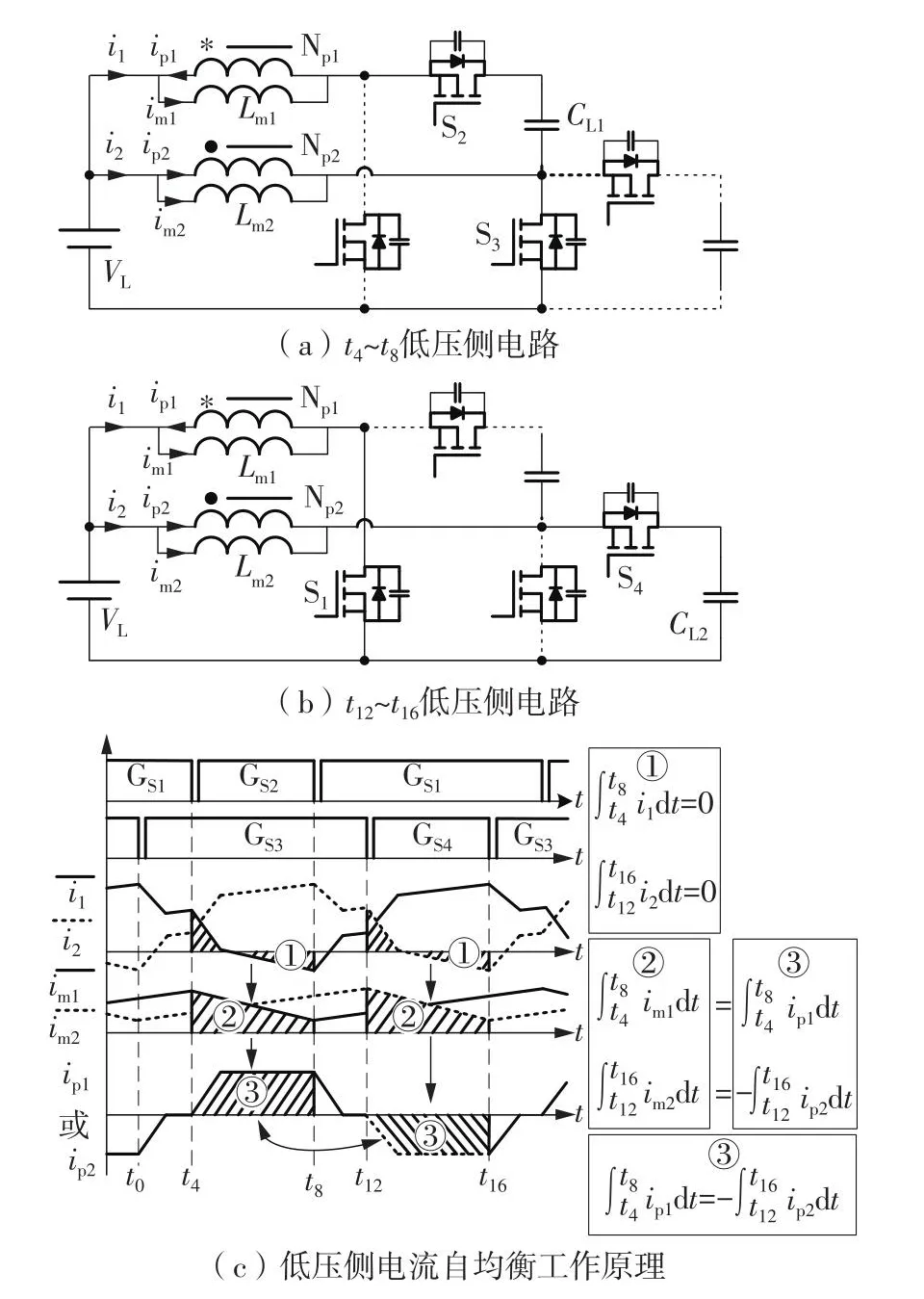
图5 电流自均衡双向直流变换器电流自均衡工作原理Fig.5 Current self-balancing principle of current self-balancing bidirectional DC-DC converter
图5(c)示出了在一个开关周期t4~t8和t12~t16期间低压侧电流的关系。由于钳位电容CL1与CL2只在t4~t8和t12~t16期间被充放电,因此根据电容的安秒平衡特性,图中①对应的i1与i2曲线积分为0:
其中,iC_L1和iC_L2分别表示流过低压侧电容CL1和CL2的电流,电流参考方向根据其电压取关联参考方向。
im1、im2与ip1、ip2在对应时间的积分应该相等,即图中②对应im1和im2曲线的积分与图中③对应ip1和ip2曲线的积分相等:
由于耦合电感副边绕组Ns1和Ns2与漏感Lk串联,因此有:
在模态分析小节中,对高压侧漏感电流ileak已进行定量分析。由式(8)可知,漏感电流ileak具有对称性,则对应到原边绕组电流ip1和ip2中,其在对应时间的积分相等,即图中③对应曲线的积分面积应该相等:
因此,结合图中③与图中②的关系,图中②对应im1和im2曲线的积分相等。
而由于im1和im2为三角波,其在图中②对应的积分已经可以表示出im1与im2的均值,所以im1与im2的平均值相等:
实际上,由于原边绕组电流ip1和ip2具有对称性,也即是周期积分为零,因此耦合电感L1电流均值i1_ave等于其励感电流平均值im1_ave:
结合式(21)Lm1与Lm2的电流平均值im1_ave与im2_ave相等,则可得证,耦合电感低压侧的平均电流相等:
2.5 低电流纹波特性
对于使用耦合电感的BDC,低压侧电流纹波主要来源于两方面,一方面是低压侧耦合电感的励感Lm1和Lm2周期性充放电而引入的纹波电流Δim,另一方面是耦合电感的绕组Np1和Np2与高压侧电路交换能量而引入的绕组电流ip。电流自均衡双向直流变换器的低电流纹波特性如图6所示。图6(a)示出了本变换器低压侧拓扑电路,由于耦合电感绕组电流ip1与ip2相等,两绕组电流ip1与ip2相互抵消,不参与低压侧电流纹波的产生。图6(b)示出了本变换器低压侧两对开关管GS1-GS2与GS3-GS4的交错开关过程,低压侧耦合电感的励感电流im1与im2纹波相互交错抵消,从而实现了低压侧的低电流纹波特性。
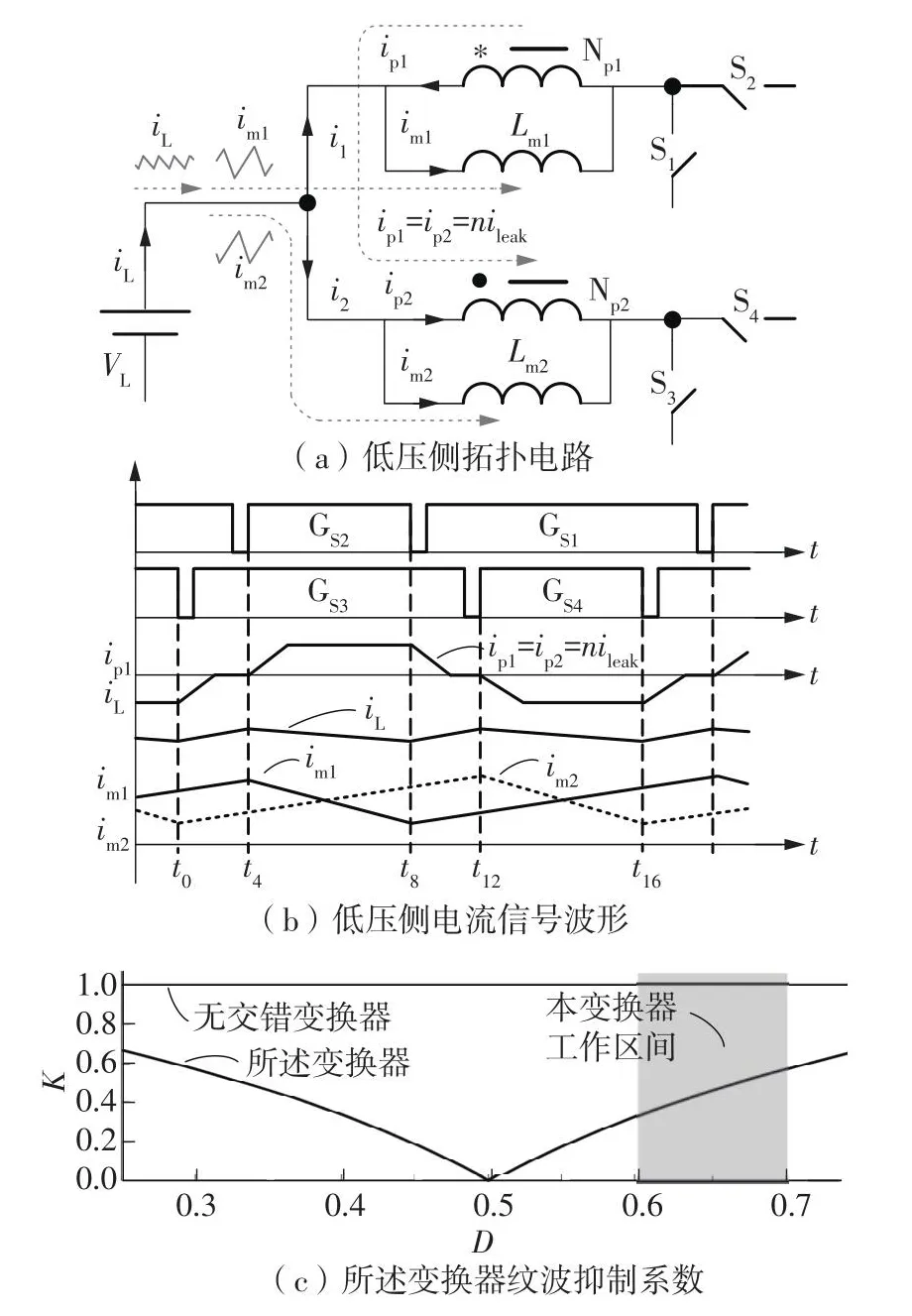
图6 电流自均衡双向直流变换器低电流纹波特性Fig.6 Low current ripple characteristics of current selfbalancing bidirectional DC-DC converter
对于无交错技术的BDC,其纹波电流即是励感纹波电流Δim。在t0~t12内,励感电流im线性增大可以计算得到其纹波电流大小:
对于使用交错技术的BDC,其电流纹波由两交错im产生。t8~t12内,低压侧电流iL线性增大可以计算得到其纹波电流大小:
定义变换器纹波抑制系数K为ΔiL与Δim之比,在本变换器的工作区间内可表示为
如图6(c)所示,本变换器的纹波抑制系数K,在工作区间内小于0.57,有良好的电流纹波抑制效果。
3 与现有BDC比较
为了突出本变换器的优势,选取相近拓扑的直流变换器作为本研究的比较对象。表2示出了本变换器与文献[8]、[13]和[17]的参数比较情况。

表2 与现有BDC的性能比较Table 2 Comparison between the proposed converter and the existing BDCs
对本变换器的优势可以进行如下总结:
1)本研究提出的变换器具有高电压增益优势:文献[17]虽然实现了电流的算法均衡,然而4个耦合电感只被用于均流,对提高电压增益方面没有发挥作用。相比文献[17],文献[8]使用了开关电容实现了2倍电压增益,然而为了弥补开关电容的大电流纹波,其需要低压侧串联335 µH大电感抑制电流纹波,无法引入更多磁性原件提高电压增益。相比文献[8],本变换器通过引入低压侧钳位电容和交错耦合电感,在保持电流自均衡的条件下,将耦合电感作为变压器复用进一步实现了电压增益的n倍提高。
2)本研究提出的变换器具有低电流纹波优势:文献[13]虽然与本变换器具有相似电压增益和拓扑结构,然而其低压侧却有12.60 A的电流纹波,该电流纹波将缩短锂电池模组的工作寿命。本变换器将变压器与电感复用为交错耦合电感结构,即省去变压器而增大耦合电感,因此其低压侧电流纹波为3.27 A,对锂电池模组更为友好。
3)本研究提出的变换器具有电流均衡优势:虽然文献[8]与[13]有较优的电流纹波和电压增益,然而却都未解决电流均衡的问题。文献[17]虽然实现了电流均衡,然而却要使用4个大感值耦合电感以辅助算法实现均流,此方案严重限制了BDC的功率密度和高电压增益。本变换器仅在低压侧使用钳位电容配合耦合电感,无需附加传感器和复杂控制方法,即可实现电流的自动均衡,对实际的BDC生产更有意义。
4 实验验证
为了验证本变换器的可行性,设计并制作了一款1 kW的实验样机,如图7所示。样机所用控制器为TMS320F28335,具体实验参数如表3所示,其中Lm1、Lm2和Lk的取值由式(16)计算得到,而低压钳位电容CL1-CL2与高压钳位电容CH1-CH3则以电容电压纹波小于5%为准来选定。
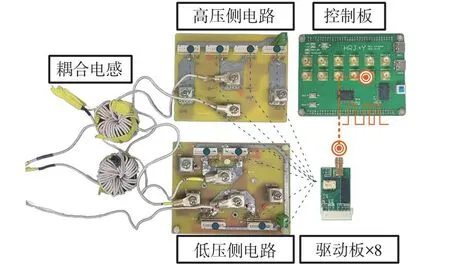
图7 电流自均衡双向直流变换器实验样机的主电路Fig.7 Main circuit of experimental prototype of current selfbalancing bidirectional DC-DC converter
电流自均衡直流变换器在升压模式和降压模式下额定功率的关键波形如图8和图9所示。其中图8为变换器升压模式下工作波形,图9为变换器降压模式下工作波形。

图8 升压模式下本变换器额定功率下的信号波形Fig.8 Signal waveforms at rated power of the proposed converter under boost mode

图9 降压模式下本变换器额定功率下的信号波形Fig.9 Signal waveforms at rated power of the proposed converter under buck mode
观察图8(a)和图8(c)可知,本变换器可以实现不同输入电压下的电压匹配,保证了n Vab_max=Vcd_max,从而降低了变换器的循环电流。图8(b)和图8(d)验证了变换器的低电流纹波与电流自均衡特性,可以看到,两个耦合电感电流i1与i2大小相等且相互交错,有效地降低了低压侧总电流iL的电流纹波。此外,对比图8和图9可以发现,本变换器在升压模式和降压模式中工作波形基本类似,其不同点仅在于两种模式中移相角大小和电流方向相反。实验结果表明,本变换器可通过移向角控制功率传输方向。
电流自均衡直流变换器在额定功率下软开关波形如图10所示,由于S1(S2)和S3(S4)软开关条件一致,故此处仅给出开关管S3和S4软开关波形,其中包括低压侧开关管的驱动信号GS3和GS4以及对应的开关管漏源极电压VS3和VS4和对应的耦合电感电流i2。以图10(a)为例,开关管驱动信号GS3上升沿滞后于开关管漏源极电压的下降沿,开关管实现了零电压开通。进一步,由图10可知,本变换器不论在升压模式还是降压模式,其低压侧开关管均可实现零电压开通,从而保证变换器的高效运行。
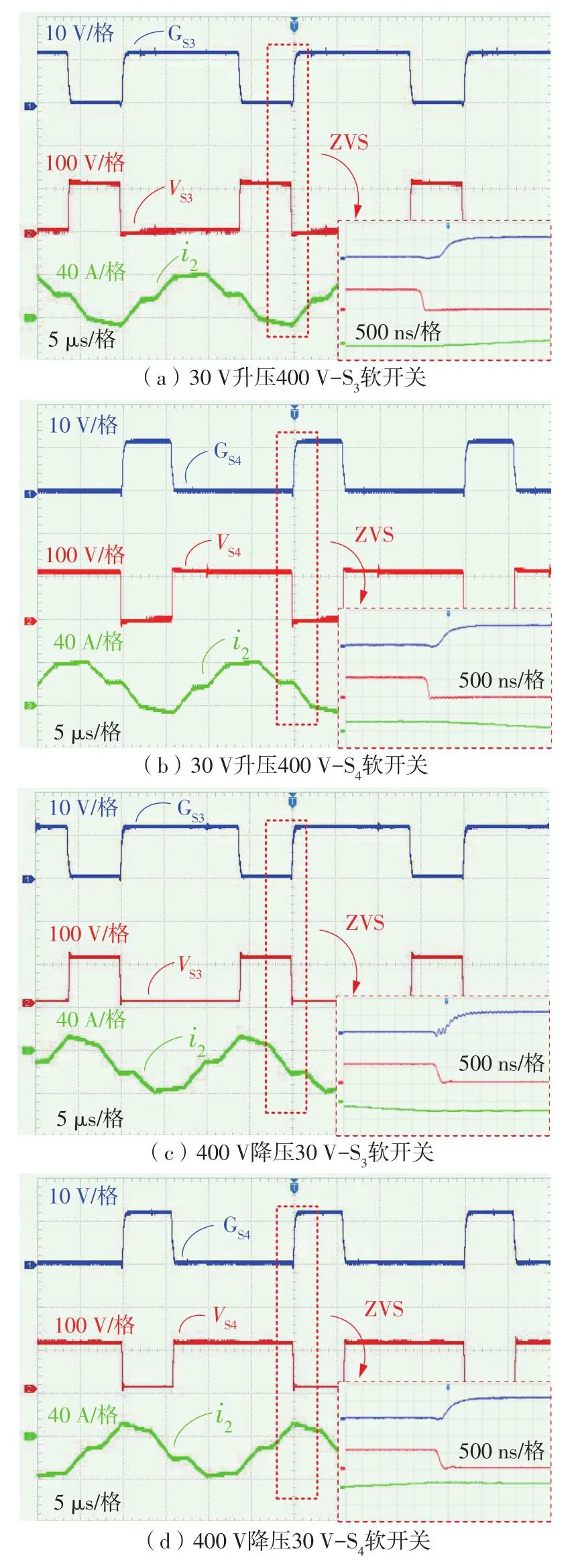
图10 额定功率下不同模式低压侧的开关管ZVSFig.10 Low-voltage side MOSFET ZVS in different modes at rated power
电流自均衡直流变换器在额定功率下软开关波形如图11所示。由于Q1(Q2)和Q4(Q3)软开关条件一致,故此处仅给出开关管Q1和Q2软开关波形。以图11(a)为例,开关管漏源极电压VQ1上升沿滞后于漏感电流ileak置零时刻,开关管实现了零电流关断。以图11(b)为例,开关管驱动信号GQ2上升沿滞后于开关管漏源极电压的下降沿,开关管实现了零电压开通。进一步,由图11可知,本变换器不论在升压模式还是降压模式,其高压侧开关管均可实现零电压开通或零电流关断,从而保证变换器的高效运行。

图11 额定功率下不同模式高压侧的开关管软开关Fig.11 Different modes of high-voltage side MOSFET soft switch at rated power
5 结论
本研究提出了一种电流自均衡的耦合电感型低电流纹波高电压增益双向直流变换器。首先介绍了本变换器的电路特性和工作原理并分析了经典的工作模态。接着详细论述了其电压增益、传输功率、软开关、电流自均衡机理与低电流纹波特性。最后,设计了一款1 kW实验样机。通过理论分析和样机实验,可以得出如下结论:
(1)本变换器通过交错耦合电感技术的使用,可以实现高电压增益、低电流纹波、软开关特性和功率双向流动的综合。
(2)本变换器通过低压侧钳位电容,无需附加测量单元和复杂控制算法,即可实现低压交错电流的自动均衡。
(3)本研究提出的自动均流方案具有良好的拓展性,只需要扩展高压侧电路或者低压侧电流通道,即可在保持均流的前提下实现更高的电压增益和更低的电流纹波。

