基于自适应阻尼的虚拟同步发电机并离网控制
卢栩舜,朱金荣,王磊
(南京工程学院电力工程学院,江苏南京 211167)
微电网一般不能直接并入电网使用,需要变流器作为接口。由于不具备传统的同步发电机的惯性和阻尼特性,高密度的可再生分布式电源导致系统的低惯性和稳定性问题尤为突出。系统在低惯量,低阻尼运行场景下,有功扰动会产生较大的频率变化[1]。
为解决以上问题,虚拟同步发电机(VSG)的概念被提出[2],该技术模拟同步发电机(SG)转子运动方程对变流器进行控制,使DG 具有与SG 类似的外特性,为系统提供惯性和阻尼,从而增强变流器自身的频率调节能力,提高系统的稳定性[3]。因此,VSG 在有功扰动发生时能够为系统提供必要的惯量支撑和功率补偿。与传统SG 相比,VSG 的输出更加平滑可控,通过修改虚拟参数可灵活调节系统阻尼,这为不同工况下的系统阻尼调控提供了技术支撑[4-5]。
文献[6]利用同步发电机的功角特性曲线及转子角速度振荡周期曲线,分析了自适应转动惯量对系统频率稳定作用机理。文献[7]基于改进型模糊自适应惯量的VSG 控制技术,能够自适应地调节转动惯量的数值,达到兼顾系统响应快速性和稳定性的目的。
上述文献仅研究了转动惯量对系统的影响,未考虑虚拟阻尼调节与系统频率稳定的关系。文献[8-11]中提出基于VSG 的惯量和阻尼自适应控制,研究自适应惯量和自适应阻尼协调控制。文献[12]详细研究了控制参数对VSG频率和功率的影响。文献[13]对不同工况运行下虚拟同步发电机的参数设计进行研究。文献[14]通过引入系统阻尼比,说明系统限制在欠阻尼状态下比较稳定。
上述所提的VSG 控制策略考虑了并网和离网两种运行模式,然而,并离网切换作为VSG 的一个重要功能,确保了即插即用的能力,在现有的工作中没有被考虑。该文提出了一种基于自适应阻尼的VSG 并离网优化控制方法,在保证VSG 实现一次频率调节、二次频率调节和电压调节的基础上建立小信号模型,分析表明在不同工况下阻尼因子的最优值不相同,设计自适应阻尼的控制方案,在并离网运行时,采用阻尼自适应调节,减小扰动引起的频率波动;在并离网切换时,自动匹配相应阻尼最优值,实现阻尼自适应切换。最后通过Matlab/Simulink 进行模型搭建和仿真验证,证实了所提策略能够保证VSG在各工况下的处于最佳性能运行,并能实现不同工况的平稳切换。
1 虚拟同步发电机控制
图1 所示为变流器结构模型,其中左侧直流电压代表微电网或RES 的直流电源,右端输出侧经LC滤波连接本地负载和并网开关。

图1 变流器模型
对变流器采用虚拟同步发电机控制可以达到等效替代同步发电机的作用。
1.1 内部电压电流控制回路
变流器交流侧电路方程在dq坐标下可表示为:
其中,ω为系统角频率;ud、uq和vd、vq为dq坐标下的变流器调制电压和交流侧输出电压;im_d、im_q和id、iq分别为dq坐标下变流器输出侧经过滤波器前后的输出电流。
内部控制回路包括电压和电流控制,dq坐标下各参数定义式如下:
其中,Kpi和Kii为电压调节系数;imref_d、imref_q为dq坐标下变流器输出电流参考值;γd、γq为dq坐标下变流器输出电流偏差积分值。
电流参考值可根据电压控制回路得到:
其中,Kpv和Kiv为电流调节系数;vref_d、vref_q为dq坐标下交流侧输出电压参考值;φd、φq为dq坐标下交流输出电压偏差积分值。
1.2 VSG控制原理
同步发电机的转子方程如下:
其中,H为系统等值惯性常数;Pm_pu、Pe_pu为机械功率和电磁功率标幺值;ωm、ωpll为机械角频率和交流侧输出电压角频率;D为转子阻尼系数;θm为机械相位角。
由式(9)可得控制框图,如图2 所示。
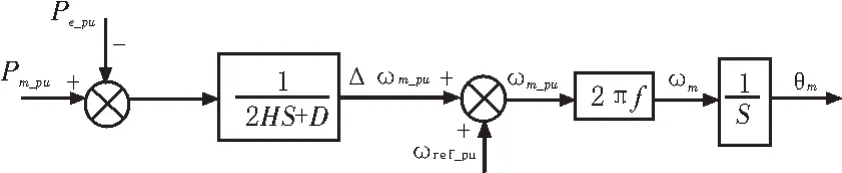
图2 VSG控制模型
为满足频率调节要求,P-f控制如式(10)所示。
其中,Pref和ωref为有功参考值和角频率参考值;Kpf和Kif分别为功率一调系数和功率二调系数;ζ为角频率偏差积分值。
为满足电压调节要求,Q-V 控制如式(11)所示。
其中,E为额定电压有效值;mQ为无功下垂系数;Qref和Qf为无功参考值和交流侧输出无功。
锁相环用于测量公共连接点(PCC)频率,其控制环节如式(12)-(14)所示。
其中,ωN为系统额定角频率;Kp_pll和Ki_pll为频率调节系数;εpll为电压积分值;δωpll为交流侧输出角频率和系统额定角频率的差值;θpll为交流侧输出电压相角。
2 线性化小信号状态空间模型
系统的小信号状态空间模型(x’=Ax+Bu)可由非线性模型线性化得到[15],如表1 所示为所提模型及控制回路参数。
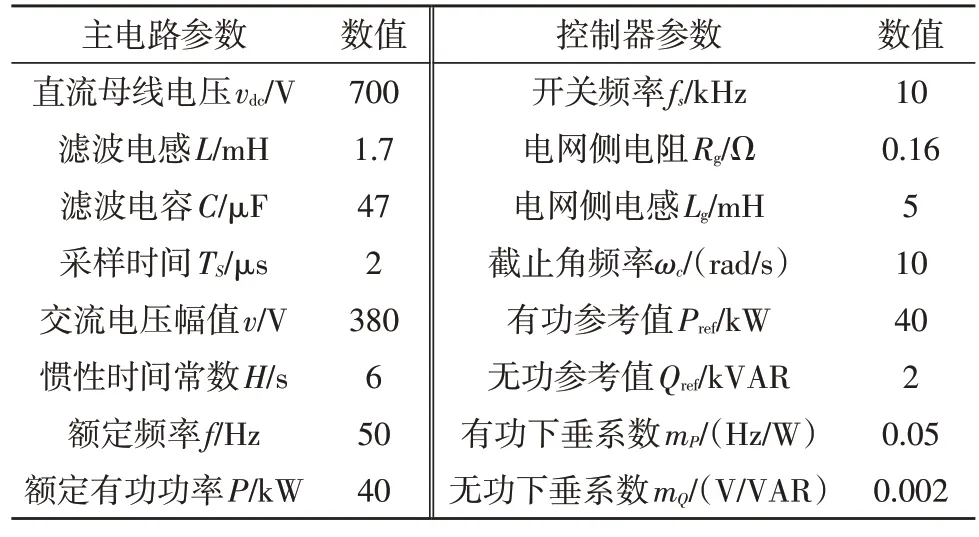
表1 仿真模型参数
2.1 离网模式
离网工作模式下,VSG 模型的状态变量如式(15)所示,得到15 阶状态空间方程。
线性化的状态空间模型用于分析VSG 控制在离网运行模式下的状态。计算当阻尼因子D=2 时,A矩阵的特征值,如表2 所示,系统15 种状态下的特征值都位于虚轴左侧,显示了系统的稳定性。

表2 离网模式下系统特征值
为确定离网运行时阻尼因子的最优值,将D从0增大到无穷时的根轨迹如图3 所示。
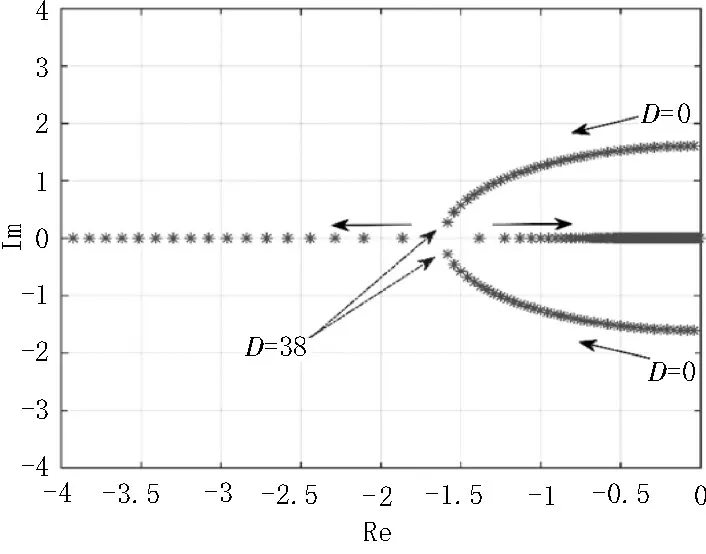
图3 离网模式下不同D下的有功环根轨迹
从图中可以看出,随着D的增大,首先稳定度增大,根轨迹同时向负半轴移动,此时系统动态性能较好,系统处于欠阻尼状态,有一定超调,随着D的继续增大,系统逐渐达到临界阻尼状态,如果D继续增大,轨迹逐渐在实轴会合,并沿相反方向运动,系统进入过阻尼状态,会导致系统调节时间增加。离网模式下,D=38 为欠阻尼临界值,D>38 时系统呈临界阻尼响应,故该模式下阻尼最优值为D1=38。
2.2 并网模式
离网工作模式下,VSG 模型的状态变量如式(16)所示,得到16 阶状态空间方程。
线性化的状态空间模型用于分析VSG 控制在离网运行模式下的状态。计算D=100 时,A矩阵的特征值,如表3 所示,系统16 种状态下的特征值都位于虚轴左侧,显示了系统的稳定性。
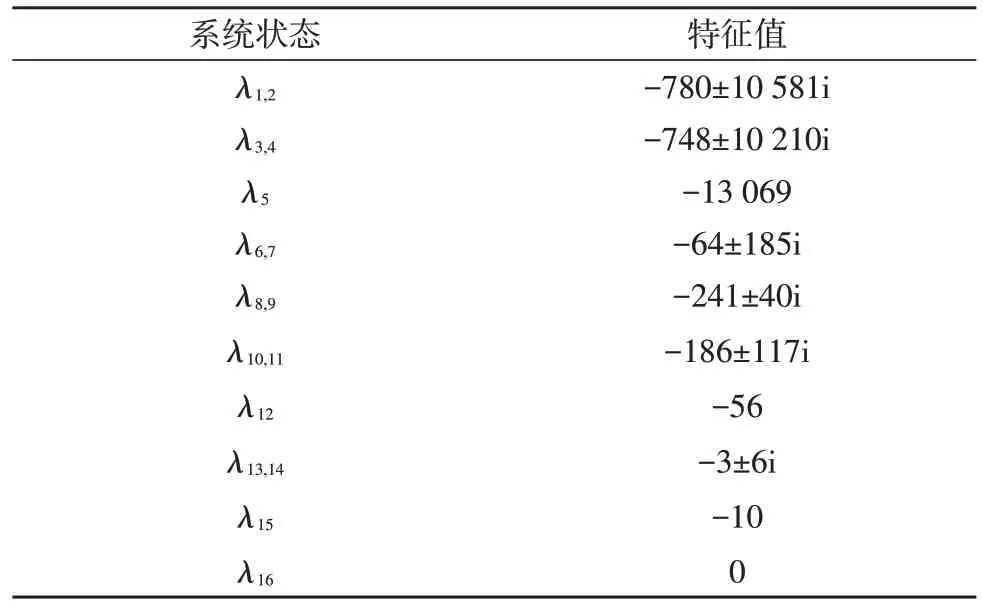
表3 并网模式下系统特征值
为了确定并网运行时阻尼因子的最优值,将D从0 增大到无穷时的根轨迹如图4 所示。

图4 并网模式下不同D下的有功环根轨迹
同理,在并网模式下,D=183 为欠阻尼临界值,D>183 时系统呈临界阻尼响应,故该模式下阻尼最优值为D2=183。
3 自适应阻尼控制
该文提出的基于自适应阻尼的VSG 控制方案如图5 所示。

图5 自适应阻尼下的VSG控制框图
3.1 阻尼自适应调节
当VSG 在并网条件下发生功率扰动时,功率与系统频率都会在扰动的瞬间出现衰减振荡,而振荡的超调量与趋于稳定的时间是评判系统稳定性的关键参数,文献[16]中的调节原则如表4 所示。

表4 阻尼自适应调节原则
3.2 阻尼自适应切换
由于并离网两种模式下VSG 阻尼的最优值相差较大,在运行模式改变时,需进行阻尼自适应切换,如图6 所示。

图6 阻尼自适应切换
并网时选用D1,离网时选用D2,可以减小VSG 与电网同步时的频率振荡,使得切换过程平滑。
4 仿真试验与分析
为验证所提策略的正确性和有效性,利用Matlab/Simulink 进行仿真,其结果表明了所提控制策略在孤岛和并网运行模式下的性能以及并离网切换中对频率稳定性的影响。
4.1 并离网特性
在VSG 并网模式和离网模式下,有功负载增加时,参与系统的一次调频和二次调频并实现阻尼自适应调节,如图7 所示。

图7 不同策略下有功负载增加时的频率变化
图中开始时,本地有功负载为36 kW,在t=16 s时,达到额定有功功率40 kW,负载瞬间增加4 kW,由于VSG 的二调作用,两模式下频率在经过波动之后均稳定于50 Hz。相较于传统策略,所提策略在不增加调节时间的情况下,波动更小。
4.2 并离网切换
VSG处于离网运行模式,本地有功负载为36 kW。并网指令发出后,系统开始启动电压预同步控制,两电压完全同步且为过零点,并网开关闭合,完成VSG离网转并网切换,交流侧输出电压波形与电网电压波形如图8 所示。
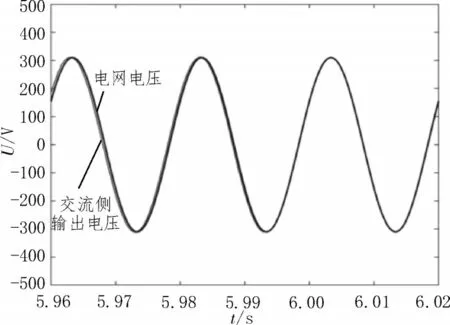
图8 并离网切换前后波形对比
6 s 时并网开关闭合,VSG 完成离网转并网切换;12 s时并网开关断开,VSG完成并网转离网切换。切换前后不同控制策略下的频率波形变化如图9所示。

图9 并离网切换前后频率对比
将传统策略与所提策略进行对比,传统策略下,VSG 运行模式改变会由于自身阻尼恒定而导致系统呈欠阻尼或过阻尼响应,并网时频率振荡明显,离网时频率恢复时间过长。所提策略根据VSG 运行模式的改变,阻尼自适应切换为相应最优值,频率不会出现超调现象,并且可以很好地适应工作模式的切换。
5 结束语
该文以虚拟同步发电机技术下的变流器为研究对象,建立其离网模式和并网模式下的小信号模型,验证了不同工况下VSG 控制方案的稳定性,得出不同工况下的阻尼最优值不同并找出离网和并网模式相应的阻尼最优值。在此基础上,提出了基于阻尼自适应的VSG 并离网控制方案,在并离网运行时,采用阻尼自适应调节,减小扰动下的频率波动;在并离网切换时,自动匹配相应阻尼最优值,实现阻尼自适应切换。最后,通过仿真验证,相比于传统控制策略,该方法可有效提高VSG 并离网运行时的调频特性和抗干扰能力,抑制并离网切换时的系统振荡,提高系统的频率稳定性。

