基于IUPLCD与DTBSVM的输气管道泄漏检测方法

刘 勇,吴明畅,徐 航,李洪伟

(1.国家石油天然气管网集团有限公司西气东输分公司,上海 200120;2.沈阳国仪检测技术有限公司,辽宁沈阳 110041)

0 引言

管道运输是油气等能源的主要运输方式之一,这种运输方式成本低,损耗低。油气管道沿线比较复杂,大多铺设在野外或偏远的地方,铺设环境比较恶劣。所以,管道极易出现油气泄漏的现象。天然气具有易燃、易爆性[1-2],所以一旦泄漏,可能会引起爆炸等事故。因此,对管道进行泄漏检测是管道运行管理中的一项重要工作[3-4]。

目前,对管道进行泄漏检测的方法很多。根据当前应用的情况,可以分为非声学的检测方法和声学检测方法[5]。声学法具有检测精度高、误报率低等优点。但是,声波在传播的过程中极易受到环境的干扰,使得声波信号中含有大量噪声,从而降低泄漏的识别准确性。因此,对声波信号进行去噪尤为重要。Q.Meng等[6]提出了一种EEMD和互谱分析相结合的去噪方法,可以有效降低噪声含量。X.M.Lang等[7]对LMD去噪方法进行改进,改进后可以准确得出与泄漏信号相关的生产函数,但去噪后的信号中仍有残余噪声。TWSVM是最经典的分类方法之一,但它处理多分类问题时存在不足[8]。TBSVM是在TWSVM基础上改进而来,与TWSVM相比,它具有更快的训练速度和更高的精度[9]。B.P.Zhou等[10]采用深度神经网络来识别管道的泄漏,该方法取得的效果明显优于传统泄漏检测方法。Z.Y.Liao等[11]将深度学习和TFR结构相结合,实现对管道工况的识别,但该方法运算速度较慢,准确率较低。

因此,为了提高泄漏的识别准确率,本文提出了一种基于IUPLCD与DTBSVM的管道泄漏检测方法,能够准确识别输气管道的泄漏,有效地减少了系统的漏报和误报。

1 基本原理

1.1 匀相窄波局部特征尺度分解

与经验模态分解EMD相比,局部特征尺度分解(LCD)在性能上得到了更好的改进,它能够有效减小包络拟合误差以及端点效应[12]。但是,LCD并不能完全消除模态混叠现象。UPLCD通过在需要分解的信号中加入相位均匀变化的窄带余弦信号,将得到的各个极值点的分布均匀化,进而达到消除模态混叠的效果[13]。UPLCD的分解步骤如下:

(1)计算分解算法的循环周期Tc以及次数nisc

nisc=log2(l)

(1)

Tc=2m

(2)

式中:l为数据的长度;m是循环次数的倒数,m=1/nisc。

根据信号的实际情况,对幅值ε的数值和相位的个数np进行设置。

(2)令x(t)=r0(t),w(t,εc,fc,θk)为窄波余弦信号,可得:

w(t,εc,fc,θk)=εc·cos(2π·fc·t+θk)

(3)

εc=ε·rm-1(t)

(4)

θk=2π(k-1)/np

(5)

式中:rm-1(t)为标准偏差;θk是信号的相位;fc为余弦信号的频率;εc为幅值和标准偏差的乘积。

(3)将LCD分解得到的第i个ISC分量用Li(·)表示,LCD分解得到的第1个分量为:

cm,k(t)=L1[x(t)+w(t,εc,fc,θk)],k=1,2,…,np

(6)

(7)

式中:cm,k(t)为加入窄波余弦信号后构造的待分解信号;ISC1为第一个ISC分量。

(4)从源信号x(t)中减去得到的ISC1分量,将剩下的信号作为新的源信号ri(t),重复以上步骤,得到所有的ISC分量,直到分解出所有的ISC分量后,停止循环,rnisc(t)为残余项。

1.2 改进匀相窄波局部特征尺度分解

UPLCD虽然比LCD的性能改善了很多,但是在信号的重构规则上并未变化,仍然和LCD一样,没有制定一个信号的重构原则,是将所有的ISC分量用于信号的重构,这样就会导致一些包含噪声较多的ISC分量也用于重构,造成重构信号中仍含有部分噪声。本文采用ISC分量的能量和傅里叶频谱分析后的幅值标准差作为ICS的选择标准,从所有的ISC分量中将包含有用信息更多的分量筛选出来。

ISC分量中,既包含有用信息,也包含无用信息(噪声信号)。噪声信息占比大的ISC分量称为噪声主导分量,有用信号占比大的ISC分量称为信号主导分量。ISC分量的能量曲线中,第一个极值点是区分ISC分量是受噪声还是有用信号支配的临界点[14],即能量曲线临界点之前(包括临界点处)的所有分量均为噪声主导的分量,临界点之后的分量为信号主导的分量。ISC分量的能量可以由以下公式求得:

(8)

式中:ei为第i个ISC分量的能量;M为序列的长度。

标准差(STD)是方差的算数平方根,它能反映一个数据集的离散程度,而且相较于方差,标准差能够直观地反应出数据集的偏离程度[15]。对信号进行UPLCD分解后得到的若干个ISC分量进行傅里叶变换,得到的频谱图中,无用信号多的频谱图与有用信号多的频谱图相比更加复杂。此时,可以用标准差对数据集的离散程度进行度量。包含有用信息多的数据,其标准差较小,包含无用信息多的数据集,其标准差明显高于有用信息多的标准差。因此,可以采用标准差来筛选出包含泄漏信息多的ISC分量。

标准差的计算公式如下:

(9)

由于UPLCD没有给出合理的ISC分量的筛选原则,所以本文通过制定一个筛选准则来对其进行优化改进,筛选出有效ISC分量。具体流程如图1所示。

图1 降噪流程图

IUPEMD的具体步骤如下:

(1)对原始信号进行UPLCD分解,得到若干个ISC分量;

(2)分别计算各个ISC分量的能量,确定能量曲线的第一个极值点;

(3)对各个ISC分量进行傅里叶变换,然后对每个ISC分量的幅值进行归一化处理,再求得其标准差;

(4)根据ISC分量的能量值和幅值的标准差筛选出信号主导的ISC分量,并将同时满足以上2个条件的ISC分量用于信号的重构。

1.3 深度孪生有界支持向量机

与TWSVM相同,TBSVM也是采用寻找2个非平行的决策超平面实现对输入数据的分类判断。线性TBSVM的优化问题如下[16]:

(10)

限制条件:

(11)

(12)

限制条件:

(13)

由式(10)～式(13)可得,一个目标函数的约束由另一个目标函数的模式确定,2个超平面互相限制。线性状态下,TBSVM的拉格朗日对偶式为:

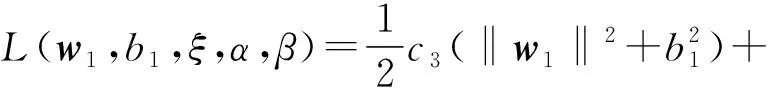
(14)

式中α,β均为非负的拉格朗日乘子。

综上,可以得到线性条件下,为了线性规划问题能有最优解,由KKT条件可得对偶问题为:

(15)

(16)

式中:P和N均为优化问题的最优值;0≤α≤c1;G、H为数值矩阵;G=[B,e2];H=[A,e1];γ为拉格朗日乘子,0≤γ≤c;I为合适维度的单位矩阵。

此时,当有待判定新样本输入时,线性TBSVM可以根据下式判断样本所属标签。

(17)

式中:Classi为类别;wk和bk分别为权向量、偏差。

当数据在低维空间线性不可分时,SVM利用核函数将其映射到高维空间,再对数据进行分类。和SVM的处理方法相同,TBSVM也是采用核函数对数据进行映射,再利用在线性条件下的方法对数据进行分类。引入核函数后,TBSVM的2个超平面可以表示为:

(18)

式中:K表示核函数;C=[A,B]T;u是高维空间中的非线性数据。

非线性TBSVM的优化问题如下:

(19)

限制条件:

(20)

(21)

限制条件:

(22)

定义:

S=[K(A,CT)e1]
R=[K(B,CT)e2]

(23)

此时,可得TBSVM对应的朗格朗日对偶问题为:

(24)

(25)

式中:0≤α≤c1;0≤γ≤c2;P和N均为优化问题的最优值。

此时,当有待判定新样本输入时,非线性TBSVM可以根据下式判断样本所属标签。

(26)

TBSVM是TWSVM的改进,它使用逐次超松弛技术,使训练速度更快。此外,TBSVM采用了结构风险最小化原则,与TWSVM相比,TBSVM的分类精度更高,计算时间更少。深度学习是机器学习中最重要的一个分支,它通过训练多层的网络结构实现对数据集的分类或者回归[17]。深度学习不需要提取特征,而是自动对数据进行筛选、提取特征[18]。在深度学习和TBSVM的基础上,结合两者的优点,组建了一种新的网络模型DTBSVM。

DTBSVM是一个3层网络模型。输入层输入管道两端传感器测得的数据。隐含层的3个TBSVM通过生成6个超平面将数据映射到六维空间,实现特征的提取。这3个TBSVM之间的唯一的区别是参数的不同。输出层中包含一个TBSVM,用于分类。本模型不仅充分发挥了DL和TBSVM的优点,还克服了浅层模型的不足,具有良好的准确性。DTBSVM的模型如图2所示。

图2 DTBSVM模型

Ci1,Ci2(i=1,2,3)分别为隐含层中3个TBSVM的参数,本文采用交叉验证和网格搜索的方法来确定其最优值。管道泄漏时,传感器采集的数据基本上为非线性数据,而径向基函数(radial basis function)具有良好的非线性映射能力、泛化能力,所以,在非线性情况下,本文采用RBF核函数K(xi,yi)=exp(-λ‖xi-xj‖2)。

无论是在线性情况下还是非线性情况下,隐含层中的每一个TBSVM都会生成1对超平面。隐含层中TBSVM生成的6个超平面可以将传感器采集的原始数据投射到六维空间中,得到原始数据的六维位置信息,进而提取数据的特征,生成1个新的特征数据集。输出层的主TBSVM根据特征数据集对管道的状态进行识别。

模型的训练可以分为2步:首先,采用非监督学习的方式对模型的每一层进行训练,调整各层的各项参数。训练时,前一层的输出作为后一层的输入,直到每一层都训练完成。在第1步的基础上,采用监督学习对模型各个层的参数进行调整,使得各层参数到达最优值,进而将误差最小化。

2 实验

本文采用某石化公司的输气管道进行了泄漏实验。管道长度12 km,管径为200 mm,管道首末端的压力分别为2.3 MPa和0.6 MPa。在管道的1、3、5、7、11 km处各有一个口径为8 mm和5 mm的球阀。管道首末端各安装一个PCB 106B型声压传感器,用来采集管道内的超声波信号,其量程为0～57 kPa,灵敏度为43.5 MV/kPa,采样频率设为1 000 Hz。数据采集装置采用的是NI-DAQ9181数据采集器,对数据进行采集。实验原理图如图3所示。

图3 实验原理图

以传感器1采集到的超声波信号为例,进行去噪实验。打开管道3 km处的8 mm阀门,模拟管道出现泄漏,传感器1在管道首站采集的原始信号如图4所示。

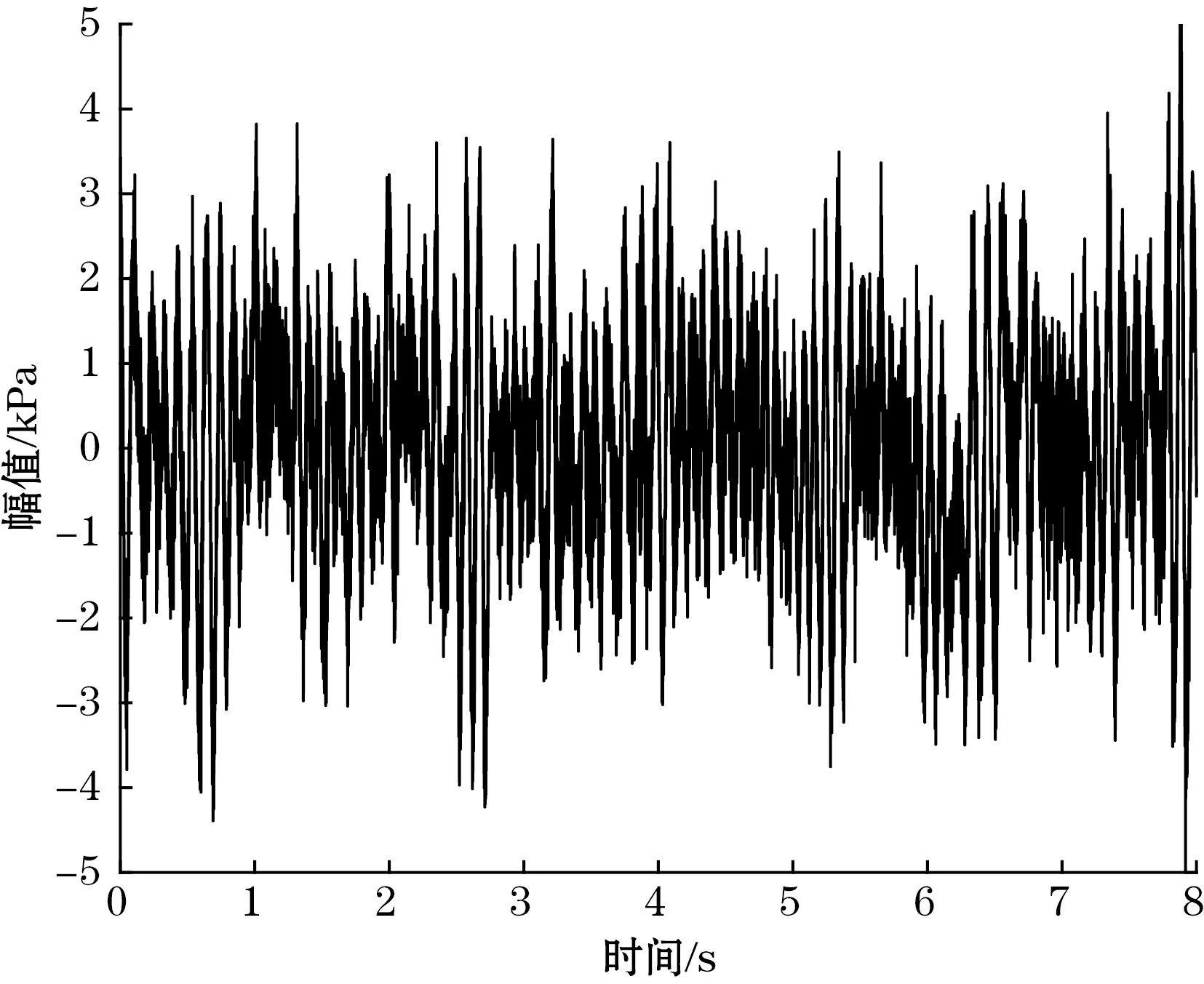
图4 去噪前的超声波信号曲线

从图4中可以看出,原始信号含有较多的噪声,信号波动较大,无法判断信号曲线的变化趋势。现采用IUPLCD算法对原始信号进行降噪处理。首先,采用UPLCD算法对原始信号进行分解,将原始信号分解为12个不同尺度的ISC分量和1个残余项。然后计算各个ISC分量的能量值和分量FFT变换后的幅值的标准差。最后根据能量值和标准差对ISC分量进行筛选并进行信号重构。ISC分量的能量曲线中,第1个极值点是区分ISC分量是受噪声还是有用信号支配的临界点,也就是说能量曲线临界点之前(包括临界点处)的所有分量均为噪声主导的分量,临界点之后的分量为信号主导的分量。图5为各ISC分量的能量值。

图5 各ISC分量的能量值

从图5中可以看出,能量曲线的第一个极值点为ISC4所对应的点。因此,ISC1～ISC4为噪声主导的分量,ISC5～ISC12为信号主导的分量。

对UPLCD分解得到的各个ISC分量进行傅里叶变换,得到的频谱图差别较大,离散程度不同。噪声主导的ISC分量的频谱图,其复杂程度更大。标准差能反映一个数据集的离散程度,而且相较于方差,标准差能够直观地反映出数据集的偏离程度。因此,可以采用标准差来判断哪些分量为信号主导的分量。为了防止傅里叶变换后不同阶的ISC分量的幅值的数量级不同,本文先对数值进行归一化处理,再计算不同ISC分量之间的标准差。图6为各ISC分量傅里叶变换后幅值的标准差。

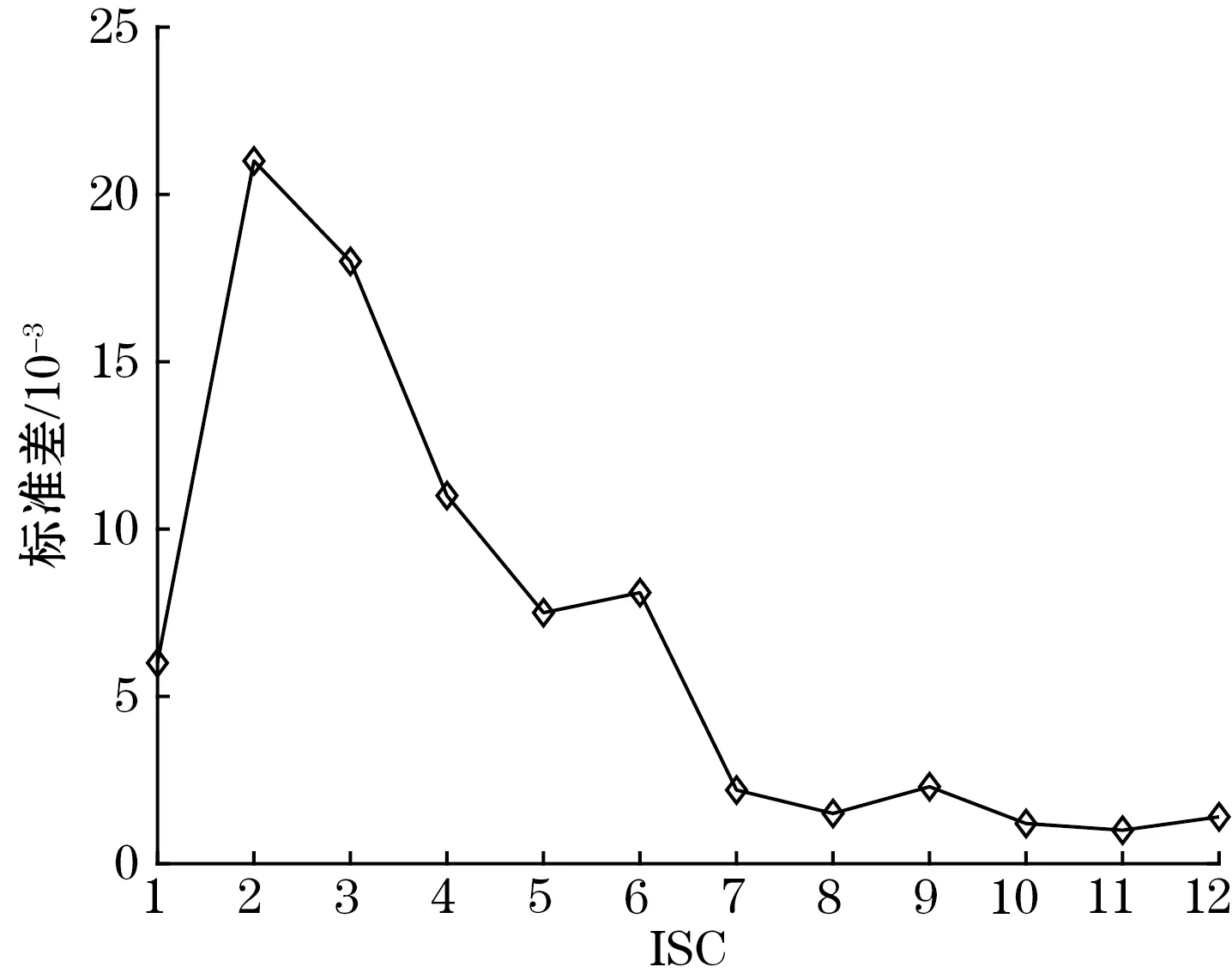
图6 各ISC对应的幅值的标准差

由图6可得,ISC1～ISC6的标准差变化程度大,离散程度高,所以为噪声主导的分量。ISC7～ISC12的标准差变换程度较小,而且离散程度低,所以ISC7～ISC12为信号主导的分量。

为了能够最大程度地保留原始信息,本文将同时符合能量值和标准差要求的ISC分量用于信号的重构。综合ISC分量的能量曲线以及幅值标准差曲线,ISC7～ISC12能够同时满足以上2个要求,所以选择ISC7～ISC12用于信号的重构。在同样的条件下,选用UPLCD对信号进行去噪处理,将其得到的信号曲线与IUPLCD去噪后的信号曲线进行对比,如图7、图8所示。

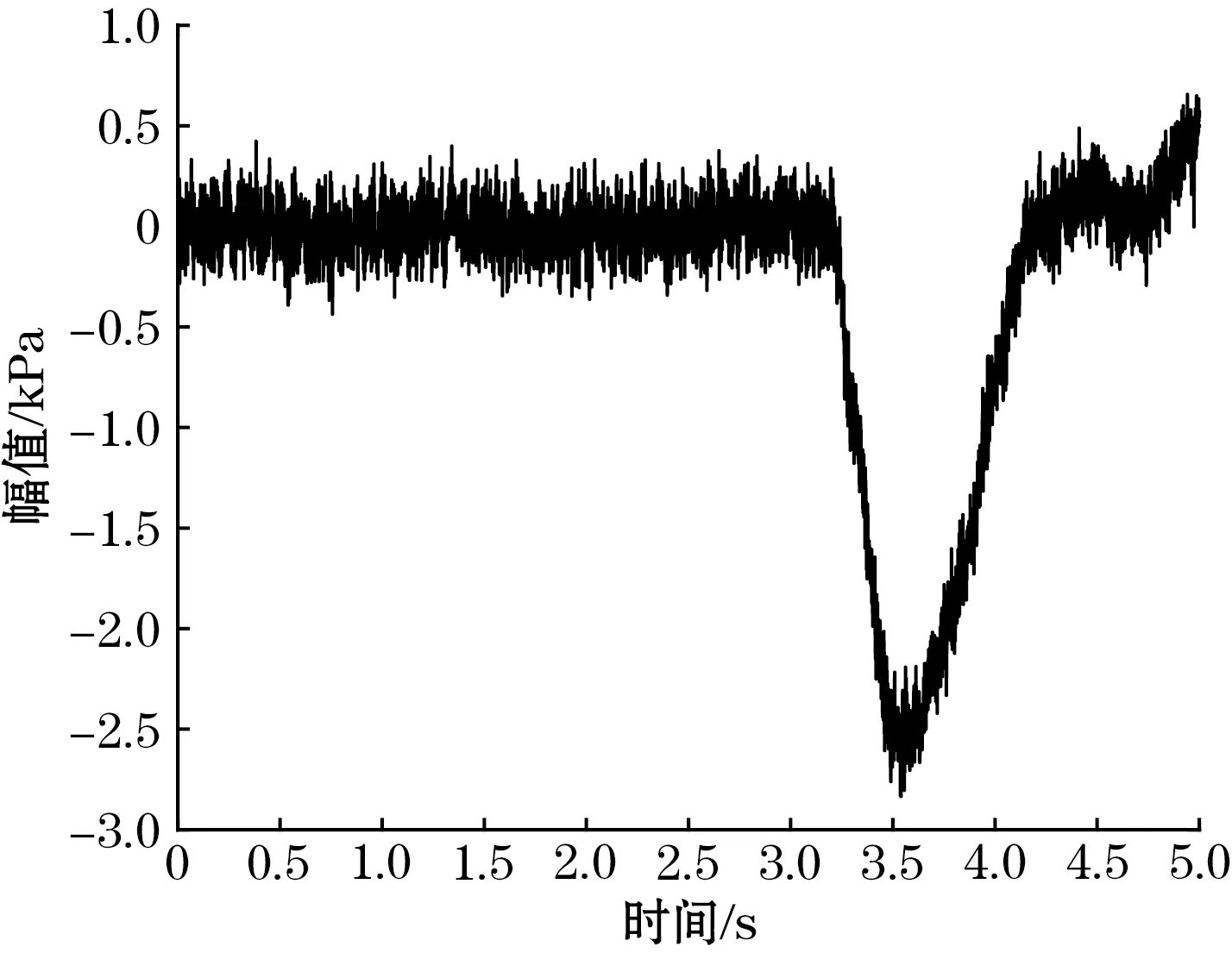
图7 UPLCD去噪后的信号曲线

从图7～图8中可以明显看出,采用本文方法得到的曲线更加平滑,含噪声更少,最大程度地保留了原始泄漏信息,可以明显地看出信号的变化趋势以及拐点。

在管道1、3、5、7、11 km处分别打开8 mm和5 mm的阀门模拟泄漏,并各采集3 000组泄漏声波信号。在管道正常工况下,同样采集3 000组数据。为了提升判断准确性,采用IUPLCD算法对上述信号进行去噪。

线性情况下,隐含层中3个TBSVM的参数取值为:c11=0.32,c12=0.13,c21=c22=0.25。c31=0.3,c32=0.2。输出层TBSVM的参数c1=c2=1。非线性情况下,c11=0.1,c12=0.32,c21=c31=0.3,c22=c32=0.1。输出层TBSVM的参数c1=1,c2=10。隐含层中3个TBSVM均采用RBF核函数,且参数λ的取值分别为1、0.1、0.1。

将经过降噪处理后的前2 000组数据作为训练数据集,对DTBSVM模型进行训练,得到各项参数的最优值。训练完成后,将剩余的1 000组数据作为DTBSVM的输入,对管道的工况进行识别。在相同的条件下,使用相同的数据,采用TWSVM和TBSVM对管道工况进行识别,并将识别结果进行对比,本文定义识别精度=(正确数目/总数)×100%,对比结果如表1所示。

表1 不同模型的识别精度对比

根据表1可得,不论是不同位置的泄漏,还是同一位置不同大小的泄漏,DTBSVM对管道泄漏的识别准确性明显要高于TWSVM和TBSVM模型的准确性,DTBSVM对管道泄漏的识别精度最高可达99.7%。

3 结束语

为了能够准确、及时的识别管道的泄漏,防止出现安全事故,本文提出了一种基于IUPLCD和DTBSVM的管道泄漏检测方法。首先,针对UPLCD算法无法选取有效ISC分量的缺点,本文对算法进行了优化改进。将ISC分量的能量值和傅里叶变换后的幅值的标准差作为有效ISC分量的筛选标准,筛选出信号主导的ISC分量,并将其用于信号的重构。重构后的信号中,噪声含量极低,更好地还原了原始泄漏信号。最后,为了准确、及时的识别出管道的泄漏,本文根据深度学习与TBSVM的优点,构建了一种新的管道泄漏识别模型DTBSVM。经现场实验验证,将降噪后的信号输入到DTBSVM模型中,可以准确判断出管道的工况,且识别准确率高,有效地降低了系统的漏报率和误报率,为智慧管网的建设和管理提供了便捷和参考。