大型浮体水动力响应特性数值模拟及减摇措施

何良德,黄 挺,李俊龙,罗成未

(1.河海大学港口海岸与近海工程学院,江苏 南京 210098; 2.长江勘测规划设计研究有限责任公司,湖北 武汉 430015)

随着全球人口数量膨胀和陆地资源紧张,海洋空间的开发利用成为一个必然趋势。近年来,以大型浮体为组建单元的漂浮城市、浮式人工岛等概念被相继提出,成为研究热点[1-3]。通常,大型浮体既可以作为独立的海洋平台使用,也可以作为单元模块拼接组成超大型浮体[4-5]。大型浮体在波浪下会产生明显的摇荡运动[6-8],严重时不仅会影响浮体上设备、人员的正常工作,甚至还会发生倾覆事故。因此,关注大型浮体的水动力响应具有重要意义。

目前,大型浮体主要有半潜式和浮箱式2种[9],李良碧等[10]采用Sesam软件对半潜式大型浮体进行水动力分析,结果表明横向浮筒半潜式大型浮体纵荡幅值比纵向浮筒型小很多;袁杨[11]对半潜式大型浮体五浮筒型以及三浮筒型2种方案进行了频域下的水动力性能分析,发现五浮筒方案水动力性能更优;王亚香等[12]基于物理模型试验,研究了浮箱式浮体在波浪场中的动力响应,发现浮体纵荡和纵摇均随相对波高增大而增大,随相对板长的增大而减小;舒志等[13]应用三维水弹性理论和刚体的三维势流理论,对比研究了浮箱式超大型浮式结构物在波浪中无系泊时的运动响应,发现浮体前三阶垂向弯曲传递函数的响应幅值与结构的升沉运动幅值相当。已有工程经验表明,浮箱式浮体构造简单,拼接容易,是近海海洋载体的优选形式,但因水线面面积大,波浪作用下运动响应问题十分突出[14-15],有必要开展浮箱式大型浮体水动力响应的控制研究。

本文以马尔代夫海域作为潜在的工程应用背景,研究大型浮体的选型、水动力响应及减摇问题。考虑到现有施工技术条件下单个大型浮体尺寸有限,结构的水弹性变形不显著[16],故本文简化认为浮体为刚体,其响应采用刚体运动方程进行计算。在此基础上,采用三维势流理论考虑水动力荷载作用,研究浮箱式浮体波浪响应特性以及减摇板布置方式和形式对水动力响应的控制效果。

1 大型浮体工程简况

大型浮体工程拟选址于马尔代夫首都马累附近的芭环礁内。该海域平均水深50m,流速、风速较小,因此浮体水动力响应主要受波浪的影响。根据观测数据,芭环礁外海波浪常浪向为SSW,2年一遇有义波高为3.3m,谱峰周期为8.3s,100年一遇有义波高为4.6m,谱峰周期为10.2s。主风向为W,平均风速为4.7m/s。由于芭环礁海域海况相对平静,水深较浅,大型浮箱式浮体是合理的选择。

2 浮体运动计算理论

本文采用数值模拟软件AQWA进行建模并开展水动力响应计算。

2.1 势流理论

势流理论假定流体为无黏、无旋、不可压缩的理想流体,即存在速度势函数φ(x,y,z,t)。制约流体的基本方程为拉普拉斯方程(式(1))和拉格朗日方程(式(2))。

∇2φ(x,y,z,t)=0

(1)

(2)

式中:p为压力;ρ为流体密度;g为重力加速度;v为流速;C(t)为待定时间t的函数,需根据问题给出的条件决定。

拉普拉斯方程决定流场中的速度分布,拉格朗日方程决定流场中的压力分布,从而确定浮体所受到的流体作用力。对于有大尺度浮体(浮体特征长度大于1/6波浪波长)干扰的简谐传播波浪场,根据Haskind的理论,速度势函数为

φ(x,y,z,t)=φω+φd+φr

(3)

式中:φω为未经浮体扰动的入射波势;φd为固定浮体对入射波流场的干扰,称为绕射波势;φr为浮体强迫振动对静水流场的干扰,称为辐射波势。速度势函数除需满足式(1)以外,还需满足相关边界条件,包括物面条件、自由表面条件、海底条件、无穷远处条件:

(4)

式中:νbn为浮体湿表面的法向速度;S为水线面面积;Sb为浮体湿表面面积;R为流场半径;h为水平面到海底的距离。

当浮体特征长度大于1/6波浪波长时,根据速度势,通过拉格朗日积分可以求得整个流场的压力分布。流体施加在单模块上的作用力也可以进一步被求出:

(5)

2.2 莫里森方程

波浪对小尺度结构物的作用主要为黏滞效应和附加质量效应,小尺度结构物的波浪力Fw可以采用莫里森方程[17]计算:

(6)

式中:D为杆件的特征直径;Cd为阻力系数;uf为垂直杆件方向的流体质点速度;us为垂直杆件方向结构自身的运动速度;A为杆件截面面积;Cm为惯性力系数。

2.3 浮体运动方程

由式(5)可求得整个模块波浪压力分布,压力沿浮体湿表面积分即可得到浮体受到的环境外力。当浮体投影横截面尺度小于1/5波浪波长时,浮体环境外力可根据莫里森方程(式(6))计算。进一步地,可以建立运动方程:

(7)

式中:X为浮体各自由度运动响应;M为浮体质量矩阵;A为附加质量矩阵;B为辐射阻尼矩阵;Κ为静水刚度矩阵;FD为浮体环境外力,由风、浪、流荷载组成,本研究仅考虑由式(5)或式(6)计算得到的波浪荷载。采用数值方法对式(7)进行求解即可得到浮体在波浪场中的运动响应。

3 浮体选型及水动力响应特性

3.1 浮箱式浮体关键设计参数及数值模型

浮箱式浮体结构设计主要涉及的尺寸参数有长、宽、型深和干舷高度,如图1所示。参考现有工程施工能力,浮箱面积拟定为7000m2。根据工程设计要求,浮箱上部荷载为14.7kPa(包括建筑自重和活荷载,吃水约1.5m),经过试算满载吃水拟定为3m(自重吃水约1m),结构型深为6m。满载吃水线与上层甲板的距离为3m,符合《国际载重线公约》(ILLC)和《船舶与海上设施法定检验规则》关于干舷高度的要求。

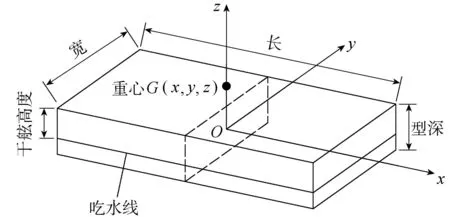
图1 浮体主要尺度参数示意图

浮箱长、宽尺寸选择涉及不同的纵横比,合理的纵横比选择应使浮箱具有较小的运动响应。由式(4)(7)可知,浮体在波浪场的运动响应与浮体湿表面形状有关。建立了4种水动力面元模型(图2),纵横比分别为1∶1(长85m、宽85m)、2∶1(长120m、宽60m)、3∶1(长147m、宽49m)以及4∶1(长172m、宽43m)。模型网格基本尺寸为1m,满足单波长能覆盖7个以上单元的要求。根据浮箱上部设计荷载以及工程应用背景,数值模拟中浮箱总重心高度设定在坐标(0,0,6)处,吃水线位于z=0m处。

图2 浮箱面元模型

实际海域中波浪是不规则的[18],由波浪引起的浮体响应是一个随机过程。通常认为不规则波由许多不同频率、波幅和相位的规则波组成,计算规则波作用下的浮箱响应是研究其复杂海况下水动力响应的基础。现采用响应幅值算子RAO(浮体响应幅值与规则波波幅的比)体现线性波浪作用下浮体的运动响应特性。不同形状浮体在0°(x轴向)和90°(y轴向)浪向下的RAO如图3所示。显然浮箱纵横比对其水动力响应影响明显,基于所依托工程浪向较为集中以及短轴向耐波性考虑,推荐采用纵横比2∶1的布置方案。

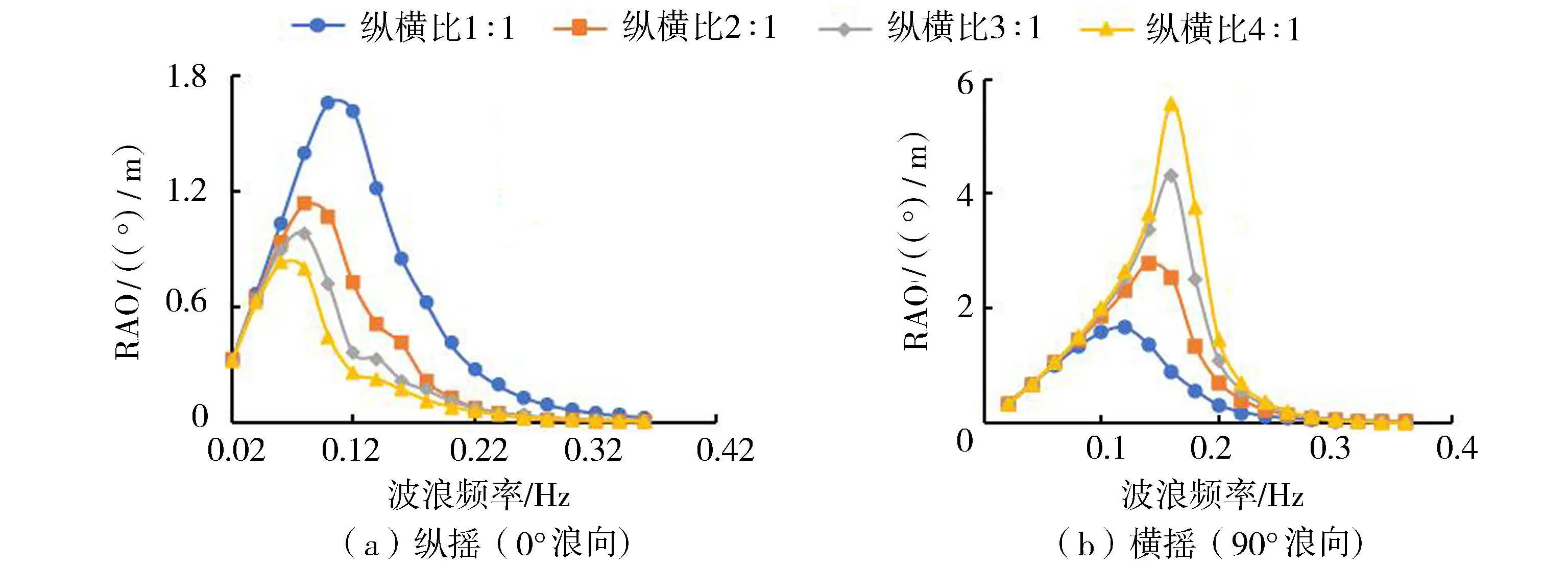
图3 纵横比对浮箱运动响应的影响

3.2 浮箱水动力响应计算结果

图4给出了纵横比2∶1浮箱6个方向自由度随波浪入射方向的变化情况。浮箱的纵荡和横荡运动呈现低频特性,在0～0.16Hz的频率区间内,运动响应随频率增大而显著减少,直至趋近于0。垂荡运动表现出类似的变化特征。低频波浪下水质点往复移动范围较大,带动浮箱产生显著的3个方向的位移。各浪向下垂荡RAO差异主要出现在0.02～0.3Hz区间,随波浪入射角转向垂直于纵轴,浮箱底部同时承受同相位波浪作用的面积增大,放大了垂荡RAO响应。横摇和纵摇RAO在计算频率范围内均是先增大后减小,与浮箱自身频率(0.1Hz)相关。相比较而言,横摇响应整体较纵摇明显,在工程应用中应加以注意。艏摇响应在45°时最显著,随波浪频率呈下降趋势。图4表明,不同迎浪面时浮箱主导运动响应不同,对于浪向集中的海域应注意合理选择布置方向。

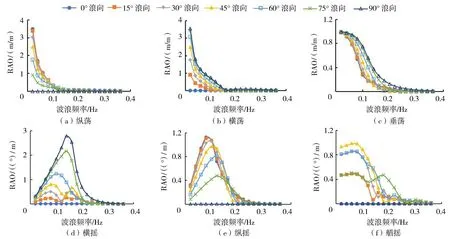
图4 波浪入射角对浮箱运动响应的影响

4 浮箱水动力响应控制及优化

4.1 减摇板-浮箱水动力模型

控制大型浮体在波浪作用下的水动力响应,提高其耐波性,对保证浮体上部设施正常使用以及工程安全具有重要意义。已有研究显示,在浮箱中部、首尾加舭龙骨可有效抑制浮箱横摇响应[19],安装减摇鳍、隔板也可减少浮箱的纵摇、垂荡等响应[20-22]。结合浮箱的形状特点,本文拟在浮箱周边安装附体装置“减摇板”以减小浮箱运动响应,并在分析减摇板布置位置及形式对浮箱运动响应影响的基础上得出较优的浮箱减摇板布设方案。

拟在纵横比2∶1的浮箱迎浪侧添加减摇板,如图5所示。由于浮箱的主要运动响应与波浪方向相关,不同迎浪面上的减摇板所抑制的运动响应类型也不同,本文以长边迎浪面设减摇板的浮箱分析减摇板对浮箱垂荡、横摇响应的控制效果,以短边迎浪面设减摇板的浮箱分析减摇板对浮箱纵摇响应的控制效果。

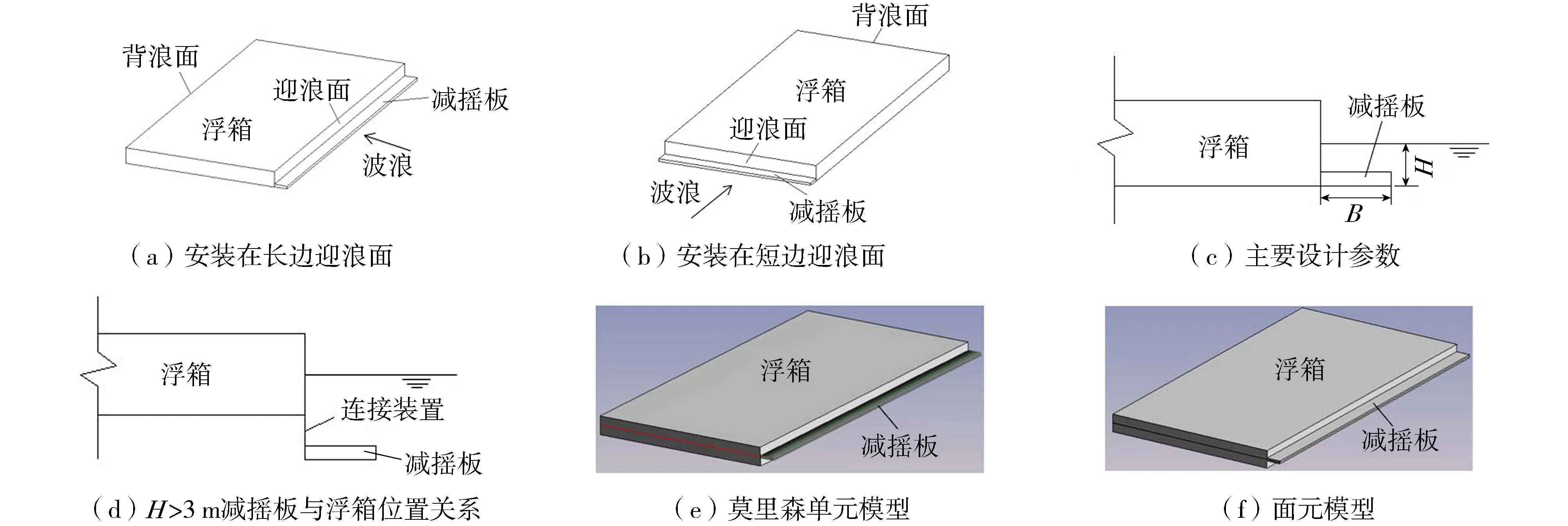
图5 带减摇板浮箱

基于简化考虑,本研究中减摇板厚度为1m,减摇板长度与浮箱迎浪面对应边长相同,主要研究参数有安装高度H(减摇板底面与水面线的距离),减摇板宽度B。当H=0.5m,水线与板中心重合,当H=3m,浮箱底面与板底面重合,当H>3m时,减摇板与浮箱相对位置如图5(d)所示,实际情况减摇板与浮箱间有桁架式连接装置连接,考虑到连接装置对浮箱运动影响较小,为简化模型,在AQWA水动力计算中不建立连接装置,视为同一个刚体,减摇板与浮箱无相对运动。

对于大尺度浮体,一般采用势流理论(式(1)～(5))计算作用在结构面上的荷载作用,当忽略流体黏性效应时,在AQWA中可采用面元模型进行计算;对于小尺度结构物,在AQWA中可采用莫里森单元建模以考虑小尺度结构上的波浪力,即采用莫里森公式(式(6))计算波浪力,考虑了黏性效应,忽略绕射作用。本文中减摇板迎浪面尺寸较小,存在阻力作用(需用莫里森单元考虑),同时又具有较大的平面尺寸,存在波浪绕射作用(需用面元考虑),故先评估2种建模方式对浮箱响应的影响。

针对减摇板安装高度H=0.5m、宽度B=5m的情况,分别采用面元和莫里森单元建模,如图5(e)(f)所示,其中,为进一步明确阻力作用的影响,莫里森单元模型设定为只有阻力作用(黏性效应),即式(6)中Cd按照JST145-2—2013《海港水文规范》取1.2,不考虑减摇板质量影响(Cm取0)。2种模型计算结果如图6所示。图6中,考虑阻力作用的莫里森单元模型峰值较无减摇板时浮体横摇响应减小0.7%,说明对于本浮箱结构,引入莫里森单元考虑减摇板黏性效应的影响较小。采用面元模型计入减摇板上绕射作用力后,横摇峰值较无减摇板浮箱减小10.8%,表明减摇板产生的绕射作用力对浮箱响应影响比迎浪面阻力更显著。此外,考虑到莫里森单元无法模拟减摇板开度,因此本文选择面元模型建模分析。

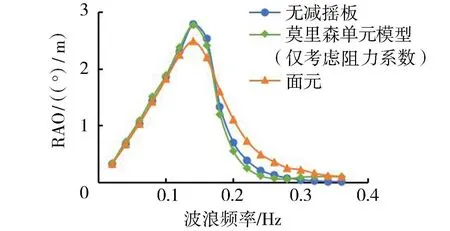
图6 减摇板建模方式对浮箱横摇响应的影响

4.2 减摇板安装高度的影响

图7为浮箱迎浪面减摇板安装宽度B=5m时减摇板安装高度H对浮箱运动响应的影响,其中,Hm为模块干弦高度(6m),原型是指浮箱未设置减摇板时的工况。计算结果显示,当减摇板安装高度H=0.50Hm时,浮箱垂荡RAO在0.1Hz处出现峰值,较原型增大了35.0%,说明减摇板与浮箱底面齐平后,增加了浮箱结构在竖直方向上获取的波浪能量,从而导致浮箱垂荡响应显著增加。当H=0.08Hm、0.50Hm时,浮箱横摇RAO峰值较原型减小了11.1%、6.5%,这是因为沿浮箱宽度方向由面元单元计入的波浪绕射荷载空间分布不均匀,并且浮箱长边减摇板水线面面积相对较大,因此安装高度影响较为显著。显然,减摇板安装高度对浮箱纵摇RAO影响不显著。

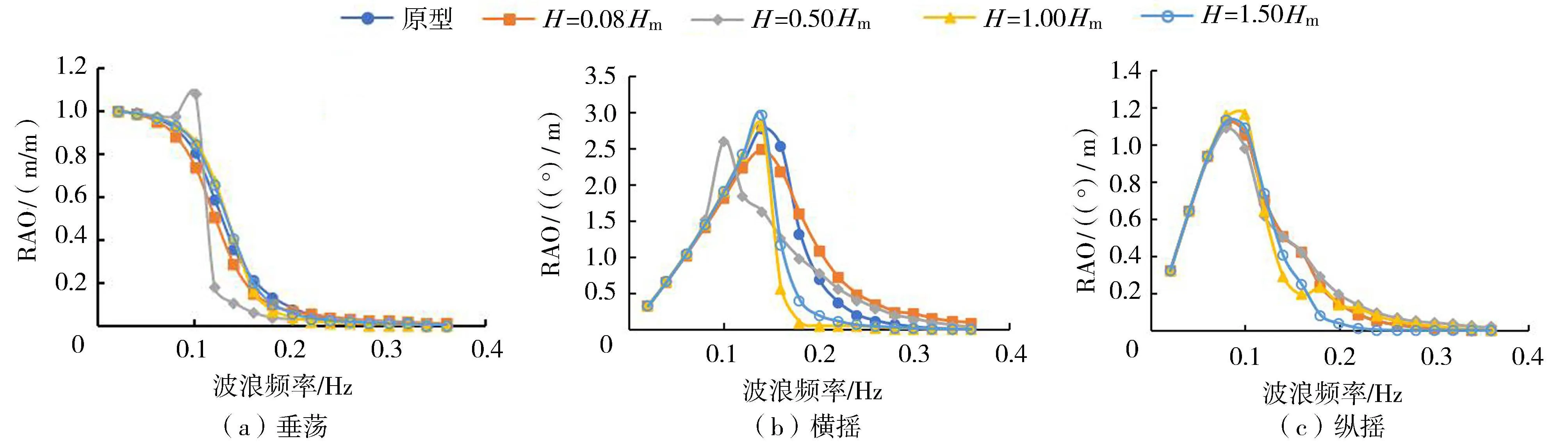
图7 减摇板安装高度对浮箱运动响应的影响

4.3 减摇板宽度的影响

图8为减摇板安装高度H=3m时减摇板宽度B对浮箱运动响应的影响,其中Bm为浮箱宽度(60m),原型是指浮箱未设置减摇板时的工况。随着减摇板宽度的增加,浮箱的垂荡、横摇和纵摇响应均有所减小,其中减摇板对横摇的控制效果较好。当B=0.25Bm时,RAO峰值较原型减小了26.5%,较B=0.08Bm时减摇板横摇控制效果提升了15.4%。减摇板对纵、横摇控制效果的差异是因为控制纵摇运动需要外界提供较大的回复力矩,因增大浮箱长边减摇板宽度对回复力矩贡献有限,如需有效控制纵摇运动,可在浮箱短边布置减摇板。

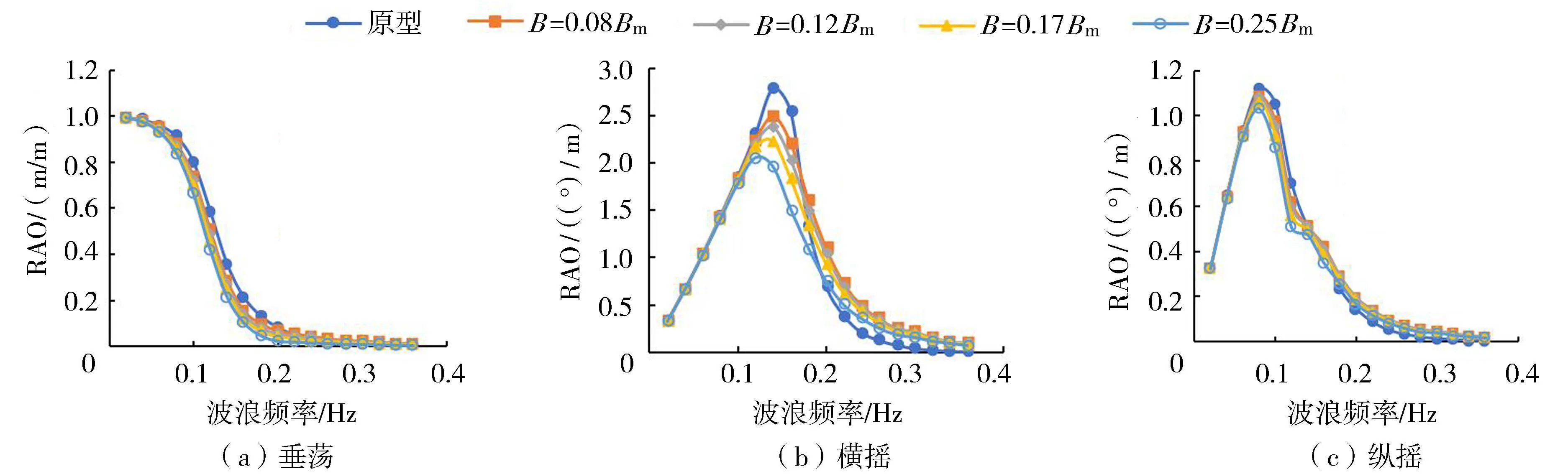
图8 减摇板宽度对浮箱运动响应的影响

4.4 减摇板形式的影响

在单侧安装单层减摇板的基础上,分析双侧安装单层减摇板、单侧安装双层开孔减摇板对浮箱减摇效果的影响。

在浮箱的迎浪面和背浪面均安装B=5m(B=0.08Bm)的减摇板,即双侧减摇板,如图9所示。图10给出了双侧减摇板不同安装高度下浮箱横摇RAO,可以看出H=0.08Hm时横摇RAO较原型减小了32.9%,比仅在迎浪面单侧有板时控制效果提高了21.8%,而其他安装高度下浮箱RAO峰值已超过原型,减摇效果较差。

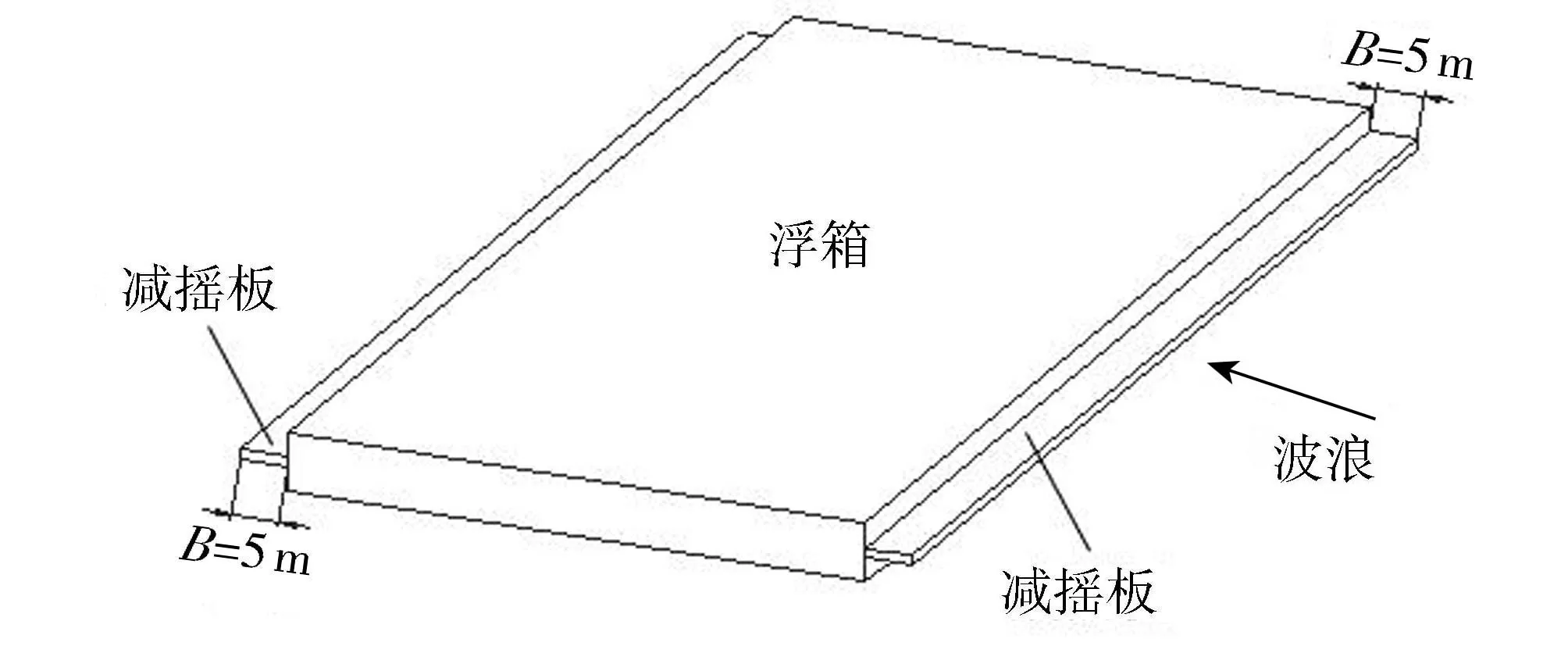
图9 双边设置减摇板

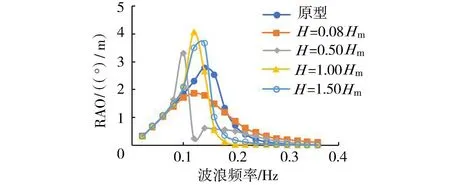
图10 双侧减摇板安装高度对浮箱横摇响应的影响

已有计算结果显示H=0.08Hm和H=0.5Hm这2种安装高度下的减摇板对横摇运动均有一定控制效果,在此基础上,设计了上板安装高度H1=0.08Hm、下板安装高度H2=0.5Hm的单侧双层减摇板布置方案,上板宽B1、下板宽B2均为5m,B=0.08Bm,并在其中一个减摇板上开孔,如图11所示,减摇板的开度ηi(上减摇板为η1,下减摇板为η2)定义见式(8)。

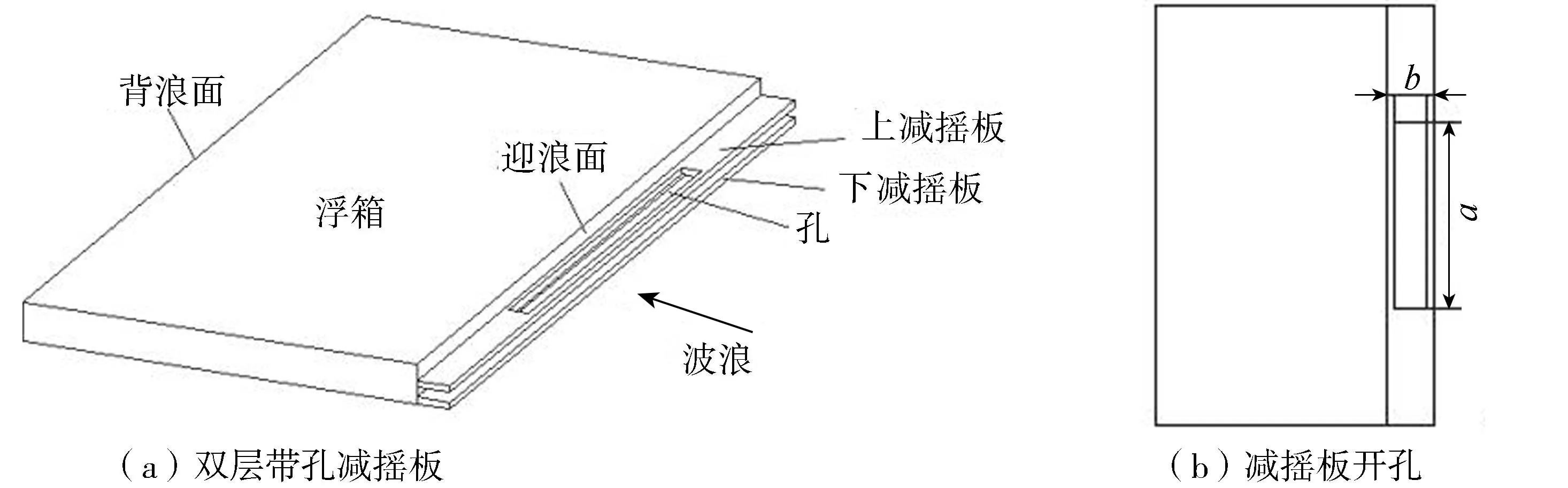
图11 双层带孔减摇板示意图

ηi=Sai/Si=ab/BL

(8)

式中:Sai为带孔减摇板中孔的面积;Si为减摇板未开孔面积;L为减摇板长度,与浮箱迎浪面边长相等。

图12为不同开度单侧双层减摇板作用下浮箱的横摇运动RAO曲线,其中上减摇板H=0.5m,下减摇板H=3m。从图12可以看出,当开度为0时,双层减摇板的RAO峰值较原型降低了12.5%。当上板开度η1增大,RAO曲线逐渐靠近只设置下层无开度减摇板时的RAO曲线;类似的变化规律同样可从下板开度η2变化中观测到。这说明双层减摇板可以近似看作上下2块单层减摇板作用效果的叠加,当双层减摇板其中之一的开度增大,该板的抑制效果也随之减小,减摇效果逐渐趋近于单层减摇板的情况。另外,对比图12(a)(b)可以发现双层减摇板时的RAO响应介于2种减摇板单独布置的情况,改变双层减摇板的开度,可以实现调整2层减摇板各自发挥比例,进而取得更优控制效果的作用。其中,下减摇板开孔的影响相对较小,当η1=40%时,双层减摇板控制效果最好。

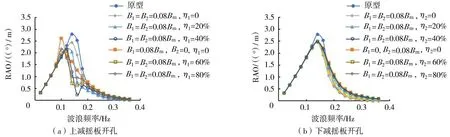
图12 双层减摇板开度对浮箱横摇响应的影响

综上,双侧单层减摇板(H=0.08Hm,B=Bm)布置方案、上板开度η1=40%的单侧双层减摇板(H1=0.08Hm、H2=0.5Hm,B1=B2=0.08Bm)布置方案的控制效果较好。基于减摇板材料用量相近考虑,进一步将上述两者与H=0.08Hm、B=2B1=0.16Bm的单侧单层减摇板横摇RAO响应进行对比,如图13所示。双侧减摇板和单侧双层减摇板的横摇RAO在计算频率范围内整体小于2倍板宽的单侧单层减摇板,其中双侧减摇板RAO峰值最小。当波浪频率大于0.14Hz时双侧减摇板布置的浮箱响应超过单侧双层减摇板的情况。基于此,本文浮箱式结构的减摇板形式优先为η1=40%的单侧双层减摇板和双侧减摇板。表1为2种形式减摇板在极限海况下对浮箱的横摇控制效果。结果显示双侧减摇板对横摇有义值的控制效果达到18.9%,η1=40%的单侧双层减摇板达到16.9%,两者差距并不显著。从工程材料经济性角度,建议优先选用上层带开度的单侧双层减摇板布置形式。

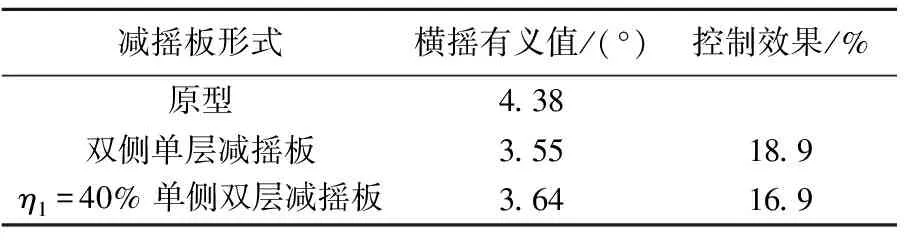
表1 极限海况下减摇板对浮箱横摇控制效果

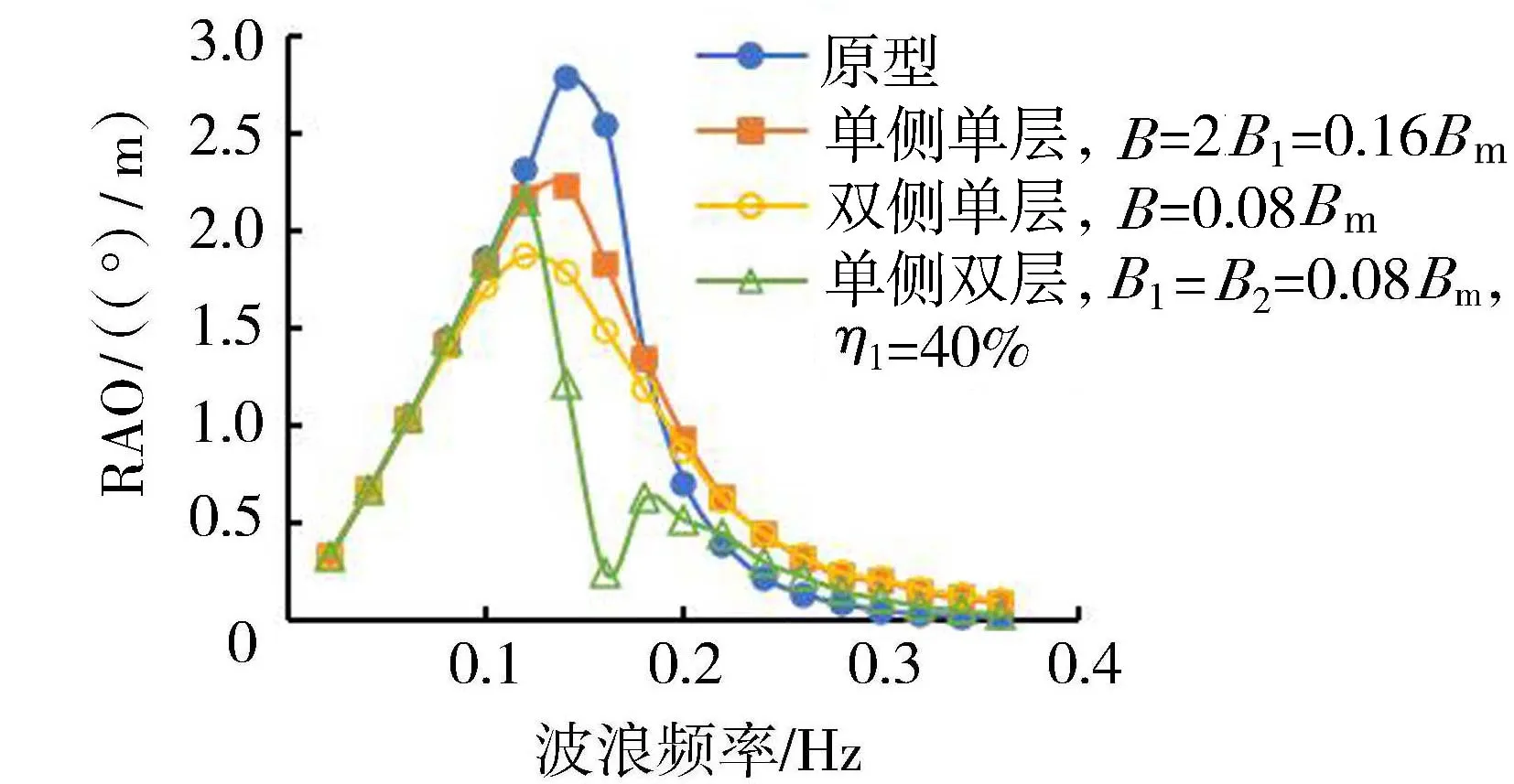
图13 减摇板形式对浮箱横摇响应的影响

5 减摇板对浮体结构强度的影响

为研究波浪作用下典型减摇板设置对浮箱结构强度的影响,建立了浮体结构有限元数值分析模型,如图14所示。其中,浮体材料采用高强度钢,浮体内部结构考虑为由纵横舱壁和纵横骨架构成的纵横板式,如图15所示。浮体的内外壳、舱壁、框架和减摇板均采用壳单元模拟,骨架采用T形截面的梁单元模拟。

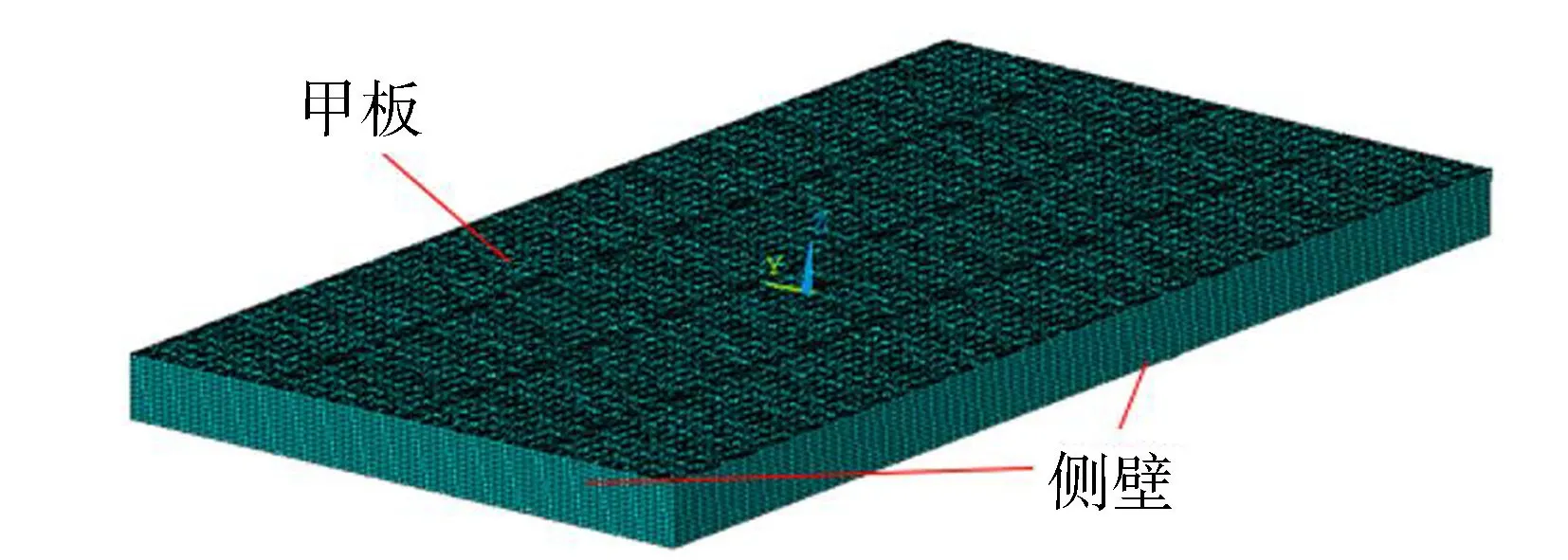
图14 浮箱结构有限元数值分析模型

图15 纵横板式浮箱内部布置

施加在浮体上的荷载包括浮体自重、压舱水重、上部(甲板)荷载、静水荷载(吃水3m)和动水荷载(波浪荷载)。考虑到实际海况的随机性和复杂性,工程中常用等效设计波方法[23]进行浮体波浪荷载的计算,采用的设计波参数见表2。

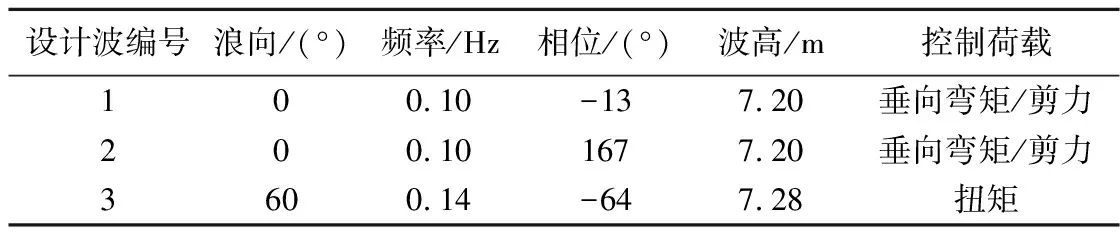
表2 设计波参数

沿浮体纵向、横向提取各设计波下外壳底板不同路径上的节点应力,如图16所示。由图17～19可以看出,在3种设计波下,有无减摇板对浮体内部结构应力影响较小,应力分布基本一致,应力峰值最大差异为23.17%。但由于减摇板的存在,原本作用在外壳侧壁的水压力作用在减摇板上,侧壁与底板或甲板相交处的应力集中有所减小,减摇板与外壳连接处出现新的应力集中位置。如图20所示,减摇板最大应力均出现在与外壳的连接位置,设计波3下的应力最大(151MPa)。除连接位置外,减摇板自身应力较小,均在允许应力范围内。综上所述,增加减摇板对浮体浮箱主体的应力影响较小,工程应用时主要应关注减摇板自身的强度及其与外壳连接处的强度。

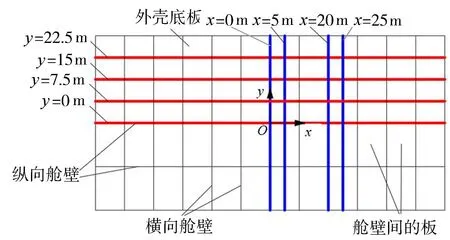
图16 外壳底板应力路径示意图

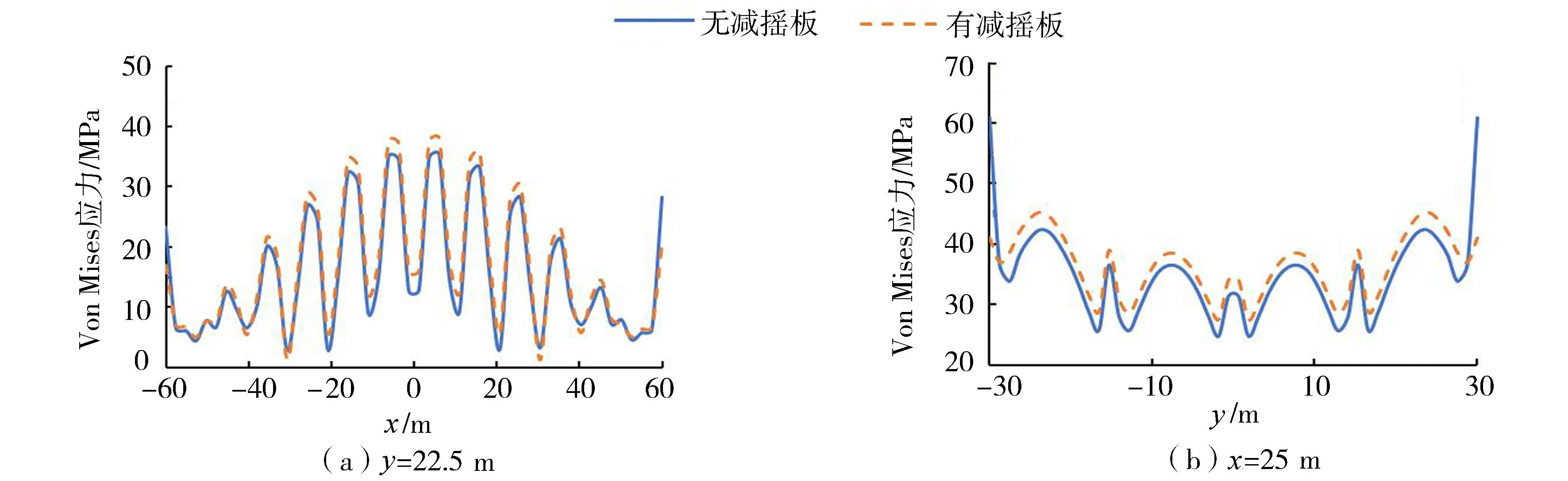
图17 设计波1下浮体有无减摇板Von Mises应力对比

图18 设计波2下浮体有无减摇板Von Mises应力对比

图19 设计波3下浮体有无减摇板Von Mises应力对比

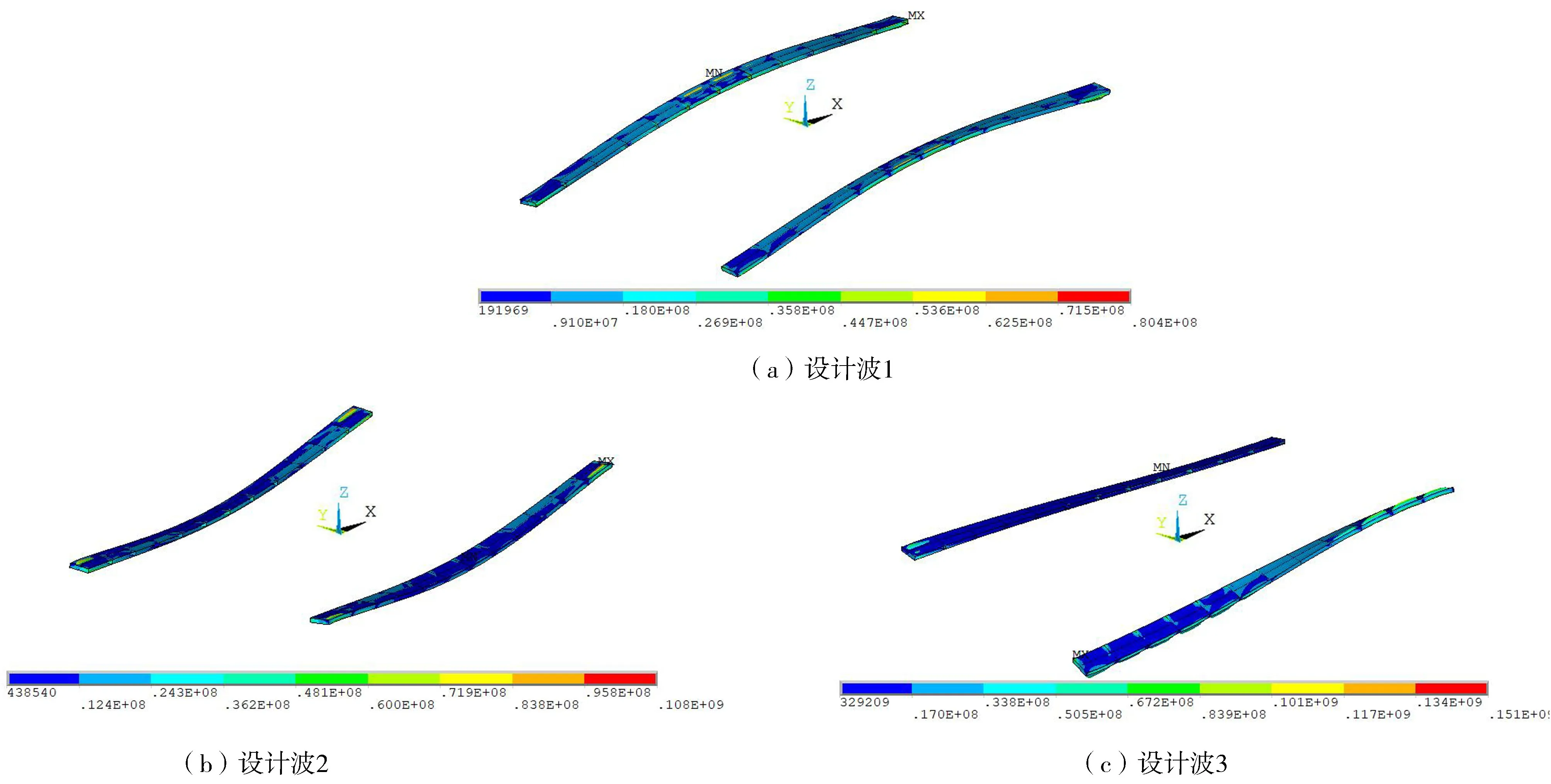
图20 不同设计波下减摇板应力云图(单位:Pa)

6 结 论

a.根据马尔代夫芭环礁海域工程水文特点,提出了大型浮体基本形式及规模尺寸,基于波浪作用下浮箱纵摇以及横摇RAO响应特性分析,明确了工程海域的优选纵横比为2∶1。不同浪向下水动力计算结果显示,横摇RAO整体较纵摇明显,在工程应用中应注意减少浮箱横摇响应;艏摇响应在45°时最显著,随波浪频率呈下降趋势。

b.浮箱侧边布置减摇板对其波浪作用下的水动力响应影响明显。浮箱吃水深度内布置减摇板有助于减少浮箱横摇响应,而减摇板沿浮箱底面齐平布置时引起的垂荡RAO响应增加了35%。随减摇板宽度的增加,浮箱的垂荡、横摇和纵摇波浪响应均有所减小,其中横摇对减摇板宽度的变化尤为敏感。

c.在迎浪面和背浪面同时安装减摇板仅在特定安装高度时产生有效的减摇抑制效果,其他安装高度下浮箱RAO峰值可能超过原型。研究提出了单侧双层减摇板开孔布置方案,计算结果表明减摇板开度影响减摇效果,其中,上层减摇板开度 40%时对浮箱横摇控制较好,极限海况下浮箱横摇有义值可降低16.9%。

d.有无减摇板对典型波浪荷载作用下浮箱结构应力的影响较小,减摇板最大应力均出现在与外壳的连接位置处,工程应用时应关注减摇板自身及其与外壳的连接强度。