一道解析几何试题的溯源及推广*

广东省惠州仲恺中学 (516229) 陈伟流

江苏省南京市栖霞中学 (210046) 苏倩倩

高考命题坚持“以核心价值为引领”,“以学科素养为导向”,“以关键能力为重点”,“以必备知识为基础”四大原则为理念,以“四翼”为考查要求解决了数学怎么考的问题,这就要求一线课堂中要充分发挥教师的主导性和学生的主动能动性,以培养学生良好的思维模式及解题习惯,促进有意义的学习;本文以2023届T8联考试题为例,浅谈对学生解题,对课堂教学提质增效的些许思考与尝试.

1 试题呈现

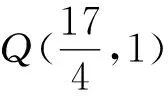
2 试题分析

2.1 内容分析

本题以抛物线为情景,有机融合了解析几何中常见的面积最值,直线过定点,斜率和(积)定值为等热门题型,知识覆盖面广,难度系数较大,渗透了数形结合,函数与方程,转化与化归,分类讨论等数学思想和数学运算,逻辑推理,数学建模,数学抽象等核心素养的考查,充分体现了高考评价体系中“以核心价值为统领”、“以学科素养为导向的”命题理念,体现三新背景下高考的新时代特点,有效呼应了高考试题的教育、评价和导向功能.

2.2 溯源分析

在试题背景的挖掘上,本题可追溯到2019人教A版选择性必修第一册习题3.3的第6题;人教B版选择性必修第一册习题2-8B第2题,03复习题第16题,第25题以及2020年山东高考第22题,归属于解析几何中“弦张直角过定点”的类型,始终围绕着曲线上的定点,弦过定点,两垂直弦这三要素为条件或结论进行有序排列命题,可进一步深度推广为更一般的手电筒模型[1],具备极大的研究价值.

3 解法分析:通法通解引领,明确运算方向

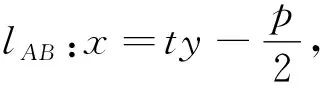
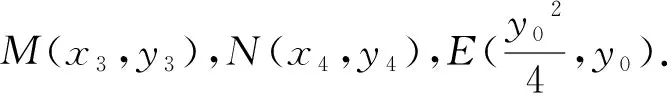
评注：以直线的横截式为切入,即有效避开了点斜式的分类讨论,又精简优化后续的运算过程.教学时教师要带领学生从不同形式的直线方程切入解题,在不同情景中领悟直线及曲线方程在消元中的利与弊,简与繁,如定点在x轴上时选择横截式可规避斜率讨论,精简运算结构;在定值,定点问题中常以斜率不存在为特殊引领,将思维历程有效化归为先猜后证的解题逻辑,让学生辩证性地认识直线方程在解题中的媒介作用,培养最值解题动机与策略,提升数学运算素养.

4 变式提升:探讨运算策略,优化解题过程

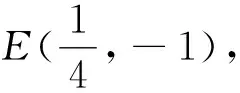
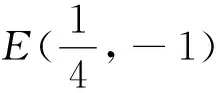
思路2：在思路1上平移建系的基础上,因点M,N是双直线lEM,lEN与抛物线的交点,又是双直线与动直线l的交点,故M,N两点具有地位上的唯一性与一致性,即两点是三曲线的共同交点,又同在抛物线上,从这两个特征出发可多角度建立关于双直线斜率的二次方程,即斜率同构法.

评注：解法1,2从曲线外部出发,通过解读两点结构特征,联立方程组抽象斜率的母方程;解法3的直线设法和定点求法分别源于人教A版选择性必修一习题2.2的第11题和习题2.3的第16题,从曲线内部出发,活用“1”的代换抽象斜率的母方程.无论从哪个角度进行同构方程,都需充分认识点M,N在题干情境的本质特征属性,才能把握同构法的逻辑根源,形成有论据、有条理、合乎逻辑的辩证解题策略,从而提升数学抽象和逻辑推理素养.

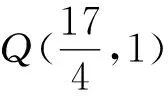
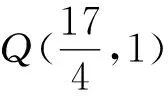
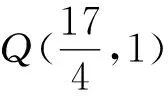
评注：重新编排曲线上的定点,直线过定点,斜率积为定值三要素的逻辑结构和相关几何条件,通法解题时学生不仅能巩固“特殊引领,先猜后证”和坐标系平移的思想方法;而且再次认识到三要素间的严密的封闭性与等价性,有助于发现问题并提出问题,形成“弦张直角过定点”的数学模型并把握模型本质,培养思维品质和理性精神,从而再次提升数学运算,逻辑推理和数学抽象的核心素养.

5 推广应用

将抛物线方程,定点E及弦张直角的性质一般化推广,有

结论1 已知E(x0,y0)是抛物线y2=2px(p>0)的定点,不过E的动直线l与抛物线交于两点M,N,若双直线lEM,lEN的倾斜角分别为α,β,斜率分别是k1,k2[2],则

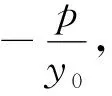
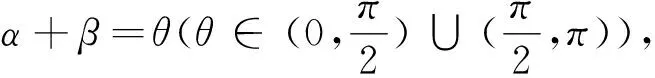
将抛物线推广到圆锥曲线体系,有

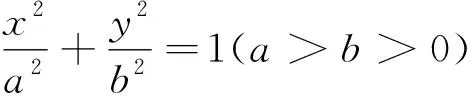
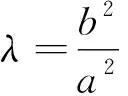
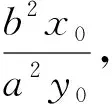
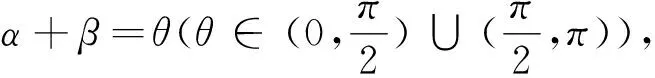
评注：对于双曲线的相关结论,只需将椭圆结论中的b2替换为-b2即可;同时对于定点E在圆锥曲线内或外,以及三种圆锥曲线进一步更统一的结论及其证明,详细见文献[3],不再赘述.