强基础 攻难点 炼思维
——高三“数值比较大小”专题教学选题及思考
江苏省扬州中学 (225009) 徐孝慧
江苏省扬州市教育科学研究院 (225007) 戚有建
一、问题提出
比较大小问题是高考单选中常见题型,考查学生分析问题,解决问题的逻辑思维.是否能透过数的大小比较确定数学知识的组织,模型的建立,已经成为近些年江苏和全国其他地区高考的一个热点.因此,作者设计和实施了以“数值比较大小”为主题的微专题课,帮助高三学生归纳总结,寻找解题方法.
二、教学选题
选题思路:笔者执教的班级学生学习基础一般,对于基本方法的掌握基本没有问题,但是不太能灵活运用,遇到复杂条件,特别是对数比较时,容易用错公式.因此本专题,从基础问题出发,引导学生从简单入手,再着重难点分析、比较,逐步加深,从而让学生跟得上、学得会、带得走.具体地,可以从一些直接或稍有变化地运用中间值或函数单调性就能解决的简单题目出发,让学生回顾、熟悉这类问题最基本的解决知识与方法,较快地进入到学习的状态;再设计几道“看不出,够得着”的典型题目,并通过边上串联,层层递进,让学生深入研究这类的函数构造方法,多角度地思考,获得多种解法.再做比较与总结,从而既掌握通法,由能学会特殊技巧,能灵活分析同类问题,恰当选择应对方式.这样,才能避免遇到此类型题时“无从下手”,避免训练时的“题海战术”,让教学有实效、更高效.
1、基础练习——强基础
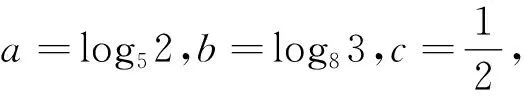
A.c C.a A.a>c>bB.b>c>a C.a>b>cD.c>a>b 练习3 已知55<84,134<85.设a=log53,b=log85,c=log138,则( ). A.a C.b 练习4 设x、y、z为正数,且2x=3y=5z,则( ). A.2x<3y<5zB.5z<2x<3y C.3y<5z<2xD.3y<2x<5z 这四道练习题都比较基础,适合大多数学生提前预习解决.在逐步提升难度的同时,关注对数性质与运算法则,尤其是换底公式,以及对数函数单调性的应用.注重基础题的问题解决的基本方法. A.a C.b A.c C.b A.a C.b A.a C.c 练习已知9m=10,a=10m-11,b=8m-9,则( ). A.a>0>bB.a>b>0 C.b>a>0 D.b>0>a 解析:随堂检测是例题的延续和变化,可以检测课堂教学效果,拓展学生的思维.这里跳出了三个数的大小比较,让学生感受问题的多样性,提升思维的灵活性.考虑到课堂时间有限,比较方法的多样性.方法一:根据指对互化以及对数函数的单调性即可知m=log910>1,再利用基本不等式,换底公式可得m>lg11,log89>m,然后由指数函数的单调性即可解出.方法二:通过观察数的结构特征,构造函数f(x)=xm-x-1(m>1),利用函数的单调性,将变量x分别取8、9、10,比出函数值的大小,得到答案.(答案为A)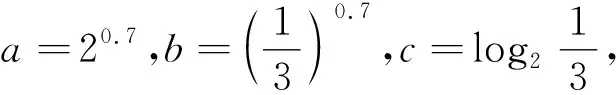
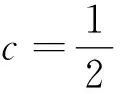
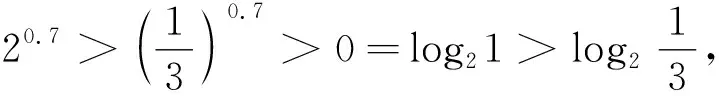

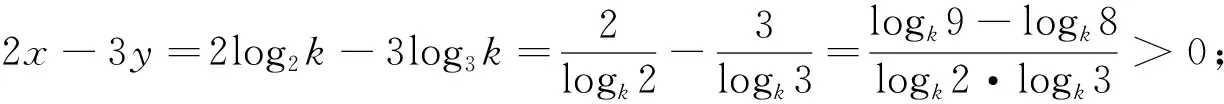
2、典型例题——攻难点
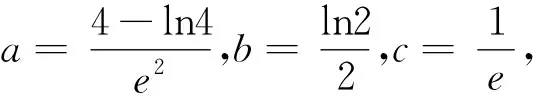
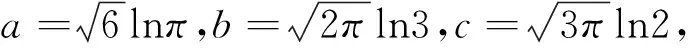
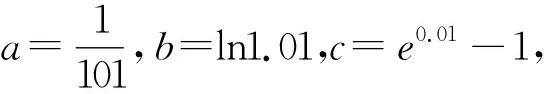
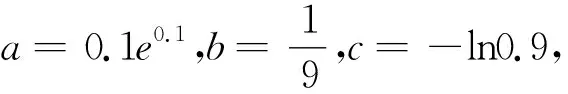


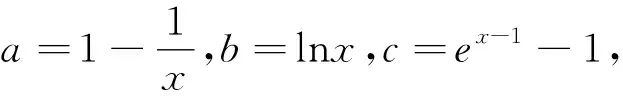
3、巩固提升——炼思维
三、教学思考