分类讨论思想在高中数学解题中的应用

李兰

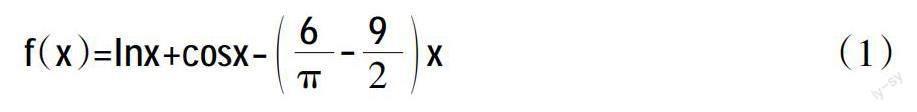
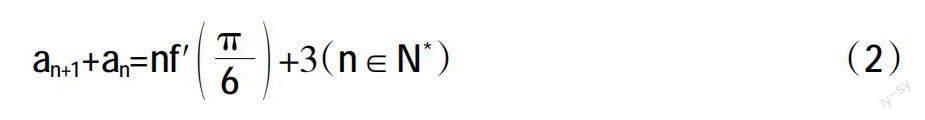
【摘  要】 通常情况下，高中数学的解题过程相当繁杂。在数学教学中，教师通过应用分类讨论思想，可以科学地发展学生的数学思维，帮助学生构建完善的数学知识体系，使学生在解答数学问题时更具有严谨性和有效性，提升学生的解题能力；可以使学生基于多个角度分析数学问题，提升学生的解题效率；可以使数学教学工作高度符合现代教育理念，保障学生的全面发展。文章论述了分类讨论思想的应用原则和应用价值，探究高中教师引导学生基于分类讨论思想解答数学问题的具体策略，旨在促使学生深入地分析数学问题、提升学生的数学素养。

【关键词】 高中数学；知识结构；分类讨论思想

一、分类讨论思想的应用原则

（一）整体完整性

在学习数学知识时，分类探究可以有效地激发学生的关联记忆能力，帮助学生掌握关键的知识结构，引导学生构建更完善的知识体系。在利用分类讨论思想解答数学问题时，一方面，学生需要完整地分析题目内容，并在拆解数学问题的过程中，重视整体和分类要素的关联性。在有效地保障了问题的完整性后，学生还需要从不同维度分析数学问题，在量化分析问题时，对问题进行模块化处理；另一方面，教师需要有效地整合各类、各项内容，促使学生的解题结果更具完整性。在解答几何问题时，教师需要对点、线、面进行分类，基于不同的侧重点展开分析，在分类讨论结束后，整合解题的过程。整体的完整性可以使学生的分类讨论过程更具实效性，确保学生能够逐步拆解数学问题。

（二）分类相斥性

学生在解答数学问题时，需要分类讨论数学题目，保证经过分类后形成的子项之间不能相互重复或相容，即划分出的各个子项要互斥、互不包含。教师在教学中，需要向学生讲述分类讨论的流程和步骤，这能够有效地激发学生的完整性记忆，极大地增强学生的逻辑思维。当分类条件相互独立时，学生需要深度解析分类后各子项的相似性，并针对多个子项进行独立论述，这能够保证学生解题过程的正确性与完整性。

（三）分类递进性

教师在数学教学中应用分类讨论思想时，需要注重层次分类，确保分类分层的递进性，使分类的各项保持独立。教师在引导学生解答应用类的问题时，需要让学生分类分析数学题目中的关键知识点，科学应用分类讨论思想，保证分类层次的递进。例如在学生解析部分平面几何的问题时，需要从多个角度分析点、线、面的关系。因此学生在参与分类讨论时，必须严格控制单一变量，并分类讨论其他两项条件。虽然该解题过程较烦琐，但是可以使不同的分类层次呈现出递进性。分类讨论问题对学生的知识体系要求较高，因此深入探讨分类层次，可以帮助学生建立完善的知识体系。

二、高中数学解题应用分类讨论思想的意义

（一）促使学生全面思考数学问题

学生在解答数学问题时，如果可以利用分类讨论思想，则可以有效地锻炼数学思维，能够从多个方向探究数学问题。学生不仅可以应用分类讨论思想、解决数学问题，还可以解决其他学科的问题，这能够使学生的想法更加深入、全面，长此以往，能够有效培养学生从个多角度分析问题的习惯。高中学生在解答数学问题时，经常会出现一些较复杂的问题，如果学生具有分类讨论的思想，则可以科学地梳理这些问题，使思路具有条理性，这能够提高学生的问题解决能力，使学生能够更全面地思考、解答数学问题。

（二）促使学生进一步理解数学知识

对于初中数学而言，高中数学的难度较高，存在很多难点知识，此时，分类讨论思想具有较高的应用优势。学生在学习数学知识时，如果可以有效结合分类讨论法，则可以深入思考相关的知识点，了解问题的根源。同时在数学学習中，数学逻辑思维对学生的进一步发展具有重要意义，可以使学生主动探究相关知识、不断优化学习方法。

（三）促使学生之间进行有效的交流与合作

高中教师在进行解题方法的教学时，需要注重锻炼学生的逻辑思维；需要引导学生自主思考，使学生在实践中能够有效的积累与学习，找出合适的学习方式。教师在组织学生基于分类讨论思想分析数学问题时，可以将学生划分成若干小组，让小组成员进行有效的合作、交流，此时，小组成员需要主动发表个人想法，由小组长梳理、总结出该小组的观点，确保学生能够在解答问题中形成共识。该方式可以大幅缩短学生的解题时间，增强学生的逻辑表达能力，使学生在与其他同学的交流中逐渐明确个人的不足，学会取长补短。

三、高中数学教学应用分类讨论思想的策略

（一）统计概率应用

对于高中数学而言，统计概率题型相对简单，教师在引导学生解答该类题型时，需要有效结合分类讨论思想培养学生的思考习惯，确保学生能够高效解决数学问题、得出最终答案。例如学生在统计集合时，部分学生可能会忽略空子集，对此教师需要重视该情况，引导学生考虑、分析空子集。

学生在解答统计问题时，需要深入研究不同的排列组合；在解答概率问题时，可能会遗漏一些要点，造成解答错误。教师需要对学生加强引导，让学生共同探究出现解答错误的原因，再利用分类讨论思想解决概率问题。这能够培养学生良好的思考习惯，使学生避免解题失误，进而保证学生准确解答数学问题，增强学生的数学素养和逻辑思维能力。例如教师在引导学生解答问题时，一方面需要深入分析该题目，让学生根据已知条件拟定各种已知问题；另一方面，学生需要基于分类思想全面探究解题对象，假设可能性的数值，最后进行分类讨论，确保获得正确答案。

（二）平面几何应用

学生在解答平面几何问题时，经常会出现动点问题，因为运动的点没有明确的方向，所以也没有明确的位置。针对此类情况，教师可以引导学生应用分类讨论思想，让学生更全面的分析问题，得出最终结果，这充分锻炼了学生的数学学习思维。一般而言，平面几何问题对学生的思考能力有较高的要求，如果学生可以有效地应用分类讨论思想，则可以保证解题思路的完整性，并能够及时地发现问题的突破口，得出最终答案。

学生在讨论平面几何的曲线问题时，需要深度解析不变项与变化项的关系，以掌握曲线类型问题的解答策略。例如，教师引导学生解答双曲线问题：已知渐近线方程y=±x，请求出离心率。在这个问题中，由于双曲线没有明确的焦点，因此无法确定离心率的数值，此时学生需要从x轴、y轴两个角度讨论离心率，解决该问题。

（三）数列问题应用

对于高中数学知识而言，数列问题是一种非常重要的题型，对学生构建数学知识网络具有重要的价值。教师在进行数列的教学时，需要让学生理解应用数学归纳法、等比数列、等差数列和基本概念等，并基于分类讨论的思想进行深入探究。在具体的教学中，教师需要引导学生自主探究应用类问题，应用分类思想深入分析具有数列分布规律的题目。在研究数列问题时，学生可以根据不同的应用场景，深度梳理等比数列、等差数列的分类过程，针对实际问题进行深入分析。在结合分类讨论思想分析数学问题时，学生可能会出现很多障碍与问题，此时教师需要深度解析不同思维模式和解题思路的建构方式，引导学生不断完善解题策略。

例如，已知函数：

式（1）的导数是f′（x），同时数列｛an｝可以满足：

需要学生回答：1.如果数列｛an｝为等差数值，a1=？2.如果，则Sn=？

在该题目中，问题1相對简单，所有学生基本都能够通过函数进行求导计算，并根据基本的已知条件进行分析解答；而问题2相对复杂，由于数列项数n的奇偶性未知，且奇偶性对an和Sn均有影响，因此教师需要引导学生进行分类讨论，探讨数列项数为奇数与偶数的情况，使学生最终得出两个不同的结论。

（四）函数知识应用

在高中数学课程中，函数是非常重要的知识点。学生在分析函数类的题目时，需要重视函数的参数变量，当参数值出现变化后，问题的答案也会形成相应的变化。教师在组织学生进行分类讨论时，首先需要引导学生进行参数分类，确保学生可以从多个层次分析问题，充分理解函数知识，使问题的分析在后期分类中具有更高的精确性。在具体应用分类讨论时，学生必须综合分析题中的已知条件与相关数据，合理地设置分类讨论层次，不能越级。教师在讲解相关问题时，需要为学生明确讲述分类的要素和具体原则，使学生对该问题有清晰的了解，避免出现遗漏。一般情况下，在高中数学中，相关定律、公式与分类讨论具有密切的联系，定理又与公式之间存在一定的限制条件，学生在推理公式、定理时，需要结合限制条件。

例如教师引导学生分析以下问题：

f（x）=4x3+ax，（x∈R）（3）

学生需要回答：1. 分析函数的单调性。2. 如果函数在中的最大值是1，则实数的取值范围是多少？

四、结语

高中数学教师在为学生讲述统计概率、平面几何、数列问题和函数知识时，需要有效地结合分类讨论的思想，引导学生从不同角度研究数学问题，帮助学生不断完善知识体系。一般而言，在解答数学问题时，学生可能会出现各种困惑，而学生通过科学的应用分类讨论思想，可以及时地解决这些困惑和问题，从而降低了学习难度，不断强化了解题能力，全面发展数学思维。数学教师在开展具体的教学工作时，需要结合现代教育理念，改进教学方式，引导学生分类讨论数学问题，使学生全面理解相关的数学知识，进而不断完善学生的知识体系，保证学生高效地掌握了数学知识、提升了学生的数学素养，推动学生的全面发展。

参考文献：

［1］ 顾培松. 分类讨论思想在高中数学解题中的应用［J］. 数理天地：高中版，2022（20）：54-55.

［2］ 曾祥均. 浅谈分类讨论思想在高中数学解题中的应用［J］. 数学学习与研究，2022（32）：146-148.

［3］ 朴希兰，朴勇杰. 分类讨论思想在高中数学解题中的应用［J］. 教育教学论坛，2015（07）：169-170.

［4］ 胡向斌. 分类讨论思想在高中数学解题中的应用［J］. 学周刊，2020（08）：85-86.

［5］ 王玉玺，曹云鹏. 分类讨论思想在高中数学解题中的应用研究［J］. 数学学习与研究，2021（15）：134-135.

［6］ 陈林. 数学思想方法在高中数学解题中的应用［J］. 数理天地（高中版），2022（21）：85-87.

［7］ 吕飞. 高中数学解题中分类讨论思想的应用［J］. 数理天地（高中版），2022（19）：84-85.

［8］ 马增杰. 浅议分类讨论思想在高中数学教学中的巧妙应用［J］. 知识文库，2022（12）：166-168.

［9］ 孙林. 高中数学解题方法与技巧探微［J］. 数理化学习（教研版），2022（04）：13-14.

［10］ 韦显杰. 在高中数学概念教学中融入数学思想方法的策略研究［J］. 天天爱科学（教育前沿），2022（02）：123-124.

［11］ 李洪涛. 高中数学解题教学中的分类讨论策略［J］. 高中数理化，2021（S1）：22.

［12］ 张菊. 渗透分类讨论思想，优化高中数学教学［J］. 文理导航（中旬），2021（11）：19.