关注发散性思维能力培养，提升初中数学课堂效率

陈月玲

摘 要：本文从初中数学的教学实践出发，指出初中数学教师要注意整合教学方式，引导学生变通认知视角，通过指导学生绘制思维导图的方式促进对知识的全方位认知，进一步优化问题设计，结合以上途径有效促进学生发散性思维能力的培养.

关键词：初中数学；发散性思维；提升策略

数学是思维的艺术，数学问题的探究过程需要研究者各项思维机能的深度介入，其中发散性思维就是一项非常重要的元素.在初中数学课堂，教师有意识地引导学生通过发散性思维来探究问题，能够帮助学生拓展认识的广度，推进认知的深度，进而让学生的探究效率得以提升，学生的思维品质也就由此获得发展.

1 整合教学方式，引领变通认知视角

当日常教学的数学课堂上，不少教师依然局限于用单一的教学手段来演绎数学知识的推理过程，这只会让原本抽象且复杂的知识变得更为乏味和枯燥.而且，单一的授课方式也将让学生的认知视角受到约束，发散性思维也会被限制［1］.因此为了让学生的发散性思维得到更大程度的训练，初中数学教师要立足学生的思维发展特点，对照课程标准研究教学内容，多角度整合教学方式，引领学生以更为开阔的视野来分析数学问题的情境，鼓励学生以不同的方法来分析同一个问题，以此来提升学生数学思维的敏感度，引领学生感悟知识之间的关系，进而自主搭建知识体系，在有效发展发散性思维的同时，也能促使课堂效率的提升.

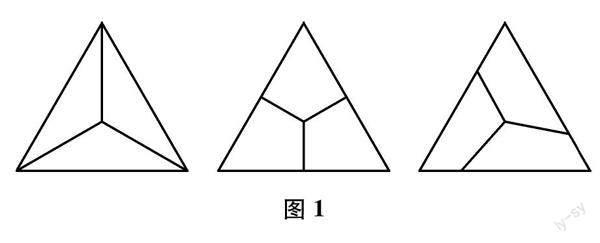
比如在几何学习过程中，学生会遇到这样的问题：现有一个正三角形，请你尝试多种不同方法，将其分割为三个全等的图形.教师可以先通过问题来引导学生组织思路：（1） 问题要求進行分割的是什么图形？（2） 正三角形有什么特点？（3） 正三角形中的角平分线、中线和各边上的高有什么特点？这些问题可以引导学生围绕正三角形将基本概念和相关特点梳理清楚，这也为学生进一步展开问题的探索奠定了基础：正三角形的三条边长度一样，且其三个内角均等于60°，中线、高、角平分线重合且相交于同一个点.从这些特点出发，教师引导学生展开讨论，鼓励学生形成探究的结论：有的学生提出，将中心和各个顶点连接线段即可得到三个全等的小正三角形；有的学生指出，可以从中心出发向三条边构建垂线，由此可以得到三个全等的四边形；还有学生提出，在第二种做法的基础上，将构建的三条线段同步同方向旋转相同的角度，以上操作如图1所示.

上述教学过程中，教师所提出的问题是一个具有发散性的问题，没有限定最终分割出图形的类型，对学生而言，他们习惯在一个确定的框架下思考问题，教师从一开始就把问题交代清楚，鼓励他们拓宽自己的思维角度，同时还引导学生通过相互讨论来进行分析和研究，这样的处理有助于学生及时分享探究的成果，也有助于学生相互启发，提升探究效率.

在引导过程中，教师要注意基础知识和基本方法依然是思维的起点，所以上述教学中，教师要让学生从全等三角形的基本特点出发，并由此展开思考.而且学生在分析和探索中也能有效展开比较，比如由第二种思路通过转动的操作得出第三种方法，这其实就是一种发散性思维的体现.问题引导、自主探究、合作研讨、总结延伸等等，正是这些教学方式的有效整合，让学生的能力发展落在了实处.

2 妙用思维导图，助力思维延伸拓展

初中数学的概念较多，概念与概念之间也存在着诸多联系，教师引导学生有效整理各个概念，能够让学生找准思维的基石，为了更好地达成这一效果，思维导图应该是非常重要的工具.思维导图是一个树状图形，整体上呈现为发散状，它往往以一个概念（或者定理、规律等等）为结点，然后向外延伸出多个知识点，这些知识又可以成为一系列子结点，并进一步拓展和延伸.思维导图不仅仅只是呈现知识之间的联系，它更能引导学生将自己的思维向外发展，让学生探明知识发展的脉络，这其实也是发散性思维的一种体现，思维导图的使用必然会促使学生的发散性思维得到发展［2］.

在初中数学课堂上，当一个单元的教学结束之际，教师可以让学生采用思维导图的方式让学生自己对各个知识进行梳理，这种整理和复习可以让学生站在更高的层次复盘知识形成的过程，这既是对学生思维的训练，也是思维能力提升的有利时机.

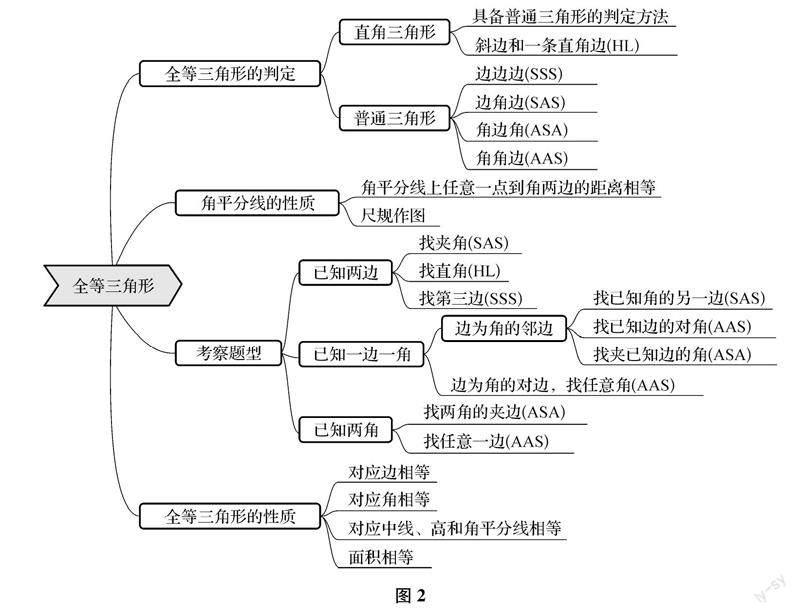
比如当学生学习过全等三角形的知识之后，教师安排任务：自主绘制全等三角形的思维导图，这个过程既能有效训练学生绘制思维导图的能力，也能帮助他们进一步强化有关全等三角形的认识.如图2所示的思维导图是教师预先准备好的一幅较为完整的思维导图，但不宜在授课之初就直接提供给学生，笔者认为应该让学生先独立自主进行绘制，鼓励学生将自己对全等三角形的认识展现在纸面上，授课过程中，笔者发现有的学生从全等三角形的基本性质着手，分析三角形的边、角、中线等关系；也有学生从全等三角形的判定出发，对判定定理进行整理；也有学生从常见的题型着手进行了整理.当学生普遍能形成自己的探究成果之后，教师可以将如图所示的思维导图展现出来，引导学生进行比较，既让学生及时完善自己的图形，同时也鼓励学生提出补充意见.笔者在学生的讨论过程中发现，不少学生都提出要将自己的理解盲点放在思维导图以示强调，笔者认为这就是一种很好的创新.

在学生采用思维导图的方式进行知识整理时，他们的思维会更加主动且活跃，一些曾经困扰他们的问题也在思考和探讨中得到了解决.因此笔者有理由认为教师要敢于在课堂上将时间给学生，让学生主动参与到思维导图的设计、描绘以及分析和总结的过程中，这对他们发散性思维的发展大有裨益.

3 优化问题设计，激活学生的数学思维

课堂提问一直是激活学生思维，引领学生探究，诊断学生学习状况的重要操作.然而，常态化的课堂提问往往功能比较单一，教师的提问过分侧重于自己的主观设计，很多问题的提出大多是为了推进教学内容的灌输，这样的问题无助于学生思维能力的发展，也限制了学生潜在能力的发掘［3］.笔者认为，教师应该基于学生的最近发展区，优化问题设计，让问题能有效推进思维向着更深层次发展，较为理想的状况是让问题成为学生的思维与知识进行对话的平台，让学生在思维中对知识形成由表及里的认知.此外，笔者也认为问题的设计要匹配不同层次学生的发展需要，让全体学生都能产生主动思考的冲动，让他们的发散性思维发挥作用.

比如在“一元一次不等式”的教学过程中，为了促使学生加强对基本概念的认识，教师可以先展示一些实例：x-12＞27、3x＜2x-1、34x＞49、-7x＞8等.联系这些实例，教师可以提出一个引导性的问题：请观察这些式子的基本特点，思考一下如何来界定一元一次不等式的概念？在问题的指引下，学生仔细观察，发现以上式子存在一个共性：均含有一个未知数，且其次数为1.在此基础上，他们能够形成一元一次不等式的概念认识，教师则进一步引导他们将思维发散开去：你能列举一些一元一次不等式的实例吗？学生在思考和举例中强化着对概念的认识.随后，教师再通过问题为学生呈现一个新的情境，让学生采用所学的知识展开研究：解不等式x-22≥7-x3.这个过程必须让学生自主探索，并让学生从中探明不等式基本性质的应用，即先将不等式转化为3（x-2）≥2（7-x），进一步整理有3x-6≥14-2x，再有5x≥20，最后得x≥4.在问题解决之后，教师提出问题：请大家总结一下一元一次不等式的基本解题步骤.

上述问题彼此之间就构建了这样一个脉络，通过多变的实例引导学生总结概念，这就是发散思维到聚合思维的转化，然后让学生自主结合概念列举实例，这是发散思维的运用，再通过问题将学生的思维集中到一个具体的问题中，这是聚合思维的体现，当问题解决之后，教师引导学生采用发散思维总结一类问题的解题步骤.这一系列过程中学生的思维得到了最大程度的训练.

在初中数学课堂上，教师整合教学方式，引导学生绘制思维导图，并通过问题引导来训练学生的发散思维，这样的教学有助于学生发散性思维的发展，且能加速学生对知识的理解.

参考文献：

［1］ 刘春桃.谈初中数学教学中学生思维能力的培养［J］.中学教学参考，2017（23）：33.

［2］ 郭金芝.育一株旁逸斜出的“智慧树”——初中数学课堂教学中培养学生发散思维的实践与思考［J］.数学教学通讯，2016（14）：3940.

［3］ 谢培培.基于发散性思维培养的数学课堂建构探索——以“同旁内角”的概念教学为例［J］.中学数学，2018（14）：89.