我国近20年数学解题研究热点与发展趋势
王泽学 陈维
摘 要:基于BICOMB2和SPSS26.0分析软件,对来自CNKI的2015篇有关数学解题的有效文献进行可视化分析,根据热点知识图谱了解我国近20年数学解题研究热点和发展趋势.我国数学解题的研究热点由“解题策略以及解题教学”;“解题反思:一题多解”;“解题思路、技巧以及思想与方法”三个方面组成.研究热点领域呈现出四大发展趋势:解题中渗透数学思想方法,培养数学核心素养;不等式问题探究;波利亚中的元认知思想;注重解题教学中反思能力.
关键词:数学解题;研究热点;发展趋势;知识图谱
2021年国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》(以下简称《“双减”政策》),指出“减轻学生过重作业负担”[1].那这是不是意味着数学习题对于数学的学习不再那么重要?曾经,在国际数学教育界就出现过“中国学习者悖论”,即中国学生的数学学习成绩优良,但其创新和思维能力不足[2].前者是我国熟能生巧理念,双基的实施等等所带来的,而后者就是过重的作业负担,机械地做题所产生的.但对于数学而言,不做题肯定是行不通的.波利亚说:“掌握数学就是意味着善于解题[3].”单壿教授在《解题研究》谈到解题重要性说;“学数学的目的,不为别的,就是为了学会解题[4].”这充分说明数学解题的重要性,那怎样解题以及解题教学在《“双减”政策》的背景下更至关重要,我国对于数学解题的研究成果也硕果累累.因此利用BICOMB2和SPSS26.0分析软件对数学解题研究领域的文献进行系统梳理,对我国近二十年数学解题研究现状以及发展趋势进行直观呈现,便于数学解题领域的研究者们进行下一步的探究.
1 研究数据和方法
1.1 研究数据
以中国知网(CNKI)中的学术期刊与学位论文作为文献来源,以“数学解题”为主题进行检索,时间跨度为2003—2022年,时间截止至2022年11月28日.检索到学术期刊论文1519篇,硕博士论文714篇,共2233篇,利用“检索—初筛—纳入—综合”4个步骤进行甄选[5],最终选定有效文献2015篇.
1.2 研究方法
利用Bicomb2和SPSS26.0软件进行分析.从高频关键词、近似值矩阵、聚类图和热点知识图谱四个方面对数学解题研究领域进行解读.这种方法不仅能直观地揭示该领域的研究热点以及热点间的关系,还能对该领域发展趋势进行预测.
2 研究过程
2.1 确定高频关键词
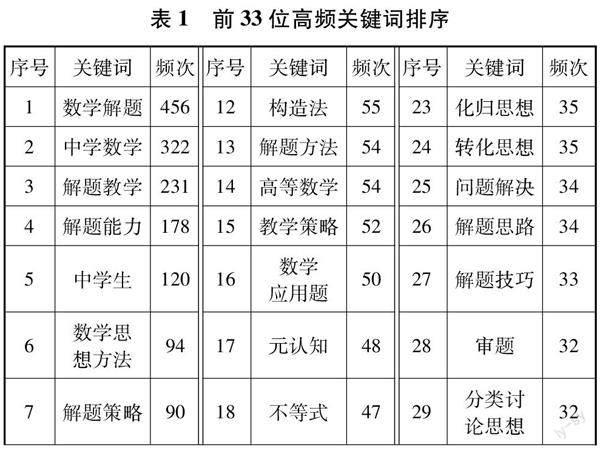
首先,利用Bicomb2分析软件提取并统计关键词,获得2538关键词;其次,将含义重合的关键词进行合并,如将“解题”和“数学解题”合并为“数学解题”等,得到有效关键词的频次为6845次;最后,截取累计频次为40%左右的关键词为高频关键词,共获得33个关键词,结果见表1.
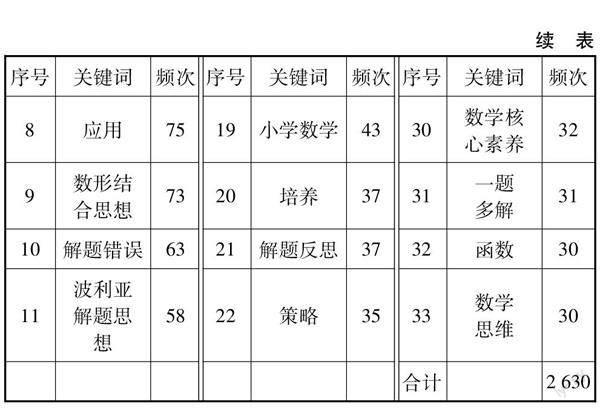
从表1可以看出,33个高频关键词的频次之和为2630次,占总频次的38.42%.其中排名前10的关键词出现频次均大于60,分别是数学解题(456),中学数学(322),解题教学(231),解题能力(178),中学生(120),数学思想方法(94),解题策略(90),应用(75),数形结合思想(73),解题错误(63).可见我国数学解题领域的研究多以中学生解题能力、解题策略、解题错误、解题中思想方法以及中学数学解题教学为主.而波利亚解题思想(58)、构造法(55)出现的频次也大于等于55,说明在解题策略和解题方法的研究中,波利亚解题思想和构造法最受关注.
2.2 生成近似值矩阵
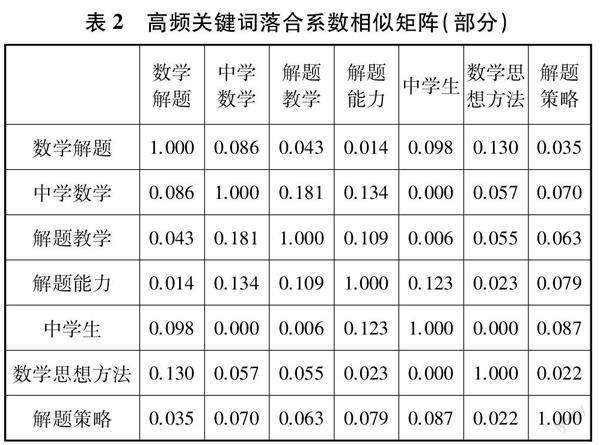
利用Bicomb2分析软件对上述的33个高频关键词进行共词分析,生成词篇矩阵并导入SPSS26.0,选取落合系数得到相似矩阵,结果见表2.
表2中的数字反映了两关键词之间的相似度,数字越大,两关键词间距离越近,相似度越高,反之距离越远,相似度越低.表2中,各个关键词到“数学解题”距离由近及远的顺序依次为:数学思想方法(0.130)、中学生(0.098)、中学数学(0.086)、解题教学(0.043)、解题策略(0.035)、解题能力(0.014).可见“数学解题”与“数学思想方法”“中学生”“中学数学”之间的距离最近,这说明研究者们在数学解题研究领域中,更关注中学阶段以及解题中的数学思想方法.
2.3 生成高频关键词聚类图
为了更直观呈现高频关键词间的关系,利用SPSS26對BICOMB2软件生成的词篇矩阵进行聚类分析,如图1所示.
图1中,纵轴数字代表与之相应的高频关键词,横轴数字代表关键词之间的距离,数字越小,表明距离越近,关系更密切[6].从数学解题高频关键词聚类图(图1)可直观看出33高频关键词被分为3大类.种类1为“解题策略以及解题教学”研究,包括解题策略、数学应用题、小学数学、解题能力、培养、审题、解题教学等16个关键词;种类2为“解题反思:一题多解”研究,包括解题反思、一题多解2个关键词;种类3为“解题思路、技巧以及思想与方法”研究,包括解题技巧、不等式、中学数学、函数、解题思路、解题方法、数学思想方法等15个关键词.
2.4 绘制数学解题研究热点的可视化图谱
用SPSS26进行多维尺度分析,并选择Z分数进行标准化,结合聚类分析结果,绘制出数学解题研究热点知识图谱.结果见图2.
从图2可以看出,解题策略以及解题教学研究(领域1)位于第三、第四象限,其中在第三象限中,“解题策略”“解题错误”“波利亚解题思想”“解题教学”“培养”“数学核心素养”“数学应用题”关键词在Y轴距离较近,这表明在解题策略中运用波利亚解题思想,数学应用题中避免解题错误以及在解题教学中培养数学核心素养研究已经形成了一定的研究规模,但并未处于整个研究网络的中心.“元认知”“问题解决”“数学思维”“审题”“小学数学”等关键词位于第四象限,是整个领域的边缘主题,研究者们很少关注,因此在培养小学数学的数学思维,问题解决中的元认知思想,数学解题中的审题等方面也需要引起重视.
解题思路、技巧以及思想与方法的研究(领域3)位于第一、第二象限,在第一象限中,“中学数学”“函数”“解题方法”“解题技巧”“解题思路”各关键词间联系较为紧密,表明中学数学对函数、不等式的解题思路、技巧以及方法研究成果较为丰富,也是现阶段此领域中的热点、重点.在第二象限中,“数学解题”“数学思想方法”等关键词联系紧密,又形成数学解题中运用数学思想方法研究领域,同时与“解题反思:一题多解”研究(领域2)位于同一象限,表明这两个领域的研究较为活跃,未来可以探究思考将这两个领域的研究与其他领域关联起来.
3 数学解题研究发展趋势分析
3.1 解题中渗透数学思想方法,培养数学核心素养
在图2中,领域3中“数学解题”“数学思想方法”等五个关键词联系较为紧密,形成在数学解题中渗透数学思想方法研究领域.经徐利治教授的倡导下,近几十年,数学思想方法已经成为广大教师频繁使用的词语,在数学解题教学中渗透数学思想方法已为广大教师所接受.因此也引来了研究者们乐此不疲地进行探究.领域1中“解题教学”“培养”“数学核心素养”三个关键词在Y轴距离较近,形成解题教学中培养数学核心素养研究领域.2014年教育部发布《关于全面深化课程改革落实立德树人根本任务的意见》,指出“研究制定学生发展核心素养体系和学业质量标准”[7].在此之后,有关核心素养的研究犹如雨后春笋般出现,而且大多数的落脚点都是如何培养学生的数学核心素养.比如在数学文化领域,也在思考数学文化如何促进数学核心素养的发展?具体有哪些途径?那不免也会将数学思想方法和核心素养之间联系起来,史宁中教授提到数学基本思想与数学“双基”“四基”、数学核心素养都是一脉相承的,基于“四基”的数学教学就是基于数学核心素养的数学教学[8].因此数学思想方法与数学核心素养有着不可割裂的联系.但从图3可以看出,“数学思想方法”“数学核心素养”这两个领域关键词的距离较远,说明其相关性不高,研究者常忽略之间的关系.所以通过“数学解题”这一桥梁,在解题中渗透数学思想方法,从而促进数学核心素养的发展是未来探究的方向.
3.2 不等式问题探究
从图2可以看出,领域3的研究热点以不等式为中心,说明数学中的解题思路,解题技巧,解题方法都能从不等式问题入手,在解不等式过程中渗透着许多数学思想方法,而且不等式在数学解题中也有广泛的应用.安振平老师提出了二十六个优美不等式[9],引来了很多读者探讨.其中李建潮利用配偶法证明第1个不等式[10];何业亮利用齐次化的解题技巧对其中第5个给出了简洁证法[11];李双娥利用极化恒等式证明其中第19个不等式[12];查正开运用数学归纳法证明第21个不等式[13];王炜利用换元法证明其中第23个不等式[14];苏建国利用函数思想证明其中第14、17、18和第19个不等式[15];卫福山通过适当的变换,利用三角不等式“变”出很多代数不等式证明其中第5、6、7和第25个不等式,这其实就是化归的思想方法[16].不等式在数学解题中的应用也比较广泛,如用基本不等式求最值,柯西不等式在几何中的应用.这足以说明不等式在数学解题中有着很高的战略价值,而优美不等式不仅仅只有这二十六个,同一不等式可以寻找新的通识解法,不等式中所展示的解题思路,解题技巧以及所渗透数学思想方法值得去深度探究.
3.3 波利亚中的元认知思想
在图2中可以看出,领域1中的“元认知”“问题解决”“数学思维”“策略”“审题”等关键词在第四象限,而这几个关键词主要围绕元认知展开.元认知是指人们对自己认知的认识[17],如解一道题过程,审题,思考解题思路,解题后反思都属于元认知.数学元认知在数学认知过程中具有重要作用,主要体现在数学问题解决、数学思维、数学学业成绩三个方面[18].而如何培养元认知能力,则可以从波利亚元认知思想着手.因为波利亚解题思想不仅是一种解题策略,也是一个完整的元认知体系.“怎样解题表”给出的“提示语”就是典型的元认知知识[19].譬如,“未知量是什么?已知数据是什么?条件是什么?”、“你知道一道与它有关的题目吗?”、“你知道一条与它有关的定理吗?”[20]等等.這些提示语都不直接拿来解题,而是在合适的时机给予正确的引导.因而在解题时经常自觉地运用这些提示语,是提高解题元认知能力的有效途径.因此,波利亚思想中含有丰富的元认知论述,是研究数学元认知的思想宝库[21].但是除了波利亚中的元认知思想,其他数学家中的数学思想是否也有着元认知思想?这值得去关注和发现.另外,在教学中,教师还能引导学生总结自己的提示语,这样学生不仅印象深刻,而且学生的元认知能力也得以提高.
3.4 注重解题教学中反思能力
波利亚在“怎样解题表”中将解题过程分为四个阶段:理解题目,拟定方案,执行方案,回顾[20].然而在教学实践中往往只注重了前三个环节,而忽视了最后的一个环节——回顾,有些甚至于把解题教学直接演变为“题海战术”[22],学生也逐渐丧失学习数学的兴趣.王华老师认为,解决数学问题有三种境界:就题论题,就题论法,就题论道[23].第一种境界就是解一道题,会一道题,每道题都是独立的存在;第二种境界就是通过这道题学会了解决问题的一般方法,能举一反三;第三种境界是解一道题,总结了一条规律,发现问题的本质.因此,教师如果只教一道题,学生就只会一道题;教师能归纳总结出问题的一般方法,学生也能触类旁通;教师如果不会反思,也教不出会反思的学生.所以教师首先要加强自身反思能力,在解题教学中提高学生的反思水平,争取做到“就题论道”[24].在图2中,领域2中“解题反思”和“一题多解”形成了“解题反思:一题多解”研究领域,一题多解就是一种很重要的解题后的反思.首先对于同一个问题,当一种解法完成后,经过回顾思考,去寻找另一种解法,一种更加简洁的方法.再进一步反思寻找不同解法之间的联系,总结共性,这也是多解归一.其次,会了一道题,更要学会触类旁通,相似的题要联系起来,寻找共同规律,归纳总结出一类题型;最后,再回到题目本身,可以通过改变条件,转换问题形式,也就是常说的变式训练,让学生更能掌握问题的本质.
4 结论与展望
对20年来有关数学解题的学术期刊论文和硕博士论文进行了系统梳理,对数学解题领域的研究热点有了更直观的了解,研究中所呈现的问题也值得关注:首先,如何让“数学解题”作为载体,使数学思想方法促进数学核心素养发展;其次,不等式在数学解题中有着非常重要的地位,从简单到复杂,每一个不等式所带来的思路、技巧以及蕴含的数学思想方法都值得去深度剖析;然后数学元认知对数学解题也有着重要的作用,除了波利亚思想中含有的丰富元认知论述以外,其他数学家思想也值得挖掘、探究,从而培养元认知能力;最后在解题过程中往往会忽略总结反思环节,教师应该从自身做起,带领学生一起进行一题多解、多解归一、多题归一的实践,从而在解题教学中提高反思能力.
参考文献:
[1] 中共中央办公厅国务院办公厅.关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见[J].中华人民共和国国务院公报,2021(22):149.
[2] 张奠基,宋乃庆.数学教育概论(第三版)[M].北京:高等教育出版社,2016.
[3] 罗增儒,罗新兵.作为数学教育任务的数学解题[J].数学教育学报,2005(1):125.
[4] 单壿.解题研究[M].上海:上海教育出版社,2016.
[5] 张楠,宋乃庆,黄新,etal.国际STEAM教师研究的热点与发展趋势——基于VOSviewer的文献计量分析[J].开放教育研究,2020,26(5):7887.
[6] 郭文斌,聂文华.我国随班就读研究热点及发展趋势[J].现代特殊教育,2021(9):1723.
[7] 《关于全面深化课程改革落实立德树人根本任务的意见》节选[J].教育科学论坛,2017(20):35.
[8] 刘祖希.访史宁中教授:谈数学基本思想、数学核心素养等问题[J].数学通报,2017,56(5):15.
[9] 安振平.二十六个优美不等式[J].中学数学教学参考:上半月高中,2010(1):136.
[10] 李建潮.配偶法证明“第一个”优美不等式[J].河北理科教学研究,2016(5):4344.
[11] 何业亮.一个优美不等式的简洁证法[J].中学数学教学,2018(1):52.
[12] 李双娥.简证第19个优美不等式[J].数学学习与研究,2017(21):142.
[13] 查正开.第二十一个优美不等式的证明与推广[J].数学教育研究,2012(4):46.
[14] 王炜.用换元法证明不等式——第23个优美不等式的别证和推广[J].数学教学通訊,2018(9):7778.
[15] 苏建国.几个优美不等式的统一证明和推广[J].数学教育研究,2012(1):6364.
[16] 卫福山.几个优美不等式的渊源及证明[J].中学数学:高中版,2012(5):7273.
[17] 袁文斌.谈元认知理论在数学解题过程中的作用[J].社会科学家,2007(S1):1545.
[18] 欧慧谋,唐剑岚.国内数学元认知的研究与思考[J].课程·教材·教法,2012,32(5):5861.
[19] 涂荣豹.数学解题学习中的元认知[J].数学教育学报,2002(4):611.
[20] G·波利亚.怎样解题[M].上海:上海科技教育出版社,2011.
[21] 徐伯华,朱凤琴.论波利亚的元认知思想[J].数学教育学报,2008(3):1416.
[22] 王宏宾,罗增儒.例谈解题回顾的意义[J].数学教学,2007(5):36.
[23] 王华.由如何获得梯形底边上的中点谈起[J].数学教学,2009(1):1819.
[24] 陈永明.数学习题教学研究[M].上海:上海教育出版社,2014.

