图记忆诱导的大气排污时序数据异常检测算法

宋文燏，周海波，吴宗培，李海员，袁玉波

（1.华东理工大学信息科学与工程学院, 上海 200237；2.河北新禾科技有限公司, 石家庄 050011）

2021 年10 月24 日，国务院印发了《中共中央国务院关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见》的文件，明确指出“大幅降低大气污染排放水平”，以“碳中和”和“碳达峰”为概念的生态环境监管治理上升至国家战略。近些年，大气污染监管治理技术备受关注。以信息化或数据化技术为基础，针对企业申报的大气排污数据，如何有效地实时在线监管大气排污数据的变化是一个技术难题。通过模型提前预测或者分析当下空气质量，可以防止造成不必要的污染排放等。

按照国家环保部的标准要求，相关企业需要每小时申报一次大气排污指标数据。从数据角度看，大气排污数据属于多维度的时间序列。随着机器学习算法的蓬勃发展，许多研究者将机器学习的方法应用于时间序列领域，根据时间序列数据的特点提出了针对性的算法，如孤立森林算法(iForest)[1]和一类支持向量机算法(one-Class SVM)[2]。随着算力的提升，深度学习算法被广泛应用，基于深度学习算法的时间序列分析方法，如循环神经网络(RNN)[3-4]和长短期记忆人工神经网络(Long Short-Term Memory，LSTM)[5-7]开始出现，基于生成对抗网络（GAN）[8]的时间序列分析方法和基于自编码器的时间序列分析方法也相继被提出。

孤立森林算法可用于无监督的时间序列异常检测[1,9-10]。一类支持向量机算法非常适合奇异值检测[2,11-13]。然而，传统时间序列检测方法只能提取浅层时序特征，效率低，并且精度也满足不了要求。随着深度学习的不断发展，许多学者将神经网络等技术用于时间序列检测异常，该技术的研究主要分为两类：一类基于预测，另一类基于重构。基于预测的模型首先对时间序列进行预测，然后通过实际值与预测值的残差来检测异常[14-17]。随着机器异常行为的不断变化，基于预测的时间序列异常检测方法的效果越来越难以提升。基于重构的模型假设在对序列数据进行重构后仅较少部分的异常数据会被丢失，如果重构后的数据与原始数据存在较大的差异，则为异常数据[8,18-21]。当前企业的排污时间序列异常检测存在以下难点和问题：（1）异常标注困难；（2）长时间序列异常检测效果不佳；（3）采用深度网络进行异常检测对性能要求高，且存在较高的时间复杂度。

本文针对上述问题采用了有标签样本与无标签样本相结合的方式，降低了标注样本所耗费的人力，同时，将时间序列进行分片，将粒度放大，然后采用图记忆网络进行特征的编码与分类，在提高检测效果的同时降低了时间复杂度。

1 图记忆诱导的大气排污异常检测

1.1 算法流程

本文提出的图记忆诱导的大气排污时序数据异常检测（IMI-TSA）算法的流程图如图1 所示。具体步骤如下：首先，将传感器采集到的数据进行预处理，并将预处理后的数据进行分窗操作；然后，结合专家判断等手段对分窗后的数据进行部分标注，有标注的样本为有标签样本，没有标注的样本为无标签样本。将有标签样本输入图记忆网络得到特征向量和类别向量，分别为图1 中蓝色部分和橙色部分，并将数据的特征向量和类别向量的向量中心进行记忆，利用该记忆预测无标签数据的类别，达到充分利用无标签和有标签样本共同训练网络的效果；最后，通过训练好的网络识别出异常的时间段。

本文算法的关键思想是通过将时间序列转化成图的方式来识别其特征，通过卷积提取有标签样本的特征向量，并与图记忆分类器得到的类别向量组合构成有一定结构的记忆，通过这种图与记忆的方式进行时间序列的异常检测。

1.2 数据采集与描述

表1 给出了某企业2018 年1 月1 日0 点到9 点申报的排污数据，具体指标有二氧化硫（SO2）、一氧化碳（CO）、二氧化氮（NO2）的平均质量浓度以及PM10与PM2.5。

表1 大气排污申报数据案例Table 1 Declaration data of atmospheric pollutant emission

将申报的排污时间序列数据记为：

其中c为企业编号；xc(i) 表示企业c第i次上报的数据，xc(i)∈Rnc；nc表示企业c所申报数据的维度，如企业c有3 个排口、5 种指标，则nc=3×5=15 ；Tc代表企业c申报时间序列的长度。

本文所用数据均为企业申报的真实排污数据，时间跨度约为2.5 a，排污数据每小时上报，总计约21 168个时间戳。在进行异常检测时，如果针对点进行异常检测，其效果并不理想，且点异常的标注工作量巨大。同时，工业生产也存在一定的周期性。所以本文将原始的时间序列数据按照工业生产的周期进行切分，将切分后的时间片序列记为，其定义如下：

其中Kc表示企业c按照工业生产周期申报的数据长度，表示第k个片段上报的排污数据，具体定义如下：

其中Tk表示第k个工业生产周期内申报时间序列的长度，如果按照每小时申报一次数据，生产周期为7 d，则Tk=7×24=168 。实际上企业有可能漏报数据，会出现Tk＜168 的情况。

1.3 时序异常数据定义

对于在环保监管部门管理范围内的企业，定义标准申报数据如下：

其中Xcnormal(t) 表示企业c在生产周期内的正常申报序列；xcnormal(i)为企业c在第i时刻正常申报数据的标准数据，xcnormal(i)∈Rnc；Tnormal为标准时间序列的长度。

其中fcnormal(i) 表示企业c在第i时刻预期内的正常申报数据，εcnormal(i) 表示企业c在第i时刻正常申报数据的准许误差范围。

定义X(t) 为异常序列，则

其中 α 是异常判定专家值，在应用过程中可由专家给定或者通过实际排查的异常序列用统计分析方法得出；‖·‖*为模型的范数。

由于实际生产线数据的情况复杂，输入序列X(t)的长度与Tnormal不相等，此时模型(6)的范数‖·‖*使用动态时间序列规整距离[22]表示，

图2 和图3 分别为点异常与上下文异常这两种异常序列的示例图。图2 所示在0～25 h 内有一个异常点，其数值高于其余点的均值。图3 所示在75～100 h 内有一个点突变，而且其上下文也发生了变化，变化后的数据有自己的变化规律，该变化规律与原来数据变化规律不同。上下文异常是本文主要检测的一种异常，企业生产规模突然发生变化或者企业排污系统出现了问题均会导致上下文异常，针对这种异常的检测可以有效防止安全事故的发生，且可以规范企业的排污行为。

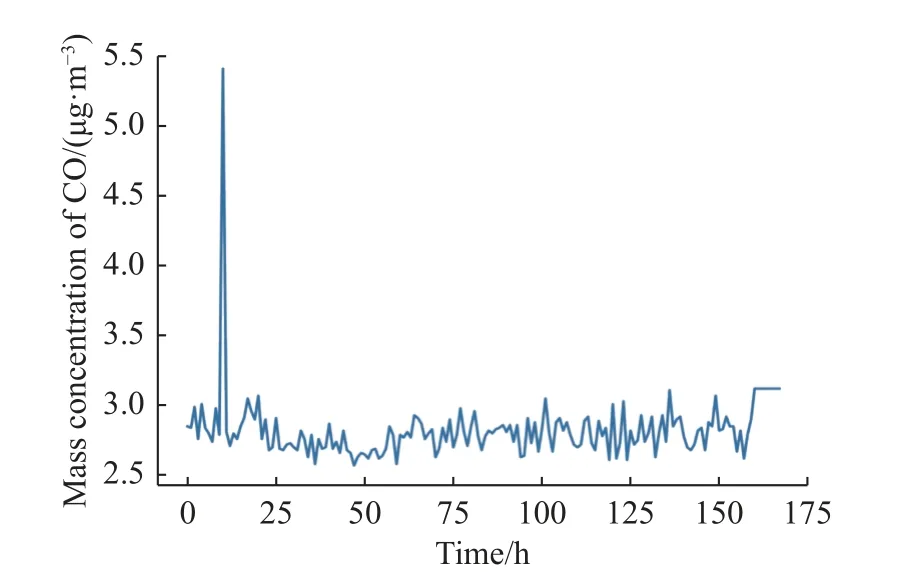
图2 点异常示例图Fig.2 Example diagram of point exception

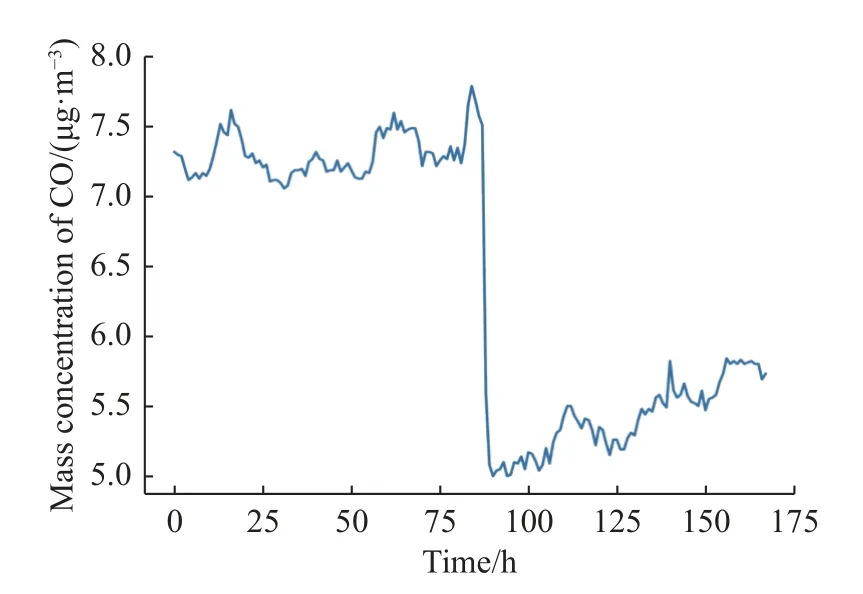
图3 上下文异常示例图Fig.3 Example diagram of context exceptions

1.4 图记忆方法

图记忆方法使用直观图像代替复杂数据序列，使得记忆变得简单和容易唤醒，常用于复杂事物的记忆领域。本文引入图记忆方法用于复杂时间序列的图记忆表达。

对于X(t) ，通过图记忆编码器对其进行编码得到与其对应的隐含空间向量，该空间向量是一个64×3的向量，将其转化成 8×8×3 的形式，并将结果映射到0～255 区间内，然后进行可视化，可以得到如图4 所示的一个色块。

图4 映射结果例图Fig.4 Example of mapping results

式(8)中G(·) 表示图记忆编码器；E∈{El,Eu}，El为有标签样本编码后对应的隐含空间向量，El={e1,l,e2,l,···,enl,l}∈Rd×nl，Eu为无标签样本编码后对应的隐含特征空间向量，Eu={e1,u,e2,u,···,enu,u}∈Rd×nu，其中d为隐含特征空间向量的维度，有标签的样本编码后得到的隐含特征空间会加入记忆模块。

通过图记忆编码器获得时间序列的特征后，再经过一个分类器，输出每个样本的类别概率分布。

其中W(·) 表示分类器模型；P∈{Pl,Pu}，Pl为有标签样本的预测类别概率，Pl={p1,l,p2,l,···,pnl,l}∈R2×nl，Pu为无标签样本的预测类别概率，Pu={p1,u,p2,u,···,pnu,u}∈R2×nu。有标签样本的预测类别会加入记忆模块与有标签样本的隐含特征空间共同构成记忆模块。记忆模块可以将从有标签样本中学习到的信息结构化进行存储，然后用来提升后续任务的性能。在记忆模块中，每次只通过有标签样本来动态地更新特征向量与类别概率向量，无标签样本对记忆模块的更新没有任何影响。记忆模块更新由两个部分组成：特征空间向量K={k0,k1} 和类别概率分布向量V={v0,v1}，ki∈Rd表示第i类的概率分布中心，vi∈R2表示第i类的类别概率分布中心，i∈{0,1} 。具体更新公式如下：

其中，η 为更新系数，1[y=i] 表示指示函数，ni为类别i中样本的数量，ej,l表示有标签样本中第j个样本编码后的隐含空间向量，pj,l表示有标签样本中第j个样本的类别概率。在不引入任何先验知识的情况下，将K中的元素都初始化为0，将V中的元素都初始化为0.5。

1.5 图记忆诱导的大气排污异常检测模型

通过有标签样本学习到的知识，可以进一步获得无标签样本预测的类别概率向量，且通过该概率向量可决定最后的样本类别。

其中w(ki|x) 表示根据样本的特征向量e到每个类别中心ki的距离得到的权重；dist(·) 表示距离函数，本文采用的是余弦距离。

1.6 模型目标函数

本文将训练模型阶段分为有监督学习和无监督学习，有监督学习采用信息熵损失：

无监督学习采用信息熵与KL 散度结合的方式：

因此，无监督学习损失为：

其中 µ1和 µ2表示信息熵与KL 散度之间的权衡系数。

模型的损失函数为有监督与无监督损失之和：

其中 α 和 β 分别表示训练样本中对有标签与无标签数据的重视程度。在没有任何先验知识的情况下，本文初始化 α ，β 均为0.5。在模型训练过程中需要加入记忆模块；在测试阶段只需要用训练好的模型来获取最后的类别概率向量，不再需要加入记忆模块，从而减少了存储和额外的计算消耗。

2 算法设计与分析

2.1 算法流程

图记忆诱导的大气排污时序数据异常检测算法描述如下：

输入：有标签样本Xl，有标签样本标签Yl，无标签样本Xu，批处理数（batchsize ），迭代次数（epoch ）

输出：异常类别特征

其中 MemoryNet(·) 表示图记忆网络，通过图记忆网络可以得到特征向量el和类别向量pl，然后更新记忆模块的特征中心向量ki和类别中心向量vi，i表示所属类别。通过有标签的样本得到记忆后，利用得到的记忆来预测无标签样本的类别，通过图记忆网络可以得到无标签样本的特征向量eu和类别向量pu，然后计算出eu到ki的距离di，通过di计算出各个类别的权重系数wi，wi与vi相乘并求和，最后得到通过记忆预测的类别向量pu，将pu作为无标签样本的类别概率。

2.2 复杂度分析

IMI-TSA 算法主要由图记忆编码器、分类器和记忆模块组成。图记忆编码器输入的是一段序列，由卷积神经网络捕获序列时间与空间上的特征，然后通过分类器将获取到的特征映射到类别概率空间中，最后通过记忆模块将从有标签样本中学习到的知识存储起来。为了提高分类速度，本文采用的模型是浅层网络，具体而言，图记忆编码器包括1 个全连接模块，2 个卷积模块，其中卷积子模块中包含1 个二维卷积层、1 个池化层和1 个激活函数，分类器则是由3 个全连接模块构成，其中每个全连接子模块中分别包含1 个线性层、1 个dropout 层和1 个激活函数。

IMI-TSA 的时间复杂度为O(n) ，其中n为输入样本的数量级。

3 实验结果及分析

3.1 数据集

本文从水泥、炼焦、钢铁和玻璃制造4 个行业中各选取2 个企业为代表，针对这8 个企业的大气排放浓度均值指标进行实验，该指标的数据总共有21 168个时间戳，每个时间戳以小时为单位。

首先对数据进行预处理，包括负值修正和填充缺失；然后通过一个异常标注器对预处理后的数据进行异常点标注；最后将标注后的数据进行分窗处理，窗口大小设置为7 d，即168 个时间戳，滑动窗口的步长设置为84，通过分窗后得到250 个样本作为实验数据。由于滑动窗口的设置会影响样本数量以及最终模型的效果，滑动窗口步长越小，分窗后得到的样本数量越多，结合本文所针对的实际问题以及最终效果综合考虑，选择了效果较优的步长。对分窗后的时间序列进行标注，如果该窗口的时间序列标注中包含一个或多个异常点时，则这段时间序列被标注为异常。

数据标注完成后，将其中175 个样本作为训练集数据，75 个样本作为测试集数据。为了还原工业背景，实际有标注的数据极少，故在训练集中只有70 个样本带有标签，剩余105 个样本无标签。表2给出了训练集和测试集的异常样本数量以及测试集和训练集总的样本数量。

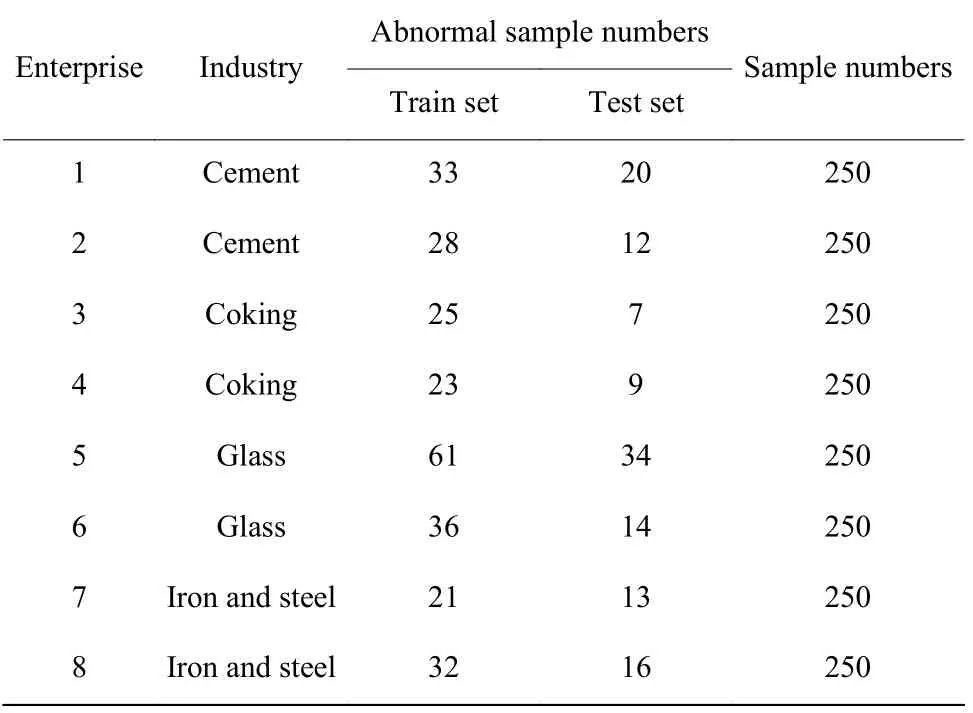
表2 异常样本分布Table 2 Distribution of abnormal samples

3.2 对比方法与实验设置

为了检验IMI-TSA 算法的可行性与优越性，选取了以下4 个方法进行对比。

（1）K 近邻（KNN）：KNN 算法取每个样本周围大小为3 邻域的样本点。

（2）支持向量机（SVM）：SVM 算法采用的惩罚参数设置为1，核函数为径向基函数，设置值为20，其他参数为Sklearn 包的默认值。

（3）浅层的全卷积网络（FCN）：FCN 算法采用3 层卷积神经网络结构，每层网络内部结构跟本文方法卷积子层的内部结构相同。IMI-TSA 算法以及FCN 算法的训练模型设置为32，优化器采用随机梯度下降进行参数优化，学习率大小初始值0.1，学习率采用步长衰减的方式进行更新，衰减率为0.95，衰减步长为10。

（4）TADGAN（Time-series Anomaly Detection using Generative Adversarial Networks）：TADGAN 算法停用了70%的数据，即14 818 个时间戳，在剔除异常样本点后用于模型的训练，其中训练模型的epoch设置为40，batch size 设置为168。TADGAN 算法训练完成后，用训练好的模型对训练集和测试集的样本进行异常检测，如检测有异常则标注为1，检测没有异常则标注为0。

3.3 评价指标

采用准确率(A)、精确率(P)、召回率(R)和f1值作为算法检测性能的评价指标。

其中T1表示预测为异常且实际结果也异常的样本数量，T2表示预测为正常且实际结果也正常的样本数量，F1表示预测结果为异常但实际为正常的样本数量，F2表示预测为正常但实际结果为异常的样本数量。

3.4 实验结果

不同算法对水泥行业中企业1、2 数据集的分类效果如表3 所示。对于企业1，IMI-TSA、KNN 和FCN算法在训练集上的分类效果较优，在保持较高的准确率和精确率的条件下拥有较高的召回率和f1 值，其中IMI-TSA 算法极大地提高了召回率和f1 值。TADGAN 算法的召回率最高，但是其精确率较低，说明该算法找出异常比较全，但对异常过于敏感。虽然IMI-TSA 算法的召回率比TADGAN 算法低了0.13，但是IMI-TSA 算法的整体效果较优。在测试集上，IMI-TSA 算法的f1 值超过0.60，能够比其他模型更好地学习到时间序列的特征并有更佳的分类效果。

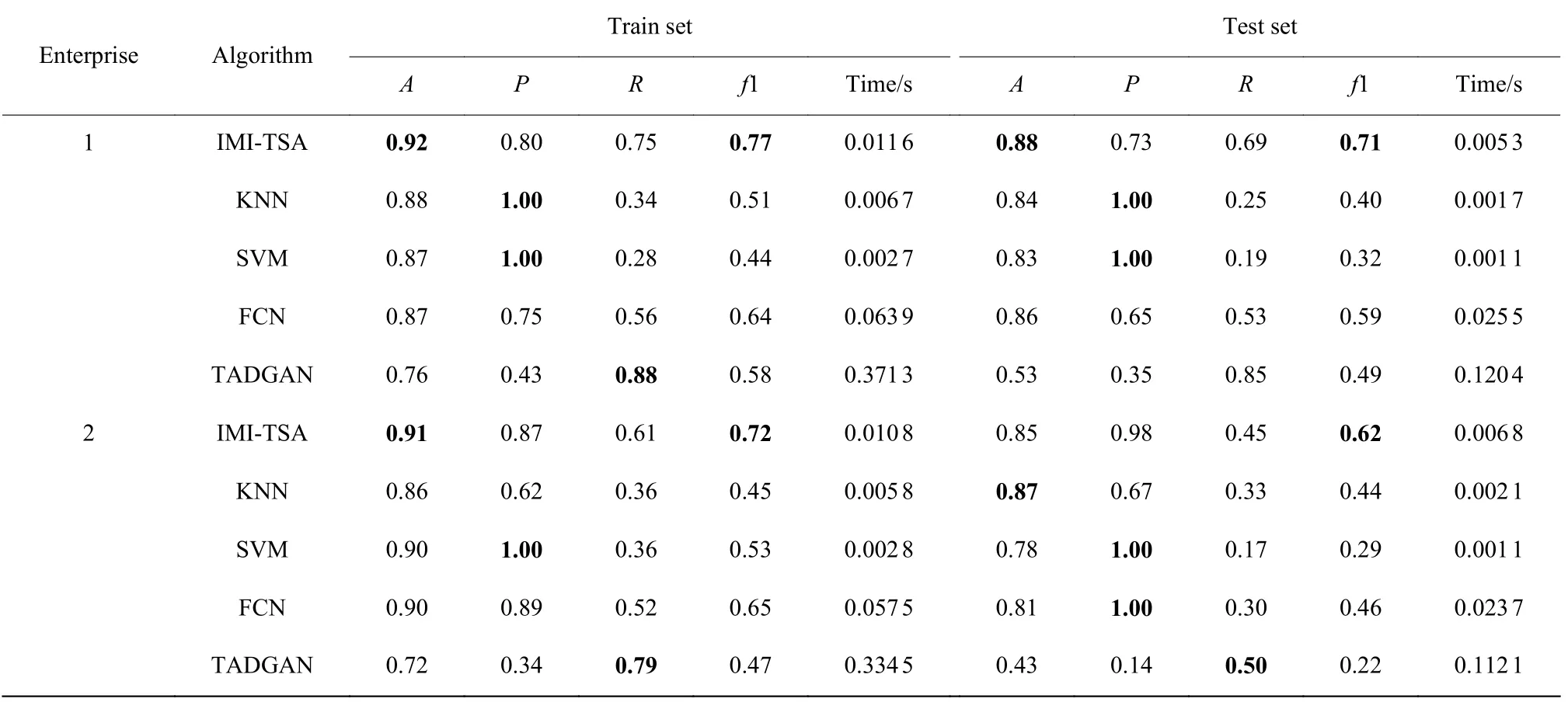
表3 不同算法对水泥行业数据集的分类效果Table 3 Classification of different algorithms on data set in cement industry

在时间复杂度上，不管是训练集还是测试集，TADGAN 算法最耗时，KNN 算法和SVM 算法耗时较少，IMI-TSA 算法虽然比KNN 算法和SVM 算法耗时要多一些，但是比它们拥有更优的分类效果。FCN 算法有较好的分类效果，但是IMI-TSA算法比其节省了更多时间，并且在分类效果上也比FCN 算法有所提升。

对于水泥行业中企业2，在训练集和测试集上，IMI-TSA 算法和FCN 算法的分类效果较优，在保持较高的准确率和精确率的条件下拥有较高的召回率和f1 值，IMI-TSA 算法相比FCN 算法，有更高召回率和f1 值，耗时也更少。

从水泥行业这两个企业的结果来看，IMI-TSA算法在f1 值上能够保持较好的水平，虽然耗时上相比于机器学习算法略有差距，但是相较于同等级的深度学习算法FCN 算法和TADGAN 算法，在时间上的优势还是较为明显的。

不同算法对炼焦行业中企业3、4 数据集的分类效果如表4 所示。对于企业3，IMI-TSA 算法的召回率和f1 值明显高于其他算法，TADGAN 算法虽然有较高的召回率，但是其准确率、精确率和f1 值都较低，把较多的正常样本分类为异常，而其他的算法在测试集上的召回率和f1 值由于数据的不平衡导致其效果非常不好。FCN、SVM和KNN 算法都能比较精准地找出异常但是找得并不完全，所以数据不均衡较为严重时，其效果会降低，f1 值最高只能达到0.50 左右，如SVM 算法在该行业中的精确率和召回率出现了0 的现象，说明该算法没有找出异常样本。IMI-TSA 算法在数据不均衡的情况下，能有比较好的效果，保持较高准确率、精确率以及召回率，同时f1 值也最佳。虽然IMI-TSA 算法在时间消耗上相较于KNN 和SVM 算法略有差距，但其差距仍在可接受范围内。

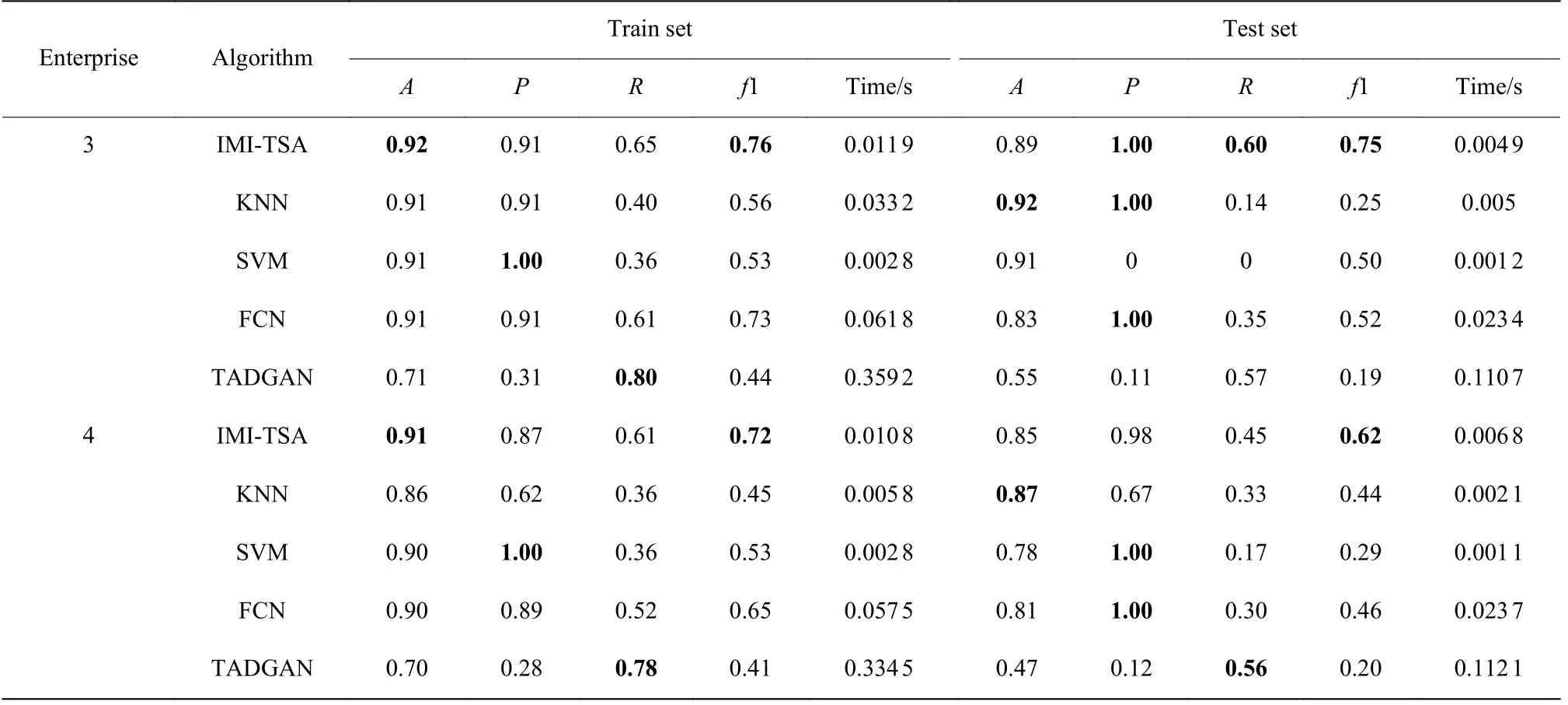
表4 不同算法对炼焦行业数据集的分类效果Table 4 Classification of different algorithms on data set in coking industry

企业4 的异常样本数量较企业3 稍多些，SVM算法的精确率和召回率并没有出现0 的现象，由此可以说明SVM 算法在数据样本不均衡较严重的情况下的稳定性不好；由测试集上的召回率和f1 值可以看出，IMI-TSA 算法更优。相较于SVM、KNN 算法，FCN 算法在处理不平衡数据时性能相对稳定，但是时间消耗略高。TADGAN 算法在异常样本数较少的情况下，召回率和精确率都有所下降，导致f1 值较低。

炼焦行业中的数据样本不均衡情况最为严重，FCN 算法在训练集上的效果较好；TADGAN 算法对异常过于敏感，在异常样本数量下降后，其效果也随之降低，f1 值在测定集上只能保持在0.20 左右；而IMI-TSA 算法召回率和f1 值均比训练集低，但是能保持比较稳定的水平。

不同算法对玻璃制造企业5、6 数据集的分类效果如表5 所示。企业5 的异常样本数据最多，异常数据占了30%～40%。

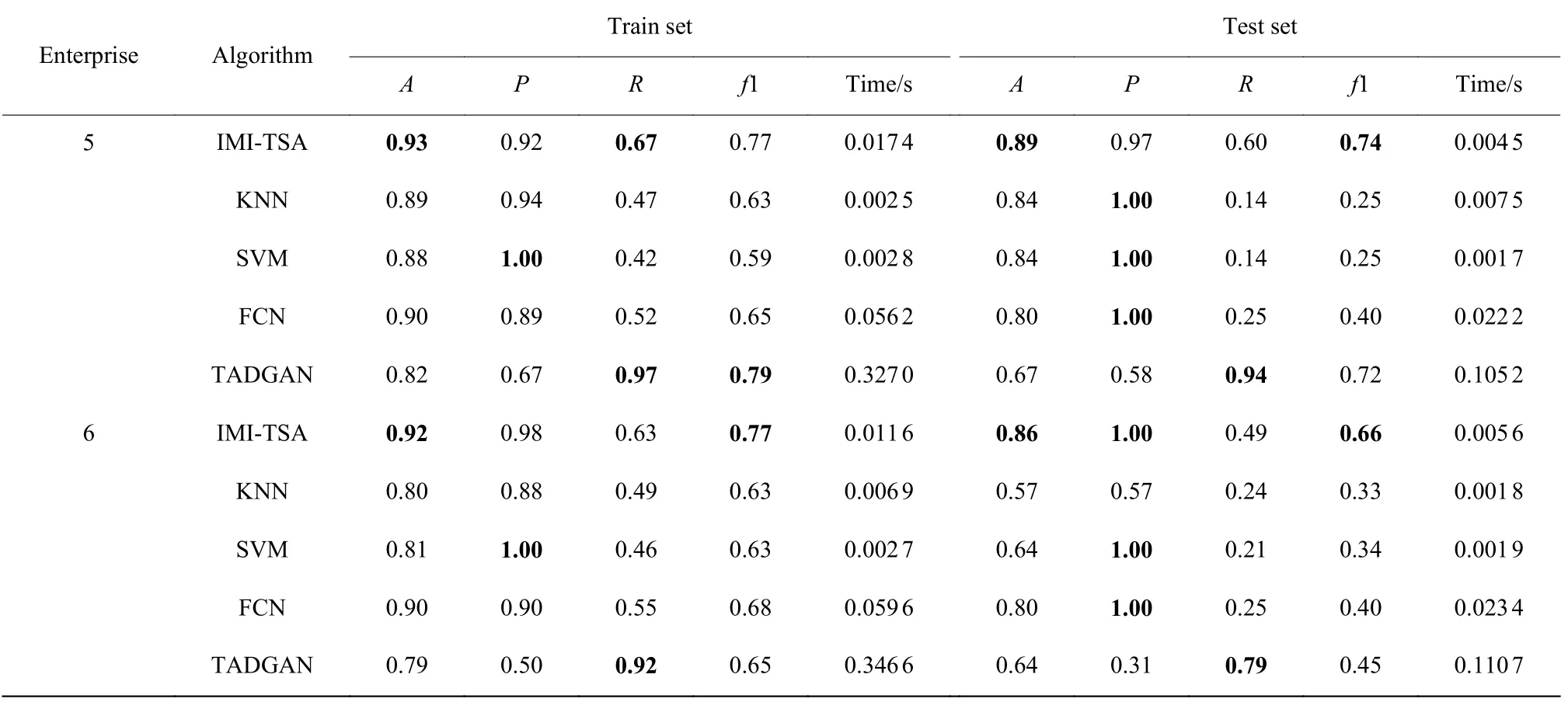
表5 不同算法对玻璃行业数据集的分类效果Table 5 Classification of different algorithms on data set in glass industry

与企业1～4 相比，SVM 算法在企业5 的训练集上的召回率和f1 值均有提升，IMI-TSA算法的召回率和f1 值在测试集和训练集上都能保持在0.60～0.70，说明在异常数据量较多的情况下，IMI-TSA 算法在测试集上能比较好地学习到数据的特征。TADGAN 算法在异常样本数较多的情况下，在训练集和测试集上的召回率均超过了0.90，且f1 值也较高。对于企业6，IMI-TSA 算法在召回率和f1 值上较优，其异常样本数量较企业5 有所减少，但在测试集上的效果有所下降。

在玻璃制造业中，企业5、6 的异常样本数量较多，IMI-TSA 算法在训练集上的f1 值还能保持在0.60～0.70，TADGAN 算法在训练集和测试集上的效果较异常样本数量较少时有所提升。由此可见，在样本较为平衡的情况下，IMI-TSA 算法性能较佳，且在数据分布不平衡的情况下，也能够保持较为稳定的效果。

不同算法对钢铁行业中企业7、8 数据集的分类效果如表6 所示。对于企业7，IMI-TSA 算法的召回率和f1 值在训练集上分别保持在0.60 和0.70 左右；在测试集上，召回率和f1 值分别为0.50 和0.70 左右。相较于KNN 和SVM 算法，IMI-TSA 算法在训练集和测试集上的效果都明显更佳。TADGAN 算法虽有较高的召回率，但其总体效果不佳，且时间消耗较高。

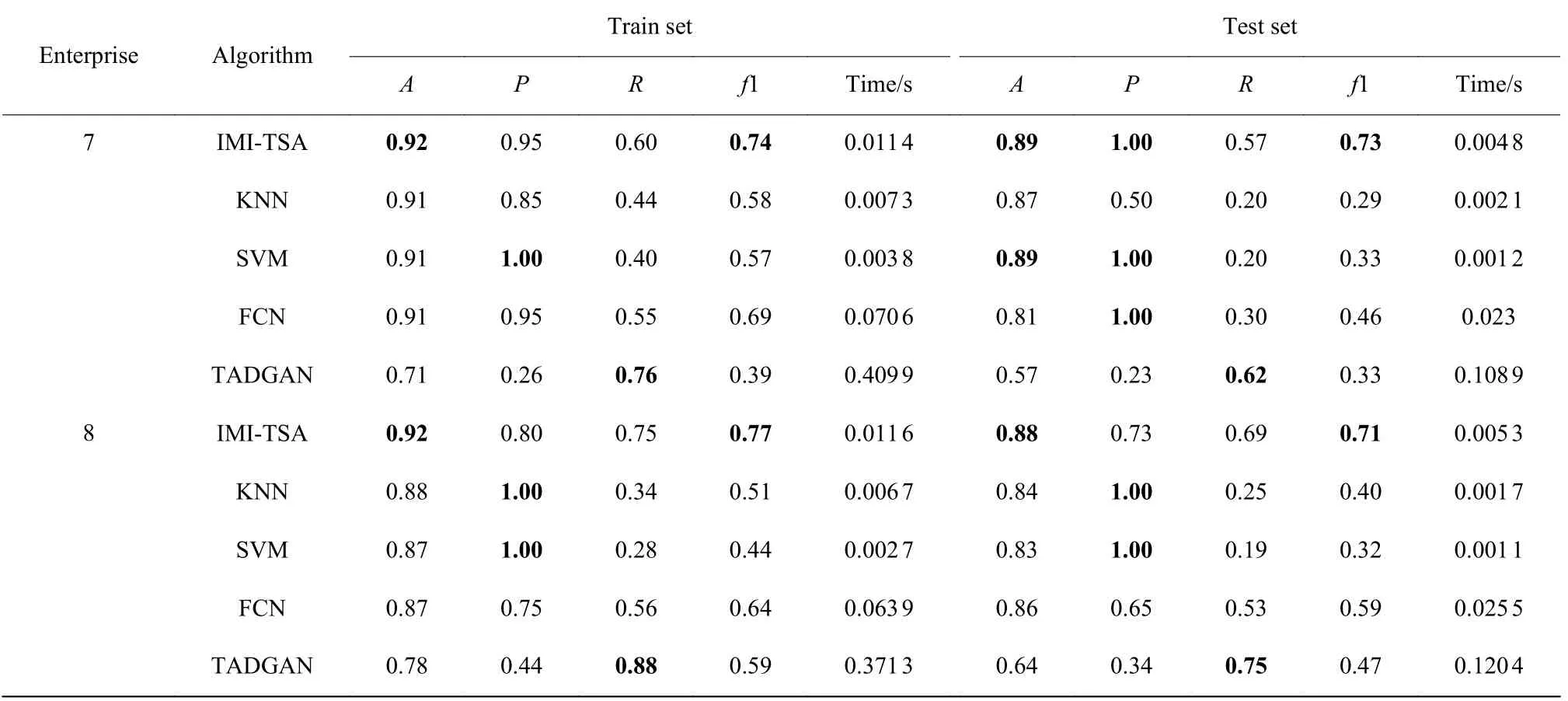
表6 不同算法对钢铁行业数据集的分类效果Table 6 Classification of different algorithms on data set in iron and steel industry

对于企业8，IMI-TSA 算法在训练集上的召回率和f1 值分别为0.75 与0.77，其在测试集上的召回率和f1 值分别为0.69 与0.71，较企业7 的效果有所提升，且企业8 的数据平衡性比企业7 高，所以在测试集上的召回率和f1 值都有所提升。

结合钢铁行业两个企业的结果来看，TADGAN算法都能保持较高的召回率，但其对于异常过于敏感，在异常样本量较少情况下，整体效果不佳。KNN和SVM 算法能够有较高的准确率和精确率，但是其召回率较低，整体效果略低，FCN 和IMI-TSA 算法的准确率与SVM、KNN 算法相近，但精确率有所下降，召回率有所提升，整体效果高于SVM、KNN 算法，而IMI-TSA 算法的整体效果比FCN 算法略高，且时间消耗也更少。

综合以上不同算法对8 个企业数据集的整体效果，TADGAN 算法对于异常过于敏感，在异常样本数量较多的情况下效果提升明显，但是当异常样本数较少时，总体效果不佳。SVM 和KNN 算法对于异常并不敏感，在异常样本数量较少时，其召回率较低，FCN 与IMI-TSA 算法的效果较为稳定，但IMI-TSA算法的整体效果优于FCN 算法。时间消耗上，TADGAN算法的时间消耗最高，SVM 和KNN 算法的时间消耗最低，IMI-TSA 与FCN 算法时间消耗处于两者之间，IMI-TSA 算法比FCN 算法更节省时间。

4 结束语

IMI-TSA 算法用有标签样本建立有结构的记忆，然后利用样本间的特征与类别的关联性通过记忆来获得无标签样本的类别，并通过有标签样本与无标签样本结合共同完成时间序列异常检测任务。

采用IMI-TSA 算法在8 个企业的生态环保数据集上进行实验，准确率都达到了80%以上，并且在测试集上f1 值达到了60%以上。相较于其他算法，IMI-TSA 算法在不均衡数据上也能较为稳定地捕获数据特征，并且具有较好的效果，但仍然存在局限性。IMI-TSA 算法在时间段上进行异常检测时，粒度不够精细，所以在接下来的研究中，将结合粒度更加细的模型共同完成异常检测的任务。