基于并行LSTM-CNN 的化工过程故障检测

肖飞扬，顾幸生

（华东理工大学能源化工过程智能制造教育部重点实验室, 上海 200237）

随着智能化和自动化的不断发展，化工过程的投资和生产规模越来越大，化工生产装置也向着越来越复杂化和大型化的方向发展。化工生产过程中的异常工况应被及时检测和诊断，如不及时发现并处理，会造成财产损失和环境污染，甚至威胁人的生命安全。因此，研究故障检测和诊断(Fault Detection and Diagnosis，FDD)方法，及时有效地检测故障的发生，对于保障企业生产安全和人身安全具有重要意义[1]。

FDD 方法一般分为3 类：基于专家经验的方法、基于模型的方法和基于数据驱动的方法。数据驱动的FDD 方法可以进一步分为多元统计学的方法、浅层学习方法和深度学习方法。多元统计学包括主成分分析(Principal Component Analysis, PCA)[2]、偏最小二乘(Partial Least Squares, PLS)[3]、独立主元分析(Independent Principal Component Analysis,ICA)[4]和Fisher 判别分析(Fisher Discriminant Analysis,FDA)[5]等，这些方法被广泛应用在线性特征判别的问题中，但对工业过程的故障检测效果不够理想。浅层学习方法包括：人工神经网络(Artificial Neural Networks, ANN)[6]、支持向量机 (Support Vector Machines, SVM)[7]、高斯混合模型(Gaussian Mixture Model, GMM)[8]和K 近邻算法(K Nearest Neighbor,KNN)[9]等，将以上方法相结合，如PCA-ICA[10]、PCASVM[11]等可以有效解决一些非线性问题。

由于化工过程数据的高维、非线性、非高斯和时变特性，工业过程中的故障检测与诊断仍然很困难。基于多元统计学和浅层学习方法，有两个主要问题：（1）特征提取过程需要专业知识和实践经验；（2）故障检测率仍不高。深度学习方法已被用于化工过程中的过程建模，其优异的性能引起FDD领域学者的关注[12-13]。卷积神经网络（CNN）是一种基于前馈神经网络的深度学习方法，它通过训练网络拓扑结构学习样本的分布情况。典型的卷积神经网络的卷积核是二维或三维的，卷积层以二维或三维数据的形式接收数据，同时也以三维数据的形式输出至下一层，保存了原数据的空间特征。在故障诊断任务中，Wang 等[14]应用二维卷积神经网络（Two-Dimensional Convolutional Neural Network，2D-CNN）提取化工过程数据的动态特征，其输入矩阵由一个时间窗内的采样点组成，矩阵的维度由采样时间和变量组成。此窗口操作会消耗时间和计算资源。一维卷积神经网络[15]将输入数据沿单一维度划分，无需进行加窗操作，更容易训练且计算复杂度较小。

在故障检测领域，传感器获取的数据是一维数据。如果选择二维卷积，则必须先进行加窗操作，将一维数据转换为二维数据。肖雄等[16]将原始时域信号数据转换成二维灰度图像，故障检测率达到98%。曲建岭等[17]采用一维卷积，以轴承的原始振动信号作为模型输入，同样也可以检测98%的轴承故障数据。Kiranyaz 等[18]采用自适应一维卷积神经网络对多电平转换器进行故障检测，计算复杂度较低，可以进行故障实时监控，故障识别率达99%。

虽然一维卷积是当前流行的故障检测深度学习方法，但它仍然存在一些局限性。卷积神经网络虽然可以提取数据的局部特征，但是提取数据全局特征的能力较弱。为了获得同时使用数据的全局和局部等有益特征，本文提出了一种基于并联结构的LSTM-CNN 结构（PLSTM-CNN），将卷积神经网络提取到的局部特征和LSTM 提取到的全局特征拼接起来，充分利用数据特征以提高模型的精度。

1 PLSTM-CNN 框架

1.1 一维卷积神经网络（1D-CNN）

卷积神经网络是目前广泛研究的深度学习算法之一，具有局部连接、权值共享和下采样等特点。1D-CNN 与经典CNN 区别在于卷积核的维度，近年来被广泛应用于时间序列的特征提取问题中。

一维卷积操作如图1 所示，其数学模型如式（1）所示：

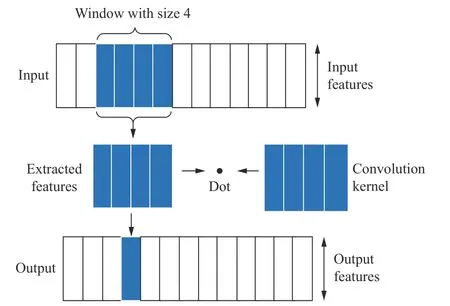
图1 维卷积操作Fig.1 One-dimensional convolution operation

其中：Hi为第i层输入特征量；⊗ 代表卷积运算；Wi和bi分别表示第i层卷积核的权重和对应的偏置；f代表激活函数，此处为Relu 激活函数，该函数具有良好的非线性表达能力。

池化层又称为子采样层。子采样层依据规则对特征图进行下采样，对卷积后的特征量进行降维以减少CNN 内部的参数和计算量，同时抑制网络过拟合。

1.2 一维稠密卷积神经网络

为了缓解网络深度引起的梯度爆炸问题，稠密卷积神经网络[19](Dense Convolutional Neural Network,DCNN)在残差网络结构的基础上进一步连接每一个子层，使得网络每一层输出用作后一层的输入，以保证最大程度上的特征重用，缓解了网络层数增加带来的梯度消失和梯度爆炸问题，使网络信息流动更加流畅。

假设网络层数为N，则DCNN 共包含有N(N+1)/2个连接。第n层的输入为前面所有层的特征映射，如式（3）所示：

其中：[x0,x1,···,xn-1] 表示第 0,1,···,n-1 层中的特征映射；H(·) 表示归一化线性修正单元、Relu 激活函数、池化操作以及卷积等函数变换。

因为DCNN 中各个卷积之后都会输出K个通道的特征图，重复使用特征会使输出通道维度非常大，所以在DCNN 内部结构中增加了一个核为1 的卷积层，以减少计算量并提高特征效率，如图2 所示为DCNN 的结构，其中BN 为批量归一化层。

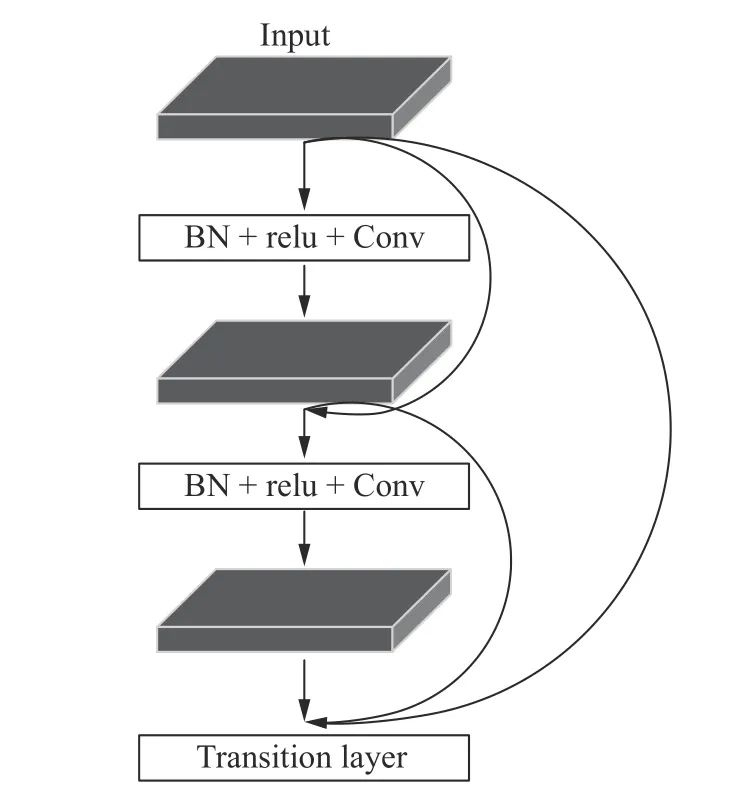
图2 稠密网络结构图Fig.2 Dense network structure diagram

1.3 长短时记忆网络

循环神经网络[20]（Recurrent Neural Network，RNN）表示当前的输出不仅依赖于当前的输入信息，还依赖于之前的输出信息。长短时记忆网络[21](Long and Short-Term Memory Neural Network，LSTM)是RNN的一种变体，它通过门单元的结构实现了自循环权重变化，可以有效缓解梯度消失和梯度爆炸的问题，更有利于提取时间序列的全局数据特征。

LSTM 网络以一种特殊的结构进行交互，网络包含：输入数据xt、输出门Ot、保持存储单元随时间(t)状态的遗忘门ft、影响记忆信息的输入门it、决定记忆和遗忘信息的存储单元Ct和调节信息流入或流出的非线性门控单元，其结构如图3 所示。

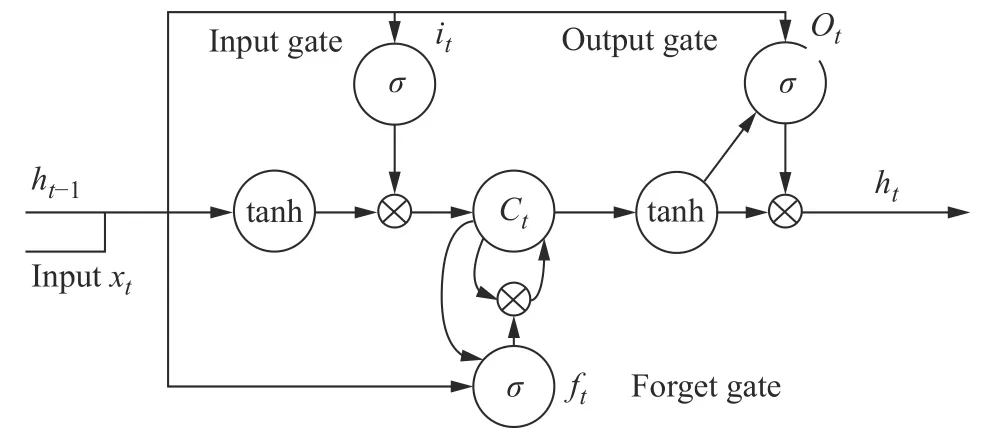
图3 LSTM 结构Fig.3 LSTM structure

LSTM 网络信息主要通过3 个门结构选择：输入门、遗忘门和输出门。式子(4)～(9)为LSTM 单元执行的过程：

其中：Wf、bf分别是输入数据和遗忘门之间的权重和偏置矩阵；Wc、bc分别是输入数据和存储单元之间的权重和偏置矩阵；Wo、bo分别是输入数据和输出门之间的权重和偏置矩阵；tanh 是双曲正切激活函数；σ 是Sigmoid 函数；◦ 是特殊运算符号；ht-1是t-1时刻的隐藏状态；xt是t时刻输入特征序列；ft可以清除来自存储单元的信息；输出门Ot根据当前时刻输入xt和前一时刻隐藏状态ht-1计算即将到来的数据信息。

2 基于PLSTM-CNN 的化工过程故障诊断方法

本文设计了一种基于PLSTM-CNN 网络的故障诊断方法。框架如图4 所示。

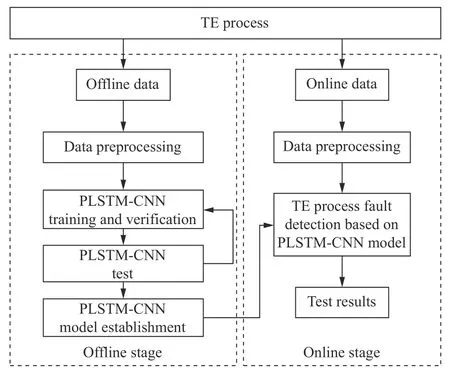
图4 基于PLSTM-CNN 故障诊断方法Fig.4 Fault diagnosis method based on PLSTM-CNN

本文提出的PLSTM-CNN 的故障诊断方法, 分为离线建模和在线检测两个步骤。

离线建模阶段包括以下步骤：

（1）采集不同工况（正常工况和故障工况）下TE（Tennessee Eastman）过程的输出数据，包括正常数据和20 种故障数据；

（2）数据预处理，首先对数据的变量按照最大互信息排序，然后归一化、标注对应的类别，最后划分为训练集和测试集；

（3）设计适用于TE 过程故障诊断的PLSTMCNN 网络结构；

（4）训练PLSTM-CNN 模型，直到模型在训练集上故障检测率和故障漏报率达到最优效果；

（5）测试PLSTM-CNN 模型，观测该模型在测试集上的泛化能力，若满足故障检测率和故障漏报率的要求，将该模型部署在在线检测阶段，不满足则调整参数重新训练、测试模型。

在线检测阶段包括以下步骤：

（1）在线采集过程数据，包括正常数据和20 种故障数据；

（2）同样地，对数据进行预处理；

（3）将在线数据输入到PLSTM-CNN 模型，模型输出每个在线样本的检测结果；

（4）如果诊断结果与专家经验的判断存在差异，则需要用新模型或新数据重新训练模型。

3 实验结果

3.1 TE 仿真平台

TE 过程是实际工业过程的仿真模型，其数据集广泛用于FDD 的研究。本文使用修订版的TE 过程模型，该过程包括41 个测量变量、12 个过程操作变量[22]。我们选择20 种故障与其他算法进行比较。

采样周期设置为3 min，正常状态下运行500 h，采集10 000 个正常样本。在20 种故障的模拟中，模拟器先正常运行10 h，然后引入相应的故障，再继续运行10 h。通过这种方式，每次模拟都收集了10 h的故障数据（200 个故障样本）。仿真平台在故障6 状态下运行7 h 后停机，故障6 只有7 h 的数据。为了使故障数据多样化，在10 种不同的初始状态下，每种故障重复模拟10 次。仿真平台共收集50 000 个样本数据，其中正常样本10 000 个，每种故障2 000 个样本。选择70%的数据进行训练，20%的数据进行测试，10%数据进行验证。

3.2 数据分析

为了分析各类故障样本与正常样本之间的相关性，利用每类故障数据与正常数据之间的互信息（Mutual Information，MI）进行度量。互信息[23]定义如式（10）所示：

其中：g,h分别是x,y方向上的线段数；p(x,y) 为变量x,y的联合概率分布。因为p(x,y) 计算较为复杂，采用随机划分样本集的散点图方法进行逼近。MI 在二维空间的横轴和纵轴方向上划分一定数量的区间，用散点图表示两个变量，计算散点落在各个方格中的概率，如图5 所示。

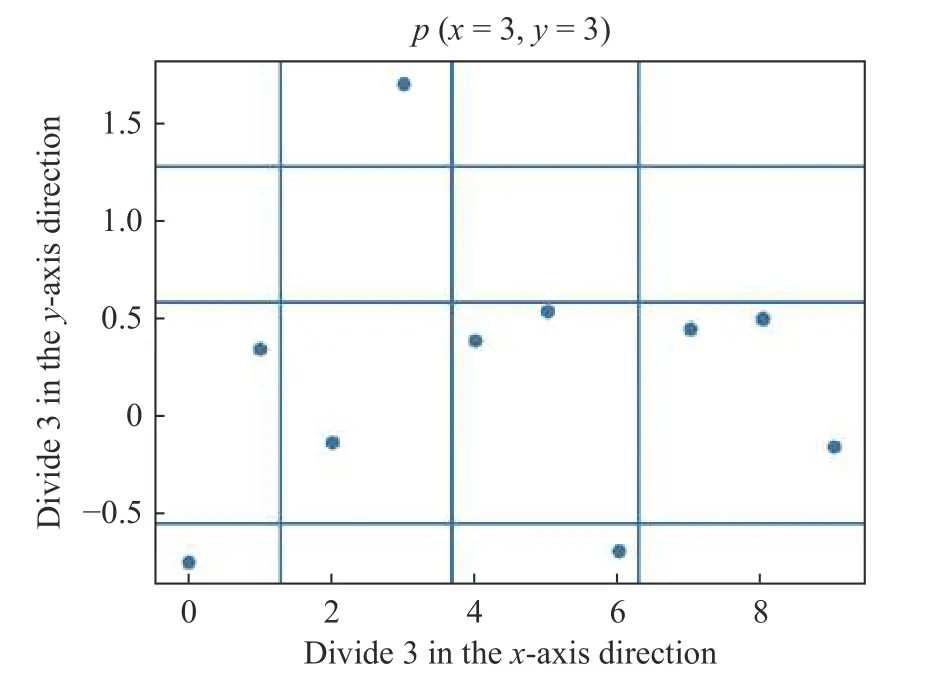
图5 MI 网格计算方法Fig.5 MI grid calculation method

正常数据与20 种故障数据之间的互信息值见图6，故障03、故障05、故障09、故障15 和故障16 这5 种故障数据与正常数据之间的互信息值显著高于其他，说明这5 种故障在数据表现上与正常样本相近，混淆程度较高。因此可以推测，这5 类故障比其他类型的故障检测难度更大。

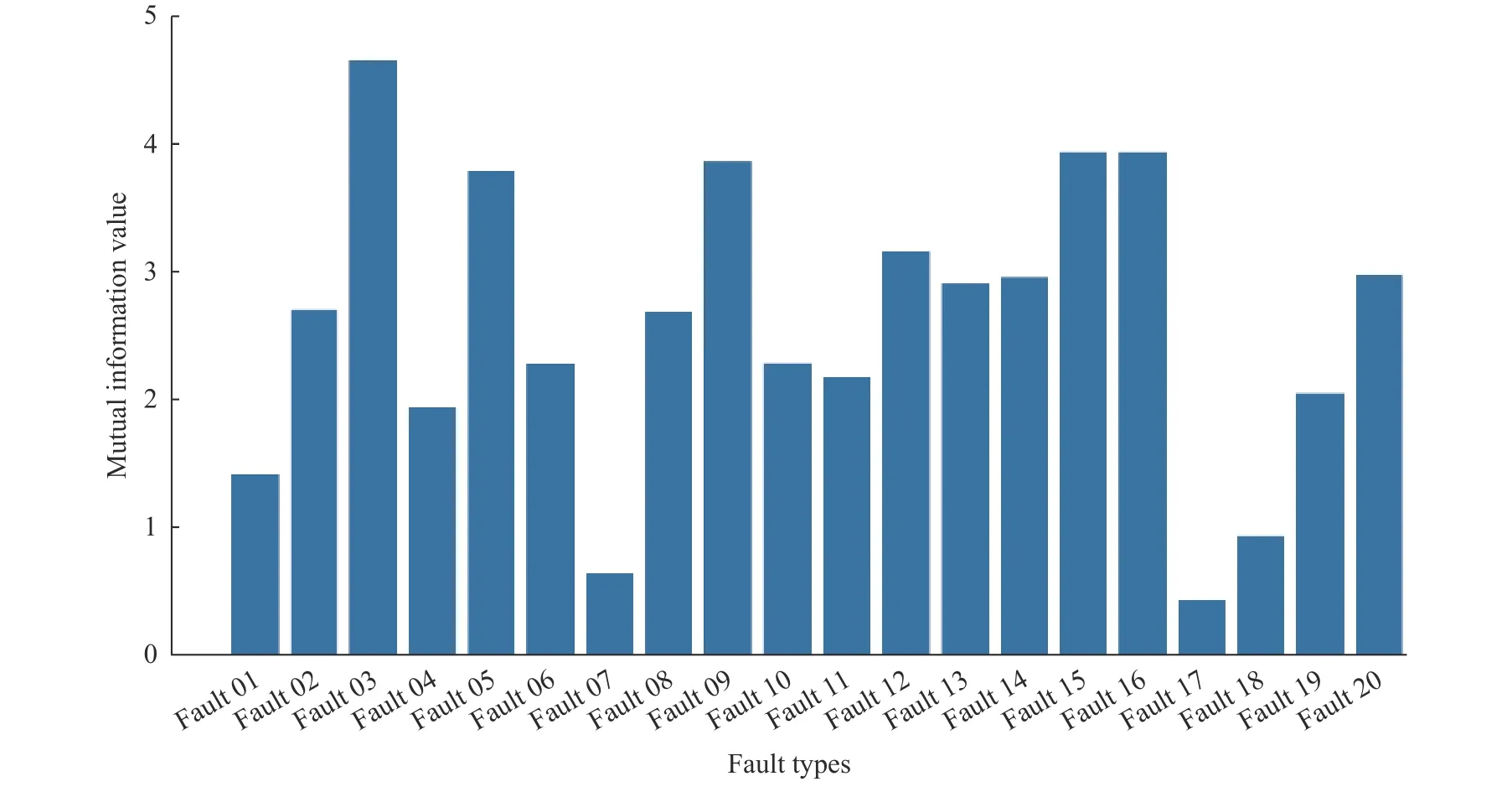
图6 正常数据与故障数据互信息值Fig.6 Mutual information value of normal data and fault data

3.3 数据预处理

数据预处理包括变量过滤和排序、数据归一化、打标签以及训练和测试集的划分。在TE 过程中，XMV(5)（压缩机循环阀）、XMV(9)（汽提塔蒸汽阀）和XMV(12)（搅拌机速度）在模拟过程中是固定值，因此这3 个变量被剔除。

3.3.1 变量排序 在深度学习任务中，一旦文本的前后顺序改变或图像语义扰乱，学习就很难有效果。在化工过程变量排序问题上，同样存在这样的问题。最大信息系数（Maximal Information Coefficient,MIC）是Reshef 等[24]提出的一种用于从信息论的角度测量随机变量之间的线性和非线性的相关程度的方法。采用这种方法计算变量之间的互信息系数对变量进行排序，从而使得变量更有规律，提高样本的局部相关性。计算两个变量之间的互信息系数，并按照相邻变量之间的互信息系数最大的方式对变量进行排序。最大互信息系数定义见式（11）：

其中：g,h是在x,y方向上划分格子的线段数；B取数据量的0.6 次方；a,b是在x,y方向上的划分格子个数。

因为故障3 和9 与TE 过程中的进料D 的温度有关，所以选择变量XMEAS(9)（反应器温度）为初始变量，并根据计算最大互信息系数公式对其余50 个变量重新排序，按照该顺序排列成1×50 的输入样本，并获得变量的排序顺序如图7 所示。

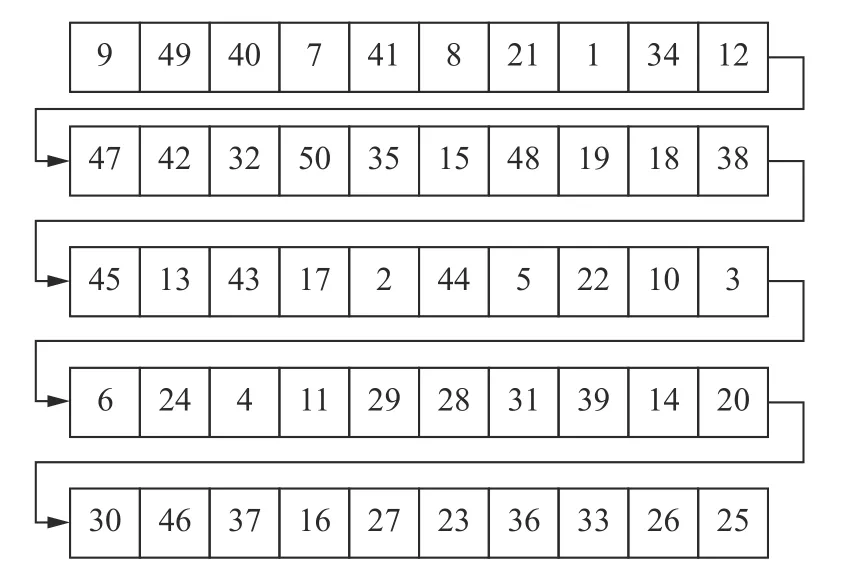
图7 变量排序后的格式Fig.7 Sorted variable order

3.3.2 归一化 由于化工过程数据的量级和维度并不完全相同，为了避免不规则数据带来的数值问题，统一评价标准，使网络更快收敛，采用Z-score 归一化预处理方法，其公式如式（12）所示。

其中：x是未归一化的样本数据；x¯ 是样本均值；S(x)是标准差；Z(x) 是标准化后的数据。

3.3.3 打标签 One-Hot 编码是多分类问题中标签处理的标准操作。具体操作是将其转换为数组，其中相应标签种类的列为1，其余为0，如故障10 的One-Hot 编码为：[0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0]

3.4 模型结构

由于每个训练样本为1×50 的短序列，较大的卷积核不适合，较小的卷积核可以防止特征丢失。选用卷积层滤波器为32 个，卷积核为3。LSTM 有16 个单元，Dropout 为0.8。PLSTM-CNN 网络模型如图8 所示。

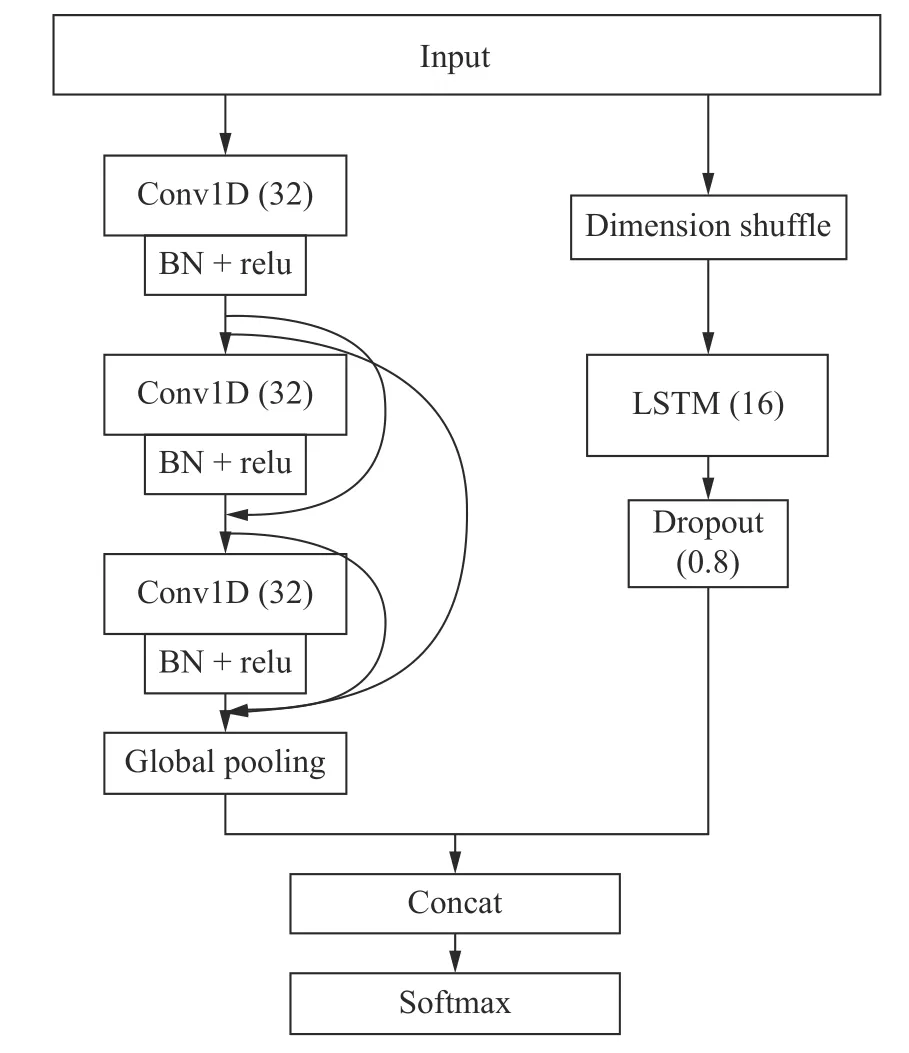
图8 PLSTM-CNN 网络模型Fig.8 PLSTM-CNN network model

图8 所示的这种并行的网络结构最大程度地避免了特征丢失，保留了数据特征的全局和局部信息；残差结构增强CNN 稳定性并且减少资源的占用；批量归一化层（Batch Normalization，BN）加速网络训练速度，抑制网络过拟合；左边的全局平均池化层将降维后的特征图与右边的网络特征图拼接，最后送到分类层。

建立模型后，将训练集输入到模型中进行训练。在训练过程中，超参数的设置会影响模型的收敛效果和预测精度，主要包括：学习率、迭代次数、批次大小、激活函数、隐含层的数目和单元数、优化器和损失函数。

将交叉熵损失函数（Categorical Crossentropy）用作损失函数。该损失函数可以避免更新权重较慢的问题，有利于模型收敛。计算公式见式（13）：

其中：t是正确类别；q(xt) 是预测正确类别的概率。

选择Nadam 作为模型的优化器。它是一种带Nesterov 动量项的自适应学习率优化算法。该算法训练前期和中期收敛速度快，计算效率高，训练后期不容易过拟合，适合解决大数据或大参数的优化问题。学习率设置为0.002。

用于训练的batchsize 设置为256，epochs 设置为100。batchsize 指每次迭代的一次向前或向后遍历中的样本数量，epochs 指遍历整个数据集的次数。

4 实验结果分析

4.1 故障检测结果

为了展示故障检查结果和评估模型性能，使用故障诊断率（Fault Diagnosis Rate，FDR）和误报率（False Positive Rate, FPR）两个指标评估模型性能。FDR 和FPR 定义为：

其中：TP(True Positives)表示实例是正类并被预测成正类的个数；FN(False Negative)表示正类被预测成负类的个数；FP(False Positives)表示实例是负类被预测成正类的个数；TN(True Negative)表示实例是负类被预测为负类的个数。

为了验证所提方法的性能，将PLSTM-CNN 模型、2D-CNN 模型、LSTM 模型在测试数据上的结果进行比较，结果如表1 所示，表中基于PLSTM-CNN模型平均故障检测率达0.91。

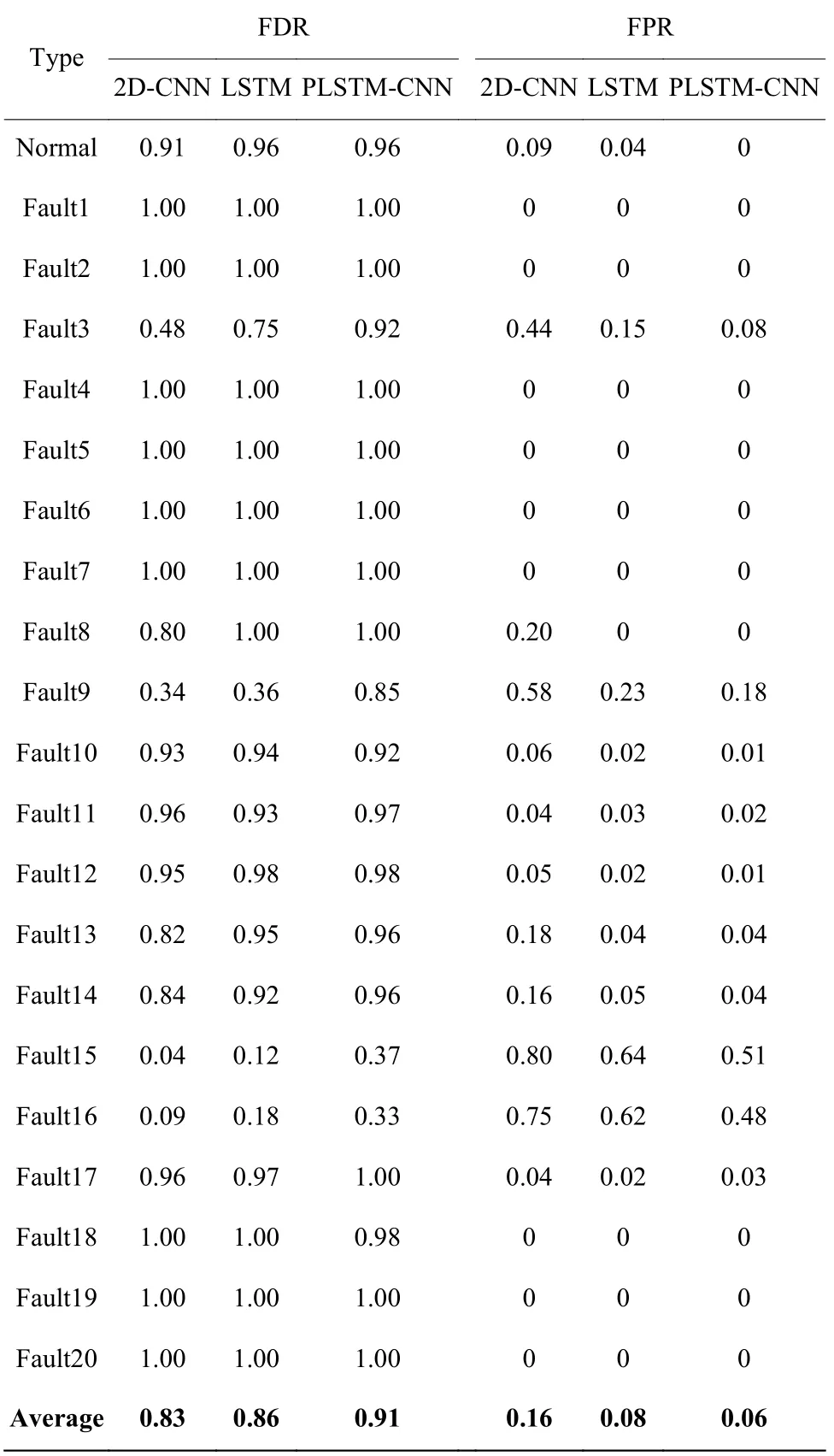
表1 故障检测结果比较Table 1 Comparison of fault detection results

我们发现不同故障的分类精度差异很大。基于PLSTM-CNN 的故障9 的检测率（FDR）小于0.90，故障15 和16 检测率低于0.50。此外，其余17 种故障检测率均高于0.90，其中故障1、2、4、5、6、7、8、17、19、20 的检测率为100%。因此，PLSTM-CNN 可以有效隔离大部分故障，只有少数故障表现不佳。通过对表中数据的分析，发现故障3、9、15、16 的准确度较低是由于它们之间的混淆程度较高，这与前文互信息计算的结果相符合。本文提出的PLSTMCNN 模型充分利用原数据局部和全局特征，在混淆程度较高的故障3、9、15、16 中故障检测率和误报率均优于2D-CNN 和LSTM 模型。因为故障3 和故障9 都与进料D 的温度变化有关，所以本文以反应器温度为初始变量，按照最大互信息系数的方法重新排列变量，进一步提高了对故障3 和9 的故障检测率。故障15 和16 混淆程度过高，目前还没有行之有效的故障检测方法。

4.2 特征可视化

在收集实验结果和模型之后，为了对模型学习到的特征图可视化，引入了t 随机邻居嵌入（tdistributed Stochastic Neighbor Embedding，t-SNE）方法，该方法由van der Maaten 和Hinton 于2008 年提出，可将高维数据投影到二维平面[25]。

从测试集中随机选择21 种类别4 200 个样本，包括20 种故障样本和1 种正常样本，并对样本进行可视化。在图中每个点代表一个样本，为了方便观察分类效果，用数字和颜色代表其实际的类别标签，如灰色标签为“13”代表故障13 样本。分别对输入层和分类层的特征进行可视化，其结果如图9 所示，左图为输入数据可视化结果图，右图为输出层t-SNE 的可视化结果图。

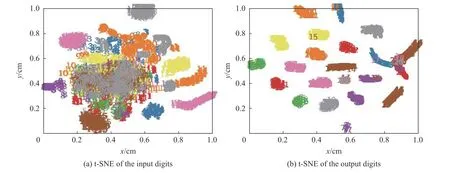
图9 基于t-SNE 的故障诊断可视化Fig.9 Fault diagnosis visualization base on t-SNE

4.3 对比实验

4.3.1 平均故障检测率对比 为了进一步对比串行与并行网络模型的故障检测能力，在上文数据集的基础上设计了传统串行网络结构，结构如图10 所示。故障检测实验效果如图11 所示。

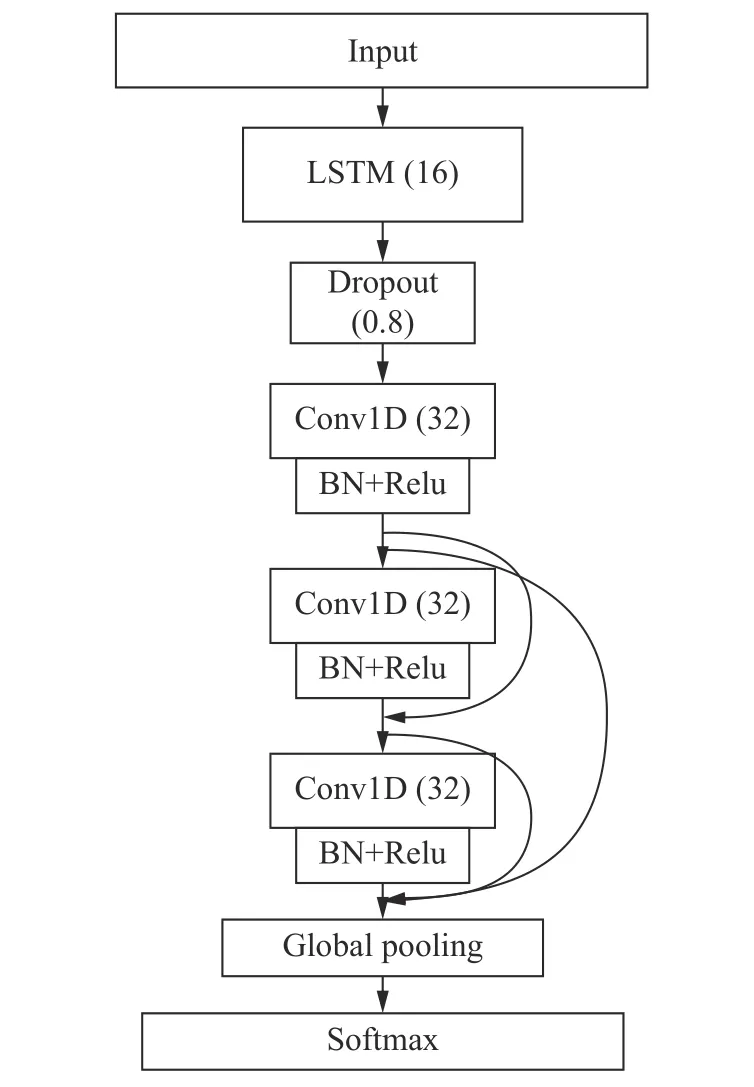
图10 串行LSTM-CNN 网络结构Fig.10 Serial LSTM-CNN network structure

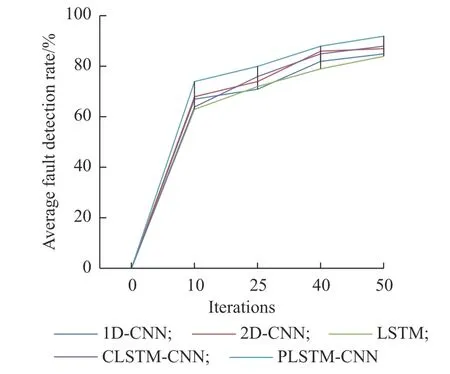
图11 平均故障检测率Fig.11 Average fault detection rate

PLSTM-CNN、串行长短时记忆网络和卷积神经网络（CLSTM-CNN）、LSTM、1D-CNN 和2D-CNN模型的平均故障检测率分别为92.13%、89.54%、84.08%、84.80%和85.78%。这表明PLSTM-CNN 相比于CLSTM-CNN 具有更好的故障检测效果。

4.3.2 模型推理和推理时间对比 表2 示出了多种模型训练、推理时间的比较。PLSTM-CNN 模型训练每个epochs 需消耗4.20 s，训练100 个epochs 仅需消耗7 min。其训练速度较快的原因主要是：考虑到故障监测的实时性，本文卷积层选为一维卷积，其参数较少，在相同网络和超参数的条件下，计算时间较短，但会丧失部分精度。

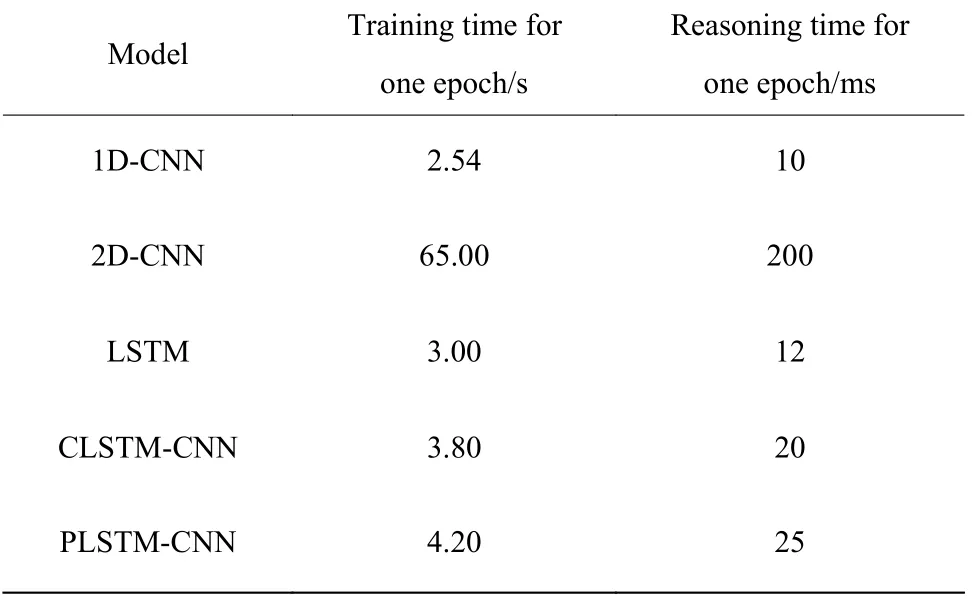
表2 训练、推理时间比较Table 2 Comparison of training and reasoning time

同时，训练深度二维卷积网络通常需要特殊的硬件设备，例如云计算或GPU 加速等。但1D-CNN可以在普通的计算机的CPU 上实施，其低计算要求和紧凑型的结构非常适合实时监测和低成本应用。

4.3.3 小样本平均故障检测率对比 考虑到实际化工过程故障样本稀少，实验将降低每类故障样本数量。设置采样时间为3 min，正常状态下运行100 h，收集到正常样本2 000 个。对20 种故障的仿真中，模拟器先正常运行10 h，再引入相应的故障，然后继续运行10 h。这样，每次模拟收集10 h 的故障数据（200 个故障样本）。每种故障类型的仿真在10 种不同的初始状态下重复10 次。仿真平台共收集42 000个样本数据，其中正常样本2 000 个，每种故障2 000个样本。选择70%的数据进行训练，20%的数据进行测试，10%数据进行验证。实验结果如表3 所示。

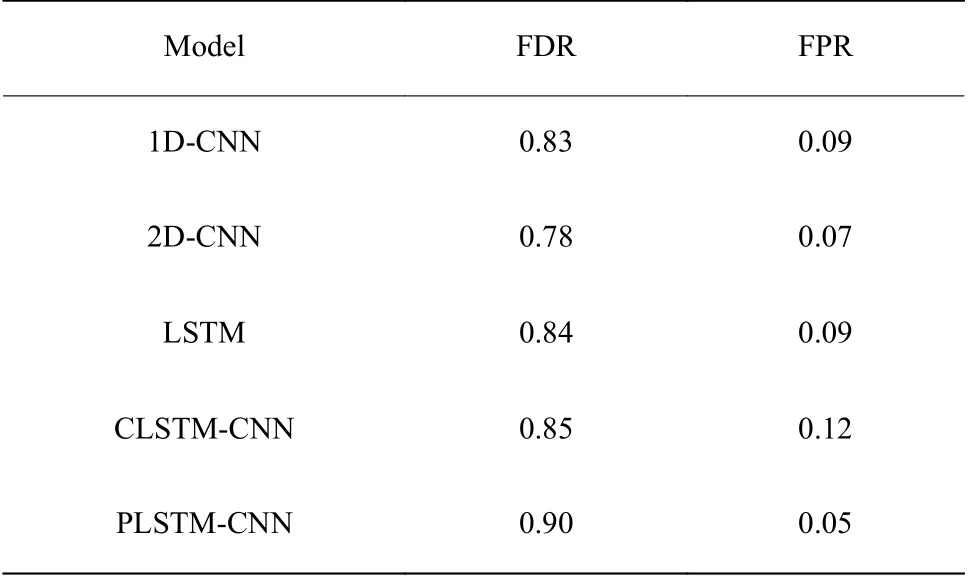
表3 小样本平均故障检测率Table 3 Average fault detection rate of small samples

2D-CNN 需要大量训练样本才能保证精度，而1D-CNN 在小样本数据集上仍表现良好。PLSTMCNN 在小样本数据集上仍能保持较高精度，其网络结构比串行网络更稳定。

5 结 论

本文提出了一种基于PLSTM-CNN 网络模型的化工过程故障检测的方法，模型由LSTM、一维稠密卷积层、一维全局池化层和Dropout 层构建，可以有效提取故障数据的局部和全局特征；经过数据分析和基于最大信息系数方法的变量重排序后，数据分布更规则，易于训练。将该方法应用于TE 化学过程的故障检测，比较了PLSTM-CNN、CLSTM-CNN、LSTM、2D-CNN 的故障检测结果。实验结果表明，PLSTM-CNN 的故障检测准确率和误报率明显优于其他方法。而对于难以检测的故障3 和9，PLSTMCNN 模型表现仍然良好。

本文提出的PLSTM-CNN 故障诊断方法具有较高的故障诊断准确率和较好的可靠性，更容易区分不同的故障类型。但是，该方法仍存在普遍深度学习网络的局限性，网络中任何参数的变化都会影响模型的质量，很难找到最优模型；另外，当参数恒定时，每次训练的结果也可能有误差，这些问题是作者今后的研究方向。