基于稀疏D-vine Copula 的建模方法及其在过程监测中的应用

邱穗庆，李绍军

（华东理工大学能源化工过程智能制造教育部重点实验室, 上海 200237）

现代工业过程规模日趋扩大，生产系统也日趋智能化和复杂化，这大大提升了生产效率，但也增加了系统的不确定性和潜在的安全隐患。过程监测技术在保证系统安全生产方面扮演着关键角色[1-2]。随着大规模数据采集和处理技术的不断发展，基于数据驱动的过程监测方法有着巨大的应用前景[3]，其中多元统计过程监测[4](Multivariate Statistical Process Monitoring, MSPM)方法通过挖掘潜在变量信息建模，在工业过程监测领域得到了广泛应用。主成分分析(PCA)[5]和偏最小二乘(PLS)[6]方法先将数据投影到较低维的子空间，再计算T2和SPE 指标来区分正常和异常状态，是MSPM 的典型代表。PCA 和PLS 这两种方法都默认过程变量线性相关且服从高斯分布，但在实际过程中，这两个条件往往难以满足。针对这个问题，一系列改进和新方法逐渐被提出。为应对非线性问题，核主元分析(KPCA)[7]、核偏最小二乘法(KPLS)[8]等方法陆续被提出。另外，Kano等[9]将独立主元分析(ICA)引入到过程监控领域处理数据的非高斯信息。Yu 等[10]提出有限高斯混合模型(FGMM)，从分布的角度解决了非高斯问题。然而，大多数现有MSPM 方法都是以降维解耦或高斯假设思想为基础。因此，从描述数据间相关性角度出发，通过直接刻画复杂过程变量之间的相关性行为来建立过程监测模型，具有极高的研究前景。

近年来，作为一种相关性建模工具，Copula 函数在金融和气象等领域[11-12]得到了广泛应用。Copula函数将联合分布函数与边缘分布及其相关性结构联系起来，直接根据数据间的复杂相关性信息建立数据分布模型，能够有效处理数据间的非线性非高斯信息[13]。然而，利用传统多元Copula 函数建立高维数据相关性模型时，其参数优化过程繁琐且低效，缺乏灵活性。为避免复杂的优化过程，Joe[14]提出Vine Copula 分解方法。借助Vine 结构，多元Copula函数可以分解为一系列二元Copula 函数的组合形式，实现了将复杂多元相关性建模问题转变为二元Copula函数的优化问题。Vine Copula 理论的改进与发展促进了它在工业制造领域的应用。Ren 等[15]将C-vine模型引入到过程监控领域，构建广义贝叶斯推断概率检测指标，实现了对非线性非高斯工业过程的实时故障监测。周南等[16]通过核密度估计选择最优的Copula 函数参数。崔群等[17]借助伯恩斯坦多项式优化了D-vine Copula 参数估计过程，并应用到过程监测领域。二元Copula 种类繁多，可以针对不同的相关性结构灵活选择，重点在于如何估计和优化二元Copula 的结构和参数。目前最常用的优化准则是基于最大伪似然估计的BIC(Bayesian Information Criterion)和Akaike 信息准则。然而，由于Vine 结构优化是从第1 棵结构树开始依次估计二元Copula，按照常规的优化准则，估计误差容易在树中累积，导致较高层次树中的估计结果可靠性较差，进而影响整个Vine Copula 模型的性能。实际上，在较高层次的树中往往只含有少量的相关性信息[18]。此外，虽然Vine Copula 分解可以使得每个二元Copula需优化的参数个数不超过两个，但整个Vine 模型需优化的参数数量随着数据维数的增加呈现二次增长。这会大幅增加高维数据的计算负担，很难保证模型的实时性。

C-vine 和D-vine 是最常用的两种Vine 结构。1 个m元变量的Vine 结构包括m-1 棵结构树和m(m-1)/2 条边(二元Copula)，每条边连接2 个节点（变量）。相较于C-vine 的星型分解结构，水平结构的D-vine 有着简单、稳定且易于建模的优势[19]。为减少模型的计算时间和估计误差在Vine 结构中的累积，本文通过改进的BIC(mBIC)[18]优化准则对D-vine结构和参数进行估计和优化，建立一种稀疏D-vine Copula(SDVC)过程监测模型。该模型修正了每个二元Copula 的先验概率，对不同层次结构树分配不同参数的伯努利分布先验，使得高层次树中有更大概率优化为独立二元Copula，大大减少了需优化参数的Copula 个数。另外，在现有基于Vine Copula 的过程监测模型中，Vine 结构的节点次序都是根据与根节点的相关性程度决定的，该方法更适合于存在根节点的C-vine 星型结构[15]。本文Vine 结构的节点次序只与各节点间的相关性总和大小有关，不受制于根节点，更适用于水平结构的D-vine。在建模阶段，首先根据mBIC 准则对第1 棵树中二元Copula 进行拟合优化，后一棵树的二元Copula 根据前一棵树的优化结果逐级优化。通过mBIC 不仅可以对高层次树进行一定程度的稀疏，还可以达到降低计算量和避免过拟合的效果。核密度估计方法被用于估计各变量的边缘概率密度函数(Probability Density Function，PDF)。针对工业生产过程，利用SDVC 模型并结合高密度区域(HDR)和分位数理论构建非线性非高斯态广义局部概率(GLP)监测指标。SDVC 模型在田纳西-伊斯曼(Tennessee-Eastman，TE)和醋酸脱水过程中的应用，验证了该模型能够取得良好的监测效果。

1 D-Vine Copula 理论及其建模方法

Copula 是以服从均匀分布U(0,1)的分布函数为自变量而构成的多元分布函数，它实现了用边缘分布及其相关性结构(Copula 函数)替代联合分布。Skalr[20]提出，m维随机变量X=(X1,X2,···,Xm)T的联合概率分布可以用对应维数的Copula 函数表示：

其中C(·)表示Copula 函数，ui=Fi(xi) (i=1,2, ···,m)为对应变量的边缘分布函数，其满足：

其中fi(xi)表示xi的边缘PDF。对式(1)两边同时求导，得到式（3）：

由式(3)可见，多元随机变量的联合分布由各变量的边缘分布及其相关性结构共同决定。边缘分布易于求取，多元Copula 密度函数通常由极大似然法估计获得。然而，一个m元Copula 函数需要优化的参数个数远远大于m，当数据维数过高时，容易出现“维数灾难”。Joe[14]提出Vine Copula 分解结构，将多元Copula 函数分解为一系列二元Copula 函数的组合形式。

1.1 D-vine Copula

Vine Copula 的基本思想是将一个m元Copula函数分解成m(m-1)/2 个二元Copula 函数的组合形式。由此高维变量间相关性结构的优化问题转化为一系列二元Copula 的参数估计问题(每次需优化的参数为1～2 个)[21]，这对处理高维非线性非高斯数据提供了极好的解决思路。D-vine 凭借其简单稳定的结构特点，广泛运用于各个研究领域。对于m元随机变量，采用D-vine Copula 分解形式可将联合概率密度分布模型表示为：

其中，θj,j+i|j+1:j+i-1表示对应二元Copula 函数的参数。需要注意的是，式(4)是按照从低到高层次树的顺序依次优化估计，其中条件分布项的计算方式为：

其中，xD表示条件向量集，v是属于xD的一个向量，xD-v为除v之外的向量集。为便于理解，图1 展示了五元变量的D-vine 图解模型。D-vine 图解模型是由若干个节点和边组成的一系列水平无环连接图，每个连接图称为D-vine 的一棵树。一个五元D-vine 结构包含4 棵树、10 条边，Copula 密度函数由各条边依次累乘获得。因此，只要优化出所有二元Copula 函数就能快速获得联合概率密度分布模型。

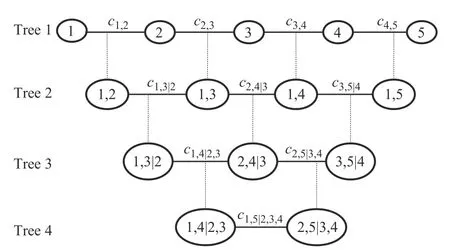
图1 五元D-vine 图解模型Fig.1 Graphical model of five-dimension D-vine

1.2 D-vine 模型构建

D-vine 是水平结构，节点次序决定了整个Vine结构框架。根据Ren 等[15]的相关研究，首先将与其他节点秩相关系数总和最大的节点视为根节点排在首位，再根据其他节点与根节点的秩相关系数大小按降序依次编号。

二元Copula 种类繁多，初步确定D-vine 结构后需要对二元Copula 具体类型和参数进行估计优化，基于极大伪似然估计的BIC 准则是常用的一种。

式（6）右边第1 项表示每个二元Copula 包含相关性信息量的对数似然函数，第2 项表示每个二元Copula的复杂度，n和m分别为样本数量和维数，是每个二元Copula中的非零参数个数，cpair是二元Copula 密度函数，θj,j+i|j+1:j+i-1为待优化参数。最终优化出的BIC值越小，说明模型越精确。

在估计D-vine 模型时，首先估计低层次树中的二元Copula，在此基础上逐级估计高层次树，最终确定完整的D-vine Copula 模型。这一优化过程决定了在低层次树中的估计误差很容易累积到高层次树中，导致较高树中的二元Copula 模型可靠性较差，整个优化过程计算量也很高。并且，通常都是在低层次树中捕获强依赖关系，而在较高层次的树中描述的条件相关性逐渐减弱，包含的信息量减少[22]。

针对以上问题，Kovács 等[22]提出了对Vine 结构的截断，直接移除Vine 结构中的高层次树，避免了估计误差的累计，降低了计算量。在工业过程中，变量间的相关性复杂度高，有的变量间为弱相关或不相关，截去这一部分对模型整体影响不大；但有的变量则呈现强相关，直接截断高层次树可能会导致一部分重要信息丢失。通过mBIC 对D-vine 进行优化，可以让高层次的树变得更加稀疏(包含更多独立二元Copula)。即在更高层次的树中，二元Copula更倾向于优化成独立状态。这一方面能在一定程度上减少估计误差，提高模型可靠性；另一方面，由于独立二元Copula 函数不需要优化参数，还可以降低建模计算量。

2 SDVC 过程监测模型

2.1 稀疏D-vine Copula 模型估计

为确定更适合于D-vine 结构的节点次序，采用如式（7）方式（第1 棵树）计算：

BIC 是Vine 估计和优化的常用指标，它是在假设所有二元Copula 选择都是等概率先验的情况下导出。当过程数据维数较高时，为减少估计误差在高层次树中的累积，可以适当对高层次树的Vine 结构进行稀疏。mBIC 优化准则可以有效地完成这一任务，它在BIC 准则的基础上改进了先验概率，具体是给每个二元Copula 分配一个非独立的先验概率。这里让该先验概率服从伯努利分布（参数为 ψe），其中第t棵树中的参数 ψe=(0 ＜ψ0＜1) 。由此整个Dvine Copula 模型的先验概率为：

其中，qt表示在第t棵树中非独立二元Copula 的数量。根据先验概率，可以得出mBIC 准则的定义：

其中，等式右边新添的第3 项由先验概率决定。根据ψ0的取值范围可知，是一个递减序列。这意味着在更高的树中，mBIC 准则对非独立二元Copula 的惩罚比BIC 准则更严重，更倾向于将二元Copula 优化成独立状态(待优化参数个数为0，Copula 密度默认为1)。这种估计方式可以使Vine 结构变得稀疏，方便处理高维问题。

在服从伯努利分布的先验概率条件下，随机变量qt服从参数为(m-t)和的二项分布。因此，在第t棵树中，非独立二元Copula 数量的期望值为

则稀疏D-vine 结构中非独立二元Copula 总数量q的期望值为

其中O(·) 表示求极大值。在常规的D-vine 结构中，qmax与m2有关，因此，通过设置合理的 ψ0，很容易获得稀疏的D-vine 结构，尤其是在数据维度m较大的情况下。

由于估计误差容易在Vine 结构树上累积，在越高层次的树中估计结果越不可靠，因此，应该越保守地选择模型，通过mBIC 让高层次的树变得稀疏，在一定程度上能减少估计误差。不同的 ψ0可以构建不同稀疏度的Vine Copula 结构，通常，设置 ψ0=0.9 是较为普遍适用的情况[18]。

2.2 边缘概率密度分布模型

由式(4)可知，多元变量的联合PDF 模型与Copula密度函数和各变量的边缘PDF 相关。对于已知分布类型的变量，其边缘PDF 参数可以根据数据轻易估计得出。否则，可以借助核密度估计此非参数估计方法。单变量核密度函数[24]表示为式（12）：

其中，K(·) 为核函数，满足K(u)du=1 ；z和zi分别表示单变量和估计样本；h为窗宽。

2.3 构建监测指标

通过稀疏 D-vine Copula 和核密度估计器获得训练样本的概率密度分布模型后，需要确定一个控制界限，若监测数据的概率密度值在界限内则将其视为正常，反之判定为异常。如果过程数据服从高斯分布，正常区域可通过马氏距离方便得出。然而，对于多元非高斯分布的情况，马氏距离不再适用。高密度区域(High Density Region , HDR)[25]是一种适用于任意分布的概率性度量区域。它能在给定概率δ的情况下，以尽可能精确的体积覆盖某一区域，该区域内每个点的概率密度值都大于或等于区域外的点。假设多元变量X的联合PDF 为f(x)，则HDR 代表了最小的1-δ区域，用数学公式表示为：

其中HDR(fδ)表示处于置信水平为1-δ的HDR 中的点集，fδ是f(x)的δ分位数。

利用HDR 计算控制界限关键在于获得fδ。因此，HDR 的概率估计问题等价为搜寻一维随机向量f(x)对应的分位数。引入密度分位数法(Density Quantile Approach, DQA)[25]估计HDR 的边界。定义计算得出的联合PDF 模型为Y=f(x)，HDR(fδ)=[α,β]，且f(α)=f(β)，则由式(13)可知fδ应满足如下关系：

其中P表示求取符合括号内条件的概率值。

可以利用样本数据Yi=f(xi) (i=1,2,···,n，其中n为样本数量)估计出fδ，实际上这里是利用样本分位数去估计随机变量Y的δ分位数fδ。

基于HDR 和DQA 提出适用于非线性非高斯过程数据的GLP 指标完成工业过程实时监测：

则求得GLP 指标为

DQA 方法所得结果是区间估计，首先对训练样本的联合PDF 值进行离散化处理，离散化步长为l，生成一张包含l个区间的密度分位数表(包含l+1 个置信水平和对应的l+1 个密度分位数值)。根据给定的控制限(CL∈(0,1))，l= [1/(1-CL)]，其中[]表示取整，求取GLP 的过程就是搜寻到其所在概率估计区间的问题，并将其设置为该区间上下界的均值。理论上只要l足够大，采用DQA 方法就可以实现对GLP指标任意精度的估计。对于控制限CL，若GLP ＜CL，则认为过程是正常状态，反之判定为出现异常。

2.4 基于SDVC 过程监测方法的建模流程

本文提出的SDCV 过程监测方法流程图如图2所示，整个过程包括离线建模和在线监测两个部分。

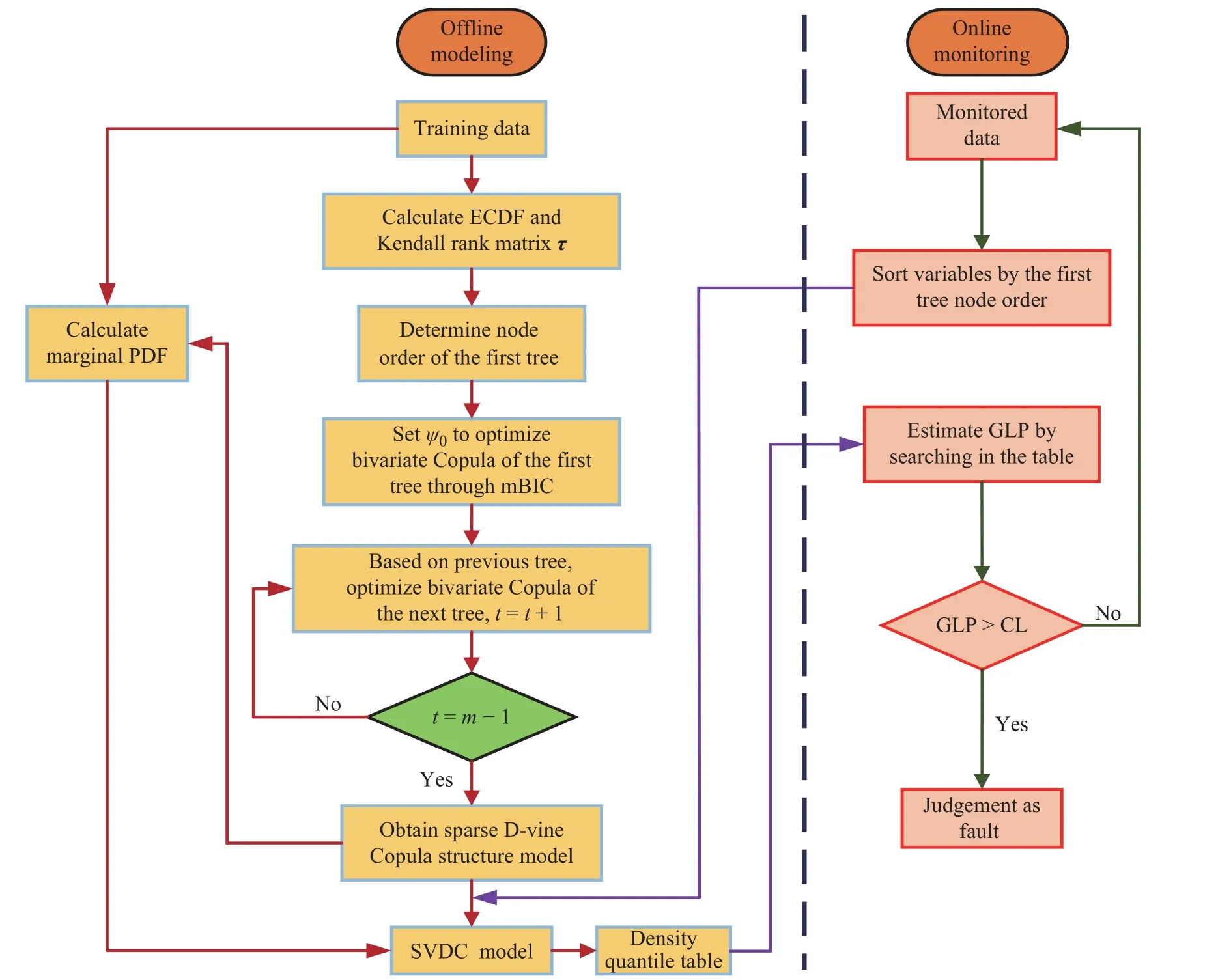
图2 SDVC 过程监控方法算法流程图Fig.2 Algorithm flowchart of SDVC monitoring approach

离线建模具体流程细节如下：

(1) 收集正常状态下的历史数据，通过式(12)计算随机变量xi(i=1,2,…,m)的m个边缘PDF，即fi(xi)；

(2) 利用样本数据计算各随机变量的边缘累积分布函数(ECDF)值和各变量间的Kendall 秩相关系数矩阵 τ ∈Rm×m；

(3) 根据式(7)与矩阵 τ 确定D-vine 模型中第1 棵树的节点顺序，得到第1 棵树结构框架；

(4) 给连接节点的边(二元Copula)分配服从参数为 ψ0的伯努利分布的先验概率，并利用第1 棵树中各节点对应的边缘累积分布函数优化各边对应的二元Copula 类型及其参数，计算每条边对应的mBIC值，选择使mBIC 为最小的二元Copula 及其参数；

(5) 对于第1 棵以外的树t，结合第t-1 棵树中已优化好的二元Copula 及条件分布函数，根据式(5)计算出第t层中所需要的条件分布函数作为新的节点(参考图1)；

(6) 给第t棵树中的边分配服从参数为的伯努利分布的先验概率，对第t棵树中的二元Copula进行估计，估计方法和流程与步骤(4)一致；

(7) 令t=t+1,流程返回至步骤(5)；当完整的稀疏D-vine 结构模型优化完毕，进入步骤(8);

(8) 结合步骤(1)计算出的fi(xi)以及优化出的稀疏D-vine 结构，通过式(4)得出最终的SDVC 模型；

(9) 利用SDVC 模型计算出训练样本的联合PDF模型f(x)，并确定CL，建立对应的密度分位数表。

在线监测具体流程细节如下：

(1) 利用SDVC 模型计算出实时监测数据的联合概率密度值，结合式(16)和式(17)，用DQA 计算出GLP 指标；

(2) 判断GLP 是否超限，若GLP ＜ CL，则是正常状态，反之判定为出现异常。

3 应用实例

为评估所提出方法的监测性能，以TE 和醋酸脱水过程作为实例，将SDVC 方法监测结果与PCA、KPCA 和D-vine 方法进行对比和讨论。

3.1 TE 过程

TE 过程是由美国Eastman 公司根据实际的化工反应过程开发的测试仿真系统，在工业过程监测领域是一个常用的应用实例。TE 过程是一个高度复杂的非线性非高斯系统，主要包含5 个操作单元：反应器、冷凝器、压缩机、分离器和汽提塔，其过程数据集包含22 个过程变量、19 个成分变量和11 个操纵变量以及21 类故障信息。每类故障数据均为960 组，且故障都是从第161 个样本点引入并维持到最后时刻。

本文利用正常状态下的960 组数据，通过22 个过程变量，建立PCA、KPCA、D-vine 和SDVC过程监测模型。为了保证实验的公平性和有效性，置信水平均设置为0.99。设置SDVC 模型中伯努利分布参数 ψ0=0.9，主成分的方差贡献率为85%。图3 所示为TE 过程的稀疏D-vine 和D-vine 结构信息矩阵。右上角为稀疏D-vine 结构的信息矩阵，第1 行对应第1 棵树的节点顺序，剩余行中的数字分别对应各Vine 结构树中的二元Copula 种类，如0 代表独立Copula，1 代表高斯Copula[26]；Ti表示第i棵Copula结构树。左下角为D-vine 结构信息矩阵，各位置信息与右上角斜对称，如第2 列中的数字表示D-vine第1 棵树的优化结果。

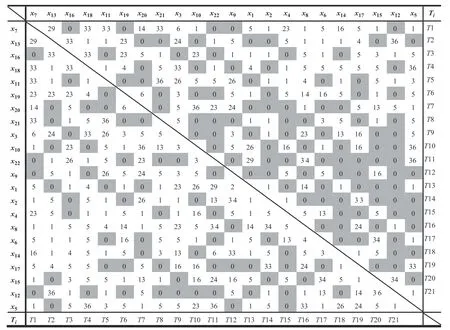
图3 TE 过程的稀疏D-vine 和D-vine 的结构信息矩阵Fig.3 Structure information matrix of sparse D-vine and D-vine for TE process

由图3 可知，稀疏D-vine 结构中独立二元Copula数量为101 个，明显高于D-vine 中的61 个，尤其在高层次树中，独立Copula 的比例增加更明显。这意味着稀疏D-vine 中需优化的二元Copula 个数比Dvine 中少40 个，而且主要集中在高层次树中，可有效减少高层次树中的累积误差，提高模型性能。

表1 示出了针对TE 过程D-vine 和SDVC 方法的离线建模和在线监测过程的CPU 耗时（CPU 2.2 GHz，RAM 8 GB）。由表1 可知，SDVC 建模计算的负担（离线建模的耗时）和实时性（在线监测）都要优于Dvine 模型。表2 示出了PCA、KPCA、D-vine 和SDVC方法在 TE 过程中的故障监测结果，粗体表示每个故障的最优检测率。

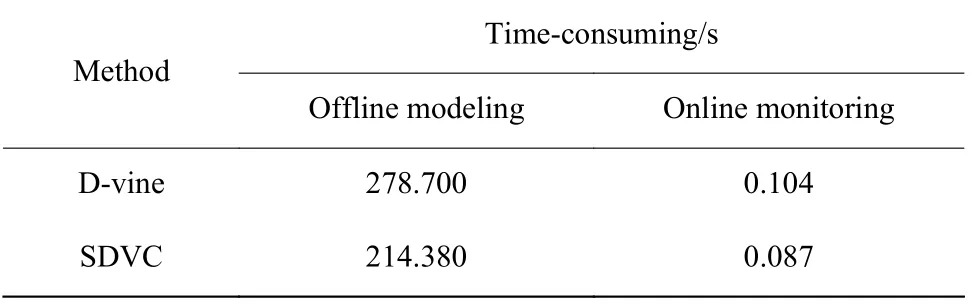
表1 D-vine 和SDVC 方法的CPU 耗时Table 1 CPU time consuming of D-vine and SDVC methods

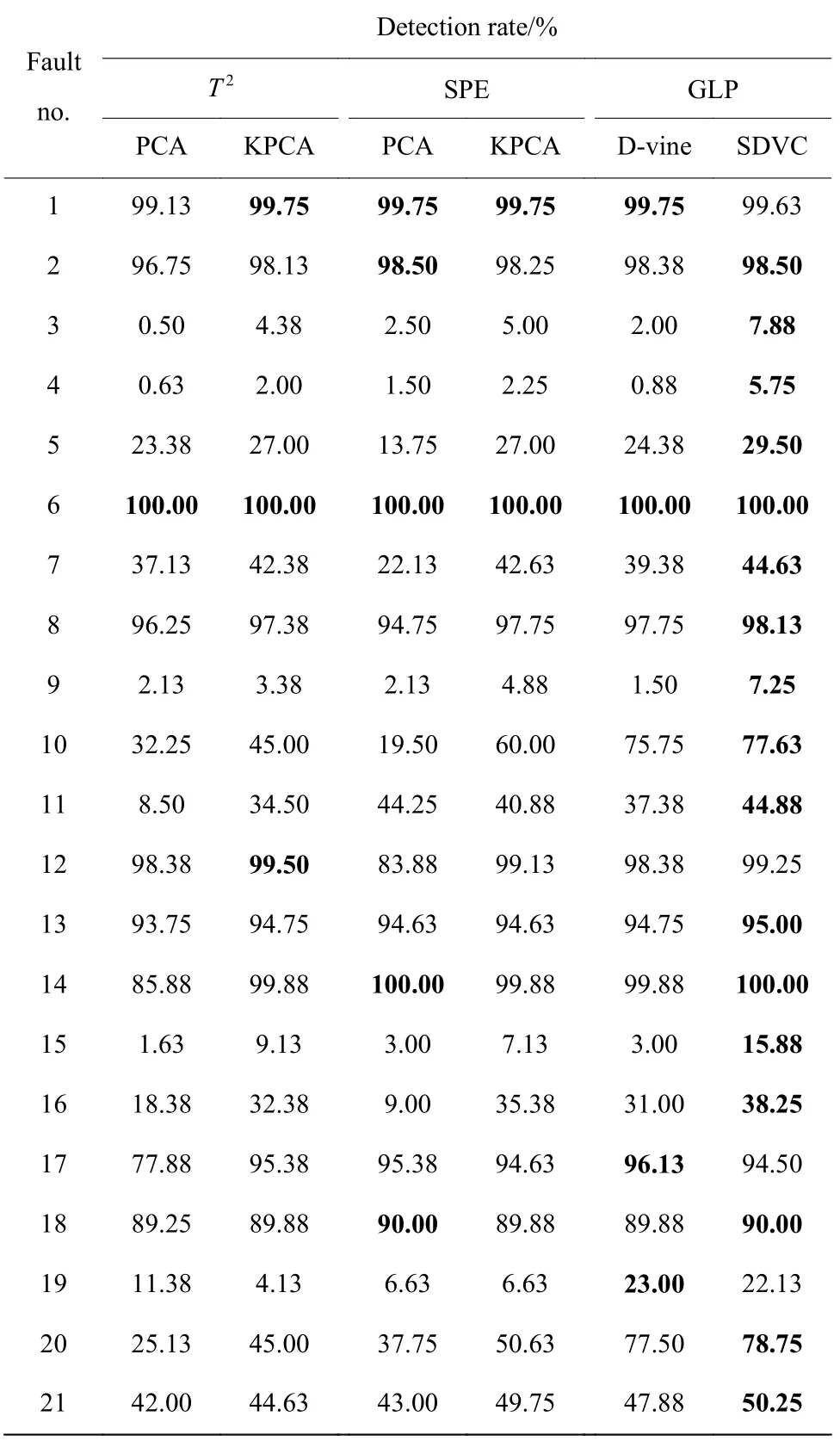
表2 TE 过程21 个故障的检测率(CL=0.99)Table 2 Fault detection rates for 21 faults of TE process(CL=0.99)

表2 结果显示，在PCA、KPCA、D-Vine 和SDVC4 种方法中，总体上本文提出的SDVC 模型监测性能最好，对于绝大多数故障类型都能够取得最好的检测效果。对于故障1、12、17 和19，SDVC 方法虽未能取得最佳检测结果，但是相应的故障检测率差别不大。对于故障3、4、5、9 和15，故障信息不容易被捕捉到，所以4 种方法都无法达到较好的效果，不过，相比较而言，SDVC 模型的检测效果要优于其他3 种方法。而对于故障2、6、8 等较易检测的故障，SDVC模型性能也优于其他3 种方法，这表明对于较易检测的故障，SDVC 依然取得好的检测效果。为更直观地展现4 种方法监测效果的不同之处，4 种方法对TE过程中故障13 的监测结果如图4 所示。

TE 过程具有高度的非线性和非高斯态，其过程数据必然具备非线性和非高斯性。PCA 在建模时默认过程数据线性相关且服从高斯分布，无法有效处理非线性非高斯问题。KPCA 擅长处理数据间的非线性信息，但难以捕捉非高斯信息，甚至可能会被作为噪声排除掉。而且这两种方法的建模过程采用了降维思想，难免会造成部分原始数据信息的丢失。D-vine 方法从相关性建模角度出发建立相关性树结构，可以较好地描述数据间的非线性和非高斯信息。然而，由于Vine Copula 建模过程的特殊性，误差容易在树结构种类中累积，导致高层次树部分结构模型不可靠。采用mBIC 优化准则对高层次树结构进行了适当的稀疏，有效地解决了这个问题，显著提高了模型的整体性能。

3.2 醋酸脱水过程

精对苯二甲酸(PTA)是工业生产聚酯、工程聚酯塑料、增塑剂等的重要原料。PTA 是以对二甲苯为生产原料，经过液相氧化生成的粗对二甲苯酸间接得到的。在液相氧化过程中，醋酸是重要的溶剂。通常，获得纯度较高的醋酸需要有效地完成醋酸脱水过程。由于普通精馏分离经常无法满足醋酸纯度要求，因此工业中采用共沸精馏法完成醋酸和水的分离[27]。经过共沸精馏分离操作后，正常状态下反应器顶部混合物中的醋酸含量一般低于1.15%。

共沸精馏法的醋酸脱水工业过程反应塔中包含90 级塔板和4 个进料口，整个系统还包括产生乙酸和水的混合物的氧化反应器等，采用包括温度、压力、流量和电导率等21 个过程变量建立模型对醋酸脱水精馏过程状态进行实时监控。离线建模阶段采用500 组正常的数据训练模型，在线监控阶段采用300 组测试数据模拟仿真，其中前100 组为正常运行状态，从101 组开始反应器顶部的醋酸质量分数上升到1.5%，并维持至第200 组，最后100 组数据的醋酸质量分数又回到1.15%以下。

表3 示出了当控制限CL=0.98、SDVC 模型中伯努利分布参数 ψ0=0.9、主成分方差贡献率为85%时，PCA、KPCA、D-vine 和SDVC 4 种方法的故障检测率(Fault Detection Rate, FDR)和误报率(False Alarm Rate, FAR)，对应的醋酸脱水过程监测图如图5 所示。由表3 可得，4 种方法都能有效地监测出异常的发生，但相对来说，SDVC 方法有着更低的误报率。这表明本文提出的SDVC 过程监测方法在醋酸脱水工业过程中有着良好的应用。

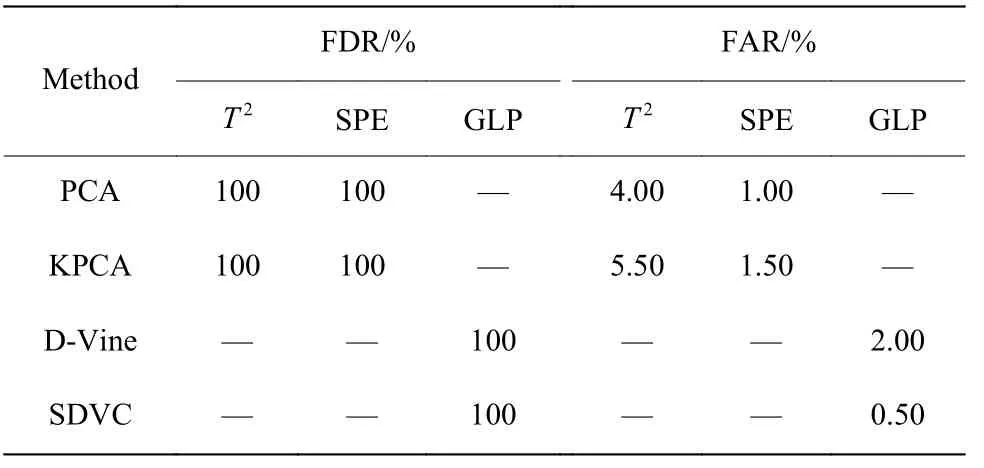
表3 醋酸脱水过程的检测率和误报率(CL=0.98)Table 3 FAR and FDR of the acetic acid dehydration process(CL=0.98)

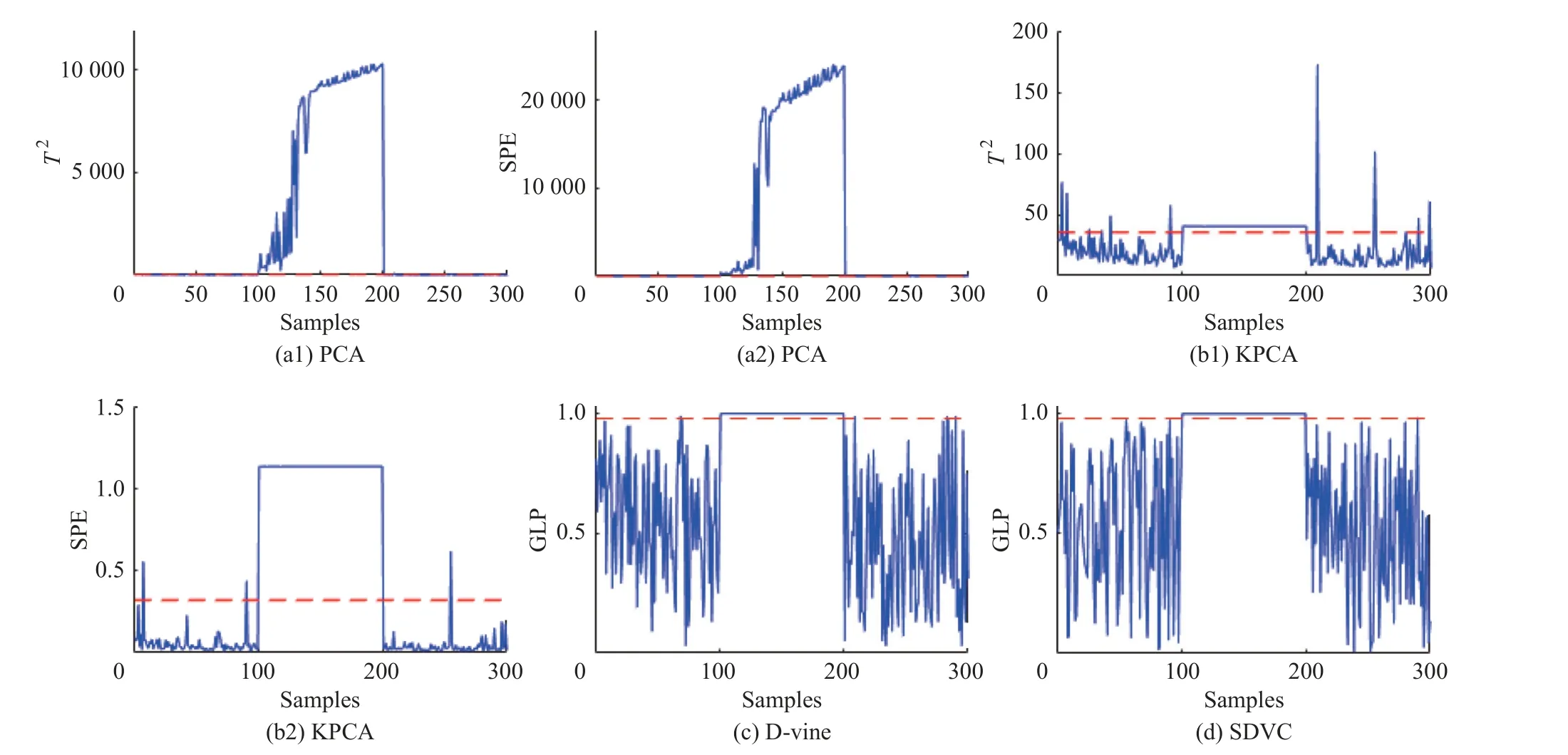
图5 醋酸脱水过程监测图Fig.5 Monitoring charts of acetic acid dehydration

4 结 论

本文提出了一种基于SDVC 模型的过程监测方法，通过两个工业实例论证了该方法在过程监测领域的优越性能。通过给不同D-vine 结构树上的二元Copula 分配符合伯努利分布的先验概率，让高层次树中的二元Copula 有更大的概率被优化为独立状态，实现了对高层次树的结构稀疏，有效减少了估计误差在结构树中的累积，提高了模型的可靠性和实时性。引入HDR 与密度分位数理论构建GLP 指标实现对工业过程的实时监测。为评估SDVC 方法的故障监测性能，应用TE 以及醋酸脱水过程作为实例进行测试实验，通过与PCA、KPCA 和D-vine 方法比较，验证了SDVC 监测模型具备良好的监测性能。