带攻角平头弹侵彻不同厚度芳纶层合板的数值模拟*

季海波，王 昕，赵振宇，赵中南，李 雪，韩佳彤，卢天健

（1.南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016；2.南京航空航天大学多功能轻量化材料与结构工信部重点实验室，江苏 南京 210016；3.西安交通大学机械结构强度与振动国家重点实验室，陕西 西安 710049；4.新加坡国立大学冲击动力学实验室，新加坡 117575；5.西北核技术研究院，陕西 西安 710024）

水面舰船是海战中的重要作战平台，主要威胁来自反舰导弹的打击[1]。反舰导弹战斗部爆炸时通常产生多种毁伤元，其中，高速破片群对舰船生命力的威胁最大[2]，其具有数量多、随机性大、穿透力极强的特点，可能对弹药舱、燃油舱等重要部位造成打击，且极易发生火灾弹药殉爆等次生灾害，从而导致船沉人亡的严重后果[3]。随着反舰导弹战斗部技术的发展，其爆炸产生的破片侵彻能力更强，对舰船防护结构的抗侵彻性能提出了更高要求[4]。增加舰艇金属舱壁的厚度可进一步提升其抗侵彻性能，但也会大幅增加舰船的重量，影响其作战的机动性能，故纤维增强复合材料逐渐被引入舰船防护领域[5]。其中，以玻璃纤维增强复合材料（glass fiber reinforced plastic, GFRP）、芳纶纤维复合材料（aramid fiber reinforced plastic, AFRP）和超高分子量聚乙烯纤维复合材料（ultra-high molecular weight polyethylene fiber reinforced plastic, UFRP）的应用最为广泛：GFRP 的价格低廉、阻燃性能好、结构性能优良，但比防护性能最低；UFRP 的比防护性能最高，但纤维的阻燃性较差、熔点较低，不适用于对阻燃性能要求较高的重点防护领域（如舰船）；AFRP 的比防护性能介于GFRP 与UFRP 之间，同时具备高比强度、高比刚度以及阻燃的优异性能，在舰船乘员舱、弹药舱、燃烧室等重点防护领域具有明显优势[5]。

子弹（破片）冲击作用下，芳纶层合板的防护机理主要包括：纤维拉伸、基体开裂、层合板分层、弯曲、剪切冲塞及层合板运动等[6-7]。进一步的研究发现，基体种类对芳纶层合板的弹道性能有重要影响：相同面密度条件下，热塑性基体芳纶层合板的抗弹性能明显优于热固性基体芳纶层合板[8-10]，后者主要依靠整体刚性吸收部分能量，前者则依靠纤维的剪切破坏、分层及变形吸收大量能量[8]；采用环氧树脂改性的酚醛树脂作为基体制备芳纶层合板，可明显提高其粘结强度，且当其环氧树脂含量保持在6%时，防弹性能达到最优[11]。此外，芳纶层合板的变形和破坏机理与靶板厚度有关：薄板主要发生纤维断裂，而厚板在侵彻后的分层现象更为明显[12]；通过扫描电镜观察子弹侵彻厚芳纶层合板后的断面，发现不同层表现出不同的破坏机制，前层主要发生剪切破坏而后层主要发生纤维拉伸破坏[13]。关于子弹形貌的研究表明[14-15]：尖头弹的侵彻性能优于平头弹；锥形弹丸冲击下，芳纶的主要失效机制为纤维断裂，变形与损伤范围较为局部；平头弹丸冲击下，除了纤维断裂，芳纶还产生更大范围的分层。针对弹丸速度的研究结果表明，入射速度低于弹道极限时，芳纶层合板的分层区域面积随入射速度增大而增大；入射速度高于弹道极限时，分层区域面积随入射速度增大而减小；靶板的能量吸收率随子弹速度的增加而减小[7]。

上述研究大多考虑弹丸以零着角垂直入射芳纶层合板的理想状况。实际应用中，由于爆炸产生破片具有随机性，弹体往往以带着角与攻角的非理想侵彻状态入射目标[16]，如图1(a)所示：着角定义为弹体速度与靶板法线的夹角，攻角定义为弹体轴线与弹体速度的夹角。国内外针对弹丸带着角侵彻芳纶层合板的研究较少：张明[17]通过数值模拟方法，获得了着角对Kevlar 129/乙烯-乙酸乙烯酯复合材料半无限靶板弹道特性的规律，发现随着着角增大，破片侵彻靶板的有效深度加速减小，侵彻入口毁伤面积增大，应力分布也越来越不均匀。针对弹丸带攻角侵彻芳纶层合板这个问题（图1(b)），尚未见公开报道。

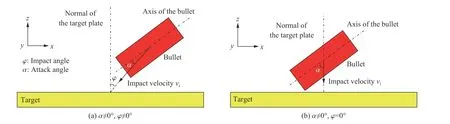
图1 子弹侵彻靶板的着角φ 与攻角α 示意图Fig.1 Schematic of impact angle φ and attack angle α of flat-nosed projectile impacting a target plate

综上，针对弹丸带攻角侵彻复合材料层合板的相关研究尚比较缺乏。现有文献针对弹丸带攻角侵彻金属和混凝土研究结果表明：攻角会显著影响子弹的剩余速度[18-20]、变形毁伤[21]、轨迹偏转[22-26]、靶板的毁伤[26-28]等，在工程应用中不可忽视。本文中，以广泛应用于舰船防护领域的芳纶层合板为研究对象，在弹丸的着角为零但攻角不为零的情况下（图1(b)），采用有限元模拟方法，系统探究平头弹侵彻不同厚度芳纶层合板的弹道响应。重点研究3 个关键科学问题：(1)攻角对芳纶层合板抗侵彻性能的影响规律；(2)攻角与芳纶层合板厚度和弹丸入射速度的联系；(3)攻角影响芳纶层合板抗侵彻性能的力学机理。

1 有限元模型

芳纶层合板的数值分析通常采用两种方法进行建模：一种是细观建模方法[14,29]，将纤维束与基体分开建模，这样可很好地模拟纤维与基体的特性，但不易把握层合板中纤维与基体的相互作用对其整体性能的影响，计算成本较高；另一种是宏观建模方法[6,12-13,30]，不考虑层合板的内部结构，宏观上把一层或若干层等效为均匀的正交各向异性材料。宏观建模方法简单实用，计算效率高，适合工程实践，故本文采用宏观建模。

1.1 模型描述

采用商用软件LS-DYNA R7.0.0 进行数值模拟，三维有限元模型，如图2 所示。该模型关于xOz平面对称，子弹速度沿−z方向垂直于靶板平面，子弹攻角用其轴线与速度的夹角α 表示，取值范围为0°～30°[27]。

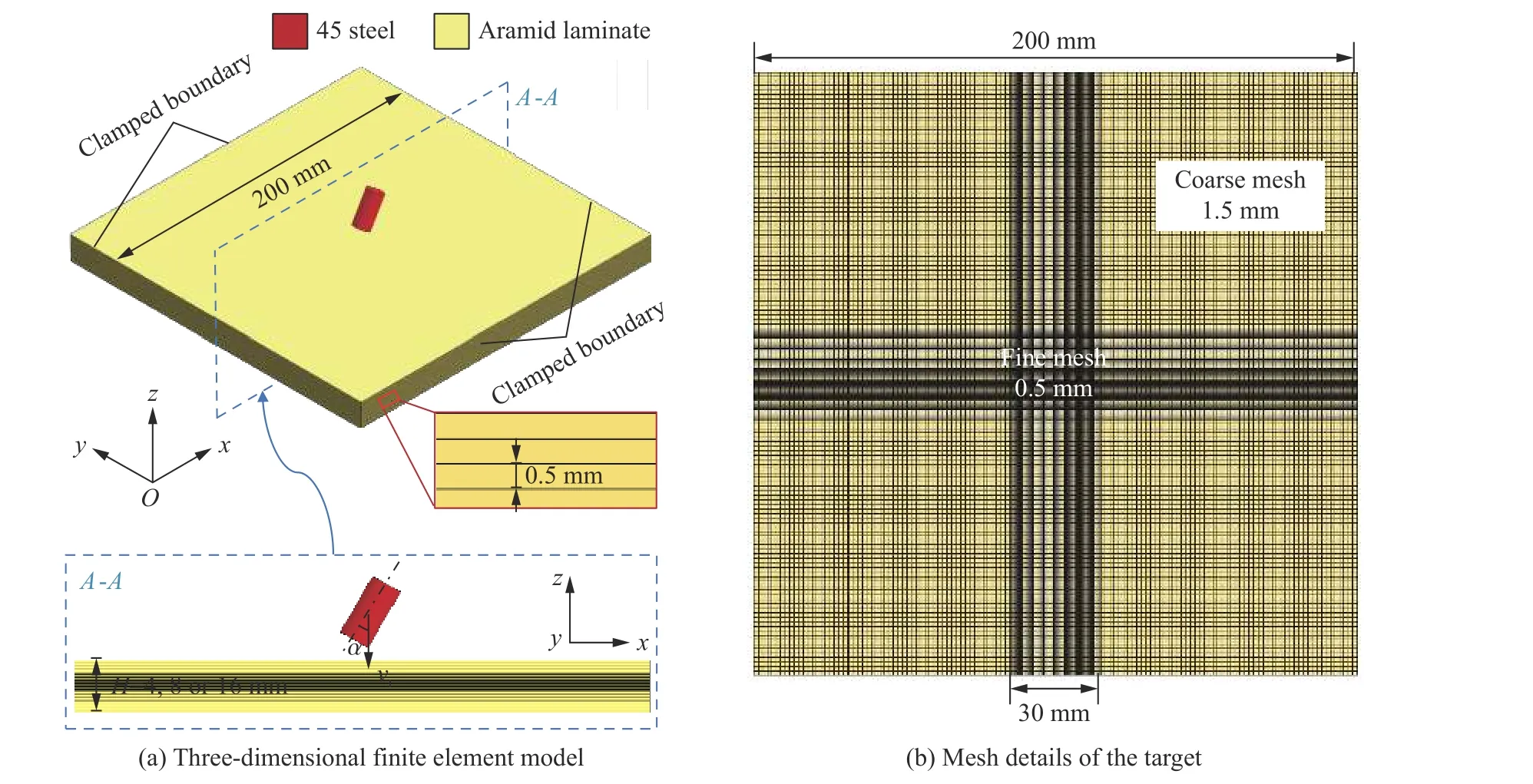
图2 带攻角侵彻芳纶层合板的数值模型Fig.2 Simulation model of impacting aramid laminate with attack angle

计算模型包括圆柱形平头弹与正方形靶板两部分，几何尺寸与边界条件如图2 所示：靶板边长200 mm，厚度设置薄（4 mm）、中厚（8 mm）、厚（16 mm）等3 种规格[31-32]；子弹直径10 mm、长度20 mm；模型四周固支。其中，靶板为芳纶层合板，由Kevlar29 平纹织物与环氧树脂真空灌注法制备而成[12]；制备时，将若干层织物堆叠后灌注环氧树脂，渗透约15 min，真空常温下固化24 h，再常压60℃下固化12 h 成型。所用纤维直径约为0.54 mm，编织出的平纹织物面密度为440 g/m2，织物密度为每10 cm 长度内67 根纱线。芳纶层合板的纤维体积分数约为60 %，其单层厚度约为0.5 mm，与实际厚度近似相等。子弹母材为广泛采用的45 钢[19,33]。

采用八节点六面体实体单元SOLID 164 对子弹与靶板进行网格划分：子弹的平均网格尺寸为0.25 mm[34-35]；靶板沿厚度方向的网格尺寸为0.5 mm，在中心30 mm（子弹直径的3 倍）边长的正方形区域内，面内网格尺寸为0.5 mm，外缘区域的面内网格尺寸则为1.5 mm[36]。针对靶板网格尺寸无关性的分析在后文中给出。为防止网格发生沙漏变形，采用Flanagan-Belytschko 刚度形式进行沙漏控制。弹丸与层合板之间的接触定义为面-面侵蚀接触，采用基于segment 的接触算法，以时间步长计算接触刚度，防止因刚度或网格差异造成的穿透现象[37]。本文中模型忽略子弹与靶板之间的摩擦[6,38]。

1.2 材料模型

1.2.1 芳纶层合板

采用MAT_ENHANCED_COMPOSITE_DAMAGE 本构模拟均匀化单层芳纶板的力学行为，该材料模型已成功地用于研究纤维增强复合材料的抗冲击问题[6,12,14,39]。单层板发生失效前，假设其保持正交各向异性弹性，应力和应变之间的关系式为：

式中：E、G、ν分别代表均匀化层合板的杨氏模量、剪切模量和泊松比。

根据Chang-Chang 失效准则[37]刻画芳纶单层板的失效破坏，包括纵向拉伸失效、纵向压缩失效、横向拉伸失效和横向压缩失效。

纵向拉伸失效：

纵向压缩失效：

横向拉伸失效：

横向压缩失效：

式中：Xt为纵向拉伸强度，Xc为纵向压缩强度，Yt为横向拉伸强度，Yc为横向压缩强度，Sc为面内剪切强度。β 表示纵向拉伸失效模式中剪切项的权重系数，取值为0[37]。＞ 0（i= f, c, m, d）时，材料失效。相邻芳纶单层板之间通过粘接接触（AUTOMATIC_SURFACE_TO_SURFACE）进行连接，判定其界面是否失效的准则为[37]：

式中：σn和 τ 为接触节点处的法向应力和切向应力，Sn和Ss为法向与切向的破坏阈值应力。界面发生失效前，接触节点被绑定；界面发生失效后，不再传递拉伸与剪切应力。

芳纶层合板的具体材料参数取自文献[12]，如表1 所示。

表1 芳纶层合板本构模型及失效准则相关材料参数[12]Table 1 Material parameters of constitutive model and failure criterion for aramid laminate[12]

1.2.2 45 钢

在冲击或爆炸等动态加载下，金属材料经历大范围的应变、应变率、温度和复杂的应力状态，其力学行为响应受到极大影响[34,40]。冲击力学常用的本构方程有Cowper-Symonds 模型[41]、Johnson-Cook 模型[42]、Zerilli-Armstrong 模型[43]和Steinberg-Guinan 模型[44]等。其中，针对Johnson-Cook 模型的研究较广，且在舰船抗爆抗冲击领域有广泛的应用。

采用考虑金属材料应变硬化、应变率及温度效应的Johnson-Cook 模型作为45 钢的本构方程：

式中：A、B、n、C和m为模型常数，σeq为等效塑性应力，εpl和 ε ˙pl分别为等效塑性应变和应变率，ε ˙0为参考应变率，Tr为室温，Tm为熔化温度。

进一步采用Johnson-Cook 断裂准则表征45 钢的韧性断裂，该准则考虑了应力三轴度、应变速率和温度对断裂应变的影响，定义材料单元的损伤参数为：

式中：∆ εpl为单个计算步内等效塑性应变的增量，εf为材料断裂时的等效塑性应变。D= 1 时，材料单元断裂。εf的数学表达式为：

式中：D1、D2、D3、D4和D5为模型参数；=σm/σeq为应力三轴度，σm为平均应力。

针对45 钢的塑性形变和韧性断裂，表2 给出了本文中采用的相关材料模型参数[45]。

表2 45 钢塑性变形及韧性断裂模型的相关材料参数[45]Table 2 Material parameters of plastic deformation and ductile fracture models for 45 steel[45]

1.3 网格无关性与能量守恒分析

为得到最优的网格尺寸，以速度为300 m/s 的平头弹理想入射4 mm 芳纶层合板这一工况为例，对有限元模型进行网格无关性分析。图3 给出了子弹剩余速度随着芳纶面内与面外网格尺寸的变化趋势：面内尺寸从2.0 mm 逐步减小至0.75 mm 时，子弹剩余速度持续增加，但网格尺寸进一步从0.75 mm 减小到0.25 mm 时，子弹剩余速度趋于稳定；面外尺寸从0.5 mm 逐步减小到0.125 mm 时，子弹剩余速度基本不变。基于上述结果，本文中选择的面内尺寸与面外尺寸均为0.5 mm，单元尺寸比例较均衡。

图3 网格无关性分析Fig.3 Mesh-independent analysis

为验证有限元模拟的可靠性，需检验计算过程中的能量守恒[46-47]。图4 显示选取最优网格尺寸时，数值模拟得到的能量时程曲线。结果表明，在撞击后的任何时刻，动能、内能、沙漏能和滑移能之和等于整个系统的总能量，且总能量几乎恒定。沙漏能量远小于总能量的10 %，滑动能量远小于内能的10 %。总体而言，本文中数值模拟达到了较好的能量平衡。

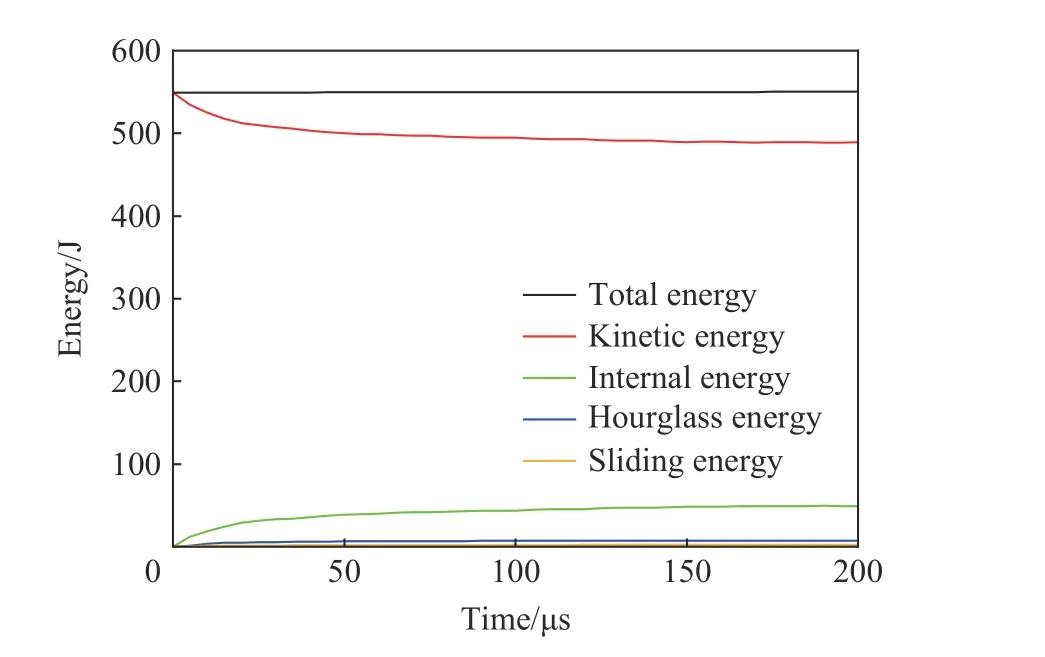
图4 有限元模拟的能量历程Fig.4 Energy histories by finite element simulations

2 有限元模型验证

为验证芳纶纤维增强复合材料模型的有效性，针对已开展的弹道冲击实验[12]进行数值分析：该实验采用0.357 马格南子弹，以理想状态侵彻不同层数的环氧基Kevlar29 纤维增强复合材料靶板。子弹由铅芯与黄铜外壳组成，直径9 mm，总质量10.2 g。靶板边长160 mm，每层厚度0.5 mm，层数分别为8、13、18 和28 层。验证模型如图5 所示，其设置与文献[12]描述完全相同。子弹网格尺寸为0.25 mm，靶板网格尺寸为0.5 mm。由于整个模型对称，只建立1/4 模型，在靶板的边界和对称面节点上分别施加固定约束条件和对称约束条件。子弹中的铅和铜采用LS-DYNA 内置的MAT_JOHNSON_COOK 材料模型模拟，具体参数见表3，其中，Wcr为材料开始失效时其单位体积的塑性功。

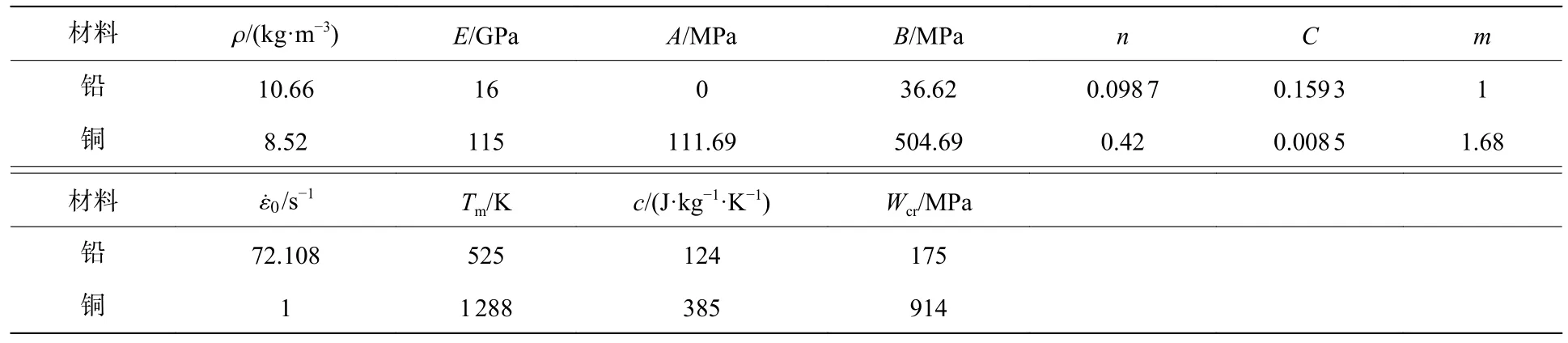
表3 铅和铜的塑性形变及断裂模型相关材料参数[45]Table 3 Material parameters of plastic deformation and ductile fracture models for lead and copper[45]

图5 马格南子弹侵彻芳纶层合板数值模型Fig.5 The numerical model for a magnum projectile penetrating aramid laminates

速度为440.51 m/s 的0.357 马格南子弹冲击八层芳纶层合板，图6 比较了其经过数值模拟和实验得到的失效模式。随着入射深度的增大，该芳纶层合板的穿孔孔径与变形区域不断变大，孔洞附近呈现锥形的背部突起，在厚度方向上发生膨胀且有明显的分层现象，计算得到的层合板损伤模式与实验观察基本吻合。表4 和图7 给出的结果进一步表明，对于不同层数的芳纶层合板，数值模拟得到的子弹剩余速度与实验结果之间的相对误差在10 %以内。上述结果证明了本文中数值模型的可行性和有效性。

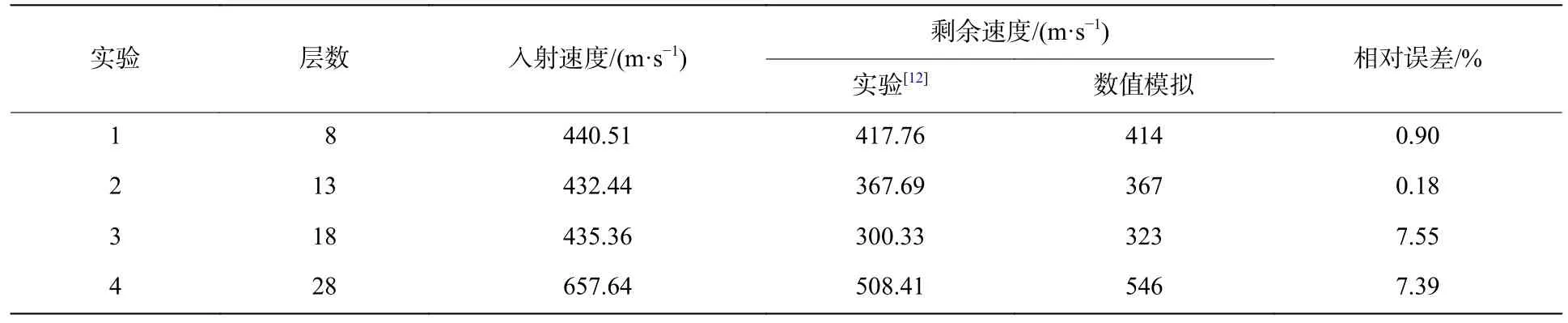
表4 数值模拟和实验结果对比Table 4 Comparison between numerically calculated results and experimentally results

图6 速度为400.51 m/s 的马格南子弹冲击八层芳纶层合板数值模拟与实验[12]得到的失效模式对比Fig.6 Comparison between simulated and experimental[12]failure modes of the eight-layer aramid laminate impacted by the magnum projectile at 400.51 m/s

图7 马格南子弹冲击具有不同层数的芳纶层合板数值模拟和实验剩余速度的对比Fig.7 Comparison between simulated and experimental residual velocities of the magnum projectile penetrating aramid laminates with different layers

3 数值模拟结果

式中：vi为 入射速度，vr为剩余速度，vbl为 弹道极限，α和 β 为模型待标定的参数。

为表征层合板在冲击过程中吸收能量的能力，定义能量吸收率为[49]：

式中：mp为弹丸质量。本文中假设侵彻后弹丸质量不变。将式(10)代入式(11)，可得：

穿孔能阈值定义为弹道极限速度时子弹的动能：

3.1 厚度4 mm 芳纶层合板的抗侵彻性能

本节研究攻角α 为0°、10°、15°、20°和30°情况下，薄芳纶层合板（厚度4 mm）的弹道响应。图8(a)绘制了不同攻角入射该层合板的剩余弹速曲线，曲线与横轴交点的坐标值即为靶板弹道极限速度。可见，靶板弹道极限速度随攻角增大而降低，但曲线在入射速度约为250～300 m/s 区间内相交：子弹初始速度较低（vi≤250 m/s）时，其剩余速度随攻角增大而增大；高速（vi≥300 m/s）下的趋势则相反，相关机理将在下文中详细分析。

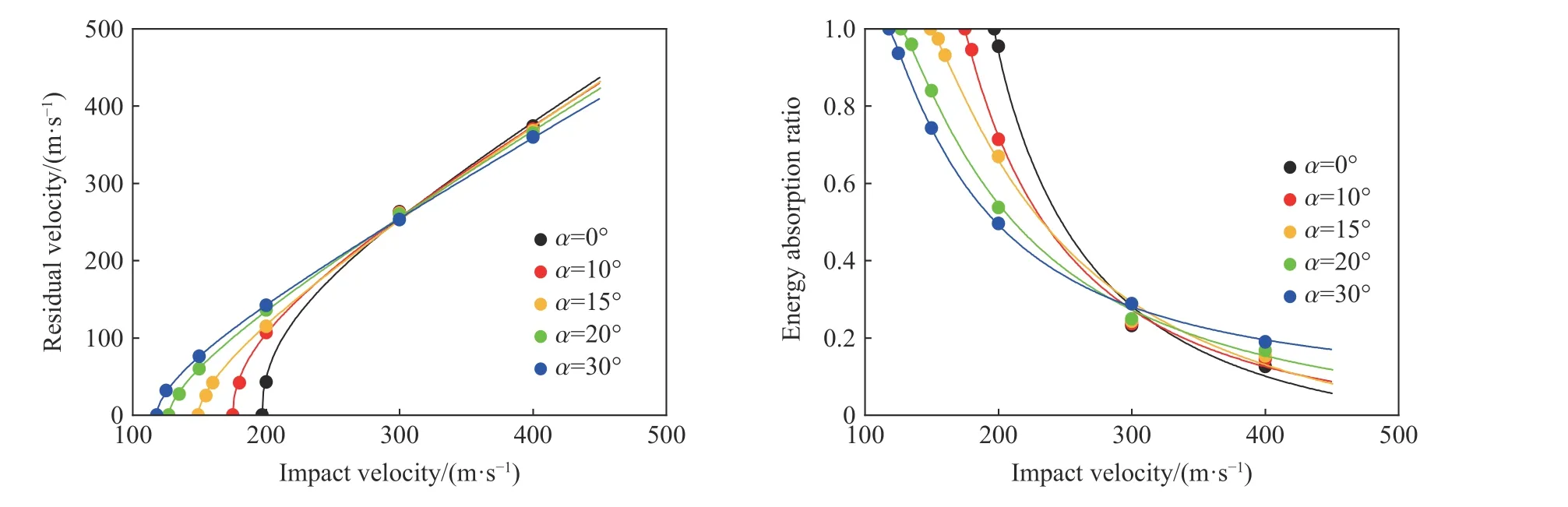
图8 攻角对4 mm 厚芳纶层合板剩余弹速和能量吸收率的影响Fig.8 Effect of attack angle on residual velocity and energy absorption ratio of 4-mm-thickness aramid laminates

靶板的能量吸收率曲线如图8(b)所示。随着入射速度提高，靶板能量吸收率不断下降，且曲线也在250～300 m/s 区间内相交。图9 定量描述了弹道极限速度和穿孔能量阈值。相较于零攻角入射，30°攻角入射情况下的靶板弹道极限速度降低了40.1%，对应的穿孔能量阈值降低了64.1%。

图9 攻角对4 mm 厚芳纶层合板弹道极限速度和穿孔能量阈值的影响Fig.9 Effect of attack angle on ballistic limit velocity and perforation energy threshold of 4-mm-thickness aramid laminates

3.2 厚度8 mm 芳纶层合板的抗侵彻性能

攻角α 为0°、10°、15°、20°和30°下，图10～11 给出了采用有限元模型得到的中厚芳纶层合板（厚度8 mm）的弹道响应。与薄板类似，子弹的初始速度较低时，攻角有利于其侵彻靶板，在高速下则相反。与薄板不同的是，攻角导致靶板弹道极限速度和穿孔能量阈值降低的幅度更小：相较于零攻角入射，30°攻角入射下，8 mm 芳纶层合板的弹道极限速度降低了16.8%，穿孔能量阈值降低了30.6%。

图10 攻角对8 mm 厚芳纶层合板剩余弹速和能量吸收率的影响Fig.10 Effect of attack angle on residual velocity and energy absorption ratio of 8-mm-thickness aramid laminates

图11 攻角对8 mm 厚芳纶层合板弹道极限速度和穿孔能量阈值的影响Fig.11 Effect of attack angle on ballistic limit velocity and perforation energy threshold of 8-mm-thickness aramid laminates

3.3 16 mm 厚度芳纶层合板的抗侵彻性能

攻角α 为0°、10°、15°、20°和30°情况下，厚芳纶层合板（16 mm）的弹道响应如图12～13 所示。基本规律与薄板和中厚板类似，但攻角对靶板弹道极限速度与穿孔能量阈值降低的幅度进一步减小：相比于零攻角入射，30°攻角入射情况下，16 mm 厚芳纶层合板弹道极限速度仅降低5.5%，对应的穿孔能量阈值降低10.6%。

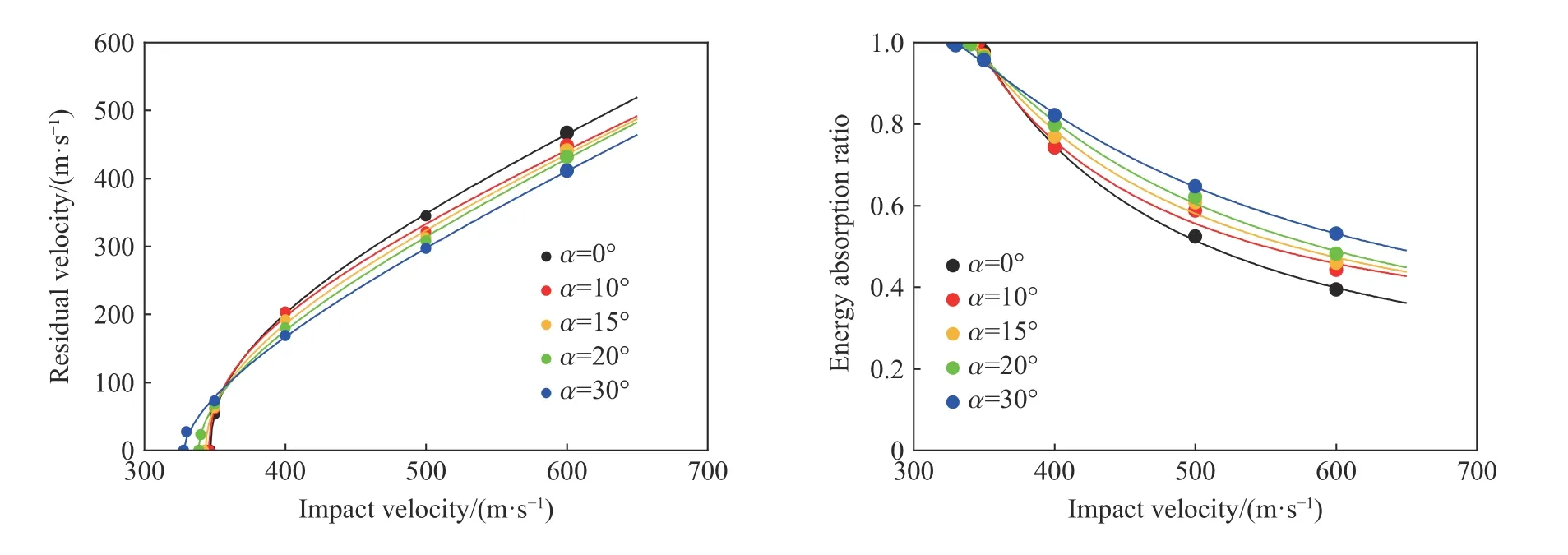
图12 攻角对16 mm 厚芳纶层合板剩余弹速和能量吸收率的影响Fig.12 Effect of attack angle on residual velocity and energy absorption ratio of 16-mm-thickness aramid laminates

图13 攻角对16 mm 厚芳纶层合板弹道极限速度和穿孔能量阈值的影响Fig.13 Effect of attack angle on ballistic limit velocity and perforation energy threshold of 16-mm-thickness aramid laminates

4 讨 论

4.1 攻角对芳纶抗侵彻性能的影响

第3 节给出的计算结果表明，子弹攻角α 在0°～30°范围内，靶板弹道极限速度vbl与穿孔能量阈值Ear随α 的增大而单调降低。vbl与α 的关系可采用基于指数函数的公式拟合，即：

式中：v0为零攻角入射下的弹道极限速度，γ为待标定的参数，其值大小反映了攻角导致靶板极限弹速降低的程度。将式(13)代入式(14)，可得Ear与α 的关系式：

式中：E0为零攻角入射下的穿孔能量阈值。

拟合结果如图14 所示。可见，随着靶板厚度的增大，v0与E0均增大，满足一般物理规律；预测对应γ也增大，表明攻角导致弹道极限速度与穿孔能量阈值降低的程度随靶板厚度增大而减小。

图14 攻角对芳纶层合板弹道极限速度和穿孔能量阈值的影响Fig.14 Effect of attack angle on ballistic limit velocity and perforation energy threshold of aramid laminates

4.2 不同弹速下攻角对芳纶层合板抗侵彻性能的影响机理

上文中的结果表明，薄、中厚及厚芳纶层合板均呈现低速下攻角有利于侵彻，高速下攻角不利于侵彻的规律。本小节以4 mm 芳纶层合板（薄）为例，对不同弹速下攻角影响侵彻性能的机理进行分析。子弹以200 m/s 零攻角侵彻该层合板，图15(a) 显示其x方向应力云图。20 µs 时，芳纶板开始发生局部弯曲，材料尚未发生损伤；55 µs 时，还未发生损伤的芳纶层（厚3 mm）产生膜拉伸变形以耗散弹丸动能，而已发生损伤的单层内部的应力值很小；140 µs 时，子弹尚未穿透靶板，其背突直径为106.5 mm。该芳纶层合板的防弹机理主要是通过一定范围内材料的整体弯曲和膜拉伸变形耗散子弹动能，这与超高分子量聚乙烯薄板侵彻实验[50]中观察到的破坏模式类似。

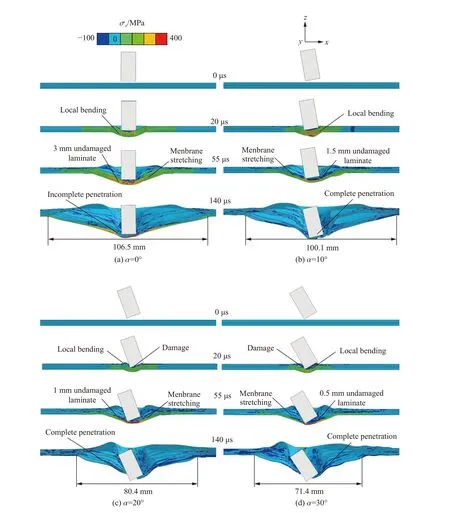
图15 入射速度200 m/s 下不同攻角侵彻4 mm 厚芳纶层合板的x 方向应力分布Fig.15 Distribution of x-directional stress in 4-mm-thickness aramid laminates penetrated by the flat-nosed projectile with a fixed impact velocity of 200 m/s and varying attack angles

随着子弹攻角的增大，子弹与芳纶层合板初始接触面积变小，局部应力集中使得芳纶层合板更易满足失效准则进而发生断裂，如图15(b)～(d)所示，进而导致同一时刻芳纶层合板参与膜拉伸的层数更少：55 µs 时，10°、20°和30°攻角下，未损伤的厚度分别减少到1.5、1.0 和0.5 mm，且每一层参与膜拉伸的范围更小：在140 µs 时，3 种攻角下，靶板背突直径分别减少到100.1、80.4 和71.4 mm。可见，增加攻角在一定程度上抑制了芳纶层合板产生大面积的膜拉伸，导致其弹道极限速度大幅降低。

另一方面，子弹以300 m/s 的速度零攻角入射芳纶层合板时，图16(a)给出了其x方向的应力云图：相较于图15(a)，高速情况下侵彻所用时间明显更短。30 µs 时，芳纶层合板中的横波尚未传播到较远处，靶板已在厚度方向上被贯穿；70 µs 时，芳纶层合板被子弹完全穿透，因而此后几乎不再影响子弹速度，其背突直径减小到46.3 mm（相比于低速下的106.5 mm）。此时，靶板受冲击影响的区域更小，发生弯曲与参与膜拉伸的材料更少。随着子弹攻角的增大，靶板的破坏模式未发生显著改变，但带攻角的子弹侧面与靶板接触，增加了其侵彻阻力，如图16(b)～(d)所示。

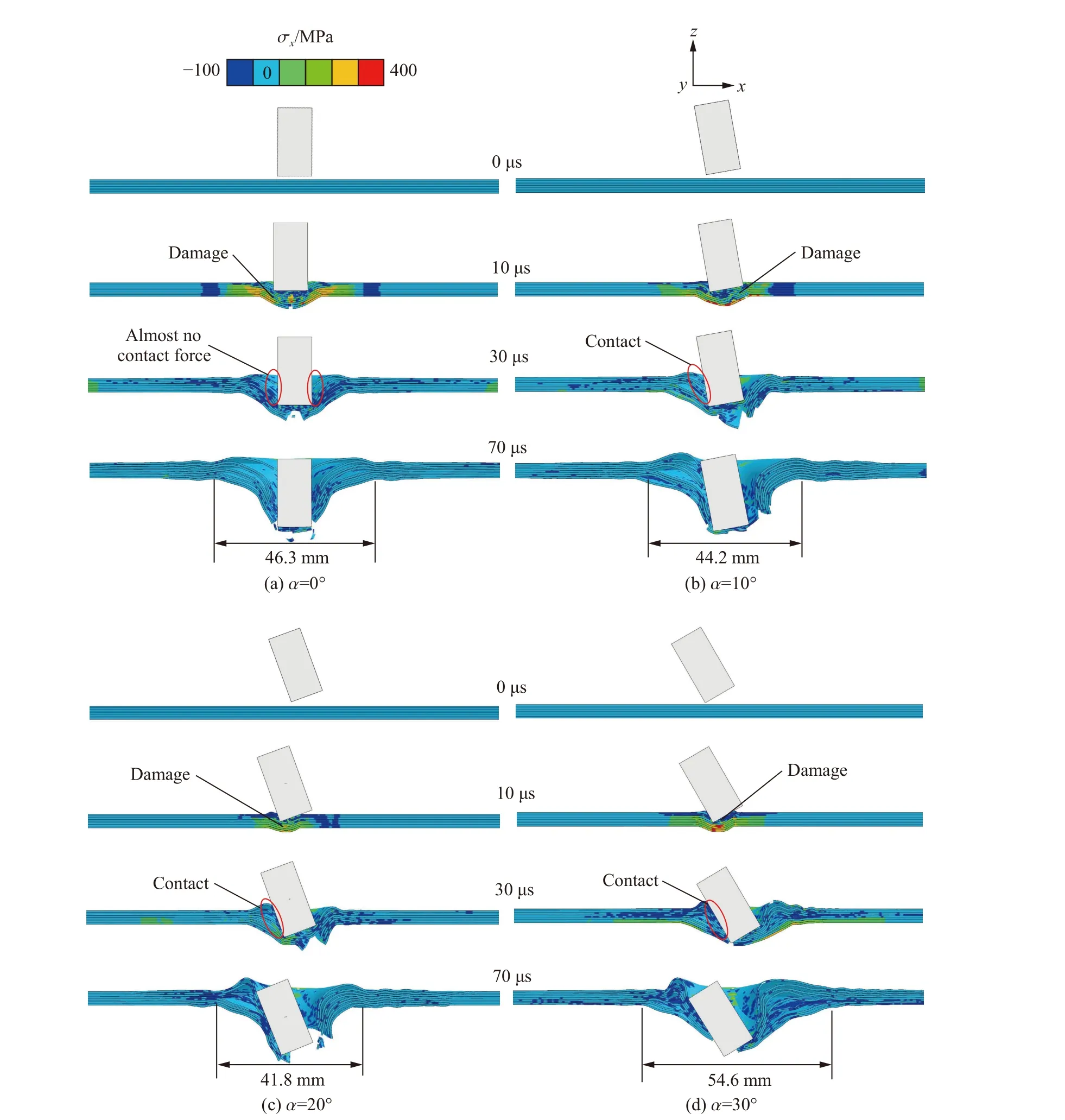
图16 入射速度300 m/s 下不同攻角侵彻4 mm 厚芳纶层合板的x 方向应力分布Fig.16 Distribution of the x-directional stress in 4-mm-thickness aramid laminates penetrated by the flat-nosed projectile with the fixed impact velocity of 300 m/s and varying attack angles

在2 种不同入射速度下，图17 给出了子弹与靶板接触力随时间变化的曲线。vi=200 m/s 时，子弹以零攻角入射的接触力始终大于带攻角入射的接触力，靶板对子弹的冲量随攻角增大而降低，因而此时带攻角侵彻更危险；vi=300 m/s 时，完全穿孔后（＞30 µs）的靶板与零攻角侵彻子弹的接触力明显小于其他攻角情况，导致靶板对子弹的冲量随攻角增大而增加，因而此时零攻角侵彻反而更危险。

图17 不同攻角侵彻4 mm 厚芳纶层合板接触力-时间曲线Fig.17 Contact force-time curves of 4-mm-thickness aramid laminates penetrated with different attack angles

4.3 不同厚度下攻角对芳纶层合板侵彻性能的影响机理

4.1 节给出的结果表明，攻角导致靶板弹道极限速度降低的幅度随靶板厚度增大而减小。vi=250 m/s时，图18 给出了8 mm 厚靶板的x方向应力云图。子弹以零攻角入射时，芳纶层合板的破坏模式为渐进失效[49]，其背部材料的膜拉伸是子弹动能耗散的原因。α=30°时，应力集中导致参与膜拉伸的材料减少，这与4 mm 厚薄板类似；但是，已发生断裂的芳纶层合板与子弹侧面接触，不仅直接提升了子弹侵彻阻力，还在一定程度上使未损伤层的应力集中得到缓解，这又与薄板有所不同。攻角对16 mm 厚板的影响机理与8 mm 中厚板类似，如图19 所示。

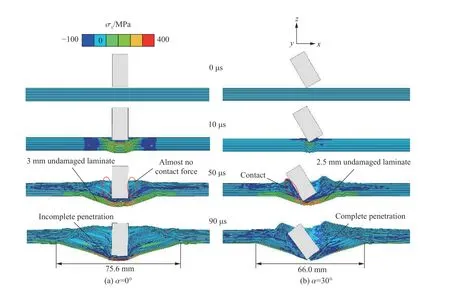
图18 入射速度250 m/s 下不同攻角侵彻8 mm 厚芳纶层合板的x 方向应力分布Fig.18 Distribution of the x-directional stress in 8-mm-thickness aramid laminates penetrated by the flat-nosed projectile with the fixed impact velocity of 250 m/s and varying attack angles

图19 入射速度350 m/s 下不同攻角侵彻16 mm 厚芳纶层合板的x 方向应力分布Fig.19 Distribution of the x-directional stress in 8-mm-thickness aramid laminates penetrated by the flat-nosed projectile with the fixed impact velocity of 350 m/s and varying attack angles

图20 给出了8 和16 mm 靶板与子弹接触力随时间的变化曲线。相比于图17(a)，在侵彻前期，零攻角入射及30°攻角入射2 种情况下接触力峰值之间的差距随靶板厚度的增加而降低；在侵彻后期，30°攻角入射下的接触力反超零攻角入射下的接触力。随着靶板厚度的增加，靶板对子弹的冲量在零攻角与30°攻角2 种情况下的差距不断减少，攻角导致靶板极限抗弹性能降低的程度也不断减弱。

图20 子弹以不同攻角侵彻8 和16 mm 厚芳纶层合板的接触力-时间曲线Fig.20 Contact force-time curves for penetration of 8 and 16-mm-thickness aramid laminates by a projectile with varying attack angles

5 结 论

针对平头弹以不同攻角侵彻芳纶层合板，本文中采用有限元建立了三维数值模型，首先通过与现有实验结果的对比，验证了所采用本构模型及数值模拟的可靠性，然后基于该数值模型，对芳纶层合板在0°～30°攻角范围内的抗平头弹侵彻响应进行了数值模拟，得到了薄（4 mm）、中厚（8 mm）和厚（16 mm）3 种规格芳纶层合板的弹道响应，包括子弹剩余速度、靶板能量吸收率、极限弹道速度与穿孔能量阈值。在所研究的工况范围内，主要结论如下。

(1) 3 种规格芳纶层合板的弹道极限速度和穿孔能量阈值均随攻角的增大而降低；弹道极限速度和穿孔能量阈值与攻角的关系可通过指数函数模型拟合。

(2)攻角对芳纶层合板抗侵彻能力的影响与其厚度有关，攻角导致靶板极限弹道速度与能量吸收阈值降低的幅度随靶板厚度的增大而降低。

(3)攻角的影响与子弹入射速度有关，入射速度接近靶板弹道极限时，剩余速度随攻角增大而增大，入射速度远大于弹道极限时，结论相反。

(4)攻角的引入一方面使芳纶层合板局部更容易发生强度失效，从而抑制了其大范围的膜拉伸，有利于子弹侵彻；另一方面增大了子弹与靶板的接触面积，侵彻阻力提升，不利于子弹侵彻。随着板厚与子弹入射速度的降低，前者占据主导作用，反之，后者主导。