爆炸冲击波与破片联合作用下防弹衣复合结构防护效果的数值模拟*

王 智，常利军，黄星源，蔡志华

（湖南科技大学机械设备健康维护湖南省重点实验室，湖南 湘潭 411201）

随着恐怖事件、地区争端和局部冲突的不断增加，爆炸冲击波与破片冲击已成为人类生命财产安全的重大威胁。对近几次局部冲突的统计表明，冲击波损伤的发生率约为50%，破片损伤的发生率为53%～81%[1-2]。由于战场形式的转变，现代战争中士兵往往受到冲击波与破片的复合毁伤，冲击波与破片联合作用导致的损伤比单独作用的损伤更加严重[3-6]。因此，针对爆炸冲击波与破片联合作用下的防护研究具有重要意义。

针对单独爆炸冲击波或破片作用造成损伤的防护问题已有大量的研究。崔小杰等[7]提出了一种由胶体、聚氨酯和泡沫铝等3 种材料作防护介质，凯夫拉(Kevlar)材料做包裹层的复合防护结构，并通过数值模拟分析了该防护结构对爆炸冲击波的减弱效果。彭佳等[8]针对小当量的爆炸物，提出了一种由复合材料和水溶液组成的柔性防护结构，研究表明，柔性防护结构能有效减小冲击波的超压峰值，增加正压作用的时间。袁天等[9]开展了钢板/Kevlar 层合结构爆炸响应的数值模拟研究，发现增加Kevlar 层对单一钢板的抗爆性能起到了明显的增强作用。徐斌等[10]通过数值模拟研究了爆炸冲击波与防弹衣的相互作用，结果表明，爆炸冲击波与防弹衣发生相互作用形成的复杂波系会加重对人体的损伤。邵先锋等[11]设计了一种由泡沫铝、水溶液、Kevlar 材料复合而成的柔性结构，并通过AUTODYN 数值模拟软件分析了防护性能，结果表明，柔性结构能有效降低冲击波的压力。苗成等[12]通过陶瓷复合装甲抗爆轰性能试验，发现陶瓷复合装甲结构可以有效降低爆轰压力。王燕等[13]设计了由聚脲(polyurea，PU)、防爆液体和纤维材料组成的复合柔性防护结构，通过数值模拟研究了PU 材料在不同位置和厚度不同时该结构的抗破片侵彻性能。张玉玉等[14]采用边长为3 mm 的立方块钨金破片，研究了军用防弹衣和Q235 钢板对破片的防护性能。Han 等[15]实验研究了不同步枪子弹冲击硬/软复合材料时明胶块的瞬态压力，并比较了子弹类型对瞬态压力波参数的影响。唐昌州等[16]通过数值模拟研究了Kevlar 与超高分子量聚乙烯(ultra high molecular weight polyethylene，UHMWPE)混杂配比对防弹衣抗侵彻性能的影响，发现与单一Kevlar 制作的防弹衣相比，采用面板Kevlar、背板UHMWPE 混杂结构的防弹衣抗侵彻性能更好。李茂等[17]对芳纶纤维增强复合装甲结构抗侵彻性能进行了实验研究，发现芳纶纤维与覆盖钢板之间的间隙可以提高纤维层的抗侵彻能力。综上所述，目前对于胸部防护的研究多基于单独爆炸冲击波或破片的防护，对冲击波与破片联合作用下胸部防护的研究较少。

基于复合结构优异的抗冲击和防爆性能，本文中设计一种由PU、Kevlar 和发泡聚丙烯泡沫(expanded polypropylene，EPP)组成的复合防护结构，用于防御爆炸冲击波与破片的联合作用，并通过流固耦合数值计算方法探讨不同排布类型和厚度对复合结构防护效果的影响。

1 数值模拟

1.1 模型建立

采用任意拉格朗日-欧拉(arbitrary Lagrange-Euler，ALE)算法模拟爆炸冲击波和破片与防护结构的相互作用，整体有限元模型如图1(a)所示。空气及炸药网格单元采用ALE 算法，其余部分采用拉格朗日网格划分。空气域尺寸为930 mm×130 mm×130 mm，空气域网格单元尺寸为2 mm×2 mm×4 mm。为了提高计算的准确性，对炸药和防护结构附近的空气网格进行加密，单元尺寸为2 mm×2 mm×2 mm，空气域网格单元共1 094 275 个。在起爆点的X、Y和Z等3 个方向设置对称边界，空气域其余三个面为无反射边界，以此模拟无限流域。

图1 有限元模型Fig.1 Finite element model

炸药源采用圆柱形简易爆炸装置(improvised explosive device，IED)模拟，如图1(b)所示，起爆点设置在IED 中心，距离防护结构0.5 m。炸药当量为100 g TNT，半径20 mm，高48.8 mm，外部包裹168 颗大小和质量均相同的钢制小球充当破片，小球半径3 mm、质量0.882 g。

防护结构由Kevlar、PU 和EPP 组成。由于靠近人体结构的一侧多采用软质材料，因此最里层选用EPP 材料。设置3 种排布组合：Kevlar-PU-EPP、PU-Kevlar-EPP 和PU-Kevlar-PU-EPP。3 种组合结构的尺寸为240 mm×240 mm×26 mm，其中，Kevlar 厚度为10 mm，EPP 厚度10 mm，单层PU 结构中PU 的厚度为6 mm，双层PU 结构中每层PU 的厚度均为3 mm。3 种结构的模型如图1(c)所示。

当冲击载荷通过不同排布类型的防护结构时，传递的冲击压力也会不同。因此，为表征防护结构的缓冲性能，参考Yang 等[18]的研究建立了透射压力测试平台（模拟胸部所受负载），如图1(d)所示。压力测试平台由圆柱形压力传感器、硅胶、泡沫和钢架组成，压力传感器直径为6 mm，长30 mm，硅胶尺寸为280 mm×244 mm×244 mm，泡沫尺寸为120 mm×244 mm×244 mm，钢架厚度为3 mm。由于本文模型采用对称约束，并且有破片冲击，因此压力传感器置于测试平台中间对称面，距离硅胶冲击面10 mm。

1.2 材料模型

Kevlar 具有正交各向异性的特点，因此采用LS-DYNA 软件的MAT22 号复合材料，该材料采用损伤本构模型COMPOSITE_DAMAGE 进行描述，能较好地模拟正交复合材料的失效，其应力-应变关系为：

式中：ε 为正应变，γ 为切应变，σ 为正应力，τ 为切应力，G为剪切模量，E为杨氏模量，下标1、2、3 表示材料的弹性主方向。

该材料模型将纤维的失效形式分为4 种。

(1) 纤维的拉伸失效

式中：Xt为纵向拉伸强度，Sc为面内剪切强度，δ 为失效参数。

(2) 纤维的压缩失效

式中：Xc为纵向压缩强度。

(3) 基体的拉伸失效

式中：Yt为横向拉伸强度。

(4) 基体的压缩失效

式中：Yc为横向压缩强度。

Kevlar 材料的参数如表1 所示。其中：ρ 为密度，µ为泊松比，Kf为失效体积模量，α 为剪切应力参数，SN为法向拉伸强度，S13和S23为横向剪切强度。

表1 Kevlar 材料参数[19]Table 1 Parameters of Kevlar [19]

PU 材料有很明显的应变率效应，采用MAT24 号多线段弹塑性材料模型，该模型能够定义断裂应变值以及输入应力-应变曲线，依据Cowper-Symonds 理论，通过动力放大系数来考虑材料的应变率效应。动力放大系数为：

式中：ε ˙为应变率，C和n为应变率参数，当C和n为0 时，忽略应变率效应。MAT24 号材料模型选择黏塑性公式，此时动态屈服应力为：

PU 材料的性能参考文献[20]的实验数据，如图2(a)所示，其他材料参数如表2 所示。

表2 PU 材料参数[20]Table 2 PU parameter[20]

图2 PU 和EPP 的应力-应变曲线[20-21]Fig.2 Stress-strain curves of PU and EPP[20-21]

EPP 采用MAT57 号材料，该材料采用卷积形式的线性黏弹性模型，对于低密度高压缩性的泡沫材料具有较好的模拟效果。线性黏弹性模型如下：

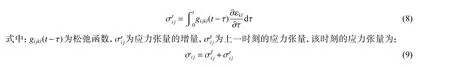
计算中采用Prony 级数形式的松弛函数：

该松弛函数通过输入杨氏模量E和衰减系数β1来定义材料的应变率效应。材料模型只需输入准静态应力-应变关系曲线即可，材料参数确定相对简单。根据团队前期实验结果[21]，EPP 密度为0.03 g/cm3，弹性模量为2.56 MPa，其应力-应变曲线如图2(b)所示。

选用TNT 炸药，采用MAT8 号材料以及JWL 状态方程:

式中：p为爆轰压力，V为初始相对体积，E0为体积爆轰能量，A、B、ω、R1、R2为多项式方程系数，参数值如表3[22-23]所示。

表3 TNT 炸药材料及状态方程参数[22-23]Table 3 TNT explosive materials and state equation parameters[22-23]

空气选用MAT9 号材料，状态方程采用* EOS_LINEAR_POLYNOMIAL：

参数值如表4[24]所示。

表4 空气材料及状态方程参数[24]Table 4 Air materials and state equation parameters[24]

由于小球冲击防护结构后变形较小，因此小球材料采用线弹性模型MAT1，ρ=7.8 g/cm3，E=208 GPa，µ=0.3。压力测试平台的部分材料参数参考Yang 等[18]的研究数据，压力传感器、硅胶和钢架均采用线弹性模型MAT1，压力传感器和钢架的材料参数相同，ρ=7.8 g/cm3，E=210 GPa，µ=0.33；硅胶密度ρ 为1.1 g/cm3，E=43 MPa，µ=0.495；泡沫采用EPP 材料。

为模拟Kevlar 材料的分层，采用CONTACT_TIEBREAK_SURFACE_TO_SURFACE 接触模拟分层现象。相较于普通接触，tiebreak 接触不仅可以承受压力，还可以承受拉力，其失效准则为：

式中：σn为法向应力，σs为切向应力；σNL和σSL分别为层间法向强度和切向强度，参考文献[25]分别取为93 和45.8 MPa。

1.3 模型验证

为验证Kevlar 材料模型的有效性，对文献[26]中的实验进行模拟再现。实验中所用的平头弹半径为5 mm，高为20 mm，靶板的长和宽均为150 mm，厚度为5、10 mm。子弹所用材料为钨，密度19.35 g/cm3，由于子弹冲击靶板时几乎不变形，因此子弹采用刚体材料模型。由于整个模型对称，因此建立1/4 模型，分别采用对称边界和完全固定边界。

对入射速度为218、254 m/s 的2 组实验进行数值模拟，数值模拟后的剩余速度与实验的剩余速度对比如表5 所示。由表5 可知，数值模拟结果略小于实验结果，主要是由于实验中子弹入射时存在倾角，而子弹入射倾角会影响其侵蚀能力，数值模拟中是垂直入射，所以模拟与实验有一定误差，但误差较小，验证了Kevlar 模型的有效性。

表5 模型验证剩余速度对比Table 5 Residual velocity comparison for model validation

PU 模型参考文献[27]验证。根据文献中的铝板冲击实验，建立子弹冲击铝板模型。铝板尺寸为170 mm×170 mm，子弹为直径37 mm 的圆柱形弹体，长度为500 mm。由于模型对称，因此建立四分之一模型，分别采用对称边界和固定边界。文献中子弹材料为45 钢，在实验中几乎无变形，其受力变形的情况可以忽略，因此子弹采用刚体材料模型，ρ=7.85 g/cm3、E=200 MPa、µ=0.32。铝板采用MAT3 号材料，ρ=2.7 g/cm3、E=68 GPa、µ=0.33，屈服应力为75 MPa、切线模量为4620 MPa。

结构为单一铝板结构和涂层结构，其中涂层结构分为前涂层和背面涂层，对子弹速度为14.2 m/s 的实验进行数值模拟，如表6 所示。

表6 靶板背面中心处最大位移Table 6 Maximum displacement at the back center of target plate

对比实验与数值模拟的最大位移，模拟结果与实验结果很接近，误差在3%以内。图3 为2 种PU 涂层结构的背面中心位移时程曲线。由图3 可知，2 种PU 涂层结构的数值模拟曲线与实验曲线趋势大致相同，峰值位置相近。虽然数值模拟中曲线在达到峰值后出现了一定的偏差，但这主要是因为试验中靶板与固定装置通过螺栓连接，所以子弹冲击时靶板与固定装置连接处会向中心移动，增大了中心处的变形量；另外，试验中所用的子弹较长，发射击中靶板后子弹还停留在滑膛中，板件在回弹过程中需要克服子弹与滑膛之间的摩擦力，因此实验的位移要比数值模拟大，且在回弹部分比数值模拟更加平缓。综上所述，PU 材料模型是相对准确的。

图3 聚脲涂层结构位移时程曲线Fig.3 Displacement-time history curves of polyurea coating structures

2 数值模拟结果分析

2.1 单独爆炸冲击波载荷下防护结构的动态响应

为了比较防护结构在不同载荷下的防护效果，本节模拟单独爆炸冲击波作用下防护结构的力学响应。

2.1.1 爆炸冲击波的传播过程

图4 为爆炸冲击波的传播过程。0.28 ms 时爆炸冲击波在空气介质中传播。0.34 ms 时，冲击波已到达防护结构表面，结构表面在耦合作用下率先开始运动，带动整体变形，并对前方的冲击波进行反射，使得前方空气压力增强。0.48 ms 时冲击波进一步在结构中传播产生应力波，防护结构中间部位压缩变形明显，并对后方压力测试平台进行挤压，透射压力开始增大。0.84 ms 时，空气压力已恢复至大气压，防护结构在惯性力作用下持续对后方压力测试平台进行挤压，压力测试平台透射压力进一步增大。

图4 爆炸冲击波的传播过程Fig.4 Propagation process of blast wave

2.1.2 防护结构的透射压力分析

3 种结构的透射压力变化如图5(a)所示，爆炸冲击波能量先以应力波形式传入各层，防护结构变形，随后各层之间以弹塑性波的形式传播，测试平台压力开始增大。整个过程中，PU-Kevlar-EPP 结构的透射压力峰值最小，为0.282 MPa，其次为PU-Kevlar-PU-EPP 结构，压力峰值为0.287 MPa，Kevlar-PU-EPP 结构的透射压力峰值最大，为0.289 MPa。在单独爆炸载荷下，3 种防护结构的透射压力均小于0.29 MPa；而在无防护情况下，根据爆炸经验公式[28]，0.5 m 处的超压可达0.81 MPa，可见防护结构对冲击波的超压降幅超过64.2%，因此防护结构可以有效降低爆炸冲击波的超压。分析3 种结构冲击面中心的位移，如图5(b)所示，结构先受到挤压，达到最大值时开始回弹。3 种结构中，PU-Kevlar-PU-EPP 和Kevlar-PUEPP 结构的位移几乎相同，PU-Kevlar-EPP 结构的位移更小，表明该结构对爆炸载荷的抵抗能力更好，所以压力测试平台的压力更小。总的来说，单独爆炸载荷下，PU-Kevlar-EPP 结构抗爆性能优于另外2 种结构，防护效果最好。

图5 爆炸载荷下3 种结构的压力时程曲线和结构正面中心位移时程曲线Fig.5 Pressure-time history curves and front center displacement-time history curves of three structures under explosion load

2.2 爆炸冲击波与破片联合作用下防护结构的动态响应

2.2.1 爆炸冲击波与破片的传播过程

图6 为爆炸冲击波与破片的传播过程。由图6 可知，0.44 ms 时，冲击波与破片均在空气介质中传播，但冲击波传播速度比破片快。0.50 ms 时，冲击波已到达防护结构表面，结构表面受到冲击带动整体变形，并对前方的冲击波进行反射，使得前方空气压力增强，此时破片仍在空气介质中传播。0.56 ms 时，破片到达防护结构表面，由于破片以极高的速度冲击，结构受到进一步压缩变形。0.68 ms 时，空气压力已恢复至大气压，破片持续冲击防护结构使得结构前几层被击穿，压力测试平台的透射压力显著增大。

图6 爆炸冲击波与破片的传播过程Fig.6 Propagation process of blast wave and fragments

2.2.2 防护结构的透射压力分析

防护结构的动态响应如图7 所示，在爆炸冲击波与破片联合冲击下，防护结构先受到爆炸冲击波的冲击，随后受到破片的侵彻并产生压缩波和拉伸波，部分纤维发生分层破坏。当破片进一步侵彻时，纤维开始逐层发生拉伸断裂破坏，纤维的分层破坏也进一步加重，同时PU 层和泡沫层的变形不断增大，测试平台压力逐渐上升。可以看出，防护结构通过自身的变形吸能及提供层间剪力的方式抵抗爆炸冲击从而进行爆炸防护。

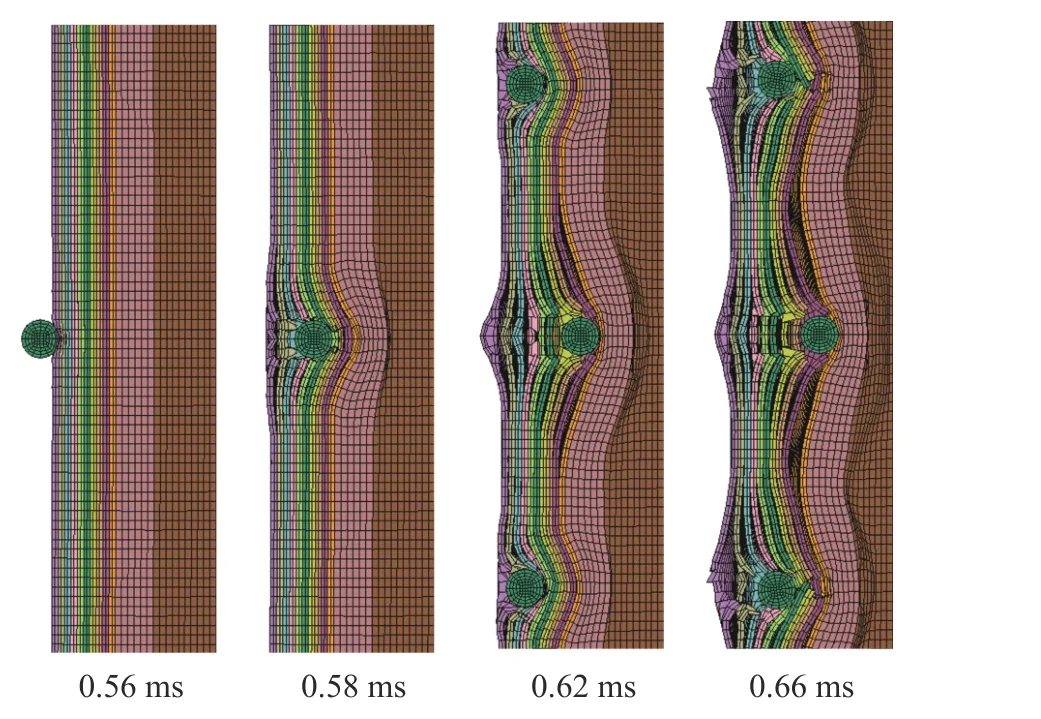
图7 联合载荷下防护结构的动态响应Fig.7 Dynamic response of protective structure under combined action of blast wave and fragments

3 种结构的透射压力时程曲线如图8 所示。相较于单独爆炸载荷，联合载荷作用下透射压力上升时间较晚，这是因为炸药爆炸时破片吸收了部分爆轰能量，爆炸冲击波对防护结构的冲击程度减小且冲击时间更晚。整体来看，PUKevlar-EPP 结构的透射压力峰值最小，为0.388 MPa，其次是Kevlar-PU-EPP 结构，压力峰值为0.473 MPa，PU-Kevlar-PU-EPP 结构压力峰值最大，为0.476 MPa。总的来说，在联合载荷作用下，物体受到的损伤更为严重，这与已有的研究结论[3-6]是一致的。根据新版GA420−2008 系列标准警用防爆服的耐冲击性能指标，在120 J能量冲击下，相应部件不应破损、开裂。本文中最高速度破片冲击防护结构时动能达到323 J，3 种防护结构均未完全击穿开裂，因此虽然在爆炸冲击波与破片联合作用下防护结构的透射压力增大，但防护结构对冲击波与破片的防护还是有效的。3 种结构中PU-Kevlar-EPP 结构的透射压力最小，表明其防护效果优于另外2 种。

图8 联合载荷下3 种结构的压力时程曲线Fig.8 Pressure-time history curves of three structures under combined action of blast wave and fragments

2.3 PU 厚度的影响

基于PU 材料在抗弹、防爆方面的优势，研究PU 厚度对防护结构在爆炸冲击波与破片联合作用下防护效果的影响。根据Wu 等[22]的研究，6 mm 厚度的PU 吸能效果较好，因此本文中以6 mm 厚度PU 的PU-Kevlar-EPP 结构为基准，Kevlar 和EPP 厚度均为10 mm，比较2、4、6、8 和10 mm 厚度PU 的PU-Kevlar-EPP 结构的透射压力。

数值模拟中，由于2 mm PU 的PU-Kevlar-EPP 结构被破片击穿，因此只提取了另外4 种厚度结构的结果数据。图9 是4 种不同PU 厚度的PU-Kevlar-EPP 结构的透射压力时程曲线，从图中可知，4 mm 厚度PU 结构的透射压力峰值最大，其次是6、8 mm 厚度PU 结构的，10 mm 厚度PU 结构的透射压力峰值最小。4 种结构的压力峰值如图10 所示。从4 mm 到10 mm，PU 厚度每增加2 mm，防护结构的透射压力峰值分别减小25.24%、24.48%和5.80%，表明继续增加厚度对提升防护能力的影响逐渐减弱。在实际应用中，如果只靠增加PU 厚度并不能解决一切问题，反而会使成本增加、结构笨重，因此需要根据实际情况选择合适的PU 厚度才能获得最佳的防护效果。

图9 不同PU 厚度结构的压力时程曲线Fig.9 Pressure-time history curves of different PU thickness structures

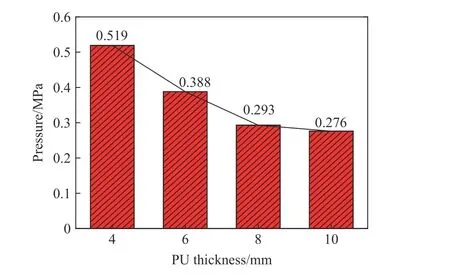
图10 不同PU 厚度结构的峰值压力Fig.10 Peak pressures of different PU thickness structures

3 结 论

通过数值模拟对爆炸冲击波与破片作用下Kevlar、PU 和EPP 组成的复合结构的防护性能进行了研究。通过与文献实验比较，验证了模型的准确性，并得到以下结论。

(1)在0.5 m 距离、100 g 当量TNT 炸药爆炸产生的爆炸冲击波作用下，PU-Kevlar-EPP 结构的透射压力峰值最小，较透射压力峰值最大的Kevlar-PU-EPP 结构峰值减小了2.42%，较无防护时超压降幅超过64.20%，表明防护结构可以有效降低爆炸冲击波的超压，且PU-Kevlar-EPP 结构的抗爆效果优于另外2 种。

(2)在0.5 m 距离、100 g 当量TNT 的IED 爆炸产生的爆炸冲击波与破片联合作用下，3 种防护结构均未被完全击穿，有效抵抗了爆炸冲击波与破片的冲击。其中，PU-Kevlar-PU-EPP 结构的透射压力峰值最大为0.476 MPa，PU-Kevlar-EPP 结构的透射压力峰值最小，为0.388 MPa，减小了18.49%，表明不同的结构排布显著影响防护效果，且PU-Kevlar-EPP 结构的防弹抗爆性能更好。3 种防护结构的透射压力峰值均比单独爆炸下的压力峰值要大，表明联合载荷比单独爆炸导致的损伤更严重。

(3)对不同PU 厚度的复合结构进行了模拟分析，并比较了增强效果，结果表明，随着PU 厚度的增加，透射压力减小，防护结构的防护效果逐渐增强，但继续增加厚度对提升防护能力的影响逐渐减弱。