恒定动载下高温水冷后玄武岩的动力特性及本构模型*

徐泽辉，何 童，杜光钢，刘 磊,3

（1.昆明理工大学公共安全与应急管理学院，云南 昆明 650093；2.昆明理工大学国土资源工程学院，云南 昆明 650093；3.昆明理工大学云南省中-德蓝色矿山与特殊地下空间开发利用重点实验室，云南 昆明 650093）

近年来，岩石材料的高温动态力学特性研究备受学者关注，该课题对矿产资源开发[1]、地热能的开发[2-3]以及地下工程安全防护[4]等领域具有非常重要的工程意义。岩石在地应力、地温、地下水压等环境因素影响下，其力学响应特征会发生改变[5]，而在资源开采过程中，又伴随着高温高压设备、常温钻井液与井壁围岩之间的接触，高温岩体同样会发生水冷却后温度降低的过程，尤其是在热冷作用下，岩石的强度特性发生二次劣化[6]，在受到冲击地压、机械振动和爆破等冲击荷载作用后，更容易诱发碎裂、剥落、岩爆等工程灾害[7-8]，严重制约了资源的安全高效开采。除此之外，地下隧道工程发生火灾爆炸事故进行灭火时，其围岩的力学特性也会受到高温水冷、围压、冲击荷载等多因素影响。因此，开展不同围压下高温水冷后玄武岩的动态力学特性研究，对地下资源开发及地下工程安全防护均有重要意义。

目前，学者们借助分离式霍普金森压杆（split Hopkinson pressure bar, SHPB）实验装置对不同耦合因素下岩石的动态力学性能及本构模型开展了大量研究，并取得了一些进展。诸多学者考虑了温度和冲击荷载耦合因素，如陈腾飞等[9]、Gautam 等[10]、朱要亮等[11]和Yang 等[12]考虑了岩石的动态峰值强度、峰值应变和动态弹性模量的影响，认为当温度低于200 ℃时，温度对岩石的力学性能影响较小；当温度高于200 ℃时，随着温度升高，岩石内部的孔隙和微裂纹增加，岩石的动态强度劣化越严重，动态峰值应变越大。高温条件下，应变率对岩石强度特性的影响更加显著，而不同温度下应变率对岩石的弹性模量和弹性模量增长率的影响不明显。此外，还有学者对岩石的高温动态本构模型进行了相关研究，通过建立合理的损伤本构模型来反映高温作用下岩石损伤的力学机制，其中，Chaki 等[13]利用高温后花岗岩的孔隙度、纵波波速等指标的衰减特征对岩石的整体热损伤进行了评估，建立了考虑热损伤参数的本构模型，并结合理论和实验手段对岩石内部结构的热劣化机制和破坏机制进行了分析。许金余等[14]、Wang 等[15]结合Weibull 分布的统计理论和连续强度理论，构建了大理岩、花岗岩高温动态损伤本构模型，并将理论曲线与实验曲线进行了对比验证，发现其拟合度较好。上述研究从实验和理论角度均证实了热损伤效应对岩石的动态力学性能影响较大，高温动态本构模型的建立方法可为多因素耦合本构模型的建立提供参考。除温度因素外，地下复杂的应力环境对岩石的力学性能也有较大影响，Liu 等[16]、Li 等[17]采用带围压SHPB 系统对不同围压岩石的动态压缩特性进行了研究，分析了围压对岩石动态峰值应力、峰值应变、失效模式的影响，认为随着围压的升高，岩石的动态强度性能增强，逐渐表现出塑性变形特征，在围压作用下，岩石表现出压剪破坏模式。在本构模型方面，刘军忠等[18]、Wang 等[19]分析了围压、应变率对角闪岩、砂岩的动态抗压强度的影响，并建立了相应的动态损伤本构模型，该模型的理论曲线可以较好地表征试样在冲击荷载作用下的力学响应特征。

综上可知，学者们对高温后岩石的动态力学特性及本构模型的研究主要集中在单轴冲击压缩方向，而对主动围压条件下高温水冷后岩石动力特性和本构理论模型的综合研究较少，且在地下资源开发工程中，岩石常处于复杂的水热耦合环境，并受到多维静荷载与动荷载的耦合作用。为更好地开展复杂环境下岩体的动态力学性能研究，满足当前岩石工程的实际需求，本文中，选取广泛分布的玄武岩作为研究对象，利用带围压装置的SHPB 实验系统对不同温度水冷后的玄武岩试样进行动态压缩实验，以探究高温水冷因素与围压因素耦合作用下玄武岩的动态力学特性，并建立高温水冷后玄武岩在不同围压下的动态本构模型，将理论模型与实验数据进行对比，验证所建立模型的合理性和适用性。

1 SHPB 实验

1.1 实验装置

实验采用昆明理工大学带围压SHPB 装置，装置示意图和实验加载步骤如图1 所示。该装置主要由动力系统、杆件系统、数据采集系统和围压加载系统组成。SHPB 实验系统中的杆件和子弹均采用高强度钢，其密度为7 850 kg/m3，弹性模量为210 GPa，泊松比为0.28，纵波波速为5 189 m/s，其中子弹、入射杆、透射杆长度分别为0.4、2.5 和2.0 m，直径均为50 mm。

图1 带围压的SHPB 装置Fig.1 SHPB device with confining pressure loading system

主动围压下，岩石SHPB 动态压缩实验仍需遵循2 个基本原理，即一维应力波理论和应力均匀性假设理论[20-21]。加载过程中，通过超动态应变仪记录入射杆和透射杆上的应变片采集的入射、反射和透射电压信号，再利用三波法[22]对采集数据进行处理，获得试样的应力 σ 、应变 ε 以及应变率 ε˙ ：

式中：εi(t)、εr(t)和 εt(t) 分别为t时刻的入射、反射和透射应变，A0、E0和c0分别为杆件的横截面积、弹性模量和纵波波速，As和Ls分别为试样的横截面积和长度。

选取玄武岩试样在动态压缩实验中最具代表性的原始数据，可处理得到试样的动态应力平衡曲线，如图2 所示。从图2 可以看出，入射波和反射波的叠加波形与透射波的波形几乎重合，说明玄武岩试样两端所受应力基本相等，符合应力均匀性假设，从而保证了实验结果的有效性。

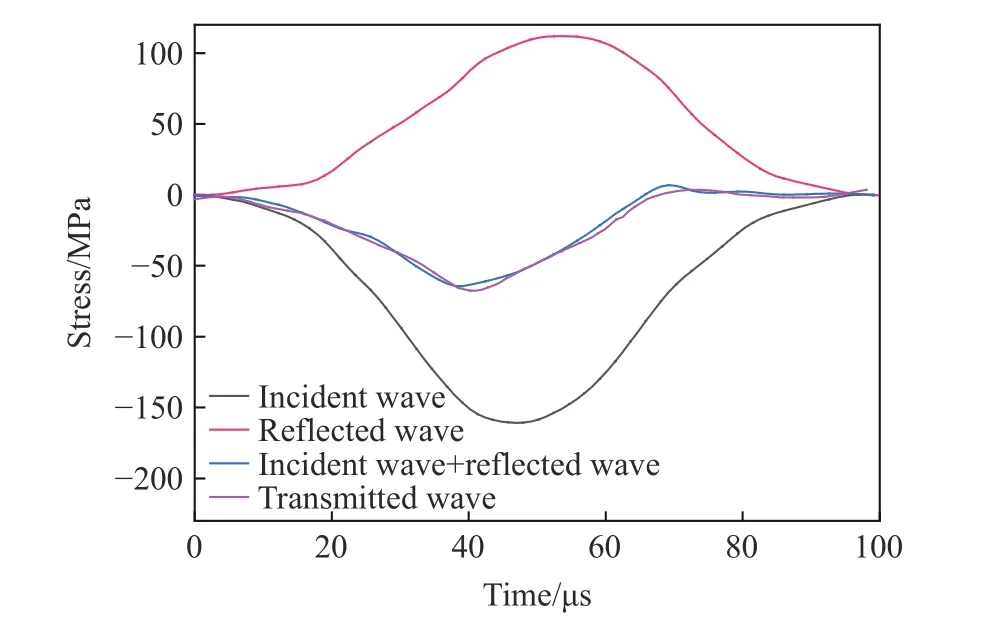
图2 动态应力平衡检验Fig.2 Dynamic stress balance verification

1.2 试样制备

实验所用岩块均为采自云南卡房矿山100～600 m 深处的玄武岩，其均质性较好，无明显节理裂隙。根据国际岩石力学学会（ISRM）的标准，将玄武岩加工成 ∅ 50 mm×30 mm 的圆柱试样。控制试样高度误差小于±0.3 mm，直径误差小于±0.3 mm，端面不平整度小于±0.05 mm。

利用KRX-17B 箱式炉（见图3）将上述圆柱试样分别进行4 组温度（100、300、450 和600 ℃）下的高温水冷处理，并设计一组常温（25 ℃）状态下的圆柱试样进行对比分析。试样升温速率为5 ℃/min，加热至预设温度后保持恒温1 h；恒温结束后，采用自来水充分冷却至常温，随后进行24 h 烘干处理，排除试样含水率对实验的影响。图4 为玄武岩试样经历不同温度水冷处理后的表观形貌，可以看出，随着温度升高，玄武岩试样逐渐由灰绿色转变为红褐色，并在450 和600 ℃时出现微裂纹。

图3 KRX-17B 箱式炉Fig.3 KRX-17B box furnace

图4 玄武岩的表观形貌Fig.4 Apparent morphology of basalt specimens

通过前期物理性质、静态力学特性以及X 射线衍射分析测试，可得到不同温度水冷处理后玄武岩试样的静态应力-应变曲线（见图5）、静态单轴抗压强度、纵波波速及静态弹性模量（见表1）。温度对岩石力学特性的影响可表现在热开裂、矿物含量变化、水分丧失等方面[23]，根据Wu 等[24]开展的X 射线衍射实验和相关研究可知，本实验研究范围内，高温水冷作用并未显著影响玄武岩的矿物组分，说明岩石内部结构热冷损伤产生的裂隙是其基本力学特性发生改变的主要原因。

表1 高温水冷玄武岩的基本物理力学参数Table 1 Basic physical and mechanical parameters of basalt after high-temperature treatment and water cooling

图5 高温水冷后玄武岩静态应力-应变曲线Fig.5 Static stress-strain curves of basalt after high-temperature water cooling

1.3 实验方案

试样温度设置为常温（25 ℃）、100、300、450 和600 ℃共5 个温度等级，同时，为研究试样动力特性的围压效应，结合卡房矿山地应力原位测试相关资料[25-26]，采用控制变量法，在试样每一温度等级下进行3 个围压系列（2、4 和6 MPa）的SHPB 实验，冲击气压控制为1.0 MPa。因此，实验共分为15 组，每组准备3 块试样进行3 次独立重复实验，从中选取最具代表性的数据进行分析。表2 给出了主动围压下高温水冷玄武岩的动态压缩实验结果。

表2 玄武岩动态压缩实验结果Table 2 Results of dynamic compression experiments on basalt

2 实验结果分析

2.1 动态应力-应变曲线特征

图6 为不同围压作用下高温水冷玄武岩的动态应力-应变曲线。由图6 可知，相比于玄武岩的静态压缩应力-应变曲线（见图5），高温水冷后玄武岩的动态压缩应力-应变曲线均不存在压密阶段，这可能是由于预先加载的围压使试样的致密性和弹性增强，且试样受到冲击荷载作用的时间较短，使得试样均未表现出压密特征。因此，本文中，动态应力-应变曲线大致分为线弹性变形阶段、屈服阶段、卸载阶段3 个阶段。

图6 不同围压下高温水冷玄武岩的动态应力-应变曲线Fig.6 Dynamic stress-strain curves of high-temperature water cooling basalt under different confining pressures

从图6(a)～(c)可知，在线弹性变形阶段，围压一定时，随着温度升高，试样内部微裂纹逐渐增多，使试样抵抗变形能力减弱，从而导致该阶段曲线斜率降低；在屈服阶段，曲线应力呈非线性增长趋势，当围压一定时，温度越高，应力增长速率趋缓，曲线的屈服平台更加明显，表明试样塑性逐渐增强；在卸载阶段，当轴向应力达到峰值后，5 组温度试样表现出不同的峰后曲线趋势。当围压一定时，25～300 ℃的试样被破坏后，其应力下降速率较快，应变变化区间较小，整体呈现出脆性破坏特征，而300～600 ℃的试样被破坏后，其应力下降速率减缓，应变量增大，试样的“峰后塑性”更加显著。

当温度一定时，随着围压的升高，试样峰值应力、弹性阶段的斜率逐渐增大。同时发现，围压为6 MPa 时，25～300 ℃下，3 条曲线末尾阶段的变化趋势相比围压为2 和4 MPa 下的曲线有所不同。这主要是由于在25～300 ℃温度区间内，试样内部结构热冷损伤裂隙较少，在冲击荷载作用下破坏程度较轻，仍留有一定的承载能力。在上述前提下，较低围压作用下，试件弹性储能较小，进入卸荷阶段后，卸载力要一直大于试样内部弹性力，因此曲线末尾表现为正常的负效率卸载。较高围压（6 MPa）使得试样在加载过程中储存的弹性能较大，进入卸荷阶段后，卸载力小于试样内部弹性力时，其弹性能将会被释放，使得曲线卸载阶段末尾出现局部应变减小的现象，因此曲线末尾表现为竖直卸载。当试样经450～600 ℃高温水冷处理后，不同围压下曲线均表现出明显的峰前屈服特征和峰后延性特征，说明该温度区间内，试样内部结构热冷损伤裂隙较多，遭受冲击后的残余承载能力较弱，围压作用下塑性特征更显著。

2.2 试样动力特性的温度效应

由图7 可得，在相同围压作用下，玄武岩试样的动态峰值应力（σp）、动态弹性模量（Ed）与温度（T）之间均呈线性关系，即随着温度升高，试样的动力特性均呈劣化趋势。

图7 玄武岩动力特性随温度的变化Fig.7 Variation of dynamic mechanical properties of basalt with temperature

以常温（25 ℃）状态下试样的动态峰值应力作为参考，2 MPa 围压作用下，4 组温度（100、300、450和600 ℃）水冷后，试样动态峰值应力的降幅分别为8.57%、19.88%、38.99%和58.99%；4 MPa 围压作用下，降幅分别为9.69%、13.90%、35.95%和61.25%；6 MPa 围压作用下，降幅则分别为13.98%、23.35%、38.55%和64.21%。分析可知，试样的动态峰值应力随温度升高逐渐降低，且围压越高，温度效应越显著，其主要原因为：作用温度越高，试样内部因矿物差异性膨胀变形所产生的热应力越大，导致内部新生裂纹增多，同时，试样矿物相对含量的变化和水的冷淬对热损伤起到了加剧的作用，3 种影响机制相互竞争，造成了玄武岩试样动态峰值应力的下降。

动态弹性模量是衡量岩石在受到动荷载作用时抵抗变形能力强弱的指标，参考李夕兵等[27]的研究方法，本文中，将应力-应变曲线上峰值应力50%时的应力与其对应的轴向应变的比值作为试样的动态弹性模量。与常温（25℃）状态下试样的动态弹性模量相比，2 MPa 围压作用下，4 组温度（100、300、450 和600 ℃）水冷后，试样动态弹性模量的降幅分别为10.90%、27.80%、45.02%和70.92%；4 MPa 围压作用下，降幅分别为15.94%、27.54%、44.75% 和71.89%；6 MPa 围压作用下；降幅分别为10.78%、26.75%、45.75%和74.08%。由此可得，在相同围压条件下，随着温度升高，试样的动态弹性模量呈劣化趋势，且劣化程度逐渐加剧。究其主要原因，可能为试样在受到高温水冷损伤后，内部微缺陷增多，与常温状态相比，其弹性变形阶段所储存的弹性能减少，使得试样抵抗变形的能力减弱。

2.3 试样动力特性的围压效应

图8 为不同温度玄武岩的动态峰值应力、动态弹性模量随围压的变化，从图8 可知，以2 MPa 围压作用下试样的动力特性作为基准，6 MPa 围压作用下，5 组温度（25、100、300、450 和600 ℃）水冷后，玄武岩的动态峰值应力和动态弹性模量增幅分别为53.69%、44.60%、47.04%、54.81%、34.12%和75.42%、75.66%、77.97%、73.10%、56.39%。由此可知，常温（25 ℃）和经历不同温度（100、300、450 和600 ℃）水冷后，试样的动力特性均存在围压强化效应，即在温度一定时，随着围压的增大，试样动态峰值应力和动态弹性模量均呈现增大的趋势，表明围压在一定程度上可抑制试样内部裂纹的扩展，提高试样内部基元体的强度，使其动力特性显著增强。然而，不同温度水冷后试样动力特性的围压强化效应存在差异，如在6 MPa 围压作用下，25 ℃试样的动态峰值应力和动态弹性模量增幅分别为53.69%和75.42%，600 ℃试样增幅则分别为34.12%和56.39%。表明600 ℃试样动力特性的围压强化效应均弱于25 ℃试样，这主要是由于经600 ℃高温水冷作用后，试样内部热、水冷损伤严重，裂纹扩展贯通程度高，在围压作用下，其内部储存的弹性能较少。因此，600 ℃试样动力特性的围压强化作用相比于25 ℃试样有所减弱。

图8 玄武岩动力特性随围压的变化Fig.8 Variation of dynamic mechanical properties of basalt with confining pressure

2.4 围压和温度对砂岩破坏特征的影响

图9 给出了不同围压、不同温度作用下玄武岩试样的动态破碎特征。可以看出，围压一定时，温度越高，玄武岩试样破坏越严重。这是由于试样经高温水冷处理后内部会产生损伤裂隙，在荷载作用下，发生破坏所需要吸收的能量会降低。因此，在相同荷载作用下，初始损伤裂隙越多的试样，其裂纹发育和衍生的速度更快、更彻底。

图9 不同围压和温度作用下玄武岩试样的动态破坏特征Fig.9 Dynamic failure characteristics of basalt specimens at different confining pressures and temperatures

温度一定时，随着围压升高，玄武岩试样的破碎程度逐渐降低。这是由于围压在一定程度上可为试样提供径向约束力，限制了试样内部裂纹的扩展，围压越高，约束作用越强，试件的破坏程度越低。同时发现，围压为6 MPa 时，25、100 和300 ℃试样由于内部储存了大量的弹性能，在受到冲击荷载作用后均未完全破碎，与上述实验结果中应力-应变曲线卸载阶段应变减小现象相对应。

3 恒定动载下高温水冷后玄武岩的动态本构模型

3.1 高温水冷损伤演化方程

在高温作用下，由于岩石分子发生热运动及矿物颗粒之间发生不协调热膨胀变形，使得岩石内部产生热应力，当热应力大于矿物极限强度时，岩石则会产生新生裂纹，且温度梯度越大，产生的微裂纹越多。在热损伤基础上进行水冷作用后，岩石内部损伤加剧，从而导致其力学性能进一步劣化。根据宏观损伤力学理论，可采用弹性模量的变化来表征岩石的高温水冷损伤[28]：

式中：DT为岩石高温水冷损伤变量，EJT为T温度水冷后岩石的静态弹性模量，EJ0为岩石的初始静态弹性模量。

本文中所考虑的岩石高温水冷损伤变量主要受温度变化的影响，依据不同温度水冷后试样的静态弹性模量来计算，与动态实验中的冲击气压和围压无关。

3.2 动荷载损伤演化方程

假设岩石由大量不同强度、不同缺陷的基元体组成，从细观方面分析，各基元体的尺寸需足够大，能包含微裂纹、孔隙等微缺陷，而从宏观方面分析，由于岩石受荷加载的过程为一个损伤连续的过程，所以各基元体的尺寸需足够小，小到可视为连续损伤力学层面的一个质点进行处理。这样既能在细观上满足弹性力学的基本定律，也能保证推导的严密性。因此，可作如下假设。

(1) 岩石在宏观上表现为各向同性，即为各向同性损伤体，在破坏前服从胡克定律，呈线弹性状态。

(2) 基于岩石材料的非均匀性特点及岩石内部各基元体力学特性概率性分布的考虑，假设岩石强度满足Weibull 分布[29]，其概率密度函数为：

式中：ε为岩石受荷时的应变；m和 α 均为Weibull 分布参数，表征岩石损伤演化的特征。

岩石在外荷载作用下，其内部基元体发生持续累积性破坏，而基元体最终的破坏将会导致岩石发生损伤，造成其宏观力学性能降低[30]。因此，为了反映岩石的损伤演化过程，可定义其荷载损伤变量Dε为岩石中已破坏的基元体数目n与总基元体数目N的比值，即：

式中：n为岩石因受荷达到某一应变水平时基元体发生破坏的数目，而在任意区间[ε′，ε′+dε′]内发生破坏的基元体数目为NP(ε′)dε′，当加载到某一应变ε时，则有：

联立式(5)～(7)，化简可得岩石动荷载损伤演化方程：

3.3 本构模型的建立

根据上述假定，岩石试样宏观上表现为各向同性，且初始状态相一致，则岩石试样在高温水冷和动荷载作用下的损伤发展过程如图10 所示。根据损伤力学和应变等价原理[31]，岩石在高温水冷和动荷载耦合作用下的总损伤变量D为：

将式(4)和(8)代入式(9)，化简可得：

根据连续损伤力学理论[32]，在主动围压作用下，岩石高温水冷动态损伤本构方程可表示为：

式中：ED0为岩石初始动态弹性模量，µ为 泊松比，σ3为围压荷载。将式(10)代入式(11)，可将本构方程改写为：

式(12)为主动围压作用下玄武岩高温水冷动态损伤本构模型，该模型综合考虑了高温水冷、冲击荷载及围压等因素。由上述本构方程和实验数据可得，高温水冷作用会对岩石造成损伤，从而降低岩石的动态强度，表现出温度劣化效应，而主动围压可为试样提供径向约束力，从而增强岩石的动态强度，体现了围压强化效应。另外需强调的是，在本文中的研究范围内，玄武岩高温水冷损伤变量DT主要受温度和水冷的影响，为应变率无关量，且该变量是利用试样在静载条件下所测得的弹性模量来计算的。玄武岩荷载损伤变量Dε则主要受冲击荷载力的大小、作用温度及围压的影响，本文中，将每组实验的冲击气压均设定为1.0 MPa，则每组试样应变率的变化皆由温度、围压引起，因此，为考虑应变率对荷载损伤变量Dε的影响，依据文献[33]的研究，将与Dε相关的动力特性参数都视为应变率的相关量，即依据不同应变率下的峰值应力、峰值应变和弹性模量等参数，利用数值拟合方法得到上述动力特性参数与应变率的关系式，从而得到不同应变率下的荷载损伤变量Dε。因此，上述本构方程虽然是在静态力学的基础上构建的，但在本文中的研究范围内也适用于动态力学方面的推导。

3.4 本构模型的参数及验证

为验证上述玄武岩高温水冷动态损伤本构模型的准确性，需确定的参数有ED0、EJ0、EJT、α、m、µ及σ3。其中动态弹性模量参数ED0、静态弹性模量参数EJ0和EJT均可直接通过实验数据获取；σ3则根据每组实验过程中所施加的围压值来确定；泊松比 µ 可由岩石单轴抗压实验确定；Weibull 分布参数 α 和m可采用极值法进行求解，即根据高温水冷玄武岩的动态应力-应变曲线，获得其相应的峰值应力 σc和峰值应变 εc，再利用应力-应变曲线的边界条件求出，即应力与应变之间存在以下几何关系：

根据应变等价假设，可得高温水冷后玄武岩的受荷损伤本构方程为：

式中：EDT为岩石温度水冷后的动态弹性模量。将式(8)代入式(14)，高温水冷后玄武岩的受荷损伤本构方程可改写为：

再利用式(13)中应力与应变之间的几何关系可得：

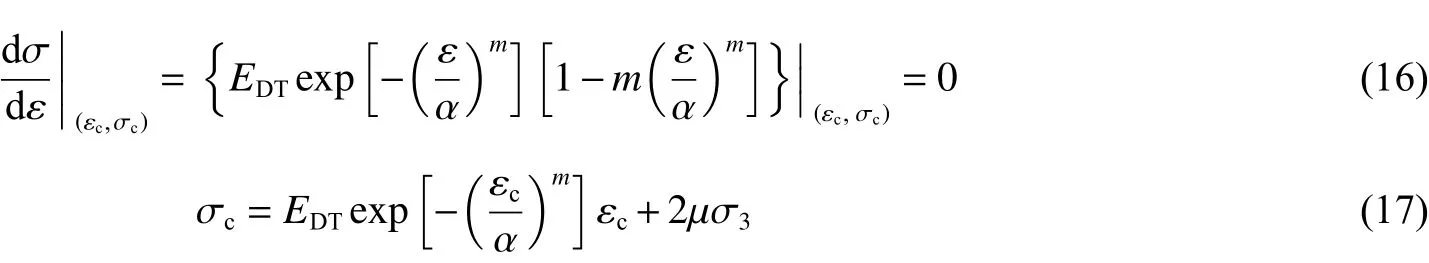
联立式(16)和(17)，可以得到Weibull分布参数α和m：

利用式(12)所建立的本构模型、本构模型相关参数计算方法、静压实验数据以及围压下高温水冷玄武岩动力学实验数据，可确定本构模型参数，如表3 所示。

表3 本构模型参数Table 3 Constitutive model parameters

由图11 可以看出，在不同组合加载条件下，高温水冷动态损伤本构模型所计算出的理论曲线与实验曲线总体上具有较好的一致性，尤其是在曲线的上升阶段，理论曲线所表征的弹性模量、峰值应力和峰值应变等特征与实验曲线特征的匹配程度较高，说明所建立的本构模型可以较好地反映玄武岩动态力学特性与温度、围压之间的关系，在一定程度上验证了该本构模型的合理性。但是在曲线峰后下降阶段，由于岩石在发生破坏后破碎块度分布的随机性和在高围压作用下的峰后回弹特性，导致理论曲线与实验曲线在残余承载力和峰后趋势方面存在一定偏差。因此，未来还需对该高温水冷动态损伤本构模型进行更进一步研究。

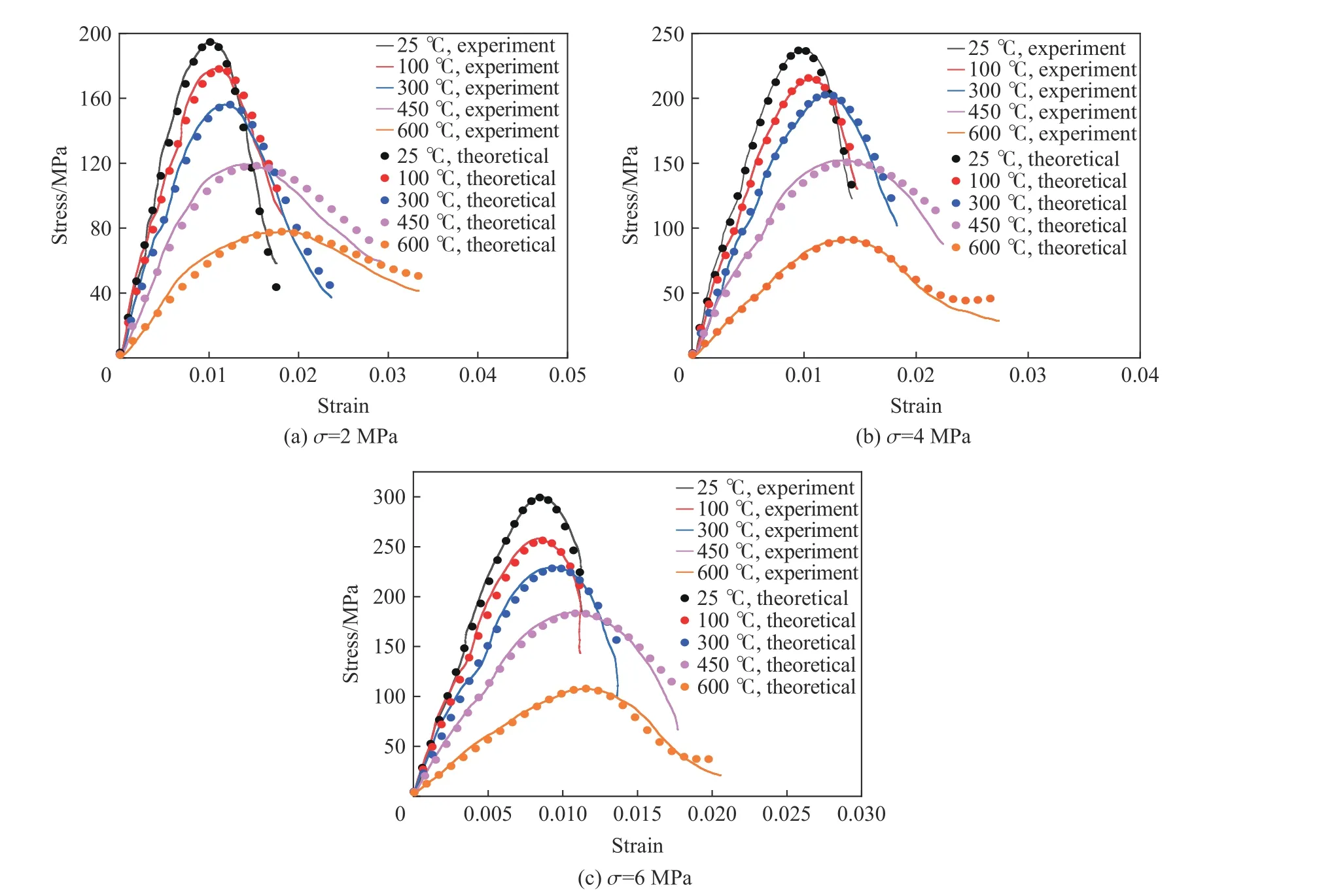
图11 玄武岩的应力-应变实验曲线与理论曲线Fig.11 Experimental and theoretical stress-strain curves of basalt

4 结 论

利用带围压SHPB 实验系统对常温（25 ℃）和高温（100、300、450 和600 ℃）水冷后的玄武岩进行了3 组围压（2、4 和6 MPa）下的动态压缩实验，分析了温度和围压对玄武岩动力特性及破坏特征的影响，并构建了相应的理论本构模型，得到以下主要结论。

(1) 在本文中的研究范围内，随着温度升高，试样的应力-应变曲线在线弹性变形阶段的斜率降低，屈服阶段平台越渐明显，表明玄武岩塑性特征逐渐增强；温度一定时，试件的峰值应力、弹性阶段斜率与围压荷载呈正相关。

(2) 围压一定时，随着温度升高，试样的动态峰值应力、动态弹性模量逐渐降低，且围压越高，温度劣化效应越显著；不同温度水冷后，玄武岩试样的动力特性均存在围压强化效应，但600 ℃下围压强化作用相比于25 ℃试样有所减弱。围压一定时，随着温度升高，试样的破碎程度不断加剧；温度一定时，随着围压的升高，试样的破碎程度逐渐降低。

(3) 本文中所建立的玄武岩动态本构模型参数少、易于求解。理论曲线与实验曲线吻合度较高，该本构模型可较好地反映出玄武岩动态力学特性与温度、围压之间的关系，可用于预测玄武岩在高温水冷和主动围压耦合作用下的动态力学行为，从而为地下资源开发及地下工程防护提供理论支持。