基于液桥力分析的丝网印刷电子转墨率预测模型构建与仿真研究

许建林,任 铮,潘云霄,恩溪弄,李 艳*

(1.北京印刷学院 机电工程学院,北京 102600;2.北京印刷学院 数字化印刷装备北京市重点实验室,北京 102600;3.北京印刷学院 印刷装备北京市高等学校工程研究中心,北京 102600)

近年来,印刷电子技术广受各个领域的关注,该技术利用传统印刷工艺印刷导电油墨来制备电子器件,可实现电子器件的大批量、低成本制造[1],使得传统印刷焕发了新的活力.在众多印刷电子方式中,丝网印刷电子具备承印物限制少、印品墨层厚、电学性能好等优点[2],故而有很高的研究与应用价值.

在保证印制品拥有良好的电学性能方面,印刷电子技术有着较之传统印刷而言更为严格的各项评价标准.在这些标准中,转墨率这一重要指标代表着印刷工作效率的高低,同时也直接关系到印品导电性能的好坏.

本文对丝网印刷电子油墨转移的过程进行深入的机理研究,探究网版回弹过程中液桥断裂的影响因素,基于液桥力变化分析提出了一个转墨率的预测模型,并运用ANSYS Fluent进行CFD仿真验证,结果可靠,为探究转墨率影响因素的相关工作提供了参考.

1 丝网印刷电子转墨率的影响因素

1.1 转墨过程机理分析

正如印刷电子的定义一样,丝网印刷电子是用丝网印刷的方式生产电子元器件的技术,即刮刀推动网版上的导电油墨,使其通过网孔落在承印物上,随后网版回弹使得大部分油墨留在承印物的过程.油墨自网版转移至承印物上的过程称作转墨过程,而成功转移至承印物上的油墨量与填墨总量的比值称为转墨率.

在印刷电子中,转墨率不仅代表着印刷效率的高低,还有着特殊的含义.刘世朴等[3]指出,在丝网印刷电子中,导电油墨在承印物上分布越均匀,油墨厚度越厚,印刷电子产品性能就越好,这就需要保证承印物上有足够的落墨量,即保证较高的转墨率.多年来,为提升印刷效率,业内不乏对转墨过程中提高转墨率进行的多方面研究,但它们大多停留在经验与实验阶段,对转墨过程的深入机理研究则相对较少且较为分散.

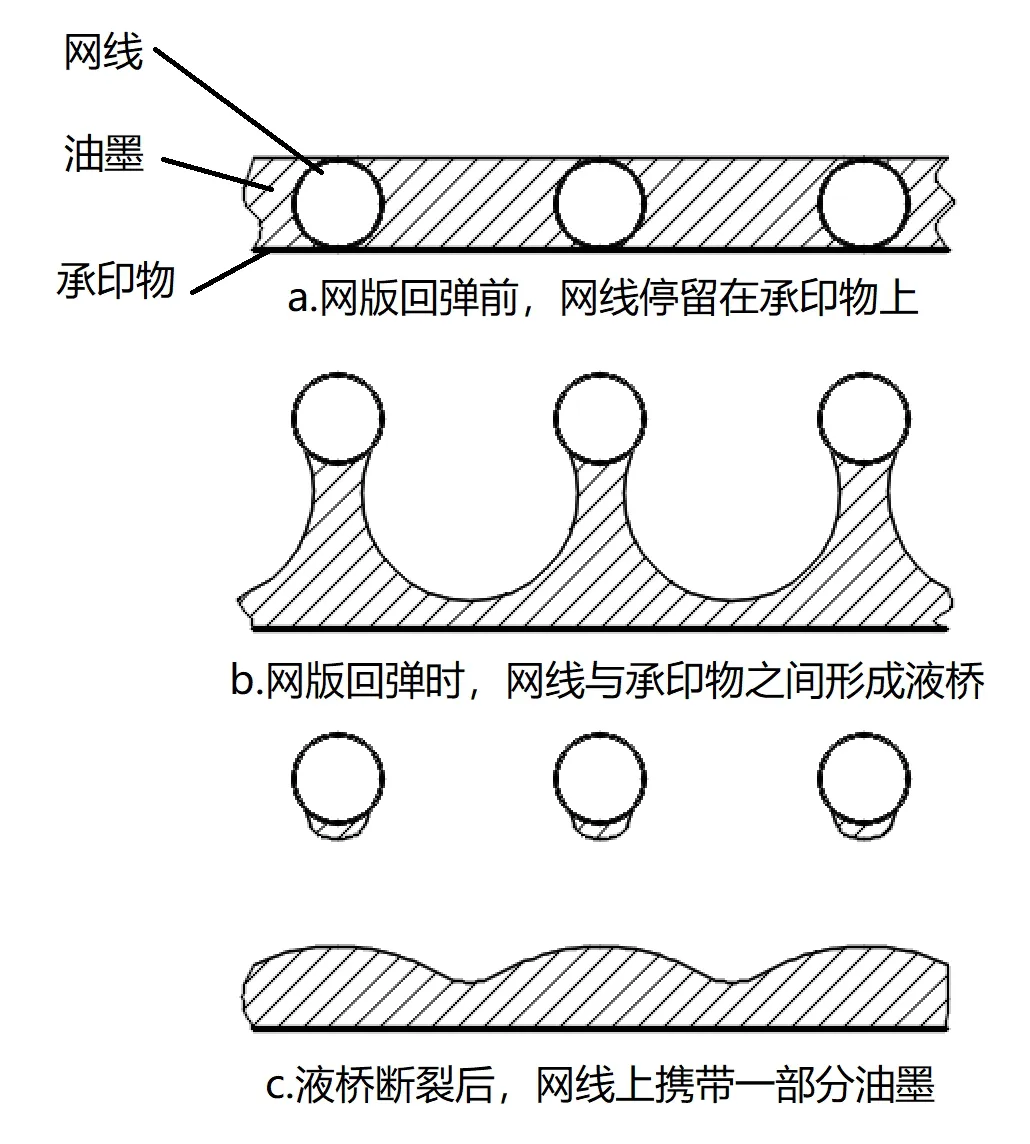
图1 丝网网版回弹过程中的液桥变化示意图

Kapur等[4]首次具体地描述了丝网印刷转墨过程对转墨率的影响,其文中指出最为影响转墨率的过程是网版回弹时由网线带动所引发的油墨表面演变过程,该过程中落在承印物上的部分油墨流向网版并附着在网线上,最终随着网版回弹被带离承印物,即造成了填充油墨的损失.而Kumar[5]则更加直观地描述了这个过程——油墨在网版与承印物之间形成了液桥(Liquid Bridge),液桥不断演变最终断裂,断裂的两部分分别留在网版及承印物上,如图1所示.由此可知,深入研究液桥特性应是探究转墨率影响因素的核心.

1.2 转墨过程液桥变化分析

液桥通常是指形成于另一流体相中的、连接上下两个分离表面之间的液柱.液柱的表面通常是曲面,以保持液体的表面张力与其内部压力平衡.

在丝网印刷过程中,液桥形成于网线与承印物之间,随着网版不断上升,网线与承印物上的油墨之间的第二流体相(即空气相)所占空间会越来越大,液桥在拉伸方向延展的同时在垂直于拉伸的方向上收缩.此过程伴随着液桥内部的液体流动,产生了流体动压的梯度变化.两流体相表面的受力平衡状态由此发生改变,导致液桥表面被外部气压压成内凹的双曲面形状,而这种凹陷的程度会随着网版抬升高度的增加而愈演愈烈.

因此,随着网版的抬高,液桥的演变表现为:液桥长度增加,表面内凹,导致液桥不断颈缩直至在最小截面处断裂成两截,随后两截液桥表面迅速坍塌成表面能量最低的形态并留在了各自所黏附的表面上,至此液桥的演变结束并完成了液体转移.

纵观整个过程,液桥的断裂行为是液桥液体转移过程的核心,若能够描述液桥断裂行为,准确计算出液桥断裂时的各项几何参数,便可通过几何关系推导出转移油墨的体积,进而预测出转墨率.

2 转墨率预测模型的建立

2.1 基于液桥力分析的液桥断裂模型建立

在液桥演变期间,始终存在着维持液桥形态的力——液桥力(Liquid Bridge Force),换言之,液桥断裂的时刻就是最小截面处率先无法维持液桥形态,即液桥力为零的时刻.因此,可从最小截面处液桥力变化情况的角度分析液桥的断裂行为.

为了能够清晰直观地描述出液桥力,需要建立具有清晰几何关系的模型.Butt等[6]在其研究成果中指出了液桥力的计算与上下表面的形状有关,并据此总结了多种液桥成型条件下液桥力计算的几何模型与公式,如平面与平面之间、平面与球面之间等.丝网印刷转墨时液桥形成于网线与承印物之间,本应属于平面与圆柱面之间液桥的类型,但实际情况并不是这样.

Potts等[7]展示了用高速相机对丝网印刷过程的拍摄结果,如图2所示,由于两根网线之间的间距(即网孔直径)相对较小,一根网线上的液桥表面会被相邻网线干涉,液桥表面最终并不会直接与承印物接触,即液桥实际上是形成于固相与液相之间的.但Butt等给出的公式是液桥上下两端均与固相直接接触的,如图3所示[6],这就导致了原本可由油墨与上下表面的接触角θ1、θ2来完成计算的公式并不适用于描述丝网印刷过程中产生的液桥,因为该液桥下表面直接与液相相连,根本没有下表面接触角,因此无法直接套用Butt等的计算公式,需要另外再建立模型.

本文建立的液桥模型如图4所示.在图4中,该模型做了一定的简化处理,将液桥纵向截面的表面轮廓视作半径为R的弧线;r为液桥最小截面半径,θ为油墨与网线之间的接触角,β为液桥在上接触表面处的填充角(在本模型中表现为纵向截面内,液桥表面在网线上的接触点与网线截面圆心的连线同垂直方向的夹角),h为网线抬升高度,H为纵向截面内液桥表面在网线上的接触点距离承印物的高度,d为承印物上剩余液膜的最小厚度,l为网线截面圆心所在垂线与表面廓线圆心所在垂线之间的距离(在本模型中其值恒为两根网线圆心距的1/2),则根据几何关系推导可得

H=d+R+cos(β+θ)R

(1)

H=R0(1-cosβ)+h

(2)

r=R0sinβ-R[1-sin(θ+β)]

(3)

l=Rsin(β+θ)+R0sinβ

(4)

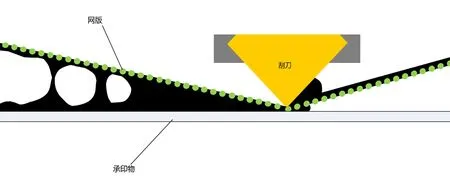
图2 Potts等用高速相机对丝网印刷过程中油墨在丝网与承印物间形成液桥的拍摄结果

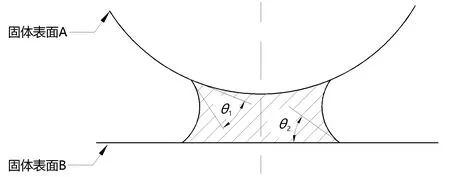
图3 Butt等提出的平面与圆柱面之间液桥的几何模型

图4 网版回弹过程中网线与承印物间形成液桥的几何模型

Butt等[6]指出,实际的上接触表面为圆柱面的液桥在演变过程中,其填充角β远小于接触角θ,且考虑到在实际的丝网印刷过程中,在液桥断裂前的一段时刻内,填充角β是一个非常小的量,则可在公式中做如下替换:将sin(θ+β)、cos(θ+β)近似为sinθ、cosθ;将sinβ近似为β;将1-cosβ近似为1/(2β2).则由式(1)、式(2)联立可得

(5)

由式(3)、式(4)可得

r=R0β-R(1-sinθ)

(6)

(7)

另外,考虑到真实回弹过程中丝网近似沿其法线方向运动且网版所在平面与承印物平面所成夹角是个小量,因此其抬升运动的水平分量可以忽略不计.设网线以匀速垂直向上运动,则网线的抬升高度h可表示为

h=vt

(8)

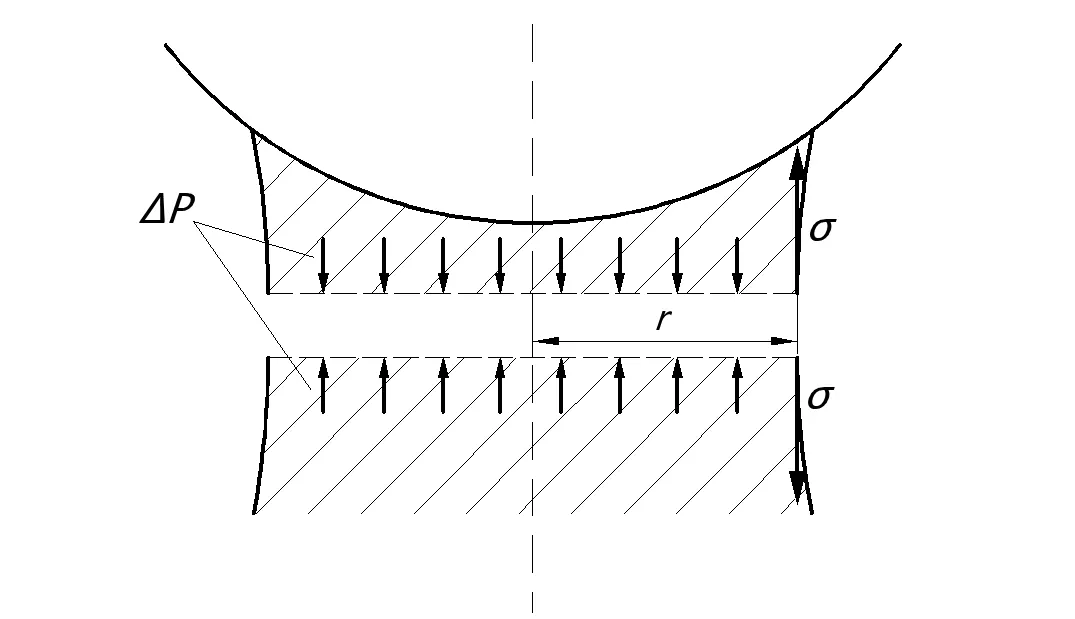
图5 液桥最小截面处表面张力与内部负压关系示意图

式(8)中,v为抬升速度,t为网线抬升时间.

如图5所示,最小截面处液桥力FL的形成原因包括两方面:一是液体的表面张力σ,二是液桥内部的负压ΔP.二者作用方向相反,相互抵消.

在液桥力的计算中,表面张力引起的分力Ft可表示为

Ft=2πσr

(9)

式(9)中,σ为油墨表面张力系数.

内部负压引起的分力Fc可表示为

Fc=ΔPπr2

(10)

式(10)中,ΔP为液桥内部负压值.

ΔP的值可由Young-Laplace方程给出并表示为

(11)

则最小截面处液桥力FL可由Ft-Fc给出并表示为

(12)

随后,令式(12)等于0并联立式(5)～式(8),便可求解出不同速度下的断裂时间,进而求得该时刻的断裂高度h、表面廓线半径R、最小截面半径r、填充角β和最小液膜厚度d.

2.2 转墨率的预测

转墨率的计算采用体积法,即利用求得的d、R、r以及其他已知的值计算出留在承印物上的油墨的体积,并通过计算其与总油墨体积的比值来计算转墨率η:

(13)

式(13)中,h0为初始时刻油墨对网线的浸没高度.

3 CFD仿真

本文用ANSYS Fluent进行网版回弹过程中液桥变化的二维CFD仿真,旨在对理论模型可靠性进行验证,模型如图6所示.

3.1 仿真条件设定

(1)网线线径为16 μm,孔径为30 μm.由于附着在网线上的液桥同样会受其他网线的影响,若想要完整呈现液桥的形态,网线的数量至少为3根.

(2)油墨设定为导电银油墨,密度为1 960 kg/m3,黏度为2 360 cP;表面张力系数为0.04 N/m,与网线之间的接触角为45 °.

(3)初始状态下网线停留在承印物上并浸没在油墨中,初始浸没高度h0为14 μm.

(4) 网线的抬升运动设为沿y轴正方向的匀速直线运动,并设置5,10,20,40 mm/s4组抬升速度.

(5)重力加速度为9.81 m/s,方向沿y轴负方向.

3.2 仿真结果分析

3.2.1 液桥演变过程 液桥的演变情况分为四个阶段.

第一阶段:网线刚开始运动时,速度较小,油墨表面会因内聚力而形成凸液面,如图7a所示.

第二阶段:网线运动速度达到最大并开始匀速运动,但仍旧被油墨浸没时,油墨不断填充着网线离开后留下的空缺位置,网线下方油墨形成负压,如图8a压力云图所示,使得凸液面逐渐转换为凹液面,如图7b所示.

第三阶段:网线继续运动,离开液面并拉伸出液桥,如图7c所示;此过程中液桥内的负压始终存在,使得液桥不断颈缩,如图8b压力云图所示.

第四阶段:网线运动到一定高度,液桥断裂,如图7d所示.

图8 仿真过程中的液桥内部压力云图(网版回弹速度为5 mm/s)

总体来看,仿真过程对液桥的演变过程进行了清晰的表征,印证了理论模型构建时液桥形态、各个几何值之间的关系及液面凸凹性的判定等多方面构想的合理性.

3.2.2 液桥力变化分析 图9展示了仿真中回弹速度为5 mm/s时的液桥在产生之初直至断裂过程中最小截面周长、面积与内部负压值随时间的变化情况,以及由上述数值所反映出的最小截面处表面张力分力、内部负压分力以及液桥力随着时间的变化情况.随着网版抬升,最小截面周长、面积均不断下降,液桥内部负压值不断上升.

在图9d中,表面张力分力值在液桥形成之初大于内部负压分力值,但二者均在不断减小且前者减小的速度要大于后者,这使得二者的差值——液桥力值不断减小直至为0.而当液桥力变为0的时间点即为仿真中液桥断裂的时刻.

图9 仿真中液桥自产生至断裂过程中最小截面周长、最小截面面积与内部负压值随时间的变化情况,以及液桥力及其两个分力随时间的变化情况(网版回弹速度为5 mm/s)

结果表明,仿真对液桥力随时间变化的情况进行了清晰表征,并对液桥演变直至断裂这一物理过程进行了具体的描述,充分证明了理论模型中对液桥力与液桥断裂时刻之间关系所作假设的合理性.

3.2.3 转墨率对比 仿真中转墨率的计算采用面积法,通过计算液桥断裂时仿真云图中转移油墨面积与油墨所占总面积的比值来近似代表转墨率,结果如表1所示.

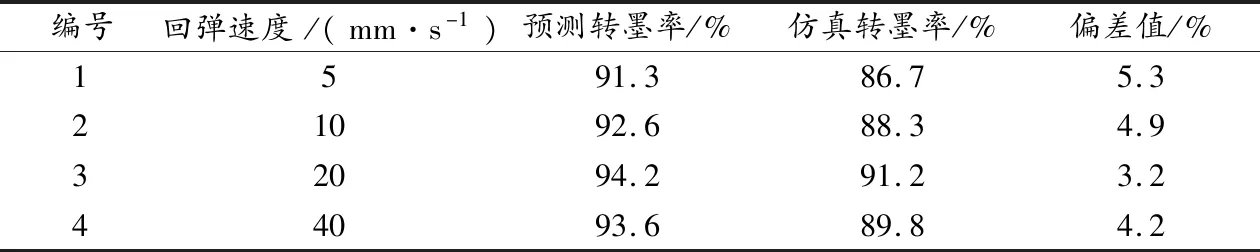
表1 不同回弹速度下转墨率的仿真结果与预测结果对比

从仿真结果来看,转墨率随着网版回弹速度的增大呈现先上升后下降的趋势,最大值出现在v=20 mm/s附近.本文模型对转墨率的预测结果较之仿真结果来说整体偏高,但偏差值不超过6%,变化趋势相近,因此预测结果可靠.

4 结语

(1)本文对丝网印刷电子转墨机理进行了深入分析,将液桥断裂的特征量引入转墨率影响因素的研究中,并基于转墨过程中网版回弹液桥演变时液桥力的变化情况,建立了一个转墨率的预测模型,为转墨率影响因素的相关研究提供了参考.

(2)用ANSYS Fluent进行了网版回弹过程中液桥变化的二维CFD仿真,对理论模型构建的合理性与结果的可靠性进行了验证,验证的偏差值不超过6%,证明了所构建理论模型的可靠性.

(3)理论模型预测是运用网版抬升速度进行计算的,而网版抬升速度还需通过刮刀速度、离网间距等实际的印刷工艺参数计算得出,因此仍需进一步的研究.