应用型本科高等数学的教学内容和引入方式探索

摘 要：高等数学一直是各学科的公共基础课，它除了可以解决各种实际问题，更是后续专业课程的基础。随着应用型本科的提出，我们将面对更多的应用型人才，高等数学的教学也应该随之改变，教学方式是重点，而教学内容的选择也非常关键。我们提出注重概念、定义的学习和理解，从定义引申出相关的性质和定理，剔除烦琐的计算和证明，而只学习基础的运算法则，学习用计算机求解，然后运用所学解决实际问题。这样，我们从不同的角度认识事物，并紧密联系现实生活，学习用理论解决实际问题，全面提高高等数学的教学质量和效果。

关键词：应用型本科；高等数学；教学内容；教学引入；基础；应用

1 概述

应用型高校一般指应用型本科院校。引导部分地方本科高校向应用型转变是党中央、国务院的重大决策部署。孔繁敏教授指出，应用型本科的人才培养模式应该为：“以知识为基础、以能力为重点，以服务为宗旨，注重知识、能力、素质的协调发展，学习、实践和职业技术能力相结合。”应用型高校人才培养目标的转变必然带来教育理念、培养方案和培养模式的深刻改革，各课程的教学也要进行相应的改革。

高等数学一直是各学科的公共基础课，它除了可以解决各种实际问题，更是后续专业课程的基础，对学生学习专业知识和培养理论创新能力起着决定性的作用。随着应用型本科的提出，很多专家学者从不同方面对高等数学的教学改革进行探索。韦娜娜、刘自强等提出将数学建模思想融入高等数学的教学过程中，以充分调动学生的学习兴趣，提高学生运用数学解决实际问题的能力。也有很多学者提出改革教学模式。吕凤姣等提出以问题为驱动的翻转课堂教学模式，充分利用优质课程资源自主探究学习。石露、张保霞等提出线上线下混合式教学模式，激发学生参与课堂教学积极性与主观能动性。叶建萍等提出微课教学革新教学理念和教学模式，以便能充分利用学生的碎片时间。邹广玉提出依托大学生数学竞赛，开展高等数学“高层次”教学的研究与实践，以促进对高等数学的教学改革和大学生数学能力的培养。杨鑫提出构建智慧课堂模型提高课堂教学效果。王帅等提议从教学目标、教学内容、思政、考核等方面进行教学改革，以提高教学质量，培养应用型的人才。

专家学者针对应用型本科的高等数学教学改革研究，大部分都集中于数学建模思想的融入和教学方式的改革，很少有人详细研究其整体教学内容的选择和引入方式。王帅等虽然也提议从教学内容进行改革，但是却没有做深入的分析。本文针对上述问题展开研究，首先分析高等数学教学中存在的一些问题，然后重点提出高等数学教学内容的选择和如何引入，最后总结我们的研究成果。

2 高等数学教学存在的问题

高等数学的地位如此重要，然而除了少数科研人员和专家学者能体会到数学所带来的好处，大部分人都无法体会它所带来的美好，以下是传统的高等数学教学中存在的一些问题。

2.1 课堂教学时间有限

虽然高等数学是基础性学科，但是在大部分的应用型本科，高等数学课程的课时并不是很多。高等数学不同于高中数学课程，具有一定的难度，在有限的教学时间内要保持高质量的教学，既是对教师能力的考验也是对学生学习态度的考验。

2.2 过于注重理论教学和计算技巧

传统的教学中，高等数学一直偏向理论教学，注重概念的讲解、原理的证明和计算技巧的练习，这些理论教学可以提高学生的逻辑思维能力和创新能力，它们对科研人员非常有用，但是对大部分应用型本科的学生而言，却无法体现它的优势。而且传统的高等数学教学忽略了原理和实际问题的结合，这与应用型本科学生注重实践能力的培养与强化这一目标不符。再者，应用型本科院校学生的基础知识掌握得不够牢固，学生的自主学习主动性不够，分析并解决问题的能力有待提高，但是他们的好奇心比较强，动手能力好。

2.3 教学模式单一，学生缺乏兴趣

在现阶段的高等数学教学过程中，主要以教师讲授为主，学生机械学习，然后适当练习。这样的教学环节束缚了学生的思维，难以引起学生的学习兴趣和学习主动性。教师在开展高等数学教学活动中，由于教师教学能力有待提升，也没有根据学生的学习情况对学生展开针对性的教学，导致学生养成了被动学习的习惯。

因此，我们需要精心挑选教学的内容，优化原有的教学模式和改进传统的教学的方式，从而提高高等数学的教学效率。

随着应用型本科的提出，我们将面对更多的应用型人才，教学方式的改进是重点，而教学内容的选择也非常关键。接下来，我们就一起来讨论应用型本科的高等数学教学内容的选择及其教学引入方式。

3 高等数学的教学内容选择和教学引入方式

根据应用型本科的培养目的，我们建议从以下五个方面选择合适的内容，并合理地引入教学。

3.1 注重概念、定义的学习和理解

3.1.1 教学内容

定义是认识一个事物的起点，研究定义和定义的起源，有助于培养学生观察、分析、总结的能力。而且对定义的学习可以加深对事物的理解，为实际应用奠定堅实的基础。所以，我们应该重点学习概念和定义。

3.1.2 教学引入

传统教学中，定义的学习方式就是直接研读，这对我们的学生来说生涩难懂，学不透彻。对于复杂的定义，有时更是粗略学习而已，这样就造成了学习的一知半解，学生即便算出结果，也不知道这是什么东西，更谈不上解决实际问题。实际上，数学与实际生活密切相关，日常生活中的种种现象无不透露着数学的奥妙。我们可以用现实的例子引入概念，通过例子归纳总结得出概念，既通俗易懂，也能激发学生学习热情。

如学习导数，可以通过物理的瞬时速度和几何的切线的斜率引入，即：瞬时速度可以看成是时间间隔很短（趋于0）时的平均速度，切线可以看成是相隔很近（趋于0）的割线的斜率，然后通过求它们趋于0时的极限即可求出这种特殊的平均速度（瞬时速度）和割线的斜率（切线的斜率），这样引导学生总结得到的这一类特殊的极限，我们称它为导数。

学习了定义之后，我们可以用定义验证中学所学的某些函数导数公式的正确性，或者用导数的定义计算一些简单函数的导数并判断可导性。如已知y=f（x）= x，用定义求解f′（x）。通过这些例题和练习对学生进行数学思维训练，加深对导数定义的理解。

綜上所述，定义是重点，我们首先要研究定义和定义的起源，并引导学生用定义来解决实际问题。

3.2 适当学习相关的性质和定理

3.2.1 教学内容

性质和定理是由定义延伸出来，反映了事物更深层次的特征，我们适当地学习相关的性质和定理，可以更全面地认识事物的本质特征。

3.2.2 教学引入

传统的性质和定理的学习都是通过证明的方式来引入的，这对于我们应用型本科的学生而言是最头疼的事情，而且用处不大。所以，我们可以引导学生通过定义引申出相关的性质和定理，不需要做严格的证明，只需要解释它们如何延伸而来即可。

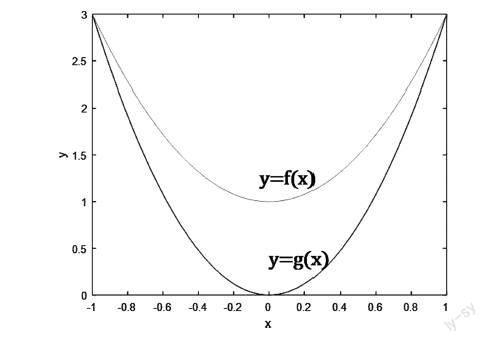
如学习定积分的性质：如果在区间［a，b］上，有f（x）≥g（x）可积，则∫baf（x）dx∫bag（x）dx。

我们可以通过定积分的几何意义曲边梯形的面积，画图来解释这个性质，如下所示：

显然，在x∈［-1，1］时，以y=f（x）为曲边的曲边梯形的面积大于以y=g（x）为曲边的曲边梯形的面积，由定积分的几何意义容易看出∫baf（x）dx∫bag（x）dx。

学习了性质之后，我们可以用性质来求解一些简单的实际问题。

如比较下列定积分值的大小：∫43lnxdx与∫43（lnx）2dx。通过这些例题和练习对学生进行数学思维训练，加深对定积分性质的理解，也加深对事物的理解，为解决实际问题做好准备。

3.3 学习基础的运算法则

3.3.1 教学内容

基础的运算法则体现了事物的基本变化规律，也是事物定义的延伸，对基础运算的学习可以加深我们对事物的认识。同时，掌握基础的运算方法才能推而广之，更快捷地求解实际问题。所以，我们应学习基础的运算法则。

3.3.2 教学引入

传统教学中，我们只是简单学习基础运算法则，而把大量的精力用于讲解复杂的求解方法，或者复杂的运算技巧。对于应用型的学生而言，这种技巧的学习用处不大。所以，我们建议剔除复杂的求解方法和运算技巧，因为复杂的计算其实是基础运算通过一定的规律复合而来，只不过需要更多的运算技巧而已。而且现代科技发达，很多复杂的计算，可以运用计算机求解，这样我们可以把更多的时间和精力用于应用。

如极限的四则运算法则，它反映了极限的基本运算规律，万变不离其宗，两个重要极限、无穷小的比较、洛必达法则等都是由四则运算法则延伸而来的。所以学习了基础的运算法则，理论上我们可以求解所有的极限，而且现实生活中，我们很少需要自己去求解复杂的极限。所以我们学习基本的运算法则，了解事物的基本变化规律，方便我们应用即可。

3.4 运用所学解决实际问题

3.4.1 教学内容

学习高等数学就是拿来应用的，否则我们就会产生质疑。说起来数学的应用无处不在，但是感觉上又虚无缥缈。带领学生一起研究它们的实际应用，可以为他们在学习高等数学上指明方向。

3.4.2 教学引入

通过学习事物的概念、性质和基础的运算方法，我们已经有了初步解决实际问题的能力，那么接下来，我们就通过相关的案例分析，引导学生用理论来解决实际问题，培养学生学以致用的能力。特别地，我们可以针对各专业，适当引入具有专业特色的案例，从而提高学生学习数学的积极性，也提高他们对自己专业的美好向往。

如学习函数和极限的应用：对于经管类的学生，我们可以先介绍我们常见的单利、复利、连续复利，学习常用的成本函数、收益函数和利润函数，通过对这些常用经济函数的学习，培养学生运用函数和极限解决经济问题的能力。对于工程类或者环境类的学生而言，我们可以引入下面这类例子：空气通过盛有CO2吸收剂的圆柱形器皿，已知它吸收CO2的量与CO2的百分浓度及吸收层厚度成正比，今有CO2含量为8%的空气，通过厚度为10厘米的吸收层后，其CO2含量为2%，问：（1）若通过的吸收层厚度为30cm，出口处空气中CO2的含量是多少？（2）若要使出口处的空气中CO2的含量为1%，其吸收层的厚度应多少？

通过实际的案例分析，将理论应用到实际问题，可以激发学生学习的热情，体验数学的无穷魅力。

3.5 引入Matlab实验

3.5.1 教学内容

我们现在处于高速发展的信息化时代，其基本特征就是计算机的高速发展，用计算机来求解数学问题已是常态。因此，我们可以把复杂的计算交给计算机，把更多的精力放在实际应用中。因此，我们引入Matlab实验，用来求解高等数学中较为复杂的运算。

3.5.2 教学引入

首先介绍Matlab这个强大的求解数学问题的软件，然后讲解数学中最基本的函数如何用计算机语言来描述，接下来依次介绍基本的绘图和其他数学运算命令，如求解极限、导数、积分、微分方程等。

如，求解极限

2－x3－xx。常规计算，我们需要凑成第二重要极限来求解，求解过程烦琐，也需要一定的计算技巧和时间。然而，用Matlab求解的话，只需要输入以下命令即可：

limit（（（2-x）/（3-x）^x，inf）

通过Matlab实验，让学生学会用计算机求解复杂的计算题，应用起来更方便，而且学习用Matlab软件，可以跟紧时代步伐，激发学生学习的热情，体会科技的强大和它们所带来的便利。

综上所述，对于应用型本科的高等数学教学而言，我们应该精心挑选合适的教学内容，组织合适的教学引入方式，再充分利用各种信息化技术，革新我们的教学模式，这样既能提高学生的学习兴趣，培养学生的自主学习能力和自主学习意识，也能充分利用学生的碎片时间，从而全面提高高等数学的教学质量和效率。

结语

随着应用型本科的提出，我们将面对更多的应用型人才，其人才培养注重：“以知识为基础、以能力为重点，以服务为宗旨，注重知识、能力、素质的协调发展，学习、实践和职业技术能力相结合。”因此，对于有着重要地位的高等数学，我们的教学策略也应该随之改变，教学方式是重点，而教学内容的选择也非常关键。我们提出注重概念、定义的学习和理解，从定义引申出性质和定理，剔除烦琐的计算和证明，而只学习基础的运算法则，学习用计算机求解，然后运用所学解决实际问题。这样，我们从不同的角度认识事物，并用理论解决实际问题，学以致用，全面提高高等数学的教学质量和效果。

参考文献：

［1］王帅，陈修梅.应用型本科高校高等数学的教学改革探索［J］.大学，2021（19）：2124.

［2］袁伯园，林大志，王茜.应用型本科高等数学教学改革的初步研究——结合俄罗斯高等数学教学模式［J］.教育教学论坛，2020（39）：217218.

［3］王明芬.浅谈转型期应用型高校高等数学的教学改革［J］.吉林工商学院学报，2020，36（05）：124125.

［4］张保霞.应用型本科院校高等数学线上线下混合式教学模式的探讨［J］.科技视界，2021（14）：109110.

课题项目：广西农业职业技术大学2022年教育教学研究课题，“三教”改革背景下的职业本科《高等数学》实践教学的改革与探究（项目编号：YJ2208）

作者简介：陶艳蓉（1982— ），女，广西桂林人，硕士，讲师，研究方向：高等数学。