高二下学期期末复习卷（B卷）答案与提示

一、选择题

1.C

3.B 提示:不妨设1≤x10。

所以a≥(1-lnx)max。

因为y=1-lnx在区间[1,e]上单调递减,所以(1-lnx)max=1-ln 1=1,故a≥1。

4.A

5.D 提示:已知(2x-3)5=a0+a1(x-1)+a2(x-1)2+a3(x-1)3+a4(x-1)4+a5(x-1)5。

令x=0,整理可得-243=a0-a1+a2-a3+a4-a5。①

令x= 2,整理可得1=a0+a1+a2+a3+a4+a5。②

由①+②得,-242=2a0+2a2+2a4,所以a0+a2+a4=-121。

其中恰有2 只兔子相邻走出笼子方案为:先排5只鸡,会产生6个空隙,再从3 只兔子中选2 只捆绑排列,最后与剩下的兔子排列到6个空隙中共有种方案。

7.B 提示:f(x)=ex-mx+n-1,则f′(x)=ex-m。

①当m≤0 时,f′(x)>0 恒 成 立,则f(x)单调递增。而f(0)=n,显然f(x)≥0不恒成立。

②当m>0 时,当x∈(-∞,lnm)时,f′(x)<0,函 数f(x)单 调 递 减;当x∈(lnm,+∞)时,f′(x)>0,函数f(x)单调递增。

故f(x)min=f(lnm)=m-mlnm+n-1。

因f(x)≥0 恒成立,故m-mlnm+n-1≥0,即n≥mlnm-m+1。

故h(m)min=h(1)=0。

8.D 提示:因为f(x)为奇函数,所以f(-x)=-f(x)。

当x>0 时,xf′(x)<2f(-x)=-2f(x)⇔2f(x)+xf′(x)<0。

又g(x)=x2f(x),则g′(x)=2xf(x)+x2f′(x)=x[2f(x)+xf′(x)]。

当x>0时,g′(x)<0,g(x)在区间(0,+∞)上单调递减。

当x∈R 时,g(-x)=(-x)2·f(-x)=-x2f(x)=-g(x),故g(x)=x2f(x)为R 上的奇函数。

又f(x)在R 上的图像连续不断,故g(x)在R 上单调递减。

又因为g(log2(x2-2))+g(-1)>0,所以g(log2(x2-2))-g(1)>0,即g(log2(x2-2))>g(1)。

当x∈[1,+∞)时,f′(x)=ex-1--a单调递增,故f′(x)min=f′(1)=-a。

①若a≤0,则f′(x)≥0,所以f(x)在x∈[1,+∞)上单调递增,f(x)≥f(1)=1恒成立。

②若a>0,则f′(1)= -a<0,由f′(x)单调递增知,存在x0>1,使得f′(x0)=0。

当x∈[1,x0)时,f′(x)<0,f(x)单调递减;当x∈(x0,+∞)时,f′(x)>0。

所以f(x0)1使得f(x0)<1,a>0不满足题意。

综上,a≤0。

二、填空题

于是可得,当a≤1时,方程2x2-x-a=0在x∈(1,+∞)上无解,即f′(x)>0恒成立,f(x)在(1,+∞)上单调递增。

又f(1)=0,所以方程x2-alnx-x=0在区间(1,+∞)上无零点,不符合题意。

综上,实数a的取值范围为(1,+∞)。

14.120 提示:由题意分两种情况:

故x2的系数为108+12=120。

15.0.000 25 提示:记“患肺癌”为事件C,“吸烟”为事件A。

由题意得P(C)=0.001,P(A)=0.20,P(C|A)=0.004。

由全概率公式得,P(C)=P(C|A)·P(A)+P(C|)P()。

将数据代入,得0.001=0.004×0.20+P(C|)×0.80,解得P(C|)=0.000 25。

则f(x)=(ex+c)ex。

因为f(0)=2,即1+c=2,所以c=1,f(x)=(ex+1)ex=e2x+ex。

又因为x(f(x)-a)≥1+lnx+xex恒成立,所以x(e2x-a)≥1+lnx。

理由如下:构造φ(x)=ex-x-1,则φ′(x)=ex-1。令φ′(x)=0,得x=0。若x>0,则φ′(x)>0;若x<0,则φ′(x)<0。故φ(x)在x=0处取得极小值,也是最小值,φ(x)≥φ(0)=0,从而得证。

三、解答题

曲线y=f(x)在点(0,f(0))处的切线斜率k切=f′(0)=2。

又f(0)=-1,则切点为(0,-1)。

所求切线方程为y-(-1)=2(x-0),即2x-y-1=0。

又ex>0,由f′(x)=0,得x=-1 或x=2。

当x∈(- ∞,-1)和(2,+ ∞)时,f′(x)<0,此时f(x)单调递减;

当x∈(-1,2)时,f′(x)>0,此时f(x)单调递增。

18.(1)设“第一次检测出的是次品且第二次检测出的是正品”为事件A,则P(A)=。

(2)X的可能取值为200,300,400,则

故X的分布列如表1所示。

表1

19.(1)设A表示“螺钉是次品”,B1表示“螺钉由Ⅰ号机器生产”,B2表示“螺钉由Ⅱ号机器生产”,B3表示“螺钉由Ⅲ号机器生产”,则P(B1)=0.35,P(B2)=0.4,P(B3)=0.25。

20.(1) 由题意得,(0.006+a+0.018+0.032+0.02+0.01)×10=1,解得a=0.014。

(2)设全校学生成绩的第80百分位数为t。

因为0.1<0.2,0.1+0.2>0.2,所以t∈[80,90),0.1+(90-t)×0.02=0.2,则t=85。

估计全校学生成绩的第80 百分位数为85。

(3)因为成绩在[80,90)与[90,100]的学生比例为2∶1,所以从全校成绩在80分及以上的学生中抽取1 人,此人成绩在[90,100]的概率为。

X的分布列如表2所示。

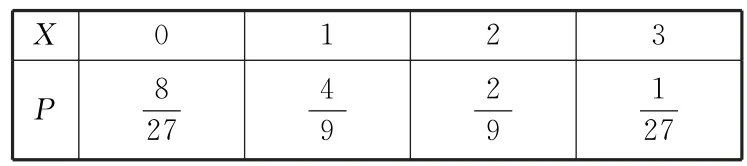
表2

21. (1)(i)分别设抽取的客户为青年人、中年人、老年人为A1、A2、A3,抽到男性为事件B。

由已知可得,P(A1)=0.15,P(A2)=0.5,P(A3)=0.35,P(B|A1)=0.2,P(B|A2)=0.35,P(B|A3)=0.55。

由已知可得,抽取的客户是男性的概率为P(B)=P(A1)·P(B|A1)+P(A2)·P(B|A2)+P(A3)·P(B|A3)=0.15×0.2+0.5×0.35+0.35×0.55=0. 397 5。

两个变量有很强的线性相关性。

22.(1)F′(x)=(x+1)ex-3a(x+1)·(x-1)=(x+1)(ex-3ax+3a)。

令g(x)=ex-3ax+3a,则g′(x)=ex-3a。令g′(x)=0,解得x=ln 3a。

当x∈(-∞,ln 3a)时,g′(x)<0;当x∈(ln 3a,+∞)时,g′(x)>0。

所以g(x)在(-∞,ln 3a)上单调递减,在(ln 3a,+∞)上单调递增。

g(x)min=g(ln 3a)=6a-3aln 3a=3a(2-ln 3a)。

因为x=-1 是函数F(x)=xex-a(x3-3x)的唯一极值点,且a>0,所以g(ln 3a)≥0,即当时,g(x)≥0恒成立。

当x∈(-∞,-1)时,F′(x)<0,F(x)在(-∞,-1)上单调递减;

当x∈(-1,+∞)时,F′(x)>0,F(x)在(-1,+∞)上单调递增。

故F(x)有且仅有一个极值点x=-1。

所以正实数a的取值范围为。

(2)G(x)=f(x)-m(x+lnx)=xexmln (xex)(m>0)的定义域为(0,+∞)。

令t=xex>0,则上述函数变形为h(t)=t-mlnt。

对于t(x)=xex,x∈(0,+∞),则t′(x)=(1+x)ex>0,即t(x)=xex(0,+∞)上单调递增。

已知存在实数x1,x2使得G(x1)=G(x2),不妨设x1

因为m>0,所以当0m时,h′(t)>0,h(t)在(m,+∞)上单调递增。

所以t=m为函数h(t)的唯一极小值点。0m。

令φ(t)=h(t)-h(2m-t)。

又h(t1)=h(t2),所以h(t2)>h(2mt1)。

由h(t)的单调性可知t2>2m-t1,即有t2+t1>2m成立,所以。