高考中概率典型例题赏析
■河南省郑州第一〇一中学 冯连福
数学建模是指对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型来解决问题的过程。高考数学对数学建模这一核心素养进行考查的形式主要体现在概率与统计试题。《中国高考报告(2023)》再次强调数学概率与统计试题将会以复杂情景的形式呈现,信息识别与加工会更加明显。下面我们将概率中典型例题进行一一分析,同学们要学会收集信息→加工信息→数学建模→运算求解→解决问题;举一反三,提高自己科学探究与思维建模、逻辑推理能力。
类型一、两点分布
例1某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响。已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积。
(1)记“函数f(x)=x3+ξ为R 上的奇函数”为事件A,求事件A的概率;
(2)求ξ的概率分布和数学期望。
分析:(1)由于函数f(x)为奇函数,则ξ=0,表示该学生选修三门功课或三门功课都没选,可求事件A的概率;(2)由已知可得ξ=0或2,则ξ的分布列可求。
解:设该学生选修甲、乙、丙的概率分别为x、y、z。
(1)若函数f(x)=x3+ξ为R 上的奇函数,则ξ=0。
当ξ=0时,表示该学生选修三门功课或三门功课都没选。
故P(A)=P(ξ=0)=xyz+(1-x)(1-y)(1-z)=0.4×0.5×0.6+(1-0.4)×(1-0.5)×(1-0.6)=0.24。
事件A的概率为0.24。
(2)依题意知ξ=0或2,则ξ的概率分布如表1所示。

表1
因此,ξ的数学期望为E(ξ)=0×0.24+2×0.76=1.52。
类型二、超几何分布
例2已知10件不同的产品中共有3件次品,现对它们进行一一测试,直到找出所有3件次品为止。
(1)求恰好在第5 次测试时3 件次品全部被测出的概率;
(2)记恰好在第k次测试时3 件次品全部被测出的概率为f(k),求f(k)的最大值和最小值。
分析:(1)恰好在第5次测试时次品全部被测出,则第5次取次品,前4次中取2件次品、2件正品;(2)恰好在第k次测试时次品全部被测出需分类讨论。
(2)根据题意,分析可得k的范围是3≤k≤9。
当3≤k≤6时,若恰好在第k次测试时3件次品全部被测出,则第k次取出第3 件次品,前k-1次中有2次是次品,k-3次是正品。而从10 件产品中顺序取出k件,有种情况。
当k=7时,即恰好在第7次测试时3件次品全部被测出,有两种情况,一是第7次取出第3件次品,前6次中有2次是次品,4次是正品;二是前7次没有取出次品,此时也可以测出三件次品。
当k=8时,即恰好在第8次测试时3件次品全部被测出,有两种情况,一是第8次取出第3件次品,前7次中有2次是次品,5次是正品;二是前7次恰有一次次品,第8次取出为合格品。
类型三、二项分布
例3我国的5G 研发在世界处于领先地位,到2022年底已开通5G 基站超过231 万个,占全球比例超过60%。某科技公司为基站使用的某种装置生产电子元件,该装置由元件A和元件B按如图1的方式连接而成。已知元件A至少有一个正常工作,且元件B正常工作,则该装置正常工作。据统计,元件A和元件B正常工作超过10 000小时的概率分别为。

图1
(1)求该装置正常工作超过10 000小时的概率;
(2)某城市5G 基站建设需购进1 200台该装置,估计该批装置能正常工作超过10 000小时的件数。
分析:(1)三个元件A为并联,再与元件B串联,进而求出该装置正常工作超过10 000小时的概率;(2)该批装置服从二项分布,故可以估计出该批装置能正常工作超过10 000小时的件数。
类型四、正态分布
例 4“过大年,吃水饺”是我国不少地方过春节的一大习俗。2023 年春节前夕,A市某质检部门随机抽取了100包某种品牌的速冻水饺作样本,检测其某项质量指标,检测结果的频率分布直方图,如图2所示。
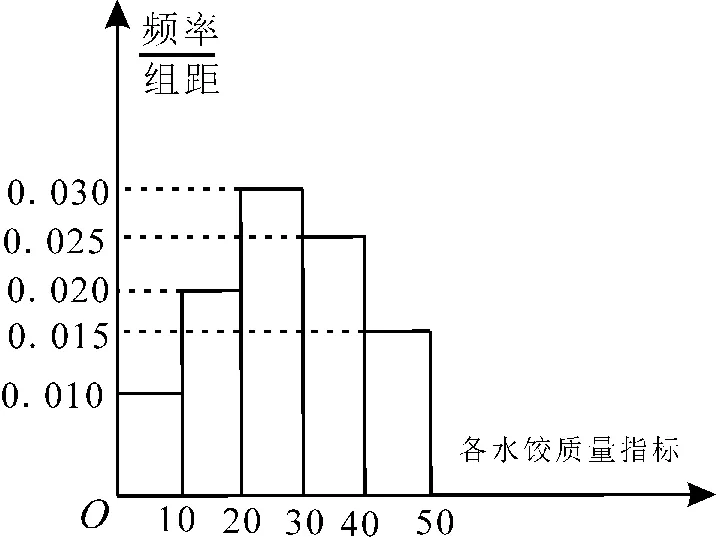
图2
(1)求所抽取的100 包速冻水饺该项质量指标值的样本平均数和方差s2(同一组中的数据用该组区间的中点值作代表)。
(2)若该品牌的速冻水饺的某项质量指标Z服从正态分布N(u,σ2),其中u近似为样本平均数,σ2近似为样本方差s2。
①求Z落在(14.55,50.40)内的概率;
② 若某人从某超市购买了1 包这种品牌的速冻水饺,发现该包速冻水饺某项质量指标值为55,根据3σ原则判断该包速冻水饺某项质量指标值是否正常。
②若Z~N(u,σ2),则P(u-σ 解:(1)所抽取的100包速冻水饺该项质量指标值的样本平均数 ̄x=5×0.1+15×0.2+25×0.3+35×0.25+45×0.15=26.5。 方差s2=(-21.5)2×0.1+(-11.5)2×0.2+(-1.5)2×0.3+(8.5)2×0.25 +(18.5)2×0.15≈142.75。 根据3σ原则判断该包速冻水饺某项质量指标值是正常的。 例5某公司准备将1 000 万元资金投入到市环保工程建设中,现有甲、乙两个建设项目供选择,若投资甲项目一年后可获得的利润为ξ1(万元)的概率分布列如表2所示。 表2 且ξ1的期望E(ξ1)=120。 若投资乙项目一年后可获得的利润ξ2(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否受第二和第三季度进行产品的价格调整,两次调整相互独立,且调整的概率分别为p(0 表3 (1)求m,n的值; (2)求ξ2的分布列; (3)根据投资回报率的大小请你为公司决策:当p在什么范围时选择投资乙项目,并预测投资乙项目的最大投资回报率是多少。(投资回报率=年均利润/投资总额×100%) 分析:(1)由E(ξ1)=120和m+0.4+n=1 求出m,n;(2)先由ξ2的可能取值为41.2,117.6,204.0,求出每一个的概率;(3)投资回报率最大即为期望最大。 解:(1)由题意得: 解得m=0.5,n=0.1。 (2)ξ2的可能取值为41.2,117.6,204.0。 P(ξ2=41.2)=(1-p)[1-(1-p)]=p(1-p); P(ξ2=117.6)=p[1-(1-p)]+(1-p)(1-p)=p2+(1-p)2; P(ξ2=204.0)=p(1-p)。 所以ξ2的分布列如表4所示。 表4 (3)由(2)可得: 根据投资回报率的计算办法,如果选择投资乙项目,只需E(ξ1) 即120<-10p2+10p+117.6,解得0.4 因为E(ξ2)=-10p2+10p+117.6,所以当时,E(ξ2)取到最大值为120.1,即预测投资回报率的最大值为12.01%。 例6某芯片代加工工厂生产某型号芯片每盒12片,每批生产若干盒,每片成本1元,每盒芯片需检验合格后方可出厂。检验方案是从每盒芯片随机取3 片检验,若发现次品,就要把全盒12 片产品全部检验,然后用合格品替换掉不合格品,方可出厂;若无次品,则认定该盒芯片合格,不再检验,可出厂。 (1)若某盒芯片中有9片合格,3片不合格,求该盒芯片经一次检验即可出厂的概率。 (2)若每片芯片售价10 元,每片芯片检验费用1元,次品到达组装工厂被发现后,每片需由代工厂退赔10元,并补偿1片经检验合格的芯片给组装厂。设每片芯片不合格的概率为p(0 ①若某盒12 片芯片中恰有3 片次品的概率为f(p),求f(p)的最大值点p0; ②若以①中的p0作为p的值,由于质检员操作疏忽,有一盒芯片未经检验就被贴上合格标签出厂到组装工厂,试确定这盒芯片最终利润X(单位:元)的期望。 分析:(1)该盒芯片经一次检验即可出厂即取3片检验都是正品,为二项分布;(2)先求出f(p),再用基本不等式或导数求出最大值;(3)X服从二项分布。 则E(X)=120-12-30-3×2=72。 这盒芯片最终利润X的期望是72元。 例7世界杯足球赛淘汰赛阶段的比赛规则为:90 min 内进球多的球队取胜,如果参赛双方在90 min内无法决出胜负(踢成平局),将进行30 min的加时赛,若加时赛阶段两队仍未分出胜负,则进入“点球大战”。点球大战的规则如下:①两队各派五名队员,双方轮流踢点球,累计进球个数多者胜;②如果再踢满五球前,一队进球数已多于另一队可能踢中的球数,则该队胜出,譬如:第四轮结束时,双方进球数为2∶0,则不需踢第5轮了;③若前五轮点球大战中,双方进球数持平,则采用“突然死亡法”决出胜负,即从第6轮起,双方每轮各派一人踢点球,若均进球或均不进球,则继续下一轮。直到出现一队进球另一队不进球的情况,进球方胜。 现有甲乙两队在淘汰赛中相遇,双方势均力敌, 120 min(含加时赛)仍未分出胜负,须采用“点球大战”决定胜负。设甲队每名球员射进的概率为,乙队每名球员射进的概率为。每轮点球结果互不影响。 (1)设甲队踢了5球,X为射进点球的个数,求X的分布列与期望; (2)若每轮点球都由甲队先踢,求在第四轮点球结束时,乙队进了四个球并刚好胜出的概率。 分析:(1)先分析出X服从二项分布,进而写出分布列;(2)由点球大战的规则分析出甲乙两队四轮比分为2∶4为关键之处。 所以X的分布列如表5所示。 表5 (2)设“第四轮点球结束时,乙队进了4个球并胜出”为事件A。 法一:由题意知,“甲乙两队前三轮比分为1∶3且第四轮甲队进球”为事件A1。 “甲乙两队前三轮比分为2∶3且第四轮甲队不进球”为事件A2。 法二:则甲乙两队四轮比分为2∶4。 例8某学校要对学生进行身体素质全面测试,对每位学生都要进行9选3 考核(即共9 项测试,随机选取3 项),若全部合格,则颁发合格证;若不合格,则重新参加下期的9选3 考核,直至合格为止。若学生小李抽到“引体向上”一项,则第一次参加考试合格的概率为,第二次参加考试合格的概率为,第三次参加考试合格的概率为,若第四次抽到可要求调换项目,其他选项小李均可一次性通过。 (1)求小李第一次考试即通过的概率P; (2)求小李参加考核的次数ξ分布列。 分析:(1)小李能够通过考试的概率取决于是否能够抽到“引体向上”这个项目,如果没有抽到,则必能通过;若抽到“引体向上”则通过的概率为。后面通过测试的概率受到前面抽签的影响,要利用条件概率进行解决。(2)显然ξ=1,2,3,4,在参加下一次考核时,意味着前几次考核失败,所以当ξ取2,3,4时,要考虑前面考核失败的情况与该次考核成功两个方面同时成立。 故ξ的分布列如表6所示。 表6 例9为激发学生加强体育活动,保证学生健康成长,某校开展了校级排球比赛,现有甲乙两人进行比赛,约定每局胜者得1分,负者得0 分,比赛进行到有一人比对方多2 分或打满8 局时停止。设甲在每局中获胜的概率为,且各局胜负相互独立。已知第二局比赛结束时比赛停止的概率为。 (1)求p的值; (2)设X表示比赛停止时已比赛的局数,求随机变量X的分布列和数学期望E(X)。 解:(1)依题意,当甲连胜2局或乙连胜2局时,第二局比赛结束时比赛停止。 (2)依题意知,X的所有可能值为2,4,6,8。 所以随机变量X的分布列如表7所示。 表7类型五、决策问题


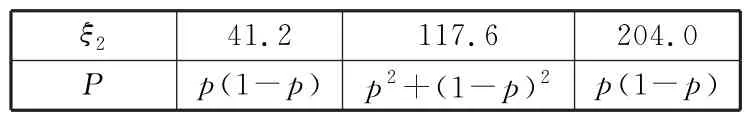
类型六、概率最值问题
类型七、比赛问题

类型八、条件概率型



