以点为“核” 在比对中感知图像的意义——《正比例的图像》教学及思考

文|年红梅

【教学内容】

苏教版六年级下册第六单元。

【教学过程】

一、复习旧知

师：还记得什么是正比例吗？

生：两个量相除，如果除的结果是一个定值，这两个量就成正比例关系。

生：成正比例的两个量，它们的比值是一定的。

生：两种相关联的量，如果比值一定，这两种量就成正比例关系。

【反思：回顾旧知，让学生再次感受两种相关联的量需具备怎样的条件才能构成正比例关系，为学生从图像中感知两种相关联量之间变化关系做好铺垫。】

二、借助直觉，猜想验证

1.借助数学直观进行猜想

师：仔细观察表格中两个量的变化成什么关系？

生：成正比例关系。

师：你知道图1中横轴和纵轴各表示什么吗？

图1

生：横轴表示汽车行驶了多少小时，是时间；纵轴表示汽车行驶了多少千米，是路程。

师：在这张方格图中，哪个点能表示出这辆汽车行驶1 小时与行驶80 千米路程的对应点？

生：先找出经过1 小时对应的直线，再找出经过80 千米对应的直线，两条直线的交点就是1小时行驶80 千米对应的点。

师：第一步先在横轴上找出1小时的点；第二步，过这个点画与纵轴平行的直线；第三步，在纵轴上找出80 千米的点；第四步，再过这个点画与横轴平行的直线。这样，两次画的直线的交点就是1小时行驶80 千米对应的点。

师：表格中的信息可以用下图中的点表示。（图2）

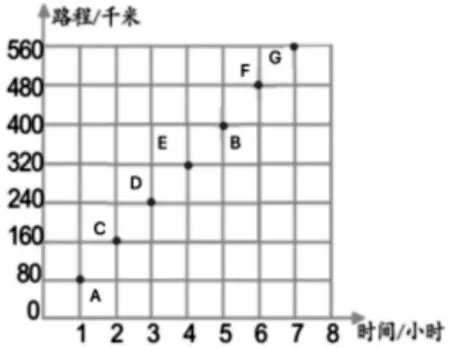
图2

师：这张方格图中，B 点表示这辆汽车行驶了多少小时？此时行了多少千米？

生：5 小时，行驶400 千米。

师：其他各点呢？想一想，与同伴交流一下。

（学生回答略）

师：方格图中的这些点的变化趋势是怎样的？拿出你的手，把它的变化趋势比划一下。

师：同学们表示的很对，随着时间的增加，路程也在不断增加。

【反思：之所以把教材例2 中标好的带点的方格图改为直接呈现图1不带点方格图，出发点是想让学生根据表格中两个相关联的量体会两个量之间的对应关系，从而经历把这种对应关系用点表示出来的过程。让学生用手势来表示这几组数据的变化趋势，意在让学生初步整体感受正比例图像的特征。整个环节学生参与度高，学习兴趣浓厚。通过由“形”到“数”的逆向思考，可以强化学生对数形结合的数学思想的感悟，同时再次体会两种相关联的量之间的对应关系，即比值一定。】

2.描点连线，验证猜想

师：请同学们在《作业单》中的方格图中（图1），描出例题表格中各组数据对应的点并按照顺序连接起来。

反馈：呈现几个连点成线时线连接的不够“平滑”的作品。交流在连点成线时要注意的事情。

师：连接图中各点，你有什么发现？

生：把这些点连接起来，就成为一条直直的线。

生：我们还可以看出正比例图像是一条直线。

师：在这条直线上任意一点都能找出一组对应的数值吗？

小结：在这条直线上任意取一点，都能找出一组对应的数值。反之，一组对应的数值，也只能找出一个对应点。

师：（出示图3，张强连接的图像）请同学再次观察，这些线是怎样形成的？

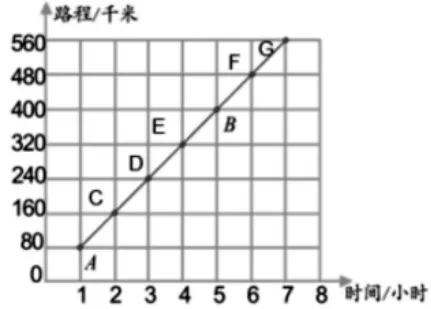
图3

生：先找点，再把这些点用平滑线连接起来。

师：也就是说，这些点都在同一条直线上，直线上任意一点都能直观地看出汽车行车的时间，同时也能看出这辆汽车行车的路程，更能反映这辆汽车行驶的时间和路程之间的变化关系。

师：李铭连接的图像是这样的（图4）。仔细观察与张强连接的图像有什么不同？

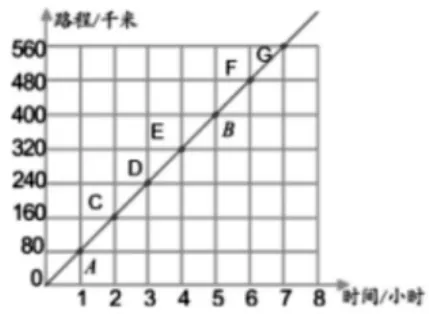
图4

生：张强是根据表格中给出的数据连接的。所以，没有从0 点开始连接。

生：表格里没有出现0 小时和8 小时，所以我们都没有从0 点开始连接。也没有多“伸出去”一点。

师：你们觉得哪种连接好呢？

生：李铭连接得好。李铭连接的图像不但能看出1 小时之前汽车行驶的路程，还能看出汽车7小时之后行驶的路程。

师：李铭的图像虽然能看出1小时之前行驶的路程和7 小时之后行驶的路程，但表格中没有给出数据呀！

师：同学们想一想，这辆汽车在运行时，需要不需要从零点几小时开始运行？你再看表格中上下两个省略号表示什么意思？由此你又有什么想说的？

生：李铭同学连接的图更能说明表格中两个省略号所表示的意思，两者相比我们发现，李铭的图像更合理、更接近事实。

【反思：通过找一找、画一画、连一连的操作活动，让学生动手直观感知并验证正比例图像的特点：两个相关联的量中，一个量变化，另一个量也随着变化，但是在变化中存在不变———每组数据的比值一定，深度理解正比例图像隐藏的变化规律。同时，考虑到学生按照教材表格中的数据来描点、连线，连出来的正比例图像不会从0 点开始，而教材练习题中给出的正比例图像则有从0 点开始连接的，基于发展性教学考虑，笔者通过两种描点、连线的方法，通过比一比、说一说，让学生感受两种不同的连线结果之间存在的区别，结合实际，内化哪一种图像更能描述汽车整个行驶的过程，并从中感受数学与生活之间联系。】

三、看图判断，学会推理

师：你能不看表格，根据图像直接判断这辆汽车3.5 小时行驶多少千米吗？

生：3.5 小时在横轴上3 和4之间，3.5 小时往上画垂线与这条斜线相交的点，在纵轴上的对应位置应当在240 和320 中间，也就是280 千米。

师：这仅仅是我们的推测，让我们一起画图验证。

（课件动态演示）

师：让我们用同样的方法试着找一找行驶520 千米需要多少小时？

生：520 千米在纵轴上480 和560 中间，图像上对应的点在横轴上的位置应当在6 和7 中间，是6.5 小时。

小结：线是由点构成的，从点的变化可以看出汽车行驶的路程在变化，汽车行驶的时间也在发生变化。随着时间的增加，行驶的路程也越来越多，点的位置也越来越高。反之，时间越短，行驶的路程也就越少，点的位置就越来越低。不管时间和路程怎么变，这辆汽车的速度是不变的。

【反思：教师提出：“你能不看表格，根据图像直接判断这辆汽车3.5 小时行驶多少千米？”的问题，意在让学生运用推理的方法，直接找出3.5 小时汽车行驶的路程。让学生在方格图上，用“作图的方法”，画出3.5 小时与图像的交点，意在验证前面的推理，为今后学习函数及函数图像打下一定基础。“用这样的方法在直线上任意找出几个点，说说它们表示的意义”，意在引领学生经历从直观地看到凭空地想、最后实现抽象和建模的过程。这样从静态地看和想到动态地画和连，从离散的点到连续的点，从有限的线段长到无限的直线，将抽象的路程、速度、时间这一数量关系与几何直观对接起来，实现了抽象思维与形象思维的结合，使正比例图像的本质逐渐变得看得见、看得清、看得远。让学生深深体会到图像中蕴含着数量关系式。】

四、课堂小结（略）