研读新课标存在的主要问题与解决策略

文|周晓林

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）颁布近一年，数学教师在这一年里经历了多次的培训，聆听了很多课标研制专家和研究学者的专题讲座，研读了新课标的文本。应该说，对于新课标的理念和变化有了一定的了解，但是对于如何读课标，如何用课标，如何基于课标实施教学还有很多的困惑。

一、小学数学教师课标研读存在的主要问题

通过课堂观察和教师访谈，笔者发现这些困惑产生的原因主要有以下几点：

（一）缺乏课标研读的整体视角

整体视角就是能用大视角对教材中具有某种内在关联性的内容进行分析、重组、整合，从整体上把握学业内容的源与流，进而从源到流进行统整，构建具有某种内在关联性的大单元。

但大多教师在研读新课标时往往只关注局部的教学内容，缺乏对课标的整体把握。比如《认识周长》一课，教师们会认真研读新课标中关于周长的要求和描述，了解内容要求、学业要求和教学提示。但因缺乏整体视角，常会有如下困惑：为什么要将三条边画到一条直线上？是基于实例的需要还是规定的操作？如何引导学生感受把边线画到一条直线上的必要性？如何体会边线的价值？如何从边线的长度体会线段长度的可加性？

类似困惑的产生就是因为缺乏课标研读的整体视角，有了整体视角就会有对课标要求的系统性理解，就能整体把握新课标的变化，厘清内在的逻辑关系。

（二）缺乏课标研读的细节研磨

细节研磨需要从新课标的描述中寻找关键词，对文本进行细节解读，在细节解读中理解和应用新课标，将新课标的要求落实到具体的课堂实践。

但是许多教师往往没有这样的意识，只是把新课标当作一种理论和说法，没有很好地进行细节研磨，从中寻找实践做法的指导。比如研读新课标关于“用数对确定位置”的描述，有教师会困惑：怎么体会有序？数对是如何出现的？怎么体会数对与点的对应？如何引导学生理解坐标的意义？怎样让学生从数去感受形、从数对的变化去感受图形的运动？要解决困惑，落实新课标的要求，就需要我们寻找其中的关键词，对“数对”“有序数对”“点”“对应”的含义进行深入琢磨。

教师只有对新课标的文本进行细节研磨，通过仔细琢磨新课标的要求，从中寻找行动的方向和实践的力量，才能深入理解新课标要求的具体含义，才能依据课标实施教学。

（三）缺乏课标研读的系统把握

系统把握就是对学习内容一致性的理解和把握，能够深度理解学习内容内在结构的一致性，体会算理理解或算法把握的一致性，形成对一类学习内容的结构化理解和深度思考。

比如对于运算一致性的研究，特别是关于整数、小数、分数运算一致性的研究已经有了很多成果。但是多位数的乘法之间有一致性吗？如何体会多位数乘一位数和两位数乘两位数之间的内在一致性？如何让学生“感悟从已知到未知的转化”？整数乘法的未知如何向已知转化？这些问题是教师在实践中很容易产生的困惑。

要解开这些困惑，就需要教师把握内容之间内在结构的一致，理解知识发生发展的来龙去脉，认真领会和感悟课标中强调的一致性。通过梳理终始根结，引导学生构建具有一致性的认知结构。

二、小学数学教师课标研读的视角与策略

新课标不仅仅是一种说法，它更应该是一种做法，是指导教师进行数学课堂教学的做法，我们应当基于产生困惑的主要原因，用实践破解课标研读的困惑。

（一）要以大视角构建对课标的整体理解

课标研读要有大视角，要用整体观和系统论发现不同学段内容之间的内在关联，从整体上把握学业内容的脉络，通过统整相关内容构建具有某种内在关联性的大单元，整体把握新课标内在的逻辑关系，形成对课标的系统性理解。例如教学“认识周长”这一内容，我们就应基于整体视角研读课标，构建对学习内容的系统理解和把握。

1.用整体视角寻找理解周长概念的关键问题

新课标中关于“认识周长”的描述主要有内容要求、学业要求和教学提示。内容要求强调的是“结合实例”；学业要求强调的是“经历用直尺和圆规将三角形的三条边画到一条直线上的过程，直观感受三角形的周长，知道什么是图形的周长”；教学提示强调的是“可以借助用直尺和圆规作图的方法，引导学生自主探索三角形的周长，感知线段长度的可加性”。

我们特别要注意学业要求的描述“直观感受三角形的周长，知道什么是图形的周长”和教学提示中的要求“感知线段长度的可加性”。通过将三角形的三条边画到一条直线上的数学活动，学生能直观感受到三角形的周长就是由它的三条边组成的总长度，由此迁移到对什么是图形的周长的认识。也就是说，对于认识周长课标给出了一个研究路径：

为什么要把三条边画在一条直线上？这与实例有关，与线段有关，和新课标在“线的认识”时特意强调的“通过面的边缘认识线段”有关。正因为三条边就是三角形面的边缘线，它们组合在一起的线段恰好是三角形一周边线的长度。所以把三角形三条边画到一条直线上的活动就是体会三角形一周边线的长度的活动，就是揭示周长概念本质的活动。

通过课标研读，我们能从整体上构建周长概念理解的关键问题，即如何体会图形的周长就是图形一周边线的长度。有了关键问题，就有了引导学生认识周长的关键活动——你能把下面图形一周边线的长度用一条线段表示出来吗？

2.用整体视角构建周长的长度标识

通过整体解读，我们把握了新课标中关于“线的认识”和“周长的认识”之间的内在联系，从而构建了以边线为关键的学习活动。那么图形的边线有什么特点呢？可以发现边线的数量不一样、长短不一样：有些图形的边线是由三条线段连起来的，有些是由四条线段连起来的，有些是由一条线段包围起来的；边线有的长，有的短。从边线到边线的长度，边线就具有了长度的标识。

“认识周长”的关键问题就是如何引导学生构建周长的概念，因此，我们可以设计如下的学习活动，让学生用一条线段把下面图形的周长表示出来，进一步理解概念，感悟算法。

这条线段的长就是这些图形的周长，作图的过程就是构建算法的过程。明白了算理，算法自然而然就会出现。

3.用整体视角构建周长与面积的内在联系

周长是封闭图形一周边线的长度，面积就是封闭图形一周边线里面部分的大小，两者都与边线有关。通过边线，我们可以把周长和面积联系在一起，引导学生基于边线从整体视角上构建周长和面积的知识结构。

认识面积首先要理解什么是面积，就要思考什么是面？面在哪里？我们可以发现对于边线的理解是构建面积概念的一把钥匙。“面”的造字本义是：在“目”的外围加一个框，表明那个范围内是人的面部（如下图）。从面的含义引申到物体的表面，我们就能清楚地描述什么是“面”，如在黑板的外面加个框，这个框里面的范围就是黑板的面；三角形三条边里面的范围就是三角形的面；圆的曲边里面的范围就是圆的面；平面图形边里面的范围就是这个平面图形的面。周长和面积基于边而得到了很好的区分。

整体视角下的课标研读能有效提升教师的整体意识，有助于教师从大单元的角度研读新课标，把握教学内容，实施基于课标系统性理解的教学实践。

（二）要以切磋琢磨催发课标的有效落地

我们要仔细琢磨新课标的要求，深入理解新课标要求的具体含义。明白了做什么，才能设计怎么做的程序和方式。例如研读“用数对确定位置”的课标内容，我们应从新课标的描述中寻找关键词，进行细节研磨，在细节解读中寻找行动的方向和实践的力量。

1.课标研读要强化关键词的含义理解

新课标中有这样几个关键词：数对、有序数对、点、对应。我们要深入研读这几个关键词的含义，琢磨什么是数对？如何引导学生体会和构建有序数对？如何凸显点？如何理解数对与点的对应？如何在图形运动的过程中体会点的位置变化？

数对是一个表示位置的概念，是一种由两个数组成的描述物体位置的数学语言，这两个数是有序标记的，只有有序标记的数对才能很容易地判断出某一处的位置。数对可以确定学生在教室的位置，可以确定建筑物在城市的位置，可以确定一个城市在地球上的位置，可以确定一个点在平面上的位置。一个点对应一个数对，一个数对对应一个点。

对于这些关键词的思考和琢磨，有助于我们更好地理解和研究数对的教学。

2.课标研读要琢磨数学语言的形成过程

我们应注意研读课标所要求的“能在方格纸上用有序数对（限于自然数）确定点的位置，理解有序数对与对应点的关系，形成空间观念”。学生利用数对确定位置的过程就是在经历和发现“数对”作为一种数学语言形成的过程。

教材出现的素材是张亮同学有问题要咨询老师，他的灯亮了，老师马上能知道他的位置在哪里。那么老师是如何确定位置呢？她是用什么方法来描述位置的？可以发现，老师是用了下面的数学模型来确定“我”的位置的。

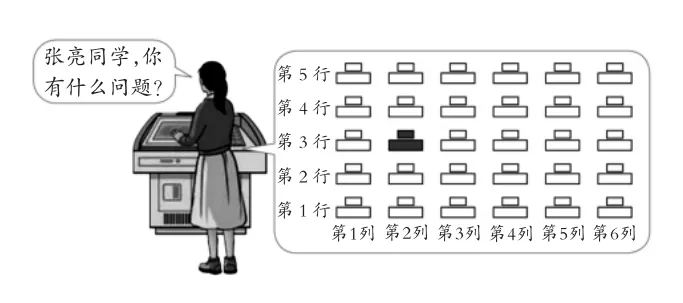
在数学活动中，学生尝试用自己的方法去描述老师是如何确定“我”的位置的，体会数对表示和确定位置的作用，感受有序数对的标记过程，体会有序数对和方格纸上的点的对应关系。在此基础上，如果把教室里的每位同学看成一个点，那怎么标记老师的位置？用什么数对描述老师的位置？

通过细节研磨，我们就可以细化课标要求，明确数学语言的形成过程，引导学生通过学习活动体会用数对确定位置和有序标记的特点，感受数对在数学发展史上的价值和意义。

3.课标研读要细化数学活动的设计指导

新课标的教学提示“引导学生通过图形位置的表达，理解坐标的意义；通过图形运动的观察和表达，体会坐标表达的重要性”。这实际上就是对课堂数学活动的具体指导——要表达图形的位置，要观察图形的运动，要表达图形的运动。

在引导学生构建了用“有序数对”的数学语言来确定教室中同学的位置、老师的位置后，应让学生思考：看到A（2，2）、B（5，1）、C（5，5）、D（5，7）、E（6，6）这5 个点，你能知道什么？可以知道B、C、D 在同一列，在同一条直线上。通过进一步思考或者画点，学生会发现A、C、E 也在同一条直线上。像这样和它们在同一条直线上的点还有哪些？你能写出多少个？你能用一个数对把所有的点都表示出来吗？

正如新课标中所说的“通过图形位置的表达，理解坐标的意义”，坐标不但可以表示出点和图形的位置，还可以把图形的相关信息用数去描述，用数的形式去描述图形的“象”。不同数对反映出来的不止是点的变化，更能反映出变化中的不变。学习活动设计应在新课标的指导下，探索如何通过活动让学生用点的变化来描述图形的变化，体会新课标所强调的“坐标的意义”。

（三）要以结构思维凸显课标的内在一致

课标研读要有结构化思维，要思考学习内容的内在一致性。通过知识发生发展的起点和终点，认真领会和感悟课标中强调的一致性，引导学生构建具有一致性的认知结构。例如笔算乘法，如何实现从多位数乘一位数到两位数乘两位数的迁移，凸显内在结构的一致性呢？

1.乘法笔算根起于口算

新课标强调要“理解算理与算法之间的关系”，可以说口算就是整数乘法的算理，笔算就是整数乘法的算法。笔算乘法就是把口算的过程表示出来，口算是笔算乘法的根，学好口算才能进行笔算。比如在学习笔算12×3 之前，教材都会安排口算，也就是引导学生研究笔算的算理。

对于12×3，我们需要注重从运算的意义出发，数形结合，借助几何直观让学生清晰地发现12×3就是这样的3 个“1 捆”和3 个“2根”合在一起，用乘法的数学语言描述就是10×3 和2×3。这样就有了三步口算过程：10×3＝30，2×3＝6，30＋6＝36。其中，对“10×3”口算算理的理解非常重要，因为这是计数单位第一次参与运算。显然它和以前学习过的表内乘法1×3是不一样的，不能直接用口诀计算。我们需要关注的是不同的乘法算式背后的相同之处，寻找背后的本质。要理解如下问题：真的不能用口诀计算吗？怎样才能用口诀计算？能用口诀计算的关键是什么？可以发现，如果把0 藏起来，那么算式10×3 就变成了1×3，就可以利用口诀“一三得三”直接口算。能把0 藏起来吗？用什么方法把0 藏起来？就是利用计数单位，用“1 捆”的表象把0 藏起来，变成了1 捆一组，有这样的三组，“一三得三”就被凸显出来了。两者都可以用乘法口诀“一三得三”来计算，一个是（1×3）个一，一个是（1×3）个十，本质是一样的。

通过口算学习，有了基于计数单位的算理理解，就能为乘法竖式笔算的描述和表达做好铺垫。

2.乘法笔算是以竖式的形式记录口算的过程

“多位数乘一位数”恰好处于从表内乘法到乘法笔算过渡的关键节点，是引导学生以竖式算法描述乘法计算过程的重要契机，是乘法竖式的第一次亮相。如何用一个竖式把口算的过程记录下来呢？这就成了本课学生学习活动的任务。

那么如何用一个竖式把口算过程都记录下来？学生会怎么记录呢？他们创造的竖式能把口算的过程记录下来吗？在实践中，我们发现学生呈现了很多作品，凸显了自己思考和创造的过程。

学生学习活动的成果充分体现了学生自主探索用竖式的形式表达算法的过程，凸显了乘法口算和乘法笔算的内在联系，口算换了一种形式被记录下来，成为描述学生运算过程的数学语言。

3.乘法笔算要感悟从未知到已知的转化

新课标提出“感悟从未知到已知的转化”，就是强调要以结构化的思维去寻找未知和已知之间的相同结构，构建两者内在的一致性。两位数乘两位数是基于多位数乘一位数的学习经验之后，乘法竖式的再次登场。从运算的一致性上来说，两位数乘两位数的关键也应当是如何把口算的过程在竖式上表示出来。

那么两位数乘两位数该如何口算？怎么把口算的过程在竖式上表示出来呢？这是基于结构一致性的从未知向已知转化的关键节点。学生应先思考如何口算，再尝试把自己的口算过程用点子图表示出来，进而思考哪种口算过程可以在竖式上表示出来。

所以，我们应当设计如下的学习活动：

14×12 与14×2 有什么不同？它有哪些口算？它又是怎么把口算用竖式表示出来的？重点不是如何口算，重点是如何把你的口算方法在竖式上表示出来。通过学习活动，学生会发现能在竖式上表达出来的口算只有两种：14×10＋14×2 或者12×4＋12×10。

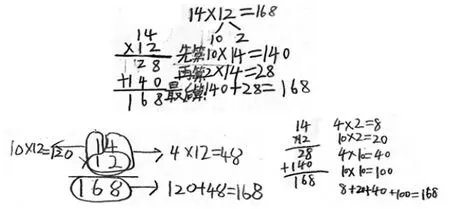
竖式笔算的过程就是把口算的过程表示出来，就是在原有竖式笔算的基础上添加了一步新的口算，而在这个口算描述的过程中，学生会发现14×2 应当作为口算过程的第一部分直接进行口算，这也是教材专门编排了类似14×2 的口算教学内容的原因所在。学生的已知是用竖式表示口算的过程，未知向已知的转化就是要思考有哪些口算，该怎样把这些口算简洁地在竖式上表示出来，这样就使得整数乘法的竖式笔算具有了内在的一致性。

总之，面对新课标研读在实践中遇见的困惑，我们应以整体视角明晰新课标的系统性，以细节研磨体会新课标的有效性，以终始梳理凸显新课标的一致性。新课标是值得一线教师反复研读的经典，需要在实践中去运用。我们要依标施教，要学会用课标，而不是纠结于新课标概念文字的意义。我们要用自己的教育人生和教育智慧与经典进行研磨，在研磨中不断解惑，不断有新的实践路径和发现。