把握概念本质 破解疑难问题——以《轴对称的再认识》一课为例

文|徐小巧

【教学内容】

人教版四年级下册第七单元。

【课前思考】

《轴对称的再认识》是在二年级初步认识轴对称图形的基础上，用“对称点到对称轴的距离”等定量刻画的方法来进一步分析图形的特点。在磨课的过程中我们发现学生有以下两处疑难和困惑点。

疑难点1：学生很难判断平行四边形是不是轴对称图形。（这节课所讨论的平行四边形指的是一般的平行四边形，不考虑特殊的平行四边形）

我们对全校8 个班级近400名学生进行了前测。从数据分析发现接近的学生认为“平行四边形是轴对称图形”，在和学生的访谈中发现学生是把平分线和对称轴混淆了，误认为平分线就是对称轴。

疑难点2：学生很难体验到轴对称也是图形的一种运动方式。

教材把“轴对称”纳入《图形的运动》这一单元，是把“轴对称”理解为图形的运动方式。在第一学段的学习中学生对轴对称图形的认识是停留在静态层面的“两边一样”，由于轴对称更多的是呈现运动后的结果，所以学生很难体验轴对称是一种图形的运动。在前测中，我们发现一个班只有3个学生认为轴对称是图形的运动，通过访谈这3 个学生的理由分别是：随便猜的；对折是运动；轴对称是图形转起来的。

怎样才能让学生真正理解轴对称概念的本质？笔者认为可以基于学生的疑难点，以“平行四边形是不是轴对称图形”这一核心问题引领学生进行深度学习，去探索和发现轴对称图形的本质特征。因此把例1 单独作为一课时来研究。

【教学过程】

一、了解起点，初步感知特征

1.数据分析，激活已有知识

师：通过前测，老师发现特殊的平行四边形同学们都能正确判断出它们是轴对称图形，而对这个普通平行四边形的判断，意见不太统一。

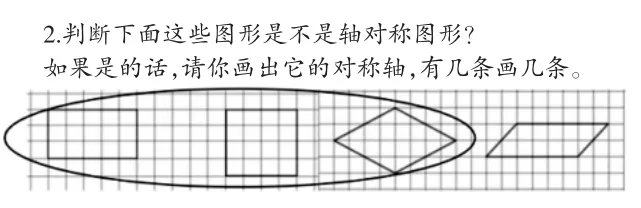
师：有16 位同学认为像这样一般的平行四边形不是轴对称图形，有32 位同学认为是轴对称图形，并画出了这样几条对称轴。那么像这样普通的平行四边形是不是轴对称图形？这几条到底是不是它的对称轴呢？你有什么办法可以来验证一下？

生：可以折一折，把平行四边形对折，看看对称轴的两边有没有完全重合。

生：可以用照镜子的方法，看看镜子中的图像和图形的另一半是否一样。

2.借助操作，初步感知特征

●活动一：验证这几条平分线是不是平行四边形的对称轴？

（1）学生活动。

（2）反馈：你选什么方法验证，验证结果是怎样的？

照一照：学生上台演示（几何画板验证）。

折一折：学生上台演示（几何画板验证）。

（3）过渡：通过对折和照镜子都可以确定这几条都不是平行四边形的对称轴，那为什么不是呢？如果是轴对称图形又要具备什么特征呢？我们选其中的3 个轴对称图形来研究一下。

二、任务驱动，探究本质特征

1.“对称点”的研究

师：在这个轴对称图形里沿对称轴对折，你能找到与A 点完全重合的点吗？

学生上来找一找，课件演示对折验证。

揭示概念：在轴对称图形中沿对称轴对折能完全重合的两个点叫对称点（板书）。

师：你能在图②③中也找一组对称点吗？（课件对折验证）

质疑：刚才第①幅图找对称点时你们是上下找的，怎么图②要左右找，图③要斜着找？

生：因为对称轴的位置变了，所以对称点的方向不一样。

小结：对称点的位置和对称轴有一定的关系，到底有怎样的关系？是不是每一组的对称点和它的对称轴都有这样的关系呢？

2.自主探究特征

●活动二：探究每一组的对称点与对称轴之间有什么关系？

师：在探究的过程中你发现了什么？

生：对称点到对称轴的距离相等。A 点到对称轴的距离是2 格，A′点到对称轴的距离也是2 格。

师：图①中有这样的关系，那其他两个图形呢？

生：B 点和B′点，C 点和C′点到对称轴的距离也是相等的。

小结：看来，对称点到对称轴的距离相等（板书）。

生：对称点连线与对称轴互相垂直。连接对称点，它们的连线和对称轴是互相垂直的。

师：刚才找对称点的时候，一会儿上下找、一会儿左右找、一会儿斜着找，原来是对称点的连线要与对称轴互相垂直（板书）。

小结：一组对称点不仅点到对称轴的距离相等，而且对称点的连线和对称轴是互相垂直的。

3.根据特征找对称点

师：这个轴对称图形上还有其他的对称点吗？请你找一找。

反馈：学生指出网格交叉位置上的对称点。

师：你是怎么找的？

生：在左边找一点，数一数到对称轴是几格，再往右边数几格。

生：还要看这两个点的连线有没有和对称轴互相垂直。

生：还有在图形的边上但不是网格交叉位置的对称点。

生：对称轴上的对称点。

师：对称轴上为什么只看到一个点？

生：因为现在这两个点重合了。

师：像这样特殊的对称点还有吗？在哪里？

生：还有很多，在对称轴上。

生：图形里面的对称点。

师：刚才在找对称点的过程中，有没有什么发现？

生：一个轴对称图形中有无数组对称点。

生：轴对称图形中的每个点都能在对称轴的另一边找到它的对称点。

小结：轴对称其实是一种图形的运动，对称轴就像是一面镜子，图形左边的点照到到镜子里，镜子就会反射出它的对称点。不管这个点在线上、对称轴上还是面上，只要是轴对称图形，图中所有的点都能在对称轴的另一边找到它的对称点。

三、对比辨析，深刻理解本质

过渡：现在我们回过头来看刚才这道题，你能用今天所学的知识来解释和说明这些线为什么不是平行四边形的对称轴吗？

1.利用特征，辨析难点

●活动三：选一幅图说说这条线为什么不是它的对称轴？

生：我选的是②号，如果这条是它的对称轴，那么左右两个点到对称轴的距离要相等，现在一个是2 格，一个是4 格，距离不相等，所以不是。

生：我选的是①号，如果这条是它的对称轴，那么上下两个点的连线要和对称轴互相垂直，现在没有互相垂直，所以不是。

小结：可以根据刚才发现的特征来判断。要么两个点到对称轴的距离不相等，要么两个点的连线没有和对称轴互相垂直，所以这几条都不是对称轴。

2.借助直观，突破难点

师：那为什么会有那么多的同学会认为是对称轴呢？

生：因为这些线把平行四边形分成两个完全一样的图形。

师：原来这些线把平行四边形平分成两个完全一样的图形，所以很容易和对称轴混淆。看来，平分线并不一定是对称轴。

师：像这样的平分线在平行四边形中还有很多很多，那会不会有一条正好是它的对称轴呢？

师：如果以这条线为对称轴，能想象形成的轴对称图形吗？那形成的这个图形会不会和平行四边形重合？（课件演示转动一圈）

小结：以平行四边形中所有的平分线为对称轴形成的轴对称图形都没有和平行四边形重合，所以像这样的平行四边形不是轴对称图形。

四、动态想象，深化概念本质

师：刚刚我们研究的对称轴都在图形的里面，如果把对称轴移到平行四边形的外面，假设对称轴是一面镜子，能想象形成的轴对称图形吗？（课件演示）这时它还具备轴对称图形的两个特征吗？

想象：如果改变一个点的位置，那它的对称点怎么变呢？

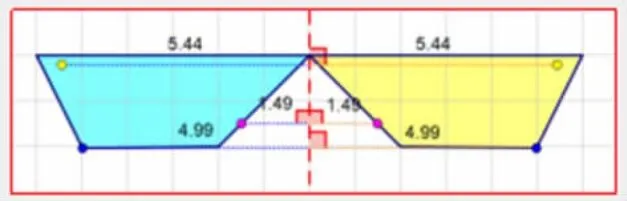
师：如果左边的点向上移3格，右边的对称点怎么变？

生：右边的对称点也向上移3格。

师：如果左边的点向下移3格呢？

生：右边的对称点也跟着向下移3 格。

师：向右移3 格呢？

生：向右移3 格。

生：不对不对，往左移3 格。

师：静静思考一下，说说理由。

生：左边的对称点往右移3格，它离对称轴的距离靠近了3格。如果对称点到对称轴的距离相等，那么右边的点也要靠近3格，所以应该是往左边移3 格。

师：这跟生活中的哪个现象很相似？

生：很像照镜子，我们走近一点，镜子里的像也会近一点。

师：那向左移3 格呢？

生：右边的对称点往右移3 格。

师：现在你有什么想说的？

生：点的位置变了，对称点的位置要跟着变。

生：对称点位置变化的过程中轴对称图形的两个特征始终没变。

继续想象：如果改变对称轴的位置，这两个特征还会不变吗？

生：不管对称轴的位置怎么变，只要是轴对称图形这两个特征始终不变。

小结：不管点怎么变，对称轴的位置怎么变，对称点到对称轴的距离始终保持相等，对称点连线与对称轴始终保持互相垂直。只有符合这样的两个特征才是轴对称图形。