图解数学 让思维动态化——以“烙饼问题”教学为例

文|梅茜茜

“图解数学”指的是运用图形、表格、公式等可视的方式把学生本来不可视的思维（思考方法和思考路径）呈现出来，使其清晰可见。小学数学随着年级上升，数学问题逐渐变得既抽象又复杂，图解数学一方面可以让学生更好理解数学，另一方面可以让学生的思维可视化、动态化。

一、基于图解数学的教学思考

“烙饼问题”属于数学广角的教学内容，通过生活中常见的烙饼事例，让学生从数学角度出发，经历从多种解决方案中寻找最优方案的过程。很多教师在上这一内容时，很容易把握错方向，将其上成找规律、找公式的课，忽略学生的思维培养，导致课堂上总是成绩好的学生在唱独角戏，而更多学生往往只会套用公式，题型稍一变化就完全一头雾水。所以，从培养学生思维的长远目标来看，本节课的主要目标应是归纳和演绎经验的积累，而“优化”则是学生思维活动中所感悟的数学思想。

教师真正要关注的是学生在烙饼问题中的思维变化过程，尤其是学生在面对3 张饼的最优烙法时，源于日常生活经验，大部分学生第一反应是常规烙法——先烙两张饼，再烙一张饼。学生一开始很难想到3 张饼最省时的烙法是交替烙。图解数学这一方式就可以很好地解决这一难点。让学生通过摆实物图的方法，直观呈现3 张饼交替烙的思维过程，通过对比发现烙饼省时的关键在于让锅没有空余。但这时，学生的思维是片段式的，他们掌握了同时烙和交替烙这两种方法，但是对于更多的饼数，有一定的思考难度。接着，让学生脱离实物，利用动手画图来寻找4 张、5 张饼的最优烙饼方案。这些小数据的探究经验，再结合有序地观察烙饼记录表，学生会发现原来所有饼数的优化烙法都可以利用同时烙和交替烙来解决，进而找出饼数与烙饼时间的关系。学生在一次次的观察中发现、一次次的探究归纳中积累经验，通过图解过程，让思维动态化，帮助学生建立连贯完整的思维过程。

二、教学实践探索

（一）实物模拟——呈现思维的动态化

出示情境图：小红妈妈烙饼，一个锅每次最多烙两张饼，两面都要烙，每次3 分钟。

师：小红妈妈早上为小红和爸爸各准备一张饼。猜一猜，时间是多少？

生：需要6 分钟。

师：你能上来边演示边讲述烙饼过程吗？

生：第一次烙两张饼的正面，第二次烙两张饼的反面，两次一共6 分钟。

?

师：为什么不一张一张的烙？

生：这个锅最多可以放两张饼，一张一张的烙也可以，只是浪费了空间。

师：所以，想要烙饼时间最少，就要完全利用锅的最大空间，实现效率最大化，从而达到“尽快”的目的。两张饼同时烙，一共烙了两次，时间是2×3＝6（分钟）。

师：如果妈妈自己也需要一张饼，烙3 张饼，最少需要几分钟？同学们先静静地独立思考，然后小组同学一起借助圆饼模型摆一摆。

师：哪个小组愿意和大家分享一下你们的方法？

生1：（一人负责演示，一人负责讲解）我们小组烙了4 次，12 分钟。第一次烙正1 和正2，第二次烙反1 和反2，第三次烙正3，第4次烙反3。

生2：我们小组只需要3 次，9分钟。第一次烙正1 和正2，第二次烙反1 和正3，第三次烙反2 和反3。

第一组第二组第1 次正1正2正1正2第2 次第1 次第2 次反1反2正3反1正3反2反3反3

师：他们两组有什么不同之处？

生：第一组烙了4 次，前两次同时烙2 张饼，导致第三次和第四次锅里有空余位置。第二组利用了锅的最大空间，让每次都有2张饼烙。

师：有什么共同特点吗？

生：3 张饼都需要烙6 个面。

师：3 张饼6 个面，每次最多能烙2 个面，按计算只需要烙3次，为什么第一组需要4 次？

生：他们组第3 张饼不能同时烙正面和反面。

师：如果不想让锅有浪费，3张饼最关键是第几次的烙法？

生：第2 次。

师：是的。把3 张饼6 个面看成一个整体，第2 次烙第3 张饼的正面和第1 张饼的反面，这样一交替，能使第3 次也有2 张饼可以同时烙。这就是交替烙。

从2 张和3 张这样的小数据出发思考，再到接下来的大数据探究，符合该阶段学生从特殊到一般的认知规律。通过实物图解2张饼和3 张饼，既使抽象的烙饼问题具体化，也激发了学生的探究兴趣。

在教学3 张饼时，呈现两组同学的不同图解过程，相当于直观呈现了以这两组为代表的两种思考过程。教师通过层层递进的问题，让学生不断对问题进行思考，真正理解何为交替烙。每一次的探究都是一次宝贵的经验，为下一步的探究做铺垫，让学生的思维找到支撑点，达到层层递进思考的目的，培养其逻辑思维能力。

（二）画出过程——凸显思维的运动化

师：有了之前的经验，对于更多的饼数，你敢挑战吗？请思考4张、5 张饼如何烙？

发现学生呈现两种图解，一种是2+2 同时烙，另一种如下图所示，学生刚学完交替烙，自然而然就有部分学生用这种方法。烙4 张饼

第1 次正1正2

第2 次正3反1

第3 次正4反2

第4 次反3反4

烙（4）次，所需最少时间：4×3=12（分钟）

师：4 张饼的两种烙法你们觉得哪种更方便？

生：两张两张同时烙更方便。

通过两种图解的对比，让学生理解“优化”的真正内涵。有了这样的体验，学生在思考5 张饼的时候，会更多地思考如何在操作上更优化。

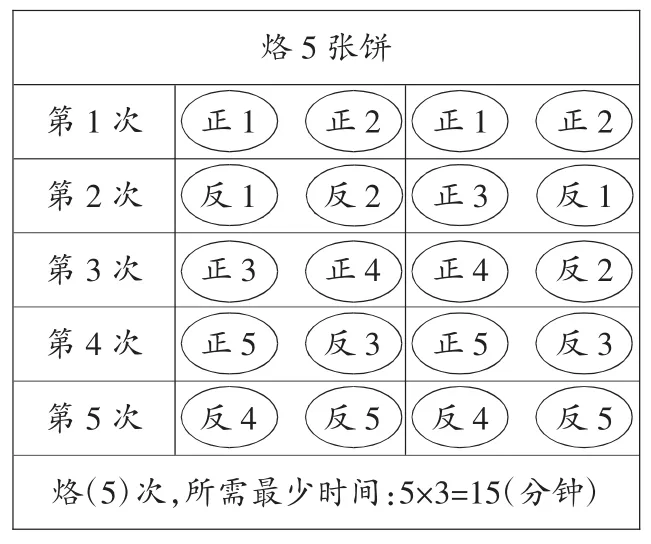
烙5 张饼第1 次第2 次第3 次第4 次第5 次正1正2正1正2反1反2正3反1正3正4正4反2正5反3正5反3反4反5反4反5烙（5）次，所需最少时间：5×3=15（分钟）

师：两种方法，你们觉得哪种更能看懂？

生：第1 种方法，将5 拆成了2 和3，先同时烙再交替烙，这样更方便。

在比较的过程中，让学生的思维产生碰撞，当问到6 张饼时，学生自然而然会想到既可以2+2+2，也可以3+3。从常规烙法到最优烙法，学生的思维跨度很大，他们的思维不再只停留在低阶思维，真正理解了“优化”的数学思想。

（三）发现模型——感悟思维的运动价值

出示表格，利用之前所得到的图解经验思考更多饼数的烙饼方法。

师：观察这张表格，思考7张、8 张、9 张、10 张甚至更多饼数时，怎么烙？

饼数（张） 最省时的烙饼方法 烙饼所需最少时间（分）2 （2）同时22×3＝6 3交替33×3＝9 4 （2+2）同时44×3＝12 5 （2+3）同时+交替 55×3＝15 6 （2+2+2）（3+3）同时/交替 66×3＝18次数

生1：7 张饼可以拆成2+2+3来烙。

生2：8 张饼可以2 张2 张的烙。

生3：9 张饼可以拆成2+2+2+3，也可以3+3+3。

师：那100 张饼呢？

生：可以2 张2 张的烙。

师：101 张饼呢？

生：前面都2 张2 张的烙，最后3 张交替烙。

师：能总结一下烙饼的方法吗？

生：当饼数是双数时，都可以2 张2 张的烙。

生：当饼数是单数时，可以先2 张2 张的烙，最后3 张交替烙。

学生在探究2 张到6 张饼的烙法之后，对于更多的饼数不需要再进行实物操作或画示意图，学生发现只需要把饼数拆成若干个2 或者若干个2 和一个3。前期图解“烙饼问题”，让抽象问题具体化。现在借助表格，由具体化进阶到抽象思考。在思维方式转化中，学生的思维得到进一步有效的激活。

（四）反思规律——提升思维的活跃深度

师：同学们，请看我们经历的这些烙饼经验，你能找到烙饼最少时间的规律吗？

生1：最少时间＝烙一面饼的时间×烙饼次数。

生2：这里烙饼的次数就等于饼的张数，所以，最少时间＝烙一面的时间×饼数。

师：为什么饼数会等于烙饼次数？

生：因为我们要利用锅的最大空间，一个锅可以烙2 张饼，烙饼次数＝饼数×每个饼要烙两面÷一个锅最多放2 张＝饼数。

师：对于这个规律有什么要补充吗？适合所有的饼数吗？

生1：不适合一张饼，因为一张饼，每次只能烙一面，要烙2次，不是1 次。

生2：不适合，这个规律算出来是3 分钟，1 张饼正反都要烙要6 分钟。

师：这个规律适合一个锅每次烙2 面，而且饼数至少是2 张。

通过质疑引导学生发现饼数和烙饼次数之间的必然联系以及这个规律的局限性，让学生的思维严谨性进一步得到提升。

（五）变化情境——拓展思维的训练广度

师：假如现在一个锅每次最多能烙3 张饼，两面都要烙，每面3 分钟，烙4 张饼最少时间是多少？怎么烙？

生：我是用画图的方法，最少时间是9 分钟。

师：图解不失为一种好方法。如果是123 张饼呢？怎么烙最省时？最少时间是多少？

生：锅最多放3 张饼，可以每次都3 张3 张的烙，这样123 张饼可以拆成41 个3，3 张饼需要6分钟，所以最少时间是41×6＝246（分钟）。

在前面的学习中，学生已经知道烙饼问题的本质就是空间最大化利用。在这些经验的铺垫下，即使变换情境，他们也可以用归纳转化的方法得出结论。这个环节的设计让学生的思维从一个一般规律到另一个一般规律，从而拓展思维的训练广度，提升学生的思维水平。

三、实践反思

在“烙饼问题”的教学实践过程中，充分体现了图解数学的优越性。图解的方式能把学生的思维直观地呈现出来，让教师清楚地了解学生的思维状态。同时，学生在图解的过程中，本身就是对题目进行抽丝剥茧式的直观呈现，能使学生打开思路，从而让学生充满探究动力，让一堂课更加生动别致。

图解数学，让学生的思维真正做到动态化、运动化。从“烙饼问题”这节课中我们也看到学生的思维是一个动态发展的过程，通过一系列的观察、操作、归纳、总结、转化，让学生的思维得以提升，促进学生思维发展。