基于预学的单元整体性教学——以『多边形面积』单元教学为例

文|卢成水

学生的学习是一个认知建构的过程，单元是教材的最小整体。小学数学学习如何体现学生的学习特点,如何体现单元知识的整体性呢？下面以“多边形面积”这一单元教学设计与实施为例加以阐述。

一、系统思考，整体把握教材内容

单元整体教学，教师要有系统的思想观念，着眼知识体系，整体把握教材内容。纵向梳理知识线，横向吃透知识本质，是整体把握教材内容的两大策略。

1.前延后伸，纵向了解知识主线

图形的认识和测量，贯穿于整个小学阶段。在第一学段、第二学段分布的时间轴如下：

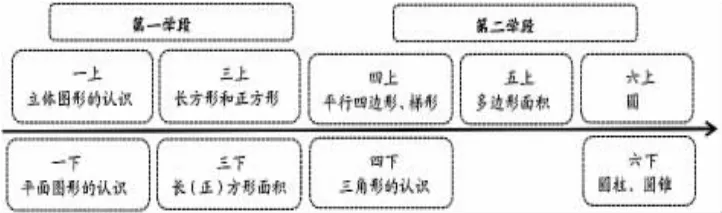
通过纵向梳理可知，小学阶段平面图形面积的学习，是循序渐进、螺旋上升的，也是后续学习立体图形表面积、体积的基础。

2.归一类化，横向吃透知识本质

在小学图形面积的编排中，以长方形的面积作为基础，以图形转化推导平行四边形、三角形、梯形、圆的面积计算方法，体现出“归一类化”的思想方法。知识背后的思想方法，是需要让学生着重理解和领悟的。

小学阶段还有许多知识是相似的。如长度、角度、面积、体积的测量和质量、时间、人民币等知识，实质都是单位的累加，只是单位、进率不同。吃透知识的本质，是为了教学中更好地把握教学的重点。比如，从整体教学的角度，让学生学会整体迁移，举一反三，从学一例到会一类。

二、搜集证据，切实把握学生学习起点

把握学生的学习起点，找准教学的切入点，解决学生需要解决的真问题，让学习真发生。我们用预学和前置性作业的形式来了解学生的学习起点。

1.基于学情基础，设计单元预学前置作业

（1）布置前置性长作业。

以上预学与前置性长作业，学生在较长时间内完成。学生完成作业生成的想法，为课堂教学提供了丰富的学习材料，为学生展开比较、辨析、对话等提供了范例，为教师教学推进提供了素材。

（2）梳理问题。

“多边形面积”学生提出的主要问题见下图。我们将问题分两类：①至④是基础类，⑤至⑧是延伸拓展类。预学中学生发现并提出自己心中的真问题，在重点课例中和伙伴们一起探究并解决，这才是真正有效的课堂教学。

（3）分析作业。

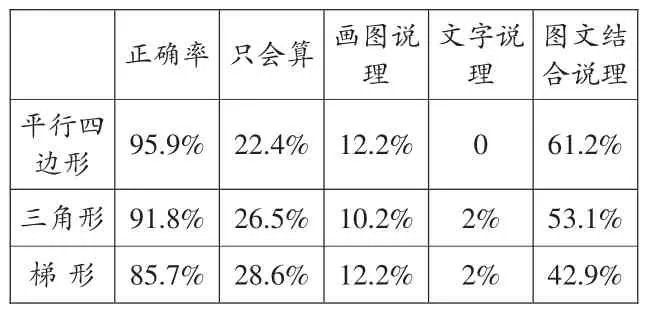
“多边形的面积”预学情况统计表

从上述统计表可看出，大部分学生能量出需要的数据，算出图形的面积。错误主要有：平行四边形的面积用两条邻边相乘，三角形和梯形的面积没有除以2，梯形的面积个别没有乘高或加上底。正确的学生大部分能用不同的方式说清楚道理，图文结合说道理的学生对图形间的关系已经很清晰了。只会算的学生，有的是套公式不懂道理，有的口头会说，但不会用图或文字表达。

全面分析前置性作业情况，才能精准把握难点，明确后续教学的方向和目标。

2.结合作业情况，整体设计单元教学结构

基于单元预学，这一单元的课堂教学，我们确定了两大重点：一是帮助不会的、只会算的学生理解公式背后的道理；二是对单元核心问题的再突破，即培养学生的空间观念。

基于此，对教材原来的编排顺序、教材内容适度调整，重构单元框架、课时目标见下表1：

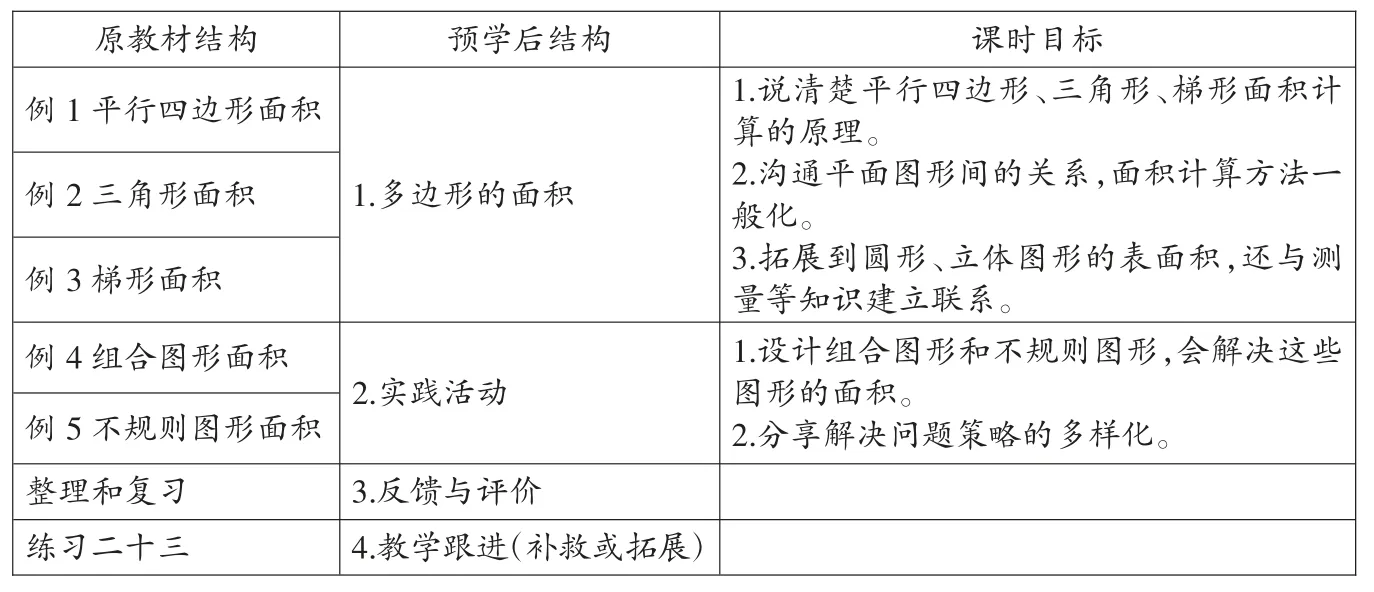
表1

经过调整，教材中的例1 到例3，整合为一课时，解决单元核心问题，以及学生提出的8 个问题。例4、例5 整合为一节实践活动课，课前长作业与课内集体反馈交流相结合。反馈与评价主要检测对单元基础知识的达成情况，如果问题大就补救跟进，反之就拓展。需要特别注意的是，单元整体教学绝不是为了节约课时，而是在更精准把握学生学习起点基础上，让学生学得更充分、更扎实、更有价值。

三、整体设计，打破课时教学思维

充分利用预学材料，引发有价值的教学互动，让学生经历更充分的知识建构过程。

1.“多边形的面积”一课

环节一：说道理

（1）整体呈现。

呈现预学材料中大家的想法。问：在研究平行四边形、三角形、梯形的面积时有什么相同和不同的地方？突出都是把新问题转化成已经会解决的问题，但转化时用的方法不同，如平行四边形采用割补法等积变形，三角形、梯形还可采用拼的方法。

（2）学具操作。

首先要帮助学习有困难的学生，借助动态演示理解面积计算的原理。其次要解决小核心问题，如为什么沿着平行四边形的高分？只能沿着这条高分吗？为什么拼上同样大小的三角形或梯形？只有在这样的前提下，上述的想法才是成立的。数学要具有科学性。

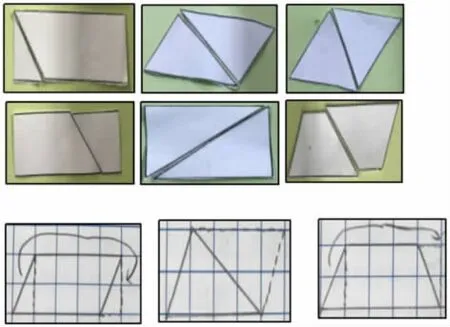
（3）补充想法。

由于是学生预学后测试的，所以想法比较集中。此环节要补充想法，感受转化方法多样化。如三角形也可以割补成长方形或平行四边形，梯形也可以分割成两个三角形或一个平行四边形和一个三角形等，防止学生思维定势。

环节二：找联系

此环节，一是要与学习长方形面积的方法建立联系，二是将这四个图形面积计算方法类化。分两个层次：

第一层次：（1）回忆：长方形面积用长乘宽，是怎么研究的？（2）在研究平行四边形、三角形、梯形面积时，用数面积单位的方法了吗？

第二层次：这四个平面图形的面积计算方法，能不能只记一个，记哪个更合适？长方形、平行四边形可以看成上底、下底一样长的梯形，三角形可以看成上底是0 的梯形，这四个平面图形都可以看成梯形。

环节三：会拓展

此环节中继续转化和迁移，解决圆形的面积如何研究。另外，还可以与测量等知识建立联系。

问题一：圆形的面积，你能想办法知道吗？立体图形的面积呢？下左图，用外切、内接正方形的方法，用估算；下右图，用分割，转化成近似的长方形或平行四边形。立体图形的面积就是几个面的和，也就是表面积。

问题二：测量平面图形的面积用面积单位累加，小学阶段哪些知识也是这样的呢？面积、长度、角度的测量，以及后续要学的体积、容积等知识，也都是单位的累加。

2.“实践活动”一课

（1）布置前置性长作业。

内容：设计组合图形和不规则图形，计算出面积，说明这样算的理由。

要求：回家作业，独立完成。

（2）课内反馈。

集体展示，分规则图形和不规则图形两个环节，主要反馈想法的合理性，重点是不规则图形的反馈。

①猜猜：这两幅作品是怎么解决的？

左图采用分，用三角形的面积+长方形的面积=组合图形的面积；右图，有两种方法，方法一是左边长方形+右边两个小三角形的面积=组合图形的面积，方法二把这个组合图形补成长方形，用大长方形的面积—补的小三角形的面积=组合图形的面积。

②下面这些不规则图形的计算方法，你同意吗？为什么？

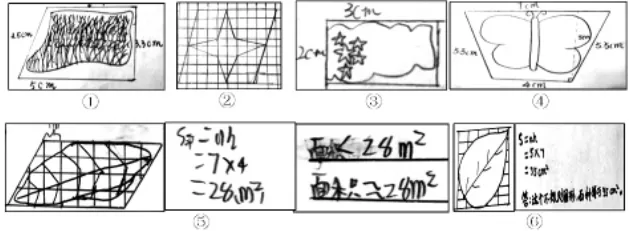
引导学生先“阅读”别人的想法，教师再反馈。其中，图④⑤的想法正确；图③国旗是规则的长方形，不能随意改动；图②看成平行四边形，面积相差大不合理，可以分成四个小三角形加一个小正方形；图①看成平行四边形更合理；图⑥树叶的面积小于35 平方厘米。在反馈中，体验合理与不合理，感悟数学的科学性，生活的真实性。

四、基于系统思维的单元整体教学实践感悟

单元预学后的整体教学，教与学的行为都发生了明显的变化。教师不得不整体性地思考不同课时在单元中的价值，不得不思考每一课之间的联系，不得不更关注学生的起点、经验和问题，不得不考虑单元核心概念的渗透和突破。这些转变，都要求教师不断提高自己的专业性。

学生不得不用足够多的时间静下心来自主学习，不得不用自己的方式来提取信息、提出问题、梳理知识结构等———这些都异于他们已经习惯了的学习方式，对他们而言也是挑战。实践证明，这样教学学生的阅读力、专注力、学习力、合作力、表达力、概括力、思维力等“学习力”得到了更多的锻炼。