立足教学评一致性 培养数据分析能力———《折线统计图》教学思考与实践（二）

文|董景勋

【教学内容】

人教版五年级下册第104、105 页。

【教前思考】

“双减”背景下，课堂如何提质增效？笔者以“折线统计图”为例，从“教学设计”到“课堂实践”。围绕“学生要学会什么？（学习目标）”“何以知道学会？（评估证据）”“怎样让学生学会（学习活动）”三个核心问题，立足教学评一致性，尽力提升学生的数据分析能力。

一、精准定位，立足学教方向

1.依托教材体系，把握逻辑起点

折线统计图安排于第三学段。折线统计图有利于直观了解变化的情况，预测未来的趋势。相比条形统计图，表面是从“数量多少”到“数量变化趋势”，学会数据进行分析、预测和推断。实质是需要一个新的思考方式：从“确定”到“不确定”解决问题。教材在这种思维教学方式中出现了断层，教学中要让“折线”走慢一点，解决问题思维方式转变体验走深一点，创造更多的体验和空间。

2.立足学情视角，了解现实起点

课前做了调查，结果如表1。调查发现，绝大部分学生通过各种渠道对折线统计图的概念和特点有一定了解，但是数据背景意义和数据变异感悟比较弱。特别是没有习惯依据数据进行决策，且没有意识需要更多的数据才能进行合理预测推断。

表1

二、逆向设计，落实评价任务

以“折线统计图”学习目标为起点与核心，先确定评价标准和评价任务，再安排学习，让学生始终有清晰的目标和方向。

1.对应学习目标

设计和学习目标评价，细化和厘清每个环节的目标。在销售情况、动物园客流量、身高变化中设计问题链，每个问题相互关联，富有层次。同时把三个情境浓缩成用数据进行决策、解决问题的任务群。

2.融入教学全程

课前评价了解学情，课中随时进行评价，引导学生在解决任务过程中利用打星进行反思和学习。每个活动评价任务巧妙穿插，融入全程。

【教学过程】

师：（出示表2）结合自主评价记录表，你还想知道折线统计图的哪些知识？

表2

生：折线统计图和条形统计图有什么不一样？

生：折线统计图有什么用？

师：心中有目标，学得更清楚。这节课，一起来学习这些问题。

一、自主探究，理解折线统计图的意义

课件出示三个问题情境。

●活动一：整理数据，唤醒用数据变化的角度观察

（出示表3。小组交流，教师巡视指导，交流反馈）

表3

反馈交流一：如果你是销售主管，接下来会怎么进货？说明理由。

生1：我会选择B 品牌家电，因为比A 品牌家电销售得多。

生2：我不同意，我觉得只看总数不一定准确，应该结合1～4月的销售情况来分析。

师：你的意思是要出现更多的数据，依据数据的变化趋势进行决策。（课件出示）

师：以前，总数是判断的依据，现在我们可以根据销售数量变化趋势作出决策，这是解决问题的新角度。

反馈交流二：杭州动物园游客变化情况怎么样呢？

生：游客1月最少，3月最多。

生：游客从1月到3月慢慢变多，到3月流量最多，4月和5月又开始下降。

师：你数的感觉很到位。数量慢慢上升，然后又下降。

反馈交流三：当她15 岁时，身高大约多少厘米呢？

生1：8 岁到10 岁长了10 厘米，10 岁到12 岁长了24 厘米，照这个趋势到14 岁要长30 多厘米，估计她到15 岁要到2 米了。

生2：8 岁到10 岁长了10 厘米，10 岁到12 岁长了24 厘米，12岁到14 岁又会回到长10 厘米，估计她到15 岁快到180 厘米。

生3：到12 岁就不怎么长了，估计她到15 岁差不多170 厘米。

师：预测要根据数据才能有理有据。有时候为了更合理地预测，需要收集更多的数据。

●活动二：表达数据，应用数据变化的思维解决问题

（出示表4。学生尝试画图，教师巡视指导，收集杭州动物园游客变化情况典型作品）

表4

表5

1.作品1

师：你是如何画出这些数据的？

生：我先把这些数据找到对应的点，写上数据，再连成线。

师：他表达得很完整。简单讲：选点-写数-连线。

2.作品2：不规范

师：你们需要提醒他什么吗？

生：忘了写上数据。

3.引导学生解读分析

（1）读图，解读看得见的点

师：仔细观察这些“点”，它们表示的是什么？

生：数量的多少。

（2）读图，解读看得见的线段

师：折线统计图中，每一个点都表示数量的多少。点与点之间的连线表示什么呢？

生：我觉得是游客流量的变化。

生：我觉得可以看出游客变多还是变少。

师：仔细观察线，经历几次游客的变化？

生：总共经历了四次变化。

师：先观察，游客每一次变化的数量一样吗？

生：不一样，第一次上升一点，第二次上升最多，第三次和第四次回落。

师：数据并没有告诉你数量上升还是下降，你们是怎么判断的？

生：我是看线段的长短。

生：线段角度越陡，变化越大；线段角度越平，变化越小。

小结：单独的数据看不出销售的变化，但是把它连成线就能明白数据之间的联系，就知道了旅游人数的变化情况。这也是解决问题的新角度：通过观察一连串的数据，找到事情发展的趋势。

（3）读图，解读看不见的线段

师：是什么原因让杭州动物园游客有这样的变化情况？

生：受新冠疫情的影响。

师：为了吸引更多人去参观动物园，你会想什么办法？

生：优惠政策、提高宣传度。

师：接下来旅游人数会怎么样？

小结：折线统计图能帮助我们科学分析事物、作出决策并指导生活。

●活动三：对比分析，问题解决从精确方式到变化趋势方式转变

1.对比分析统计图

师：对比条形统计图和折线统计图，独立完成填空并说清是从哪一幅图中找到的。

生：1月是5.8 万人，4月是8.5 万人，从条形统计图和折线统计图中都能找到。

师：怎么找到的？

生：条形统计图用直条表示数量，折线统计图用线点表示数量。

生：2月到3月旅游人数上升最快，从折线统计图中看到的。

生：也可以通过条形统计图看到：9-6.3=2.7（万人）。

师：这两种方法不一样吗？

生：折线统计图比较直观，变化趋势很明显，通过线的长短就知道了，而条形统计图需要算出每个月相差多少。

小结：旅游人数上升得快与慢，第一种方法可以算出每个月相差的数量；第二种用线段的长短，变化趋势直观判断。这是两种不同方法的解决策略。

生：2月中旬旅游人数约7.2万人。我从折线统计图中看到的。

师：7.2 万人是准确的数吗？

生：我觉得不是一个准确的数，每天旅游人数是不确定的。

生：我觉得也不是，是根据折线统计图的趋势大致判断出的。

师：那你是怎么找到的呢？

生：根据2月和3月两点之间，找到相应大概的数据。

师：没有一个确定的数，但是可以根据线段趋势判断大概的位置。从确定数判断到线段趋势去判断，是解决问题的新角度。

2.作出决策，感知解决问题的新角度

师：（出示图1）如果你是销售主管，接下来会怎么进货？观察A与B 品牌折线统计图，又有什么新想法？

图1

生1：我原来选的B，因为它总数卖得多，但是我现在选择A。因为通过观察折线统计图，A 数量一直在上升，而B 一直在下降。

生2：我选择A，A 是越来越多，B 是越来越少。

师：两位同学不约而同都依据什么作出判断？

生：都是销售的变化情况。

师：我们原来是根据总数作出判断，也可以根据平均数作出判断。今天我们掌握了一种解决问题的新角度，是什么？

生：根据数量的增减变化作出决策和判断。

二、合作交流，深度理解折线统计图的预测功能

●活动四：分析数据，应用数据变化的视角思考

出示小婷从出生到12 岁的身高数据，如图2，基于这个数据，预测她15 岁的身高，给出了不同答案：2 米、180 厘米、170 厘米。“实际上，她今年已经15 岁了，她的身高是168 厘米”，并得到图3。

图2

图3

问题一：预测一下小婷18 岁时的身高。

生：12～15 岁增长幅度不大，所以15～18 岁增长也幅度不大。

师：（出示其他女生身高图）实际情况是这样吗？

生1：虽然她们的身高具体数值不同，但15～18 岁变化趋势却比较一致，增长的幅度都不大，由此可以预测小婷到18 岁很可能只比15 岁时增长2 厘米左右，即她18 岁的身高在170 厘米左右。

生2：只有三个女生的数据是否太少了，不说明一般情况，还可以收集更多的数据。

（出示女生平均身高统计图）

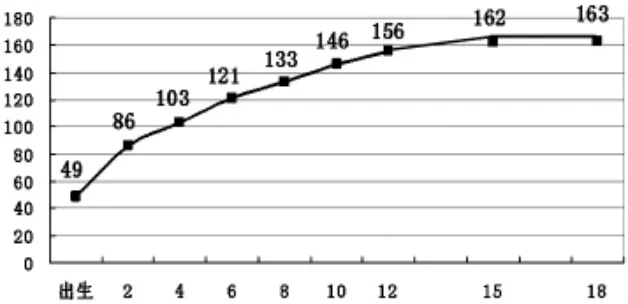
师：用更多数据可以帮助我们合理预测。

问题二：哪一幅可能是女生0～24 岁的身高统计图？请说明判断的理由。

问题三：推测小婷接下来一直到老时的身高变化情况。

生：儿童时期会一直生长，青年时期保持不变，老年时期会有所下降。

师：这也是人类生长的一般规律。

三、回顾反思（略）