教材中定义新数试题素材新探——基于6 174黑洞数的试题编制

张 豪 张维忠

(浙江师范大学教育学院 321004)

《义务教育数学课程标准(2022年版)》强调试题命制不仅要坚持素养立意,凸显育人导向,注重应用性、探究性和综合性试题的编制,更重要的是需要设置合理问题考查学生的思维过程,让学生经历数学学习的运用和实践探究质疑的经验积累过程[1]．纵观近几年全国各地中考试题,新定义试题凭借背景新颖、解法多元、考查深入等特点逐渐成为中考的热门题型．其中,定义新数这一类型的试题以初中核心知识为载体,以新概念作为思维的出发点、增长点与突破点,以基本思想为手段,以数学思考为导引,对于触动学生深层思维思考至关重要[2]．但定义新数试题究竟新在何处,如何才能触动学生深层思考?

1 定义新数试题触动深层思考的关键:合适的问题梯度与合理的开放空间

在数学课程中,学生往往被期待要领会比教材本身更多的数学．推理训练这一途径通过学生接触并解决难度日益增加的问题能够达到这一目标．事实上,定义新数试题恰源于教材又高于教材,意在通过类比、引申或拓展给出新数概念,让学生通过阅读理解明晰定义本质从而解决难度日益增加的问题,深度考查学生概括、思辨等推理能力[3]．

2013年成都中考的本位数、2017年长沙中考的和谐数、2020年常州中考的特征数……随着近年来数学中考定义新数试题的不断涌现和命题探索,定义新数试题不仅素材逐渐丰富,而且在推动学生对试题进行深度思考方面不断深入．这些学生不熟知的情景是新颖、公平且具有挑战性的,需要学生深入理解定义并挖掘关键条件和本质,旨在让学生通过推理解决问题,引发深度思考．然而部分定义新数试题依旧停留在依葫芦画瓢的表面应用,究其原因在于缺乏合适的问题梯度与合理的开放空间,没有触及新数被定义背后蕴含的数学思想方法,难以触动学生深层的理性思考．

例1(2019年重庆数学中考第22题)现在我们来研究一种特殊的自然数——“纯数”．定义:对于自然数n,在计算n+(n+1)+(n+2)时,各数位都不产生进位,则称这个自然数n为“纯数”．

(1)判断2 019和2 020是否是“纯数”,请说明理由;

(2)求不大于100的“纯数”的个数．

从(1)(2)两问的解决过程入手可以发现,被创造出来的纯数的定义只是为了让学生依据性质进行计算的套用,做题方向明确且不会给学生带来思维切入的束手无策,属于定义新数试题思维开放空间不够深入的一个实例．但若我们针对第(2)问进行改编,将问题设置改为“列出不大于100的纯数,简述一下你是如何快速判断这些数是纯数的”,就将题目原本依葫芦画瓢的重心转移到了如何判断100之内的数为纯数的思想方法角度上来,尤其是题目中简述的要求大大增加了题目的开放性,促使学生对本题进行思维层面的深度思考．

例2若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”．如3=22-12,7=42-32,8=32-12,因此3,7,8都是智慧数．

(1)18智慧数,2 017智慧数.(填“是”或者“不是”)

(2)除1外的正奇数一定是智慧数吗?说明理由．

从(1)(2)两问的设置来看,对2 017是否为智慧数的判断,其实是除1外的正奇数一定是智慧数的一种特例．但是对学生来讲,直接从定义的角度猜想2 017是不是两个正整数的平方差、是哪两个正整数的平方差太具挑战性．若是先将第(2)小问提前,则更能引导学生用已知的完全平方公式(n+1)2=n2+2n+1去表示2n+1这一奇数通项,去确定除1外的正奇数一定是智慧数,但这也就缺少了一个特殊的正奇数为智慧数的直观实例感受．由此可见,定义新数试题需设置合适的问题梯度,为学生挖掘新数背后的数学思想方法提供良好工具,避免学生无所适从．

例3(1990年北京市竞赛卷)一个非零自然数若能表示为两个非零自然数的平方差,则称这个自然数为“智慧数”,比如16=52-32,故16是一个“智慧数”．在自然数列中,从1开始起,第 1 990个“智慧数”是.

例3通过“第1 990个智慧数是什么”的提问设置了极大的开放空间,蕴含分类讨论的数学思想,旨在让学生摸透智慧数的定义本质．突破本题的关键在于明确如何在自然数列中选择数成为智慧数．结合定义我们可以发现判断一个数是否为智慧数,关键在于这个数能否写成两个非零自然数的和与差的乘积的形式,抓牢(n+1)2-n2=2n+1,(n+1)2-(n-1)2=4n这些特殊的平方计算公式,不难发现每个大于1的奇数和每个大于4且是4的倍数的偶数都是智慧数．基于此,从奇数智慧数与偶数智慧数的特征入手,就可以求得第1 990个智慧数．

结合例2、例3来看,对于智慧数问题的编制,1990年北京市竞赛卷更加能触动学生的深层思考,但要求学生直接从奇数与偶数中确定智慧数的特征太具挑战性．如若站在“除1外的正奇数一定是智慧数吗?说明理由”的开放性问题基础上设置新的问题阶梯,则可更快、更准确地触动学生思维．将例3的问题设置改为:

(1)除1外的正奇数一定是智慧数吗?说明理由．

(2)在自然数列中,从1开始起,第1 990个“智慧数”是.

(3)在自然数列中,从1开始起,第k个“智慧数”是.

这样的编制不仅保留了例2中的开放性问题的启发作用,更是在正奇数的规律展示后,将例3求第1 990个智慧数的思维方法一般化,要求学生更深层次地回归本质理解该题,更能触动学生思维的活跃性．

综上可见,设置合适的问题梯度、合理的开放空间对促进定义新数试题更好地触动学生的深层思维、展现试题的育人功能至关重要．

2 一道定义新数试题实例编制构思:新探课本素材和挖掘思想方法

定义新数试题虽然呈现了新的形式和概念,但是透过概念本质发现其仍旧是与教材上的知识密切关联的,比如智慧数的概念就与平方公式息息相关．那么教材在介绍有理数、实数这些与数有关的章节知识时,是否早已暗藏了一些“新数”的影子?由此,笔者再次回归教材重新探寻课本素材并深入挖掘思想方法,以下呈现一道定义新数试题的编制的心路历程．

·新探课本素材

北师大版七年级上册数学教材在第二章《有理数及其运算》习题2.17问题解决部分有这样一道题:写出一个四位数,它的各个数位上的数字都不相等(如6 731)．用这个四位数各个数位上的数字组成一个最大数和一个最小数,并用最大数减去最小数,得到一个新四位数．对于得到的新四位数,重复上面的过程,又得到一个新四位数．一直重复下去,你发现了什么?请借助计算器帮助你进行探索．

浙江教育出版社《数学作业本(七年级上)》(2021年版)第18页第7题也类似地让学生利用计算器,按照流程图(图1)操作并猜想规律．

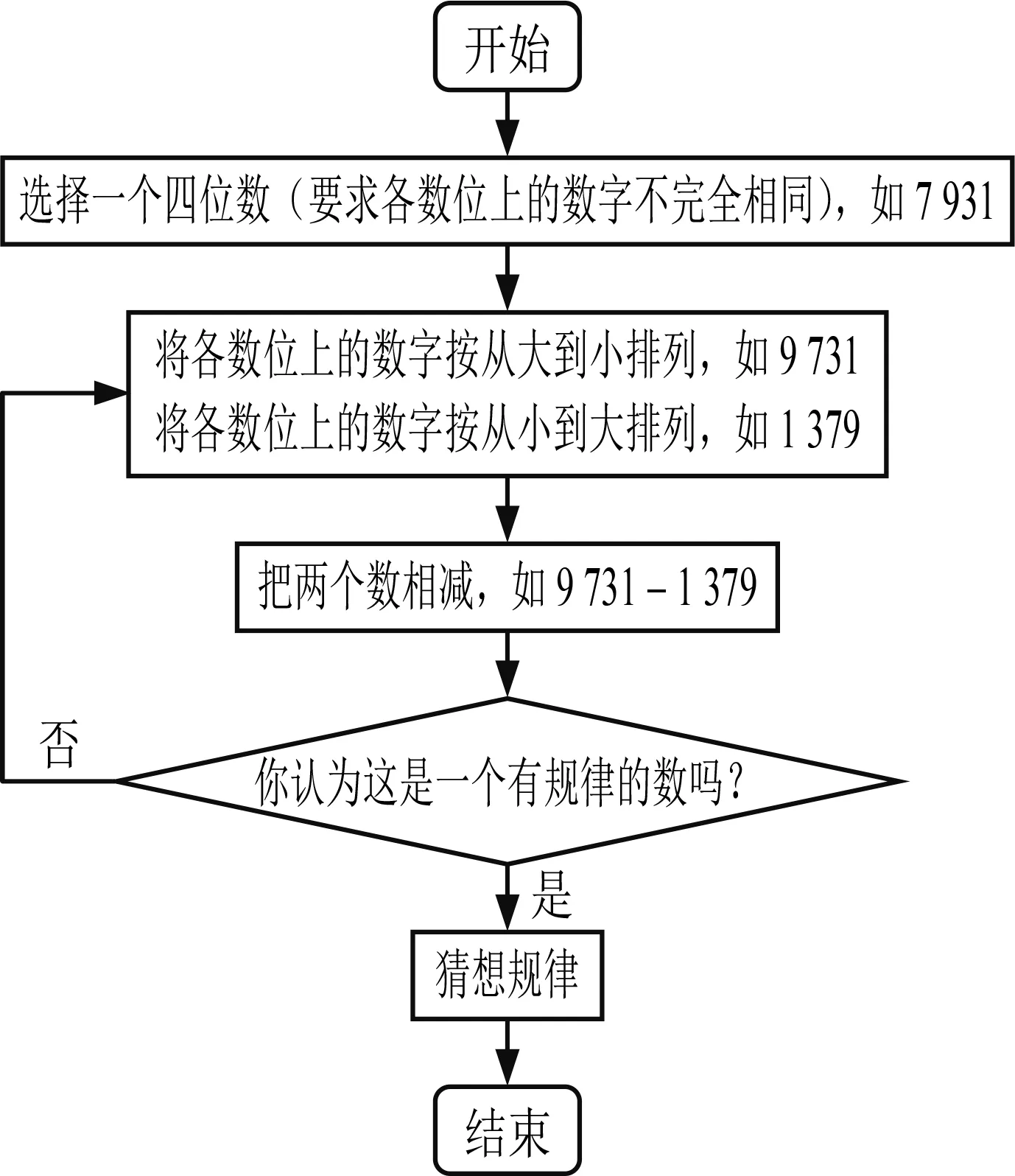
图1

这两道题都意在让学生利用计算器来验证一个特殊的性质:任意数字不全相等的四位数,经过“由这四位数的四个位数的数字组成最大数减去最小数的差”的反复运算,在有限步(7步)之内必得出6 174,随后运算结果均为6 174．这个神奇的数最早由印度数学家卡普雷卡尔发现,也曾被称作马丁猜想．但仅仅利用计算器进行验算并不能在习题所呈现的思想方法层面进行深度挖掘,究竟为何各数位不全相等的四位数会掉入6 174的循环陷阱这一问题背后的思想方法才是宝藏与精华所在,这为围绕6 174这一循环的“黑洞数”进行试题编制、触动初中学生深层数学思维提供了极大空间与可能．

·挖掘思想方法

由于这个问题仅涉及9 990个四位数(包括有0在千位的情况)[4],显然可以借助技术手段通过枚举的方法验证这个猜想,但这就缺少了这道题用于启发学生思维的灵魂所在．那么不借助技术手段,可以通过哪些方法直接将其背后所蕴含的数学思想方法传递给初中生?结合已有研究,可以采取以下两种方法突破:

方法1 蒋荣清[4]将组成这个四位数的四个数字设为a,b,c,d,且a≥b≥c≥d(a,b,c,d不全相同),则经过一次运算得到的新四位数k1=1 000a+100b+10c+d-1 000d-100c-10b-a=999(a-d)+90(b-c)的取值仅与(a-d),(b-c)的取值有关,共有54个．在这54个四位数中,又有一部分数在组成四位数的数字上相同,可归为同类数．因此只需对剩下的30个同类数进行逐一验证即可．

可见,对于6 174黑洞数的发现和证明方法蕴含着宝贵的思想财富,倘若能将其转化为定义新数试题,通过设置合适的问题梯度与合理的开放空间让学生进行自主探索,则学生在思维方面将受益无穷．

3 黑洞数的试题编制及其教学思考:融会思想方法和触动深层思考

编题16 174这一神奇的四位数被称为“黑洞数”,因为对于任意一个各个数位上的数字不全相等的四位数,我们将这个四位数各个数位上的数字组成一个最大数减去它们组成的一个最小数,得到一个新的四位数,再重复这个步骤,总能在7次运算之内得到6 174．

(1)用6 174,6 731,8 964这三个四位数进行上述运算,分别需要几次才能得到6 174?

(2)我们将组成任意一个四位数的四个数字设为a,b,c,d,且a≥b≥c≥d(a,b,c,d不全相同),观察发现进行一次运算后得到的新四位数的取值与a,b,c,d存在什么联系,有几种取值可能?

(3)在(2)的基础上,经过一次运算得到的这几种四位数在数的组成上存在什么共同特点?谈谈你的发现．

编题1的设问意在将蒋荣清对黑洞数证明的思想方法巧妙地融入试题让学生进行探究．首先,第(1)问旨在让学生经过实践,发现6 174经过1步运算即陷入循环,6 731,8 964则分别经过3步、7步陷入循环,让学生直观感受到6 174黑洞数的神奇．第(2)问在题干部分先完成对四位数的设元,旨在让学生从一般结构入手探究6 174为何能成为黑洞数,“得到的新四位数的取值与a,b,c,d存在什么联系”的询问意在让学生发现新四位数的取值仅与(a-d),(b-c)的取值有关,从而确定对9 990个四位数的黑洞性质研究只需转化为对54个特殊的四位数的研究．第(3)问则留下了更大的思考空间,通过询问经过一次运算后所得四位数的组成特点,旨在让学生发现第(2)问转化的54个特殊四位数研究的“同类性”——即在数位组成上4个数相同的四位数,再经过一次运算后得到的四位数相同．

从整个题目上看,小题设置上让学生先经过运算切身体验黑洞数的循环性,再从一般的代数角度设元思考,然后让学生总结发现四位数的运算规律,深度考查设元、分类、归纳等思想．教师针对此题进行教学时,不仅可以让学生直观感受数学中考定义新数难题的课本来源及其变形过程,强调其本质——思想方法的内核,还能通过仅用30个同类数完成替代9 990个四位数的证明,达到潜移默化传递数学简洁美、形式美的效果．

编题2对于任意一个各个数位上的数字都不相等的四位数,我们用这个四位数各个数位上的数字组成一个最大数减去它们组成的一个最小数,得到一个新的四位数,重复这个步骤,若能在有限次运算之内得到一个重复循环出现的四位数,就把这个神奇的四位数称为“黑洞数”,那么黑洞数有几个?具体数值又是多少呢?

编题2的设问将孙传龙等对于黑洞数猜想的代换思想首先进行简单的阐述,再灵活地融入试题让学生进行探究．题干讲清楚了寻找黑洞数的初等数学方法,保留了开放空间让学生自行寻找并验证a-d,b-c-1,10+c-1-b,10+d-a与a,b,c,d分别相等的多种可能性,留下了足够的探索空间让学生去验证当且仅当a-d=b,b-c-1=d,10+c-1-b=a,10+d-a=c时,黑洞数有唯一解,为6 174．

此题分类情况复杂,如何选取一个合适的分类标准并进行验证对学生来说是一大难点,但解题方向十分明确,学生对分类情况的处理也能够体现思维的深度．虽然这道题涉及四元一次方程组及其解法,属超纲知识,但是站在消元的思想方法角度上,其本质与三元一次方程组一致,且未知数的系数均为±1,计算消元处理不难．教师可以将其作为三元一次方程组及其解法的拓展练习,在验证消元水平能力的同时深度考查学生的分类讨论思想应用能力．