跨学科情境教学:数学课堂的项目化改造——以“孟德尔遗传规律”的教学为例*

张 洁 戴小驹 黄 丽

(江苏省苏州工业园区星海实验中学 212028)

1 数学项目学习

数学项目学习是以数学核心知识为载体,学生通过探究性学习等数学学习实践,对真实、具有挑战性的驱动问题进行探究,运用问题解决等高阶认知策略,创造性地解决问题,形成公开成果,提升数学核心素养,促进深度学习的学习模式．[1]数学项目化学习的实施需要天时、地利、人和,既要关注初中生的认知特点,也要教师“适逢其时”地进行引导与点拨．数学项目化学习是“数学”的,体会、运用数学与其他学科之间的联系,旨在提高学生学习数学“悟”的能力．

2 数学项目学习设计

本课题以苏科版《数学(九年级上册)》“阅读与思考”中的“孟德尔遗传规律”作为真实情境中的问题进行思考．为了能够研究出豌豆杂交实验的结果,需要结合跨学科生物知识,搭建数学模型,并结合计算机和大数定律,研究出豌豆杂交结果子一代、子二代、子三代花色的概率．

“孟德尔遗传规律”是一个生物学的知识探究,“孟德尔遗传规律”数学项目化改造则是数学研究的综合性项目,本课的学习可促进学生综合核心素养能力的提升．

2.1 项目学习目标

本课程的目标设计如下:(1)通过查阅文献资料、使用互联网查询等,认识遗传定律相关知识;(2)通过“孟德尔遗传规律”进一步理解书本频率与概率的关系,说清楚“孟德尔遗传规律”遗传机理概率模型;(3)通过跨学科知识的渗透充分感受概率与其他学科的紧密联系,经历数学概率模型建构的过程,提升数学建模能力．

2.2 项目学习内容

项目式学习是一种以真实问题为起点,以取得项目成果为目标,以知识运用、能力提升为导向的学习模式．对于遗传学中“孟德尔遗传规律”的基因杂交试验,项目小组对其采取模拟试验,寻找对应的“替代物”进行多次试验,绘出频率估计概率折线图,并根据频率折线图采用计算机编程绘图整理,最终得出“孟德尔遗传定律”的遗传现象．医学界对“孟德尔遗传定律”的应用尤其广泛,根据此定律可推算出某些遗传病患者的概率．

概率统计是应用性非常强的内容,如何将数学知识应用到其他学科乃至生产生活中显得尤为重要．因此,本课程项目的教学难点是:如何将生物学实际问题转化为概率问题．

本项目课程在学生小组活动过程中引导学生在跨学科“孟德尔遗传规律”情境中发现问题、解决问题,并在此过程中发现新的问题与探索问题的思路．项目设计内容如图1所示．

图1

学生小组合作探索“孟德尔遗传规律”的数学原理,最终形成“孟德尔遗传规律”生物学中不常见的排列组合数学原理．在项目化学习过程中,教会学生用数学的眼光观察世界,并用数学的已有知识修正、完善自己的作品,提升自我学习、反思与总结的能力．

3 数学课堂项目化教学过程

本项目课程采用跨学科情境教学,具体学习过程如图2所示．

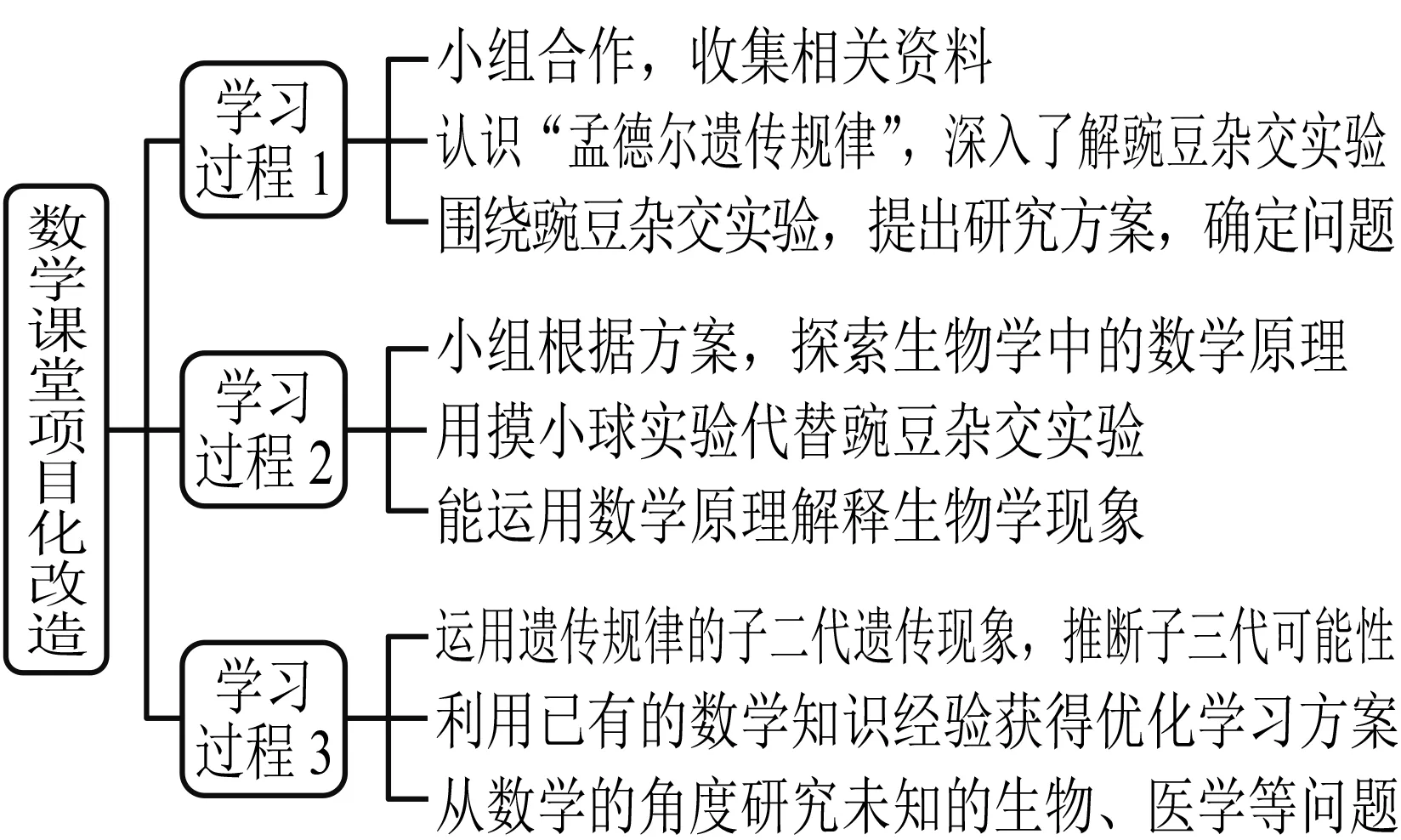
图2

对于项目学习过程1,学生收集孟德尔遗传规律相关资料,认识了孟德尔遗传规律的相关知识,并提出了相关的实验问题:(1)豌豆杂交实验是否有相关的替代物进行模拟实验?(2)模拟豌豆杂交实验,怎样确保实验的可能性相等? (3)对于某个随机现象,如果我们先提出一个理论概率模型,如何对模型的正确性进行验证? (4)当从所有子二代豌豆中随机选择豌豆进行交配时,结合数学概率知识,子三代豌豆的花色比值是多少?根据这几个问题,学生查阅资料进行项目化学习,但只是对孟德尔遗传规律的浅层认识,并没有深入学习．

以下是项目学习过程2的数学课堂,即数学课堂的项目化改造教学实践:

情境引入 学生在看到食堂的番茄颜色时,议论到这与生物知识有关．这看似是一个生物学的问题,数学老师觉得这与我们的数学知识息息相关,于是,项目学习小组开始了相关探索．

3.1 类比分析,形成原理

活动1 数学课堂项目化改造——生物与数学的联系．

问题1对于生活中的遗传现象,小组搜集到与遗传有关的知识有哪些?

第1组学生上台展示项目学习的前期准备:达尔文进化论、孟德尔遗传规律．这两位生物学家对生命与遗传所作出的贡献及其不同之处．

活动预设 学生分组讨论,总结自己的项目活动知识,用自己的语言描述生物学与数学的联系,教师适当完善．

设计意图通过生物学中孟德尔遗传规律和初中数学中的概率相关知识类比分析,帮助学生厘清内在联系．

活动2 数学课堂项目化改造1——亲代选种项目试验．

问题2根据历史记载,第一代开白花的纯种与开红花的纯种彼此授粉,第二代豌豆花会出现粉色花朵．到第三代,粉色花朵的数量会增加(呈现苏科版《数学(九年级上册)》“阅读材料”——概率帮你解释实验数据[2])．假设豌豆花的颜色为WW(白),RR(红),即一种颜色由两个基因决定．

既然孟德尔遗传规律与数学中的概率有着如此多的联系,在数学学习中学生自然会想到模拟孟德尔豌豆花实验,因此教师提出以下问题:

问题3根据以上阅读材料,你们能在生活中找出可以替代豌豆基因WW,RR的物体吗?怎样可以确保它们机会均等?

活动预设 做摇小球抽奖游戏:准备一个摇小球摸奖机,每个摸奖机内放入两个小球,为了接近于生物实验,选取的小球一个红色(RR)、一个白色(WW)．每组选三名学生,一名学生负责摇小球,一名学生负责记录次数,第三名学生记录小球颜色．为了在有限的时间内获得更多的数据,全班分成多组进行实验,最后将实验结果累加得到较大的数据．操作活动后,回答问题．

设计意图通过学生小组做游戏,让学生初步认识孟德尔遗传规律与概率的潜在联系．对于亲代选种实验,研究内容简单,摇小球实验中只出现两个小球．本课题选取的七年级学生小组对本次实验研究兴趣浓厚．

通过课堂上定时的实验,每小组的实验次数有限,小组长汇报出的数据偏差较大,并没有得出亲代选种1∶1的概率结果．

项目小组课前进行较充分的准备,第2小组进行抛掷硬币2 000次试验,第3小组进行摇小球2 000次试验．每次摇出小球后再放回是为了保证下次摇小球时摇出红色(RR)与白色(WW)小球的概率相等．

通过两组的项目准备,对本小组的试验结果进行整理,绘制成统计折线图(图略)．

引出思考:项目小组课前准备的两种试验数据是否可以累加?答案是肯定的．第4小组代表对两组同学的数据进行了整合(图略)．

问题4对于项目实施过程的第一阶段,在孟德尔遗传规律中,选种试验依据什么猜想事件A(豌豆花是红色花)发生的概率为0.5?对于这个亲代选种试验,我们如何对模型的正确性进行验证?

活动预设 学生结合阅读材料与已有经验可以推断此选种试验结果接近于0.5,那么对于大数定律,为了验证这个结果的正确性,第5小组进行计算机编程,得出模拟程序(图略),能够以大数据模拟该生物选种试验．

设计意图计算机模拟程序是数学建模的一种方式．七年级学生在生物学、计算机编程与数学相融合的综合实践中,探索出相应的项目试验结果,从而提升学生的综合素养能力．

3.2 创建模型,模拟试验

活动3 数学课堂项目化改造2——子一代杂交项目试验．

问题5根据前面小组的选种试验,我们发现WW,RR被选种的概率分别为0.5．如果亲代选取WW,RR进行杂交,那么杂交结果是什么颜色?概率是多少?

设计意图本活动由学生根据已有经验回答,即杂交结果一定是粉色,并得出概率中“必然事件”的概念．

活动4 数学课堂项目化改造3——子二代杂交项目试验．

问题6根据史料记载,亲代纯种WW,RR豌豆花杂交一定得到WR(粉红)子一代,如果选取WR(粉红)、WR(粉红)进行杂交试验,那么我们如何选取模拟试验材料?同学们如何选取该模型的替代物?

活动预设 学生选取摸小球试验的原因是摸小球试验可以保证摸出的小球是等可能的．每次摸出小球后需要再放回,是为了保证在下次摸小球时,摸出W和R的概率都是0.5．如果利用大量的子一代进行杂交试验,子一代携带基因的概率也是相等的．

数学课堂上增添了跨学科知识,学生在收集资料的同时也咨询生物及计算机老师,注重科学的严谨性．学生查阅资料发现子二代杂交结果数据是:红色∶粉色∶白色=1∶2∶1．由于课堂时间有限,各小组并没有得出相关比值,可能的原因是统计数据较少．

第6小组对摸小球试验进行了上千次试验,得出相关数据折线图(图3)．

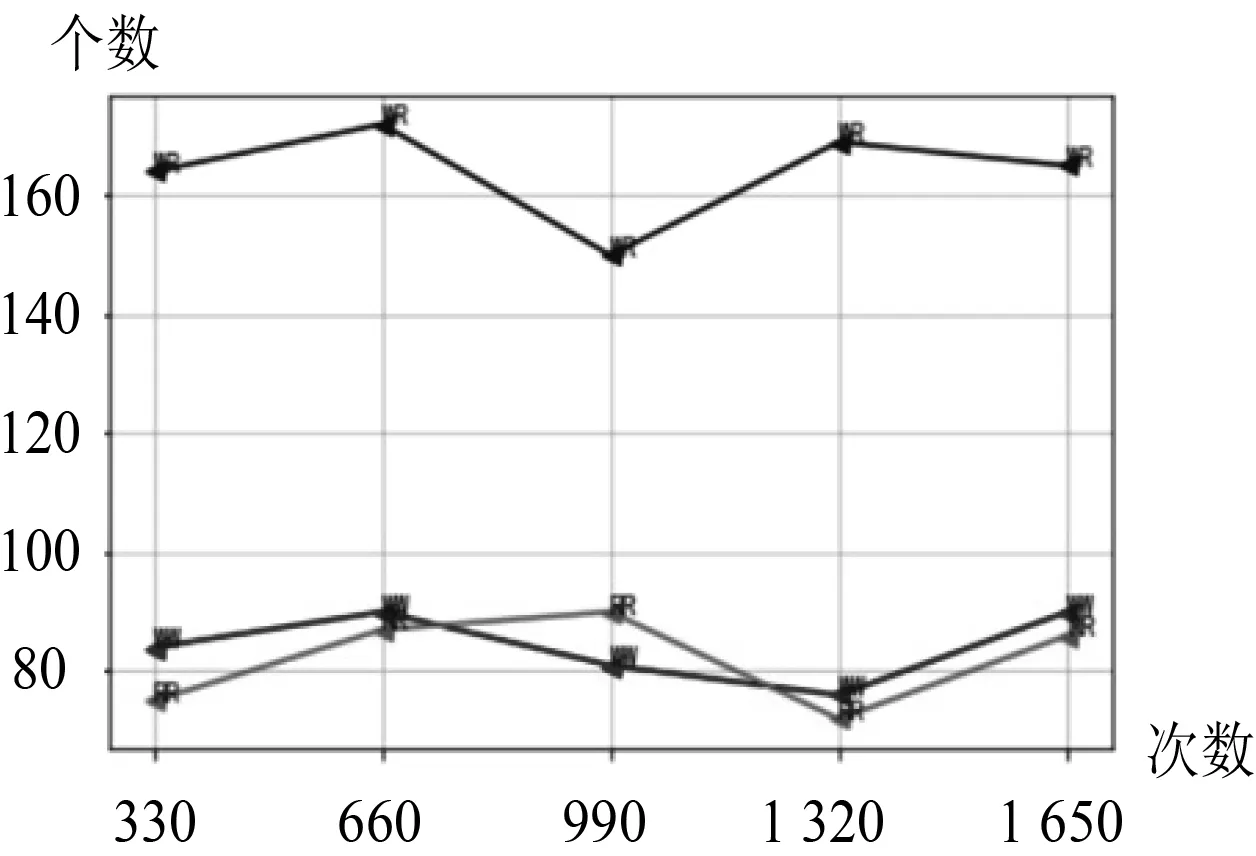
图3 染色体为WW的概率

设计意图提出一个理论模型后,小组通过试验统计这些事件实际发生的概率．如果实际的频率稳定在预测的概率附近,那么模型就是正确的;反之,则模型出现错误．

问题7大数定律阐述了随着试验次数的增加,频率稳定在概率附近．孟德尔就是根据大数定律,结合事件发生的概率,构造出遗传机理概率模型．那同学们知道这几个事件发生的概率是多少吗?

活动预设 为了验证模型的正确性,第5小组仍然对此进行了计算机大数据模拟试验,并得出相关的豌豆花颜色的数量比例是:红色∶粉色∶白色=1∶2∶1(程序略)．

问题8我们现在验证了孟德尔遗传定律的模型,并发现我们预测的事件概率是正确的．你能用数学语言来描述子二代的杂交试验吗?

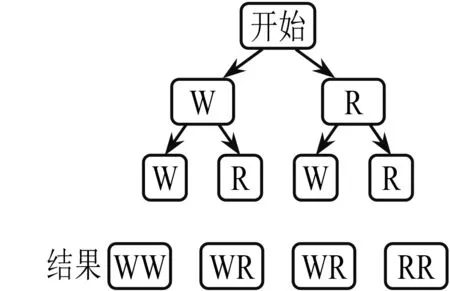
图4 概率树状图

活动预设 学生对大数定律的猜想——验证孟德尔遗传规律的正确性,根据教师的现场指导,经过改进,得出数学概率树状图(图4)．

设计意图学生对孟德尔遗传规律进一步理解与研究．通过跨学科知识的渗透,学生理解数学概率知识的内涵．通过大数定律验证孟德尔遗传规律的正确性,之后的问题9是学生用数学的思维方法,在真实的科学技术情境中,有逻辑地分析问题;用数学的语言,将生物学中孟德尔遗传规律转化为数学问题,感悟数学与生物学的融合,逐步形成“会用数学的思维思考现实世界”的核心素养．

3.3 项目改造,推理结论

活动5 数学课堂项目化改造4——子三代自交、杂交项目数学验证．

问题9据教科书中的子二代杂交结果,可知豌豆花颜色的数量比例是:红色∶粉色∶白色=1∶2∶1,那么子三代会出现怎样的情况?

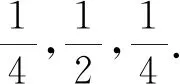
根据以上项目化改造后的教学课堂,推理得出数学与生物学的相关结论．学生收集整理孟德尔遗传定律,并发现生物学中提到的自然状态下,不可能出现百花齐放．

设计意图由生物跨学科情境转化为数学问题,模拟豌豆杂交试验向数学抽象过渡,给学生充足的思考时间和交流空间．通过学生思考、分组讨论的方式不断探索,让学生能够自然而然地得到数学结论,使教师启发和引导课堂策略得到充分体现．

4 数学课堂项目化教学评价

本节课,以孟德尔遗传规律作为项目学习的展示汇报课,是数学课堂的项目化改造．从跨学科知识孟德尔遗传规律项目情境入手,精心设计问题串,将项目实施过程串联．学生的项目合作形成教学评价表,如表1所示．

表1 学生项目学习活动评价表

5 教学反思

5.1 夯实学科基础,凸显活动预设

学生的数学学习起点往往不是逻辑公理,而是生活中的一些实际案例．学生认识和学习数学的过程是对现实经验的理解与反思过程[3]．数学在其他学科上的应用非常广泛,培养学生学习数学的能力显得尤为重要．数学项目活动创设情境时,要挖掘数学的人文价值与与人价值．

正如本项目提到的孟德尔遗传规律的数学项目化教学过程,数学学科也是学好其他相关学科的基础．正所谓“十年苦修,一朝得道”,扎实打好数学学科学习的基础,以平常心对待,在“非教非授”之间营造“感知悟之”的学习环境,凸显数学课堂的活动,使学生最终掌握学习的能力．

5.2 构建逻辑过程,强化数学建模

跨学科主题学习要立足于数学课程学习中核心知识和关键能力的应用．本项目课例选取生物学跨学科主题,贴近学生的现实生活,聚焦豌豆花颜色这个真实问题的解决,实现数学与生物学的有机融合．

本项目将孟德尔遗传规律中的豌豆花试验与数学中的摸小球试验进行拟合,对生物学的试验构建逻辑过程,并把此项试验进行数学建模,然后采用现代计算机技术进行大数据拟合试验,以取得更精确的试验结果．学生在数学建模过程中能够主动探索数学与生物学知识,并且在探究问题时实现数学知识与跨学科知识的融合,达成教学目标,提升学生探究能力．

5.3 创造自由环境,改造数学课堂

数学是一池活水,项目学习教学让数学这一池活水变得更为灵动．本项目用概率方法解决现实的孟德尔遗传规律问题,引导学生发现、解决现实中的遗传问题．教师制定合理的解决方案,学生经历发现问题、提出问题、分析问题和解决问题的过程．通过项目化改造,数学课堂不再是重结果轻过程的传统模式,而是在自由、创造的思维中不断改进．

数学课堂教学的成功有赖于教师的不断实践,也就是说,我们教师应通过“苦修、乐修、真修、共修、自修”的方式参与到数学课堂的项目化实践中,把数学课堂的项目化实践看成是专业成长的机遇．长此以往,必定有成果．