中国古代数学的图腾:赵爽弦图

张维忠 唐慧荣

(浙江师范大学教育学院 321004)

大家一定都听过“大禹治水”的故事吧．“大禹治水十三载,三过家门而不入．”家喻户晓的他是如何成功治水的呢?赵爽在《周髀算经注》中这样提到:“禹治洪水,决流江河.望山川之形,定高下之势.除滔天之灾,释昏垫之厄,使东注于海,而无浸溺.乃勾股之所由生也．”大禹治水竟然与著名的勾股定理有关,是不是有些出人意料呢?

一直以来,勾股定理作为“千古第一定理”,是浩瀚无垠的数学海洋中不可缺失的一颗耀眼明珠,在几何学科中举足轻重．它的神秘面纱吸引了广大的数学爱好者,不同的民族对其都有着独特的探索．目前,世人对其证明的方法已达500多种．在我国,那不得不提及的就是著名的“赵爽弦图”．赵爽到底是如何证明勾股定理的呢?下面,我们一起来探究华夏文明中这颗几何学的璀璨明珠——赵爽弦图．

1 什么是“赵爽弦图”

1.1 中国勾股定理的最早记载——《周髀算经》

在中国古代,人们把手臂弯曲成一个近似直角时,靠近肩膀的那部分就叫做“勾”,靠近手的那部分便叫做“股”．一般来说,“勾”的长度小于“股”的长度．西周初年,商高在与周公旦的对话中提到“勾广三,股修四,径隅五”．后人简单地称之为“勾三股四弦五”,这便是“勾股定理”的雏形．它如何产生的呢?

大约在4 000多年前,黄河流域洪水为患,汹涌的洪水淹没了田地和房屋,百姓苦不堪言,部落治水九年却得不到成效．善良的大禹不忍看到百姓饱受水害之苦,他吸取前人的经验,利用“左准绳,右规矩”进行测量,走遍了山山水水,终于治水成功!咆哮的河水失去了以往的凶恶,百姓的日子变得安定．大禹在此所用的“准绳”和“规矩”就是我国最早的测量工具．简单地说,准绳是定平、画直线的工具,可以用来检测水平和垂直．规矩则分别用来画圆形和方形．

图1 《周髀算经》书影

大禹是如何利用这两个工具的呢?《周髀算经》(图1)中提到,大禹是利用了“勾广三,股修四,径隅五”(32+42=52)的原理来进行距离的计算、规划并划分九州以达到疏通河道的目的的[1]．

对于32+42=52,这是勾股定理的一个特例,也是勾股定理在中国的最早记载．追根溯源,勾股定理是我国古代数学发展的重要起源,中华数学传统中的精髓开方术、方程术等都与勾股定理密切相关．我们知道,数学是一门严谨的科学,任何结论的提出都必须经过一步步的逻辑推理．因此,定理的发现是一回事,但对其进行严格的证明更是一件了不起的事．千百年来,人们被它的魅力吸引,对此定理的证明趋之若鹜．目前,它是世界上已知证明方法最多的数学定理之一,但在《周髀算经》中尚未发现直接的相关证明．

1.2 中国数学界的图腾——赵爽弦图

我国最早对勾股定理进行证明的是三国时代的赵爽(约182—250)．赵爽是我国三国时代的数学家、天文学家．早在公元3世纪左右,他在为《周髀算经》作注释时,便撰写了《勾股圆方图说》一文,介绍了“勾股圆方图”(图2)．这幅图也就是著名的“赵爽弦图”(图3)．

图2 勾股圆方图 图3 赵爽弦图

图4 第24届国际数学家大会会标

“赵爽弦图”被人们称为“中国古代数学的图腾”,它简约美观而不失深厚,是数形结合思想的典型体现．图形呈中心对称,内部是由4个全等直角三角形围着一个小正方形形成,外部则是将这4个三角形的顶点连接成一个大正方形．一直以来,“赵爽弦图”在数学人心中的地位非同小可．我国著名数学家华罗庚曾建议用一幅反映勾股定理的数形关系图来作为与“外星人”交谈的语言．2002年第24届国际数学家大会会标(图4)就依此制作．让我们想象一下,这个古老而饱含智慧的图案是不是还像一个转动着的风车?它透露着中国人民热情友好的民族特色[2]．

那赵爽是如何记载的呢?他在《周髀算经注》中写道:“勾、股各自乘,并之为弦实.开方除之,即弦．”你们能看懂这句古文的意思吗?

这样来看赵爽所记载的内容就是大家所熟悉的勾股定理“原貌”.在初中教材中,一般把勾股定理简单表述为:直角三角形两直角边的平方和等于斜边的平方．

作为一条古老的数学定理,勾股定理包含着中国古代厚重的文明,它的出现和发展对于发扬古代数学文化起到了重要作用．纵观数学史,它不仅为几何学奠定了基础,它衍生的许多分支也都得到了广泛的应用,对数学学科的发展有着深远的影响．比如,在中学数学学习中“利用数形结合,把直角三角形的特征转化成三边的数量关系”,勾股定理就与之密切相关．

2 赵爽弦图与勾股定理

对于利用赵爽弦图来证明勾股定理,目前有两种比较主流的方法:一种是数学史家钱宝琮(1892—1974)解读的“代数证明”,另一种是数学史家李文林提出的“出入相补”[3]．

2.1 “赵爽弦图”与“代数证明”

我们跟着钱宝琮先生一起来解读赵爽弦图吧．

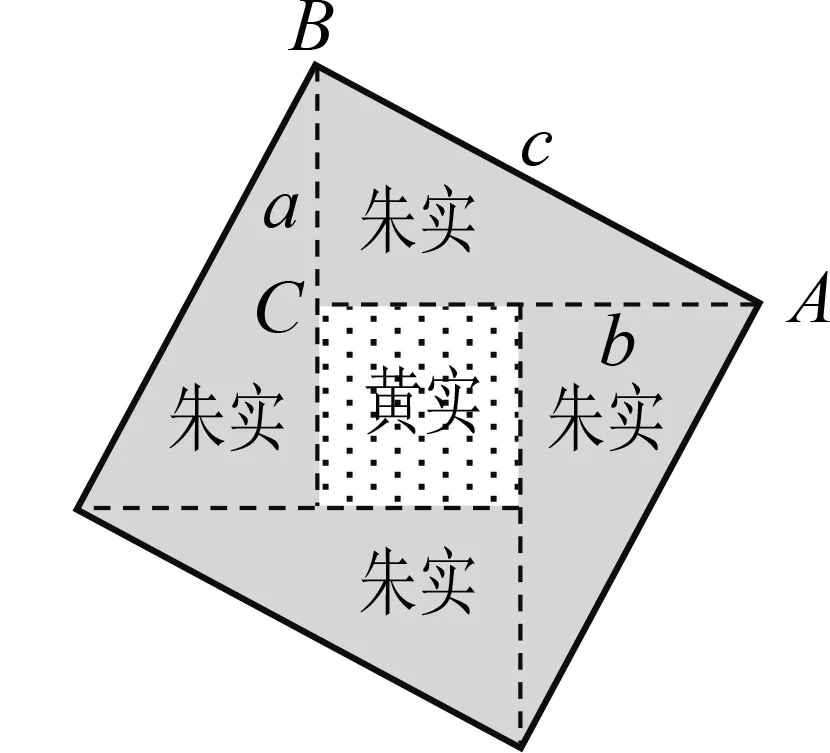
图5 弦图

观察弦图(图5),图中的4个全等直角三角形涂上了朱色,其面积被称为朱实;中间的1个小正形涂上黄色,其面积被称中黄实．赵爽写道:“按弦图,又可以勾、股相乘为朱实二,倍之,为朱实四.以勾、股之差自相乘,为中黄实.加差实,亦成弦实．”

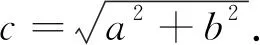
值得指出的是,在弦图原图中,虽然赵爽画的是边长为3,4,5的直角三角形,但其证明不失一般性,可见古代中国在数学上的成就不同凡响．

2.2 “赵爽弦图”与“出入相补”

数学史家李文林认为,赵爽是利用了“出入相补”的原理来证明勾股定理的．“出入相补”原理,顾名思义,就是对图形进行分割再移补而解决问题的方法．对此,有没有似曾相识的感觉呢?在平面图形面积计算的教学中,我们就是利用“转化”的数学方法进行公式推导,如将三角形进行分割拼成长方形后进行面积公式的推导,这就是出入相补的应用．

在总面积相等的条件下,先对两个正方形进行分割,根据需要移动补凑,对分割后的图形进行位置上的变动,就这样达到了证明勾股定理的目的．如图6(1),根据一个直角三角形的两条直角边a,b为边长的两个正方形画出的一个合并图形,面积为a2+b2;再如图6(2)这样,截下两个直角边分别为a和b的全等三角形,并且将这两个直角三角形旋转至图6(3),这样就得到一个以原三角形之弦为边的正方形,其面积应为c2．根据变化前后总面积不变,得到a2+b2=c2．在中国传统数学中像这样运用“出入相补”原理证明数学命题的方法十分普遍．

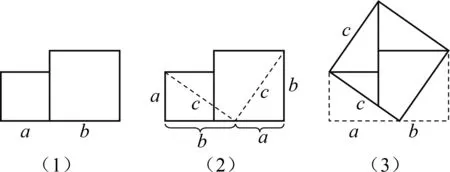
图6

以上两种对赵爽弦图的解读代表了中国古代数学以形证数、数形合一的特点,这种代数与几何之间密不可分的特色在世界数学史上独树一帜．

2.3 穿越古今,感受数形结合的魅力

看了以上的两种证法,如果给你提供以下2个活动材料(图7),你能像古人一样运用自己的智慧感受一下数形结合的证明过程吗?

图7

活动1 探究赵爽弦图的证明

在白纸上先画出图7,再剪下试试．如果碰到困难,可以借助以下三条线索进行解决．

线索1 对比赵爽弦图,利用提供的材料进行拼图实验．

线索2 每一块区域的面积分别怎样表示?它们之间有怎样的关系?

线索3 赵爽弦图还有其他的解读方法吗?你可以利用网络等资源进行了解和探索．

活动2 探究毕达哥拉斯学派的证明

勾股定理作为世界的共同文化遗产,受到了全世界的重视．西方人们相信它是由古希腊思想家、数学家毕达哥拉斯(约前580—约前500)在公元前500年发现的,故称之为“毕达哥拉斯定理”．毕达哥拉斯学派从铺地砖问题中发现勾股定理(图8、图9),但由于学术的秘密性及历史年代的久远,他对勾股定理的证明并没有流传下来．毕达哥拉斯是怎样发现勾股定理,又用了什么方法证明?后人对其做了合乎情理的推测．

图8 图9

请你完成下列任务,试着进行证明．

(1)请仔细观察图10,完成下表．

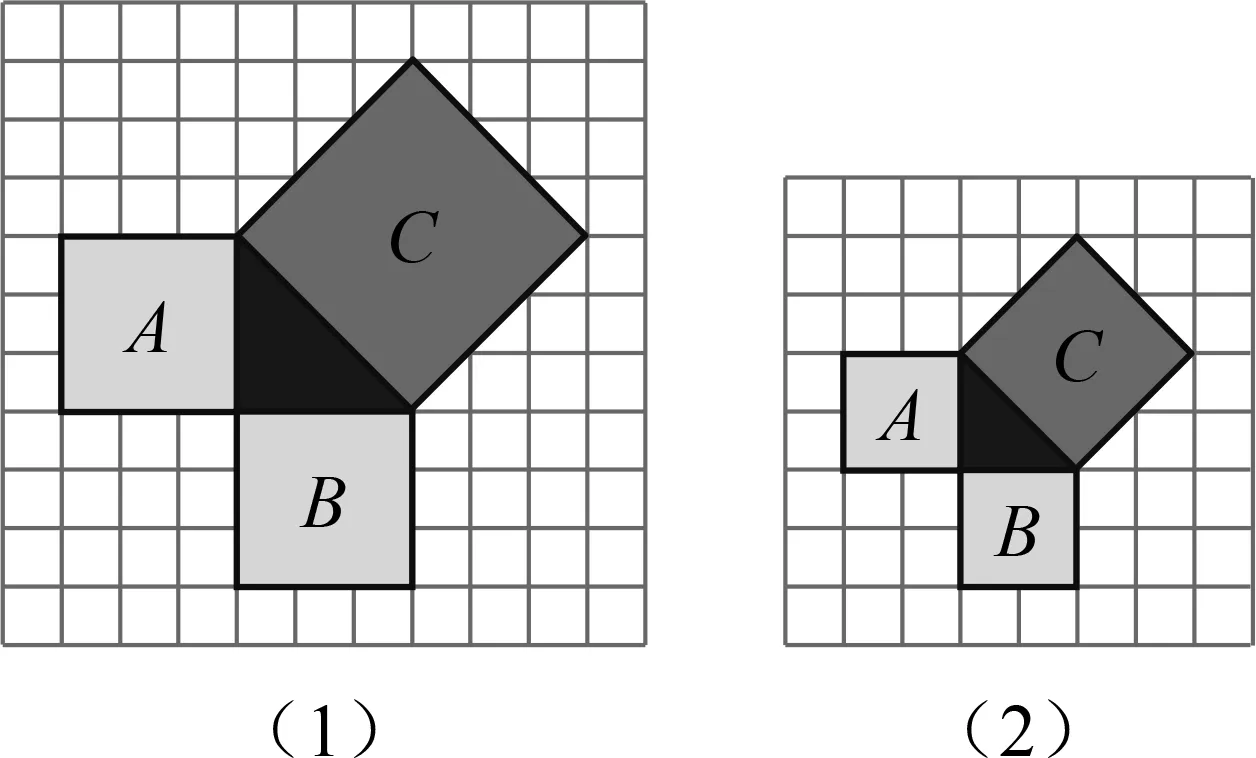
图10

A面积B面积C面积图11(1)图11(2)

(2)你有什么发现呢?

(3)毕达哥拉斯发现了三角形直角边上的两个正方形合起来的面积等于斜边上的大正方形的面积．你同意他的说法吗?

对比两种方法,你更喜欢哪一种?

(待续)