漫谈折纸活动在初中数学教学中的实施

吕小兵

(江苏省江阴市南菁高级中学实验学校 214400)

在“做数学”理念的引领下,围绕数学折纸活动开展的数学实验教学(以下简称“折纸教学”)得到一线教师与专家学者的广泛关注．一般意义而言,折纸教学取材方便,贴近学生生活实际,能让学生动手动脑、开发智力和陶冶情操．然而作为数学教学的折纸活动,如何实现与教学内容有机结合,更好地承载数学学科育人功能,在这个领域仍需要广大教师积极探索．笔者结合教学实践谈一谈自己的理解,抛砖引玉,与读者交流．

1 折纸教学的意蕴

意蕴是指一个事物的内容或意义．折纸看似简单,若从数学的角度加以研究则意蕴深妙,至今已发展出一门被称为折纸几何学的分支．折纸教学中的“纸”一般忽略其颜色、厚度,可以具有一定的初始形状,如三角形、矩形等．“折”是指为了实现某个特定目的所进行的对折操作,折后会在纸上留下折痕．对于折纸的“合法”操作,公认为有以下7种:两点折线、两点对折、两线对折、过点对折、点折到线、双点到线和点线线点[1]．其中前5种可以用尺规作图完成,后2种则因借用了三维空间,使得折纸可以完成尺规作图所不能解决的问题．

折纸教学的意蕴首先体现在对学生数学思维的培养上,通过活动,学生获得手脑协同、启思明理之效．如果教师对折纸教学的意蕴缺乏理解,就会产生活动的目标不明、规则不清、“数学味”不浓、内隐性知识挖掘不充分等表现,造成“纸上得来终觉浅”的观感．

案例1“折”还是“不折”?

在一次公开课中,授课教师对八年级“等腰三角形的性质”一课作出下列教学设计:

(1)课前请学生准备各种不同类型的等腰三角形纸片;

(2)课上请学生将纸片对折,并观察两个底角的关系,归纳出等腰三角形“等边对等角”的性质;

(3)继续观察折痕与底边的关系、折痕与顶角的关系,归纳出等腰三角形“三线合一”的性质;

(4)在归纳出结论之后,尝试进行演绎推理,进而证明等腰三角形的性质定理．

应该说整个教学内容完成得十分顺利,课堂气氛活跃．在阐述设计意图时,该教师认为学生通过折纸进行操作探究,可以直观感知等腰三角形中各种要素之间的联系,进而发展几何直观和逻辑推理能力,感受到成功的乐趣．

实际上,问题恰恰出在教学过程的过于“顺利”与“活跃”上．针对八年级的学生,尤其是在数学基础较好的班级,用折纸来引入等腰三角形的性质有明显的弊端．其背后的思考就是如此的折纸活动是否“稚化”了学生思维,导致课堂上缺少有含金量的生成．

由于学生对等腰三角形纸片进行折叠,都会采用同一种操作,并在纸片上留下一道折痕,这种唯一性限制了学生的想象,也弱化了学生观察图形、添加辅助线的能力．在不作提示下,学生的思维处于发散状态,可能会产生各种想法,并进行多元的数学表达．有意思的是,欧几里得在编写《几何原本》时将命题“等边对等角”排得比较靠前,以致证明时只有“边角边”可用,因此他采用的就是一种现在看起来不常规的思路．

认知教育心理学家奥苏贝尔指出:影响学习最重要的原因是学生已经知道了什么,应当根据学生原有的知识状况进行教学．可以说,教学内容与学生学情永远是实现折纸教学意蕴的起点．笔者认为,在本课教学中,不妨将折纸活动“悬置”,先给学生充分的时间进行自主探索．在经历了共同学习之后,对部分仍有困难的学生,用折纸活动辅助理解．实验探究、直观发现、推理论证都是研究图形的重要途径,折纸教学作为一种实验探究教学,其设计应充分考虑学生在认知需求方面的差异．

2 折纸教学的开发

文[2]在比较了中日两国教科书中折纸活动的设置后指出:中日两国数学教科书中设置折纸活动的目的不同,中国将折纸视为一种单纯的活动,主要让学生在折纸活动中体验数学学习,而日本则将折纸看作发现数学的一种手段,旨在通过折纸培养学生探索发现的精神,即前者是“在折纸中体验数学”,后者是“将折纸融入数学”．要做到将折纸融入数学,这无疑为今后折纸教学的开发指明了方向,笔者认为可以从以下几个方面进行尝试.

2.1 将折纸融入几何教学

数学折纸活动一般发生于几何教学中,首先需要分析折纸与几何学科的联系．折纸与尺规作图一样,都对现实世界的经验进行了抽象,但是这种抽象并未完全舍弃物理背景,其本质上仍然是建立在经验直觉之上．在日常教学中,教师应指导学生了解折纸与尺规作图的联系以及折纸的基本规则,帮助学生顺利地表达操作过程．

案例2折三角形的“心”．

在学习了三角形的重心、内心、垂心、外心等知识之后,学生可以通过折三角形纸片来确定这些“心”的位置,二者的联系见表1．

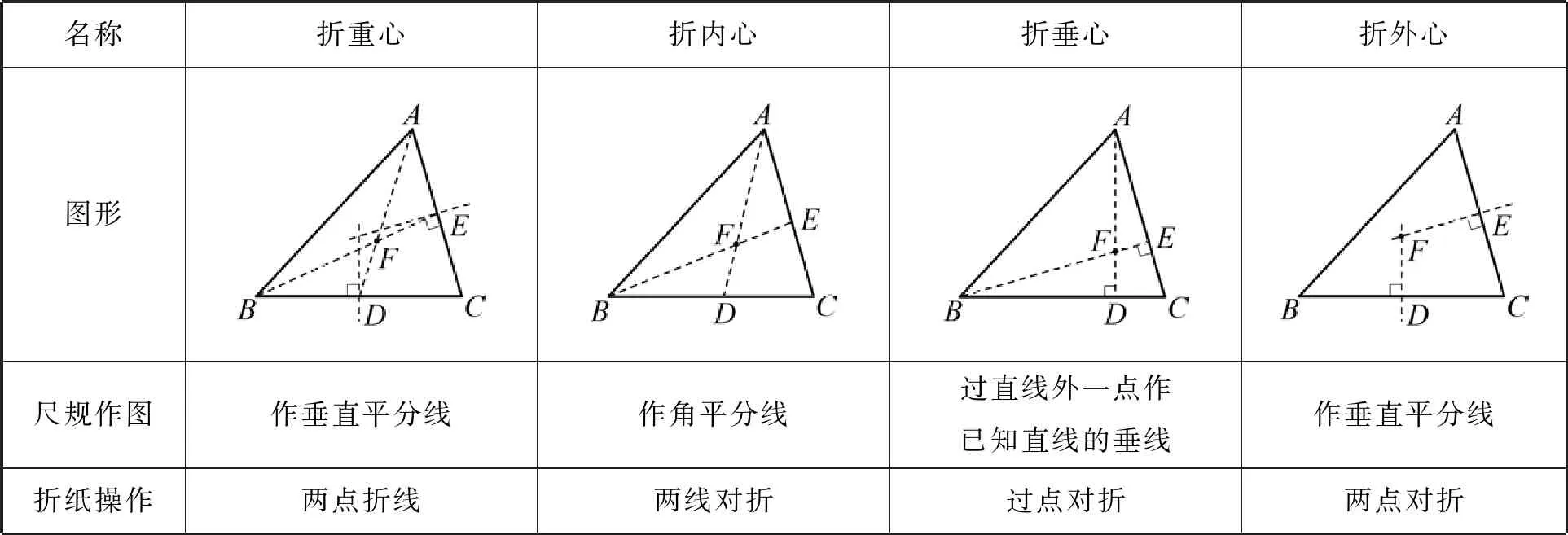
表1 折三角形的“心”与尺规作图的对照

在几何教学中借助折纸活动,有助于学生理解图形与图形的关系,发展空间观念和推理能力．

2.2 将折纸融入代数教学

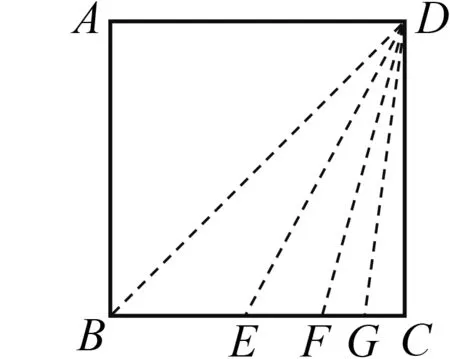
图1

目前而言,学生在折纸中的学习仍然比较单一,着眼点在于某一个几何知识的体验或者建构．与日本折纸教学相比,我们还缺少在代数教学方面的尝试．

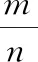
学生借助动作表征能更好地上升到对符号表征的理解,这正是具身认知的优势．另一方面,折纸的过程既可以复盘再现,也可以推进新的问题．学生回顾知识或者继续思考,这些都是将折纸融入数学的体现．

由于折纸运用了三维空间,因此其中所体现的数学原理也比尺规作图复杂．教师结合教学需要,可以设计出许多与折纸有关的代数问题．例如:

问题1如图2,点E,F分别是矩形纸片ABCD的边AD,BC上的点,将纸片沿着EF折叠,B′F与AD交于点G,试探究:怎样折能够使△EFG的面积最大?

(此为一次函数问题)

图2 图3

问题2如图3,将正方形纸片ABCD折叠,使折痕①与边AB平行,打开后再次折叠使点B和点E重合,出现折痕②,两条折痕交于点G．将上述操作重复进行若干次,可以观察到点G的不同位置形成一条曲线,试探究:这是一条怎样的曲线?

(此为二次函数问题)

2.3 将折纸融入作业设计

在素养目标的指引下,当今的数学作业设计正在发生改变．带有数学任务的折纸活动完全可以设计为学生作业,从而打破纸笔作业“一统天下”的局面,使得数学作业能够体现过程性、加强活动性、重视差异性,实现纸笔作业难以达到的效果．在九年级学习了“相似三角形”之后,笔者设计了一份这样的作业:

案例3折三等分点．

问题1利用尺规作图,作出线段AB的一个三等分点,你有哪些方法?

学生典型作法如图4、图5所示．

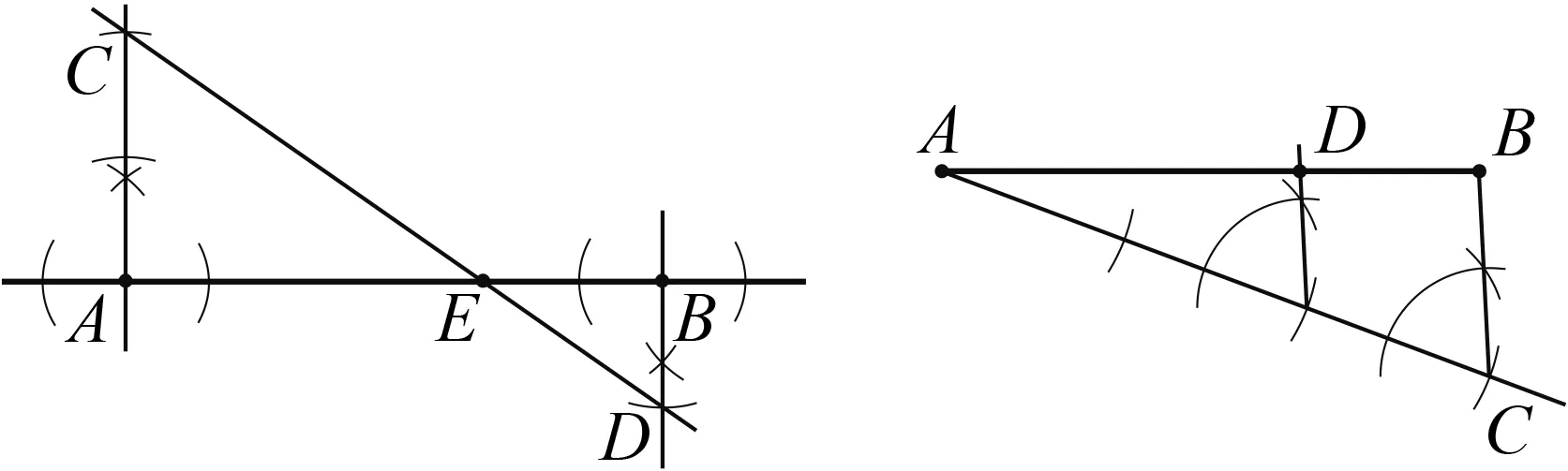
图4 图5

问题2取一张正方形纸片,你能通过折纸折出一边上的三等分点吗?如果你有方法(控制在6步之内),画出示意图,阐释其中的原理．最后从折法是否简捷、是否具有一般性等角度对自己的方案进行评价．

学生实际提交的方案有很多,有的图案绘制精美,有的理论叙述严谨．根据其中所用知识大体可分为三类:相似、勾股定理、三角函数．有一些折法与著名的日本芳贺和夫折纸三大定理一致,当然也有一些折法是错误的．鉴于此,备课组迅速跟进,制作了相应教学课件“‘纸’爱数学”,充分发挥了这节课的教学价值．以下是其中两个教学片断:

图6是学生提交的一种折法,并认为这种折法具有巧合性．教师点评:这种折法是有可能一次成功的,但是它是一个零概率事件．

图7是一种学生进行不下去的折法．教师点评:注意观察3乘3的正方形和4乘4的正方形,它们之间具有的位似关系．从失败到成功往往只有一步之遥(再折一次即可)!

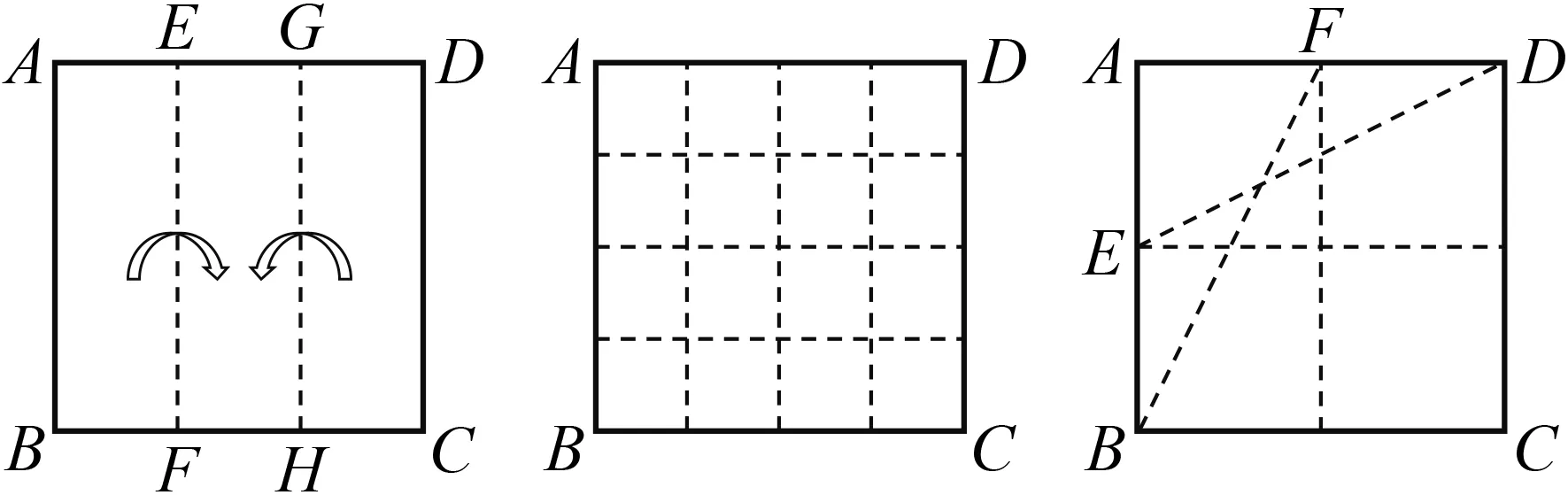
图6 图7 图8

图8是教师开发的一种“半成品”方案,请学生思考这种折法有没有利用价值(注意折痕BF,DE的交点相当于△ABD的重心)．让学生再次感受“多走一步就会成功”的体验．

3 折纸教学的实施建议

3.1 合理安排教学方式

林崇德指出:在少年期的思维中,抽象逻辑思维开始占优势,但在很大程度行还属于经验型,他们的逻辑思维需要感性经验的直接支持[3]．因此,在七年级开展折纸教学应当以直观为主,学生在折纸活动中对折垂线、平行线、三角形的三线等基本任务形成动作表征,增强空间观念．而在八年级与九年级应当开展一些具有较高思维含量的折纸教学．

《义务教育课程标准(2022年版)》对数学教学的课程目标、内容目标、实施建议、学业评价都提出了具体指导．教师应在课标的指导下灵活开展折纸教学,可以是一个课堂教学片段,也可以是一节完整的实验课,甚至是一个多课时、跨学科的项目式学习,也可以设计为课后作业．以“图形与几何”“数与代数”两大主题中筛选出的部分题材为例,来说明折纸教学的安排与建议(表2)．

3.2 善用数学实验教材

数学实验教材可以很好地弥补基础教材在指导学生活动方面的不足．以苏科版《数学实验教材(九年级全一册)》为例,该教材中设计了三个课时

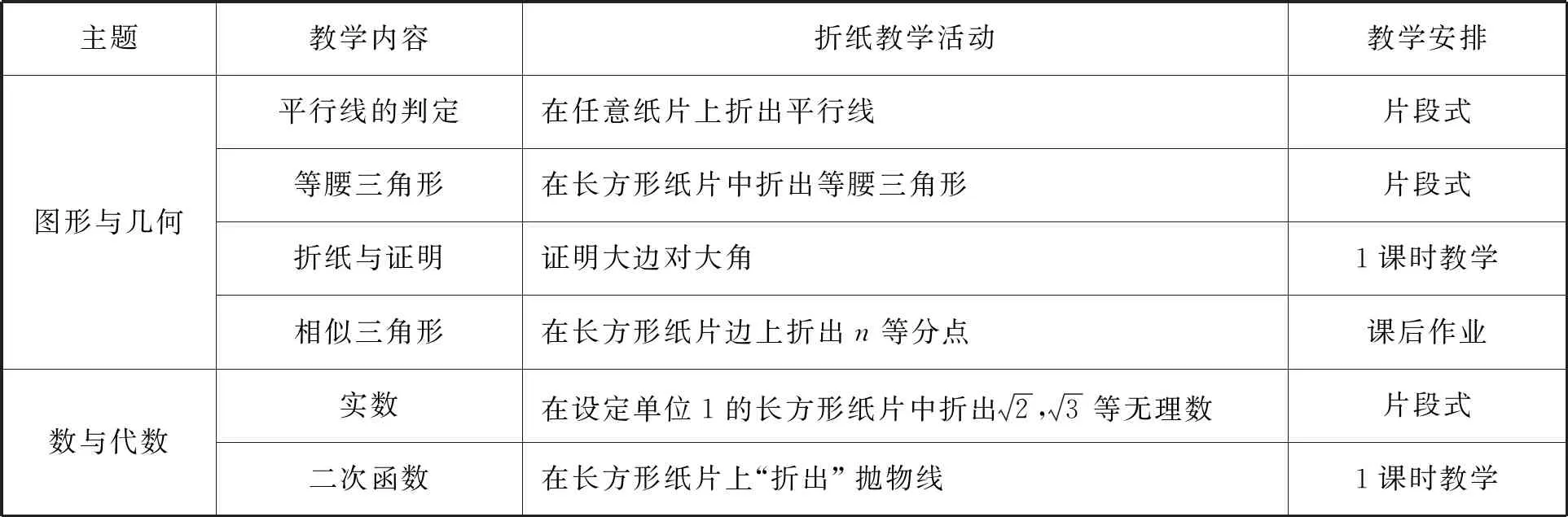
表2 部分折纸教学的教学方式建议

的折纸活动,分别是:利用圆形纸片折出正六边形;利用正方形纸片折出黄金矩形;利用正方形和等边三角形纸片折出一些特殊角,并计算这些角度的三角函数值[4]．这三个活动分布在圆、相似三角形、锐角三角函数等章节的学习中．

要发挥出教材中有关折纸教学应有的价值,关键在于如何整合以适应学生发展的需要．在利用圆形纸片折正六边形的教学中,可以设置如下:

初始环节可以是设计折圆心、折圆内接正方形等简单任务,以便逐渐过渡;拓展环节可以设计本质不变的进阶任务,以利于迁移,如:改变纸形为正方形,你还能折出正六边形吗?引导学生抓住构造正六边形的中心角60°这个解决问题的关键．

教师创造性地使用教材,方能促进折纸教学能与常规教学一样做到“源于教材,高于教材”．

3.3 着力于学生能力发展

不能发展学生数学能力的折纸教学应当坚决予以摒弃．喻平认为,数学关键能力的形成和发展依赖两类知识,分别是外显性知识和内隐性知识．外显性知识是外显的、静态的结果型知识;内隐性知识是指不以文本形式显性表述的,潜藏于显性知识深层的知识,包括数学知识的文化元素、数学知识的过程元素、数学知识的逻辑元素、数学知识的背景元素、学生错误认知资源、外显知识的推广与拓展等,品格与价值观的培养基本上依托于内隐性知识的作用[5]．如果局限于显性知识,把折纸教学仅仅作为单一知识的教学或者某一道题的教学,那就违背了折纸教学的初衷,不利于实现以数学折纸活动发展学生关键能力、提升学生品格和价值观的高层次目标．

事实上,在数学折纸活动中蕴含着丰富的隐性知识,例如折纸有关的数学文化:作为古希腊尺规作图三大难题之一的三等分角,利用折纸可以轻松实现,其中的道理是什么;折纸有关的德育:学生在折纸的过程中发展持续探索和永不言弃的精神;折纸中的美学:利用矩形纸片可以折出黄金矩形;折纸中的审辨性思维:学生在面对一种错误折法时,如何进行证否．这些都是提升教学厚度、促进学生开展深度学习的资源．

总而言之,尽管学界对于折纸在数学学习中的价值已经有充分的认识,但是在初中阶段关于折纸教学的内涵挖掘仍是一片蓝海．如何将折纸自然而然地融入到学生的数学学习活动中去,需要一线教师的广泛实践与研究．

折纸教学目标的立意不能局限于“一折一得”,而应围绕学生数学核心素养的发展需要进行整体思考,在培养“四基”、提升“四能”的基础上,进一步探索折纸教学对学生的数学价值观念、数学思维品格、数学学习态度和学会数学学习等方面的提升作用．