“一题一课”模式下对数学问题本质的探索与实践*
卢红卫
(江苏省张家港市外国语学校 215600)
“一题一课”的主要目的是通过典型例题的解题研究、变式训练和反思总结的示范启发,引领学生从不同的视角去思考问题,巩固和深化所学知识,训练学生的思维,让学生掌握解决数学问题的策略方法,形成一定的解题技能,培养学生运用数学知识与方法分析问题、解决问题的能力[1].
1 聚焦深度学习,精选试题
高中数学各种试题繁多,教师在课堂一讲到底的灌输型课堂教学模式已不适应新课改的要求,而深度学习强调学生主动参与、内化知识、迁移应用、举一反三、融会贯通.为了更好地实现深度学习的课堂教学,教师应当改善教学策略,精选试题,试题的选择应能强化数学知识的理解和数学思想方法的运用,达到解一题而会解一类题.以下是2023届苏州市高三上学期期中考试的压轴题第22题,笔者结合班级学生答题情况,用一节课的时间与学生一起进行了探究.
题目已知函数f(x)=ln(1+x)-xlna,其中实数a>0.
(1)若实数a∈N*,当x∈(0,+∞)时,f(x)<0恒成立,求实数a的最小值;
2 剖析典型错误,探寻本质
通过投影仪展示部分学生的解答过程,让学生去解读考试过程中的书写过程,去寻找错误的原因,提出改进的办法.
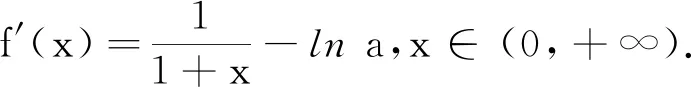
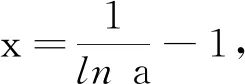
错误纠正
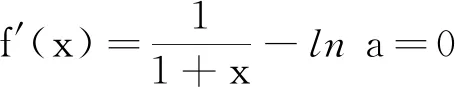
生:f′(x)=0有解只需要lna∈(0,1)即可,当lna<0时f′(x)>0,f′(x)=0无解;当lna>1时f′(x)<0,f′(x)=0无解.
师:因为已知当x∈(0,+∞)时f(x)<0恒成立,那么在lna的三种取值情况下,哪一种比较直观、容易研究呢?
生:当lna<0时f′(x)>0,此时f(x)在(0,+∞)上单调递增,f(x)>f(0)=0,这种情况舍去;当lna>1时f′(x)<0,f(x)在(0, +∞)上单调递减,f(x) 师:完全正确,那就只有lna>1,结合a∈N*,所以a=3.做好分类讨论的同时我们对每种分类情况也要注意图象特点,这样就避免了一些不必要的复杂计算. 错误纠正 师:虽然处理恒成立问题时分离变量的方法我们很熟悉,但利用洛必达法则求最值我们不熟悉,能否避开洛必达法则呢?由题目已知条件,当x∈(0,+∞)时,f(x)=ln(1+x)-xlna<0恒成立,得到ln(1+x) 生:先考虑y=ln(1+x)在x=0处的切线y=x恒在y=xlna的下方或重合.因为x∈(0,+∞)时ln(1+x) 师:那a 生:因为a∈N*,只需要看看a=1,a=2时是否成立即可. 师:完全正确!当然在大题的解答过程中ln(1+x) 点评教师不应回避学生的典型错误,而是要从学生的认知角度出发,对学生存在的疑惑进行针对性的解决.在典型错误剖析、纠正的同时,学生的解题能力也在同步提升,不同途径的思维展示使学生真正将新知识纳入到自己的认知系统中. 通过对以上典型错误的分析与纠正,学生思考后又提出以下问题: 问题1 因为a∈N*,先做a=1,a=2时是否符合,再做a≥3时,由a≥3时f′(x)<0,f(x)在(0,+∞)上单调递减,肯定符合,这样的讨论是不是更加简单了? 问题2 是否可以必要性探路?当x=1时ln 2-lna<0成立,则a>2,a∈N*,因为此题要求a的最小值,所以只要验证当a=3时是否符合就可以了. 全班学生对以上两个问题进行了思考与讨论,一致认为以上方案可行: 问题1注意到了a∈N*,分类讨论变得简单了; 问题2注意到了必要性探路,完全避开了分类讨论. 点评在课堂教学中,教师应鼓励学生提出自己的各种想法,然后大家一起探讨问题的不同解决方法的优劣,并进行方法归纳总结,形成数学迁移能力,有助于以后解决新的问题. 问题1 做证明题常用的方法有哪些呢?很多同学会想到分析法,先等价变形,但如何进行等价变形呢? 问题2 此题的第(1)问导数恒成立问题对第(2)问的证明是否有帮助呢? 学生在教师的提示性问题下进行思考尝试,最后给出了如下三个解题方案: 方案1分析法目标引领下进行取对数、换元、找中间量,转化为熟悉的不等式问题. 因为3m>em,而em>m+1(需补充证明),所以3m>m+1. 方案3从不等式左边出发,进行二项式展开,放大通项,朝着有利于求和的方向去化简,还是比较容易达成目标的. 点评对于较难的问题,教师可以做适当的启发引领.课堂教学中教师的“教”应与学生的“学”有机结合,教师的“教”并不是一讲到底,而是需要合理设置问题,引领学生积极参与,主动理解、消化和运用所学知识. 结合对以上问题的分析与讲解,教师设计了一道与此题方法类似的拓展引申问题让学生进行练习,以巩固解题的方法规律. 拓展引申 已知函数f(x)=ex+1-(lna)x-lna-1,实数a>0,若实数a∈N*,当x∈(-1,+∞)时,f(x)>0恒成立,求实数a的最大值. 要做好“一题一课”的教学,需要教师在平时的教学中善于发现问题,总结方法,提炼规律.“一题一课”因目标明确,思维深刻,能使学生在学习过程中进一步深化理解和巩固数学知识,提高“发现问题、提出问题、分析问题、解决问题、反思问题”的数学问题解决能力以及归纳、猜想、推理、证明的数学探究能力,促进良好的数学思维品质和关键能力的形成与发展,发展数学核心素养.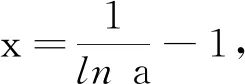
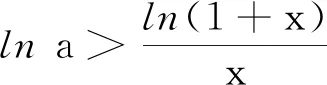
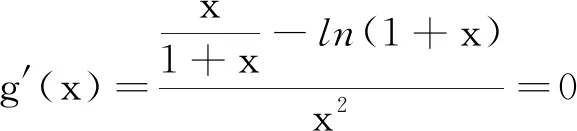

3 鼓励提出问题,自致其用
4 引领多维思考,提升思维
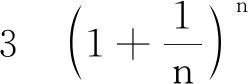
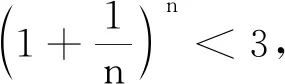
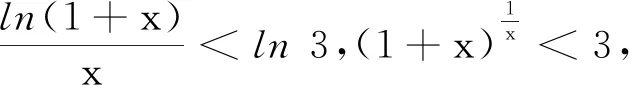
5 注重拓展引申,触类旁通

