基于灰色马尔科夫模型的北京市快递业务量预测

耿文叶 刘斯缇

(广州商学院管理学院 广东广州 511363)

自20世纪80年代快递产业进入我国后，其业务范围不断扩大。2020年1—12月，北京市快递服务企业业务量累计完成23.82亿件，同比增长4.16%；2021年1—9月，北京市快递服务企业业务量累计完成16.37亿件，同比下降5.82%。由此可见，北京市快递业务量和快递业务收入持续快速增长，但同时也增加了运输配送环节的燃油消耗，产生了大量快递包装废弃物，导致快递碳排放增多。因此，需要对快递业务量进行科学合理的预测，以最大限度地发挥快递业对经济增长的促进作用。

本文利用灰色模型和马尔科夫预测的优势，利用马尔科夫原理对灰色预测值进行修正，构建基于GM-Markov的快递业务预测模型，对北京市2021—2023年的快递服务企业业务量进行预测分析。

1 基于GM-Markov的预测模型

1.1 灰色GM(1，1)模型

灰色GM(1，1)模型研究对象是小样本、信息少的不确定信息，对数据及其分布的限制要求较少，该方法通过数据累加、灰色模型、数据累减等步骤对原始数据的序列进行处理，得到规律性较强的生成数列后建模，GM(1,1)模型的建立过程如下：

(1)由原始数据，给出原始序列：

(2)基于原始序列，生成一阶累加序列：

其中：

(3)对x(1)建立一阶线性微分方程：

式(2)中：a和b为未知参数，a为发展系数，体现了系统行为变量与其背景之间的动态关系，b为内生控制灰色，是灰色系统内涵外延的体现，方程解的形式为指数函数：

其中：

(4)解出时间相应函数为：

1.2 GM-Markov模型

本文利用北京市统计局统计的2011—2020年快递业务总量年数据，样本量少，符合灰色预测模型特点。因此本文在对北京市快递业务总量进行预测时，先用灰色 GM(1，1)预测模型对预测的快递业务量发展趋势进行大致判断，然后用马尔科夫原理中状态转移矩阵有效地反映数据的波动程度。

(1)由GM(1，1)模型的预测结果，计算原始值与灰色预测值的残差值，其中K=1，2，…，N：

(2)由残差的大小确定马尔科夫状态区间：

(3)计算状态转移概率矩阵：

其中，

mij为由Ei状态一步转移到Ej状态的次数，Mi为Ei状态一步转移出现的总次数。

(4)计算灰色马尔科夫预测值：

预测状态高时取正，预测状态低时取负。

1.3 基于GM-Markov模型的预测过程

GM-Markov预测模型的具体预测过程主要包括灰色GM(1，1)预测模型构建和利用马尔科夫原理对GM(1，1)模型修正两个阶段。

(1)灰色GM(1，1)预测模型构建。首先，进行数据选择，选取2011—2020年北京市快递业务总量年数据；其次，对数据进行数据级比检验，判断数据随时间变化的可行性，若数据不具有可行性，进行数据变换处理；再次，确定数据矩阵和系数矩阵B；最后，用GM(1，1)模型进行预测，得到预测结果。

(2)利用马尔科夫原理对GM(1，1)模型进行修正。先计算GM预测结果与真实值的残差及相对误差，然后依据残差进行预测状态划分，计算状态转移概率矩阵P，最后判断GM预测结果所处的状态，利用公式(14)对GM预测结果进行修正。

2 数据级比检验

在构建模型之前，本文对北京市2011—2020年快递总量数据做了平滑性检验，数据如表1所示，判断数据随时间变化的可行性，增加模型预测的准确性。

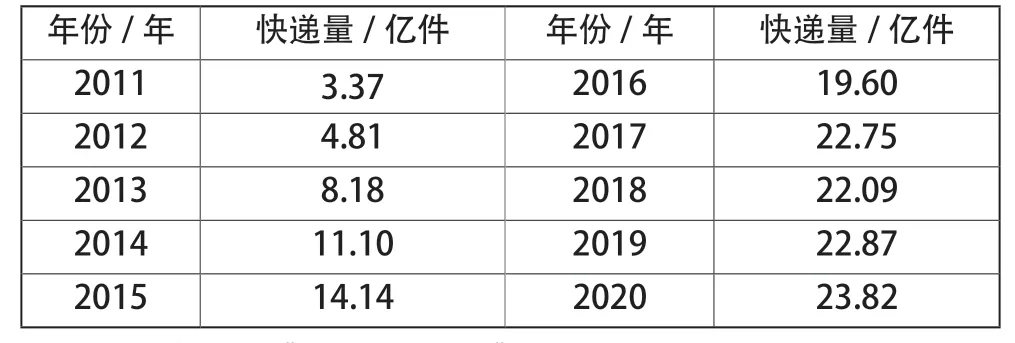
表1 北京市2011—2020年快递业务总量

对于数据序列：

定义级比：

3 构建灰色GM(1，1)预测模型

由表1可看出，北京市快递业务总量近年来总体呈上升趋势，符合灰色预测模型的特点，因此采用灰色预测模型进行预测计算。

建模运算过程如下：

(1)原始数据：

(2)经公式(1)一阶累加序列得：

(3)对一阶累加序列x(1)建立微分方程，通过公式(4)解出未知参数，其中，

(4)相应时间预测序列为：

(5)累减还原经公式(7)计算得到预测值为：

通过GM(1，1)模型对北京市2011—2019年快递业务总量进行拟合可以发现，GM(1，1)模型的拟合值与实际值误差较大，由此说明该模型的预测精度不高。

4 利用马尔科夫原理对GM(1，1)模型进行修正

4.1 划分预测状态

(1)计算原始值与灰色预测值的残差相对值及残差，经过计算得∈(-4.61,4.35)，∈(-958,0.191)，=22.36%。

(3)计算状态矩阵。根据各年份预测结果所在的状态区间，由公式Pij=P(Eij/Ei)=P(Ei→Ej)=mij/Mi可知如果初始状态Ei的初始向量为V0，经过k步转移后，状态向量为Vk=V0*Pk。在实际中，只需要考虑P中第i行，若max(Pij)=Pik，则可以认为下一时刻系统最有可能由Ei状态转向Ej状态确定状态Ei→Ej的一步转移概率，可以得到一步状态转移概率矩阵P。

4.2 预测结果对比

通过灰色马尔科夫预测模型可得2011—2020年的预测值(见表2)，同时该表将GM(1,1)模型与灰色马尔科夫模型的预测值与实际值相对误差进行比较。从实际值与预测值的平均相对误差来看，灰色马尔科夫模型的平均相对误差为0.100，而GM(1,1)模型的平均相对误差为0.224，由此充分证明了灰色马尔科夫预测模型的预测质量高于灰色模型。将GM模型与GM-Markov模型的预测结果进行对比分析(见图1)发现，灰色马尔科夫模型长期预测的效果优于短期预测，并且其预测结果的拟合效果明显优于灰色模型。

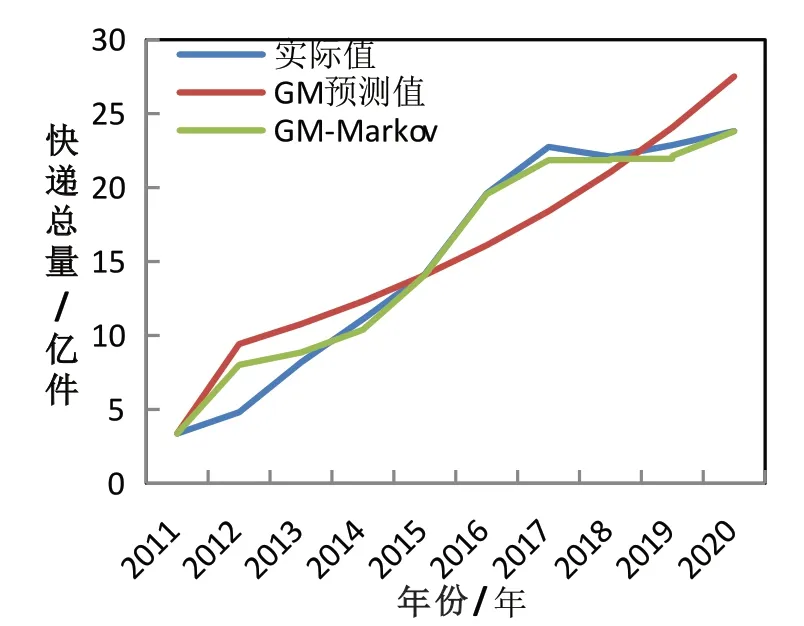
图1 模型对比分析

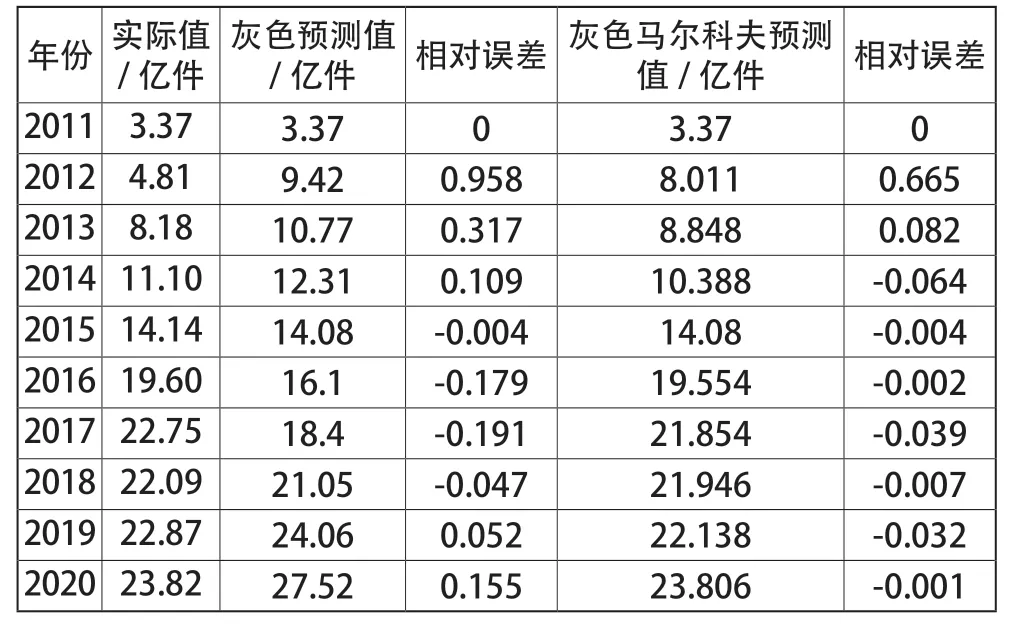
表2 GM模型与GM-Markov模型预测结果对比

由此可见，灰色马尔科夫模型的预测效果比GM(1,1)模型更为理想，因此本文选用灰色马尔科夫模型对2021—2023年北京市快递业务总量进行预测，预测结果如表3所示。

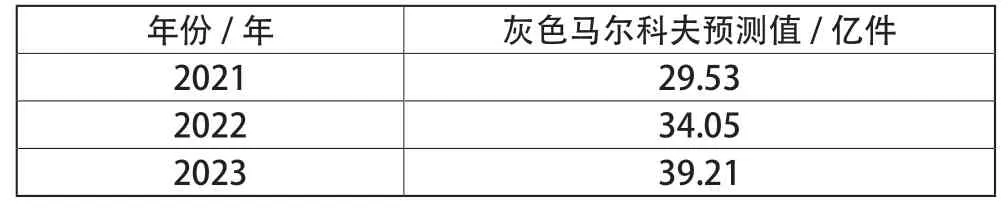
表3 北京市2021—2023年快递总量预测值

5 结语

首先，本文将灰色模型与马尔科夫状态转移矩阵相结合，构建了北京市快递业务总量预测的灰色马尔科夫(GMMarkov)模型。

其次，通过GM(1,1)模型与GM-Markov模型的预测值与实际值的平均相对误差进行比较，验证了本文所提出的GM-Markov的预测效果更理想，精度更高。

最后，运用GM-Markov模型预测了北京市2021—2023年的快递业务总量。

由预测结果可知，未来几年内北京市快递业务量将会不断增加。据此，政府可以及时调整对北京市快递行业制订的低碳经济发展规划，以最大限度地发挥快递业对经济增长的促进作用。