基于深度学习的期权价格预测研究

张贺鹏 周伟(通讯作者)

(兰州交通大学数理学院 甘肃兰州 730070)

1 绪论

1.1 研究背景及意义

在金融市场的形成过程中，金融衍生品所拥有的风险转移或套期保值功能，使其逐渐出现在人们的视野中。而期权以其特有的高杠杆特性，以及其具有非线性损益结构、尖峰厚尾等结构特征，更因其发挥了风险投资、价值发现、套期保值等功能，受到投资者们的推崇。

直至今天，期权市场仍在飞速发展，学者们对于期权理论的相关研究也愈加深入。在期权价值确定方面，对于期权定价相关研究，1973年，Fischer Black和Myron Scholes基于市场有效等一系列假设，提出了第一个完整的Black-Scholes期权定价模型[1]，但由于实际的期权交易市场无法满足其一系列理想化的假设条件，因此在实际应用中一般会产生较大误差。

随着大数据时代的到来，学者们着眼于研究以历史数据为驱动而构建的深度学习理论。在寻求误差最小化的过程中，机器学习及神经网络的出现，可以借助现实市场中的实际数据对神经网络模型进行训练与测试，最终达到规避理想化的模型假设及数据不兼容问题的目的。

1.2 研究思路及框架

本文以期权作为研究对象，基于B-S期权定价公式，结合深度学习相关理论构建出符合预期的期权价格预测模型。

首先，在对B-S期权定价模型进行充分研究后借助深度学习理论的优势，在文中结合B-S公式，应用深度学习理论中的神经网络方法构建期权价格预测模型，以期根据现存期权相关数据对未来的期权价格进行精度较高的预测与分析。

其次，对比分析利用BP神经网络及LSTM神经网络构建出的模型所预测出的期权价格，同时运用多种评价指标对预测值与真实值之间的误差进行分析对比，并评价模型拟合程度。

1.3 文献综述

1.3.1 期权定价模型

有关期权定价理论的研究最早在1900年被提出，Louis Bachelier以“投机交易理论”为基础，首次提出了用随机游动思想给出股票价格运行的随机模型，它被公认为现代金融学的里程碑[2]。

1973年，Fischer Black和Myron Scholes在对期权市场做出严格假设的情况下，提出了第一个完整的期权定价模型，即B-S期权定价模型，这篇文章的发表为后来学者研究期权定价理论提供了根本框架。同年，Merton在其基础上进行修改，使之更加接近现实情况，发展出了Black-Scholes-Merton模型[3-5]。

在具有期权性质的各种实物定价方面，龙海明(2007)等将B-S期权定价模型应用于消费贷款定价，指出对贷款抵押物处置灵活度较高的银行可以用期权定价法代替传统成本加成定价法来确定消费贷款利率，理论依据是抵押物价值的不确定性将给贷款带来风险，银行可以持有以抵押物为标的物的欧式看跌期权来对冲风险，进而基于这个枢纽将B-S期权定价模型应用于贷款价格的确定上[6]。冯芬玲等(2012)将二叉树定价法应用于铁路货运价格制定，使得传统固定协议定价所导致双方都不能从铁路货运现价波动中获利的弊端得到克服[7]。

1.3.2 基于深度学习的期权价格预测模型构建

Hutchinson等人首先将深度学习中的神经网络方法应用于期权价格预测，他们以标准普尔500指数期货期权为实证对象，建立神经网络模型，通过对比四种模型估计方法，经过反复训练后得出神经网络模型，其精度较B-S期权定价模型有所提高[8]。Anders等人比较了神经网络模型和B-S期权定价模型在DAX30期权定价过程中的表现，发现神经网络模型的定价准确度高于B-S期权定价模型[9]。国内的一些研究如2021年，Liu等人在基于自注意力机制(Self-Attention Mechanism)的神经网络中引入了特殊的期权定价形式，在如欧式和亚式期权等的情景下，比之前的方法更准确地捕获了期权时间价值的特征[10]。

2 相关理论基础介绍

2.1 B-S期权定价理论

B-S期权定价模型，主要用于为欧式期权定价。B-S对市场做出了以下假设：

(1)市场无摩擦，即不存在交易成本与税收；

(2)市场是完全的，可以无限制卖空，不存在无风险套利机会；

(3)标的资产的价格运动遵循几何布朗运动，即标的股票(以下均假设标的资产为股票)的收益率和波动率均为常数；

(4)标的资产收益为0，即在到期日内标的股票无现金收益；

(5)标的资产可以任何数量在任何连续时间交易；

(6)在期权的到期日内，无风险连续复利利率是一个常数，且任何期限内的借贷利率均相等。

基于以上假设，可以得出欧式看涨期权的表达式：

式(1)中：C表示欧式看涨期权的市场价格，S表示期权交割价格，N表示正态分布的累积概率函数，X表示期权的行权价格，r表示无风险利率，

根据欧式看涨期权与看跌期权之间的关系，即C+Xe-r(T-t)=P+S，可以得出欧式看跌期权的定价公式为：

2.2 深度学习相关理论

2.2.1 BP神经网络

BP神经网络算法可分为以下六个步骤：

(1)对网络中所有权值与阈值进行随机初始化，得到初始化连接权重；

(2)输入训练集，从前向后依次计算；

(3)基于各层输出结果，计算各输出层的误差；

(4)对于神经网络中的每一个隐含层单元k，计算其误差项；

(5)通过得到的各层的误差项，对权重进行调整训练；

(6)对神经网络训练设置训练终止条件。若神经网络训练结果达到训练终止条件，则停止训练，若未达到，则返回第二步，直至满足终止条件后结束训练。

2.2.2 长短期记忆神经网络

LSTM神经网络通过门机制，使其可以有选择性地记忆或遗忘长短距离的信息，以防止信息过载。

(1)遗忘门

遗忘门的输入由上一时刻隐藏状态和当前时刻的输入共同决定。

(2)输入门

输入门决定t-1时刻输入保留至t时刻单元状态的多少；t时刻记忆单元的单元状态更新值由t-1时刻隐含层的输出与t时刻的输入共同决定；当前单元状态由t-1时刻状态和t时刻输入单元的状态共同决定。

(3)输出门

输出代表单元状态保留至输出时的剩余量；t时刻的输出门状态和单元状态共同决定t时刻的输出。

3 预测模型构建

3.1 样本选取

3.1.1 样本产品描述

基于上证50ETF的良好特性，本文实证研究所选取的样本主体是上证50ETF认购期权。该期权的标的资产为上证50ETF，即由上证50指数的50只样本股票组成的上市交易基金。

3.1.2 样本数据范围

本文样本数据的时间跨度为2022年1月1日至2022年12月31日，剔除因节假日等市场休市情形导致的缺失数据后，共得到13771组数据，数据均来自wind数据库。其中，选取2022年1月1日至2022年9月30日，共11657组数据作为训练集；选取2022年10月10日至2022年12月31日，共2114组数据作为测试集。

3.2 变量确定

3.2.1 输入输出变量确定

在确定输入变量指标的过程中，通过对B-S期权定价模型的理论研究，本文选取公式中的5个已知变量，包括期权从当前距离到期日剩余时间T、标的资产的市场价格S、期权的行权价格X、无风险利率r、标的资产价格的历史波动率σ(本文在数据中用HV表示，以示区分)。此外，本文还选择了影响期权市场价格的开盘价open、结算价SP、成交量deal、持仓量host这四个变量，共计9个指标作为输入变量，输出变量为当前收盘价格P。

3.2.2 数据预处理

(1)期权从当前距离到期日剩余时间T

将剩余时间T以年为单位进行转化。本文选取交易市场的实际天数，即交易日天数作为基数对距到期日剩余时间T进行转化，公式为

(2)数据归一化

本文采取离差标准化的方法对原始数据进行归一化，而且未对无风险利率r及历史波动率HV进行归一化。

3.3 期权价格预测模型构建

本文使用python构建神经网络模型，使用版本为3.8.0。

3.3.1 基于BP神经网络的期权价格预测模型构建

(1)网络结构设计及参数选择

本文构建三层BP神经网络，并选取tansig和purlin作为激活函数，选取traingdm函数作为训练函数，选取均方误差(MSE)作为损失函数。

本文在训练时，根据经验法则，首先设置最大允许误差为0.01；其次，利用训练样本对迭代次数进行训练并调整；最后，将迭代次数确定为100，学习率设为0.01。

(2)预测结果分析

采用BP神经网络所预测的期权价格如图1所示：

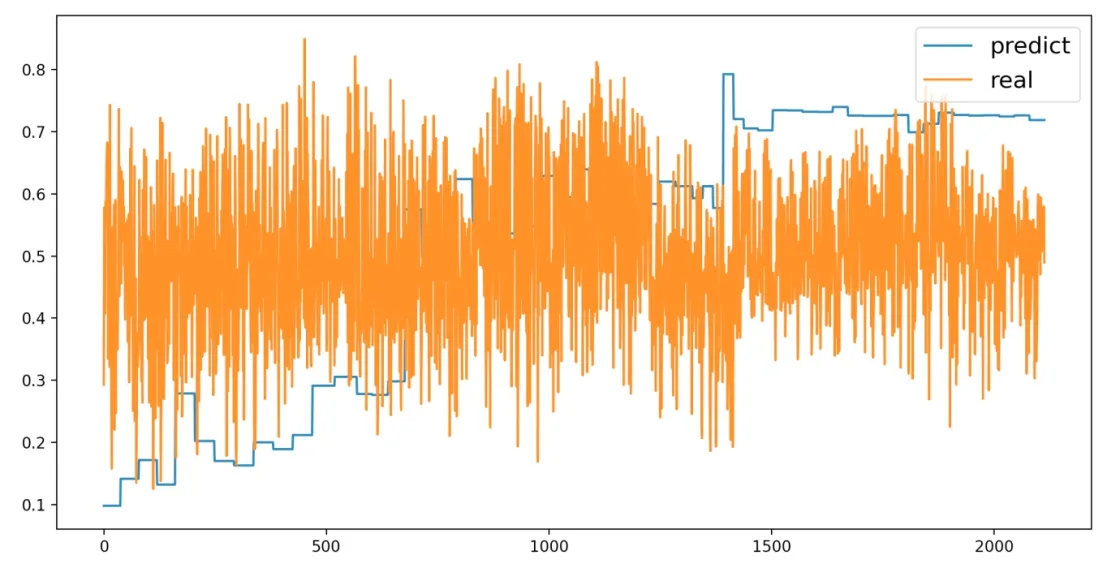
图1 BP神经网络模型期权价格预测结果

部分预测数据如表1所示：

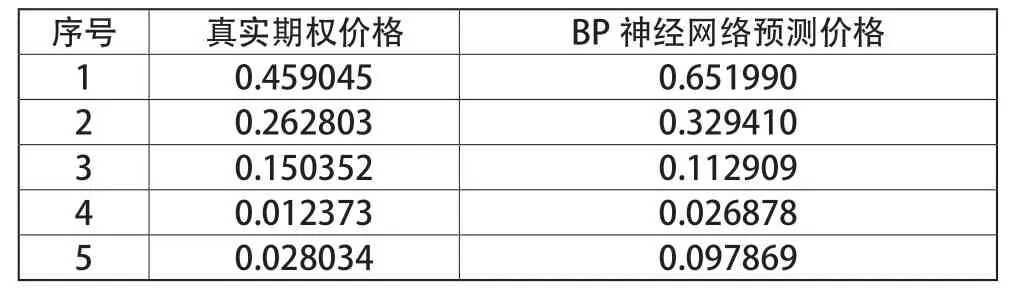
表1 部分预测数据(归一化后)

3.3.2 基于LSTM神经网络的期权价格预测模型构建

具体结构设计及参数选择如下：

(1)结构设计及参数选择

本文在模型划分数据集时，选择通过日期对其进行划分。其中训练集日期划分为2022年1月1日至2022年9月30日，共计11657组数据；测试集日期划分为2022年10月10日至2022年12月31日，共计2114组数据。

本文选择sigmoid函数作为三个门的激活函数，使用tanh作为隐含状态和输出状态的激活函数。

在LSTM模型层级结构设定方面，本文将LSTM层数设置为单层。选取均方误差(MSE)作为损失函数，优化器设置为RMSProp优化器。同时将fit函数中的epoch项定为30，batch_size项定为512。

(2)预测结果分析

采用LSTM神经网络所预测的期权价格如图2所示：

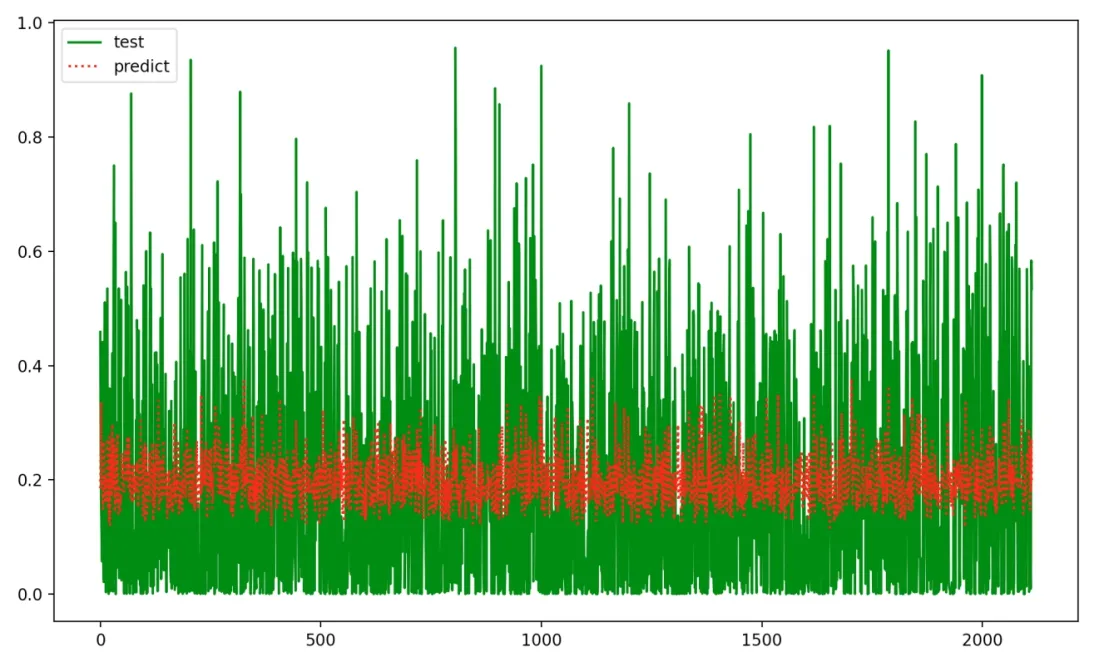
图2 LSTM模型期权价格预测结果

部分预测数据如表2所示：

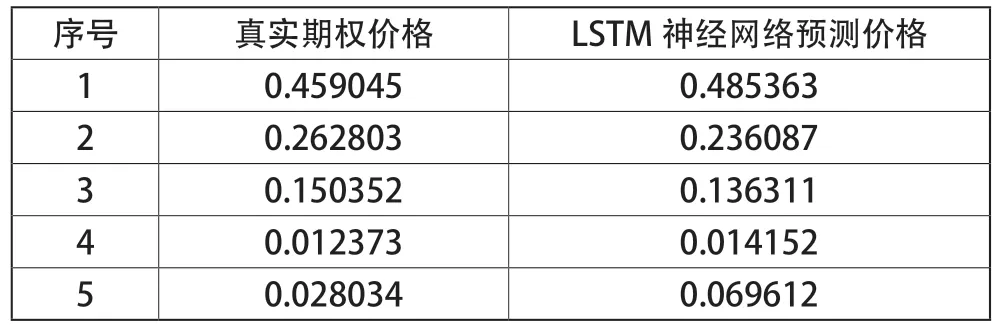
表2 部分预测数据(归一化后)

3.4 实证结果分析与对比

在上述期权价格预测模型的构建及预测过程中，本文通过计算各个模型的误差及拟合情况对各个模型的预测结果进行对比分析。这里选取三个评价指标作为模型评价指标，分别为均方误差、平均绝对误差及决定系数，综合使用多因素对模型优劣性进行评价，可以得出更为客观的结论。

(1)均方误差(MSE，Mean Squared Error)

MSE是指模型预测值与真实值之间差额的期望值。其表达式如下：

(2)平均绝对误差(MAE，Mean Absolute Error)

MAE是指模型预测值与真实值之间距离绝对值的平均值。其表达式如下：

(3)R2(决定系数)

R2是指回归平方和占总平方和的比例。R2越接近1，表明回归平方和占总平方和的比例越大，模型真实值与预测值越接近，神经网络模型的拟合程度就越好。其表达式如下：

使用MSE、MAE、R2三类误差评价指标对两个模型结果进行对比分析，如表3所示：

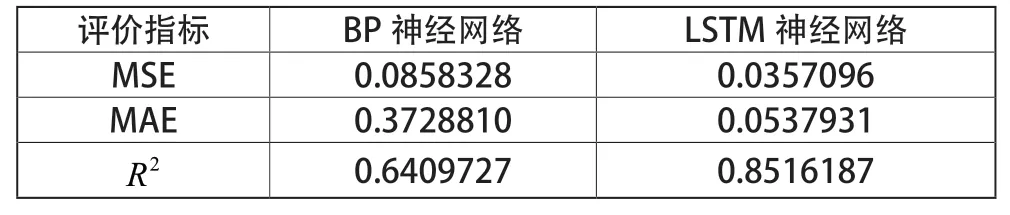
表3 神经网络模型预测结果对比

由表3可知，LSTM模型预测的精确度高于BP神经网络模型。

结合前述分析我们可以得出以下结论：相较于BP神经网络模型，LSTM神经网络模型具有更高水平的非线性组合运算能力，对于上证50ETF期权这一实证对象，显示出更好的拟合高维性金融数据的能力，其模型预测结果的精度较高。

4 结语

4.1 本文研究工作总结

本文分别利用BP神经网络和LSTM神经网络理论，选取上证50ETF指数的期权作为研究样本，建立期权价格预测模型，得出以下结论：

作为基于数据驱动的期权价格预测模型，LSTM神经网络预测的期权价格的精度高于BP神经网络。在三种模型评价指标下，LSTM神经网络在价格预测误差方面明显优于BP神经网络。LSTM神经网络具有独特的结构和较高的非线性计算能力，这使得它在有大量数据时能够更准确地预测期权价格。

4.2 不足之处与研究展望

本文对基于深度学习的期权价格预测进行探索，并取得了一些成果。但仍有一些地方存在不足之处，今后需要进一步改进：

(1)除本文选取的9个输入变量外，依旧存在诸多其他可能影响期权价格的因素，在后续的研究中可以进一步探索，从而使得期权价格预测模型的普遍性有所提升。

(2)文中选取的9个指标中，各个指标之间的相关性并未解决，这种相关性对于期权价格预测模型的影响也未可知。

(3)本文基于Black-Scholes期权所确定的输入变量之一选取了历史波动率，在相关文献中显示，若选择隐含波动率代替历史波动率，作为输入变量对期权价格预测模型进行训练，模型误差可能会减小。