随机行走人群-大跨楼盖耦合振动及MTMD减振分析

操礼林 王念康 李爱群

(1江苏大学土木工程与力学学院, 镇江 212013)

(2东南大学土木工程学院, 南京 211189)

(3北京建筑大学北京未来城市设计高精尖创新中心, 北京 100044)

随着结构逐渐向大跨、轻质与低频的方向发展,人群行走导致结构产生过度振动的问题不容忽视.评估结构振动是否满足舒适度要求时主要以加速度响应为指标,如需准确计算人群行走下的结构加速度响应,则应建立合理的行人荷载模型[1].行人在正常行走过程中每步的步频、步速与步长都具有随机性的特点,且不同时刻行人荷载力大小不断变化,故随机人群荷载模型比较符合实际情况[2].研究行人在结构上行走时需要考虑人-结构相互作用,若仅简单地将行人荷载简化为移动力,则忽略了相互作用力,会导致预测的结构动力响应与真实的人致振动响应相差较大[3].

当结构的振动加速度响应超过舒适度要求时,需要对结构进行减振处理.目前,学者们主要采用安装减振器的方法来降低结构的振动幅度,其中减振器包括单个调谐质量阻尼器 (TMD)或多重调谐质量阻尼器 (MTMD).惠晓丽等[4]采用单个TMD对单人行走及人群同步行走下的大跨连廊进行减振,发现单个TMD系统能够有效控制大跨连廊的人致过度振动.沈文爱等[5]以人行悬索桥为对象,设计MTMD系统参数,对人致结构振动进行控制,达到了理想的减振效果.由此表明,单个TMD与MTMD均具有良好的减振性能,MTMD在减振鲁棒性方面优于单个TMD[6-7].

目前,人致振动问题的研究已趋于成熟,而对于随机行走人群与大跨楼盖的耦合振动及考虑人-结构相互作用的MTMD参数优化设计研究还有待开展.本文基于随机人群行走荷载模型,推导了人群-大跨楼盖-TMD耦合动力方程,开展了随机人群行走下大跨楼盖动力特性参数及加速度响应的不确定性研究,建立了基于人-结构相互作用的大跨楼盖MTMD减振优化设计方法,并通过数值计算对比了单个TMD与优化MTMD的减振效果.

1 人群-大跨楼盖-TMD耦合方程

1.1 随机人群行走荷载模型

针对人行过程中步行参数随机性的特点,将行人行走过程等效为有限段步长的叠加.参考文献[8],建立行人步频与步速的关系式为

(1)

(2)

(3)

根据文献[9]中提出的与步速相关的单人行走荷载模型,可得行人i第k步的步行力荷载为

(4)

(5)

根据叠加原理,可将随机人群行走荷载表示为

(6)

式中,Si为行人i走完全程的步数;r为行走总人数.

1.2 动力方程

当人群在大跨楼盖上行走时,结构会出现过度振动,从而影响行人正常行走,因此需要对结构进行振动控制.图1为附加TMD减振系统的大跨楼盖示意图.图中,kTMD、cTMD分别为TMD减振系统的刚度和阻尼;a、b分别为大跨楼盖长度和宽度.

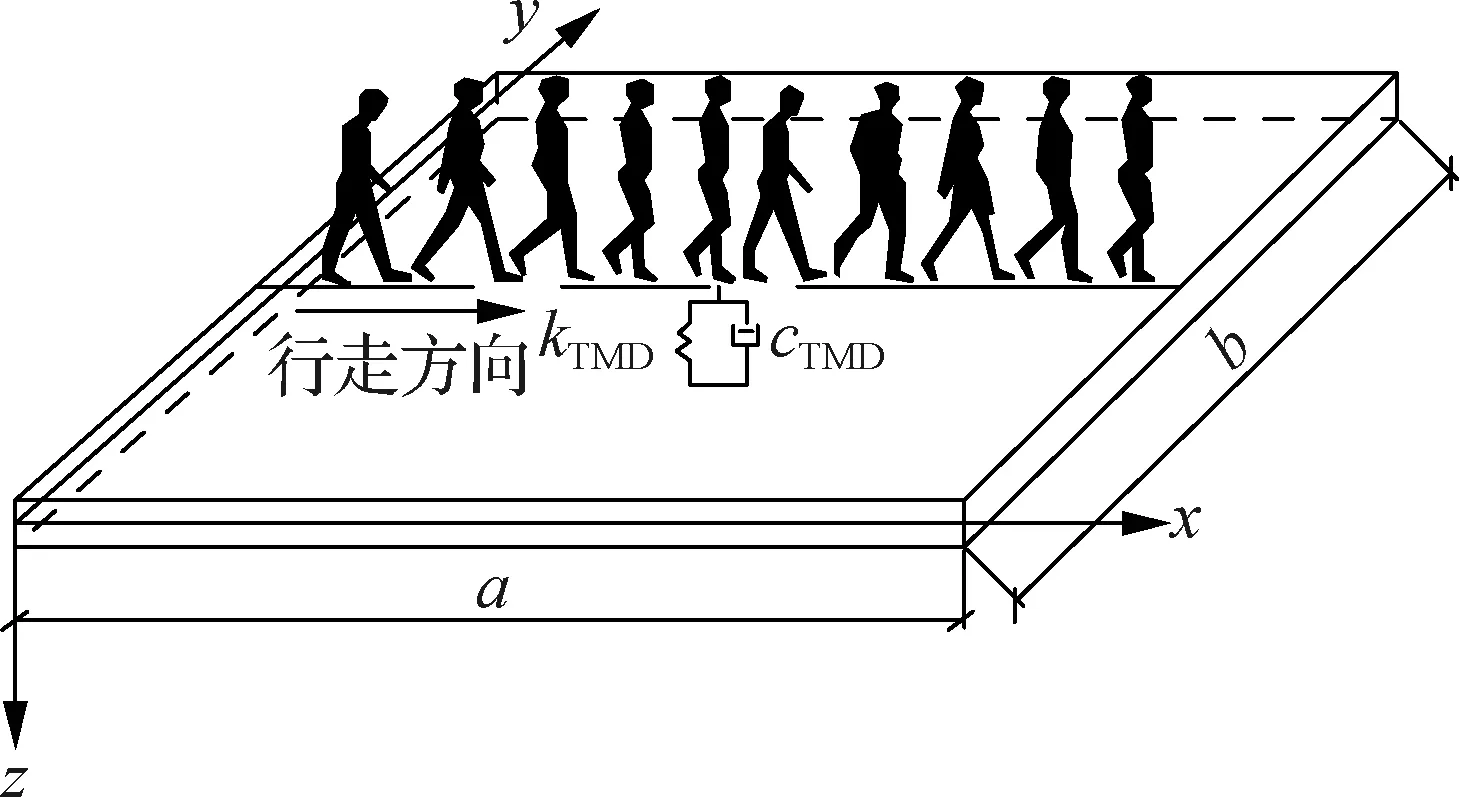
图1 附加TMD减振系统的大跨楼盖示意图

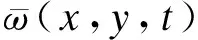
(7)

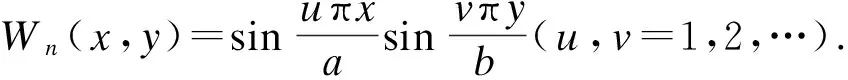
行人i的位移函数为zp,i(xi,yi,t),行人与楼盖一直保持接触,且板上的外部激励全部由行人行走引起.大跨楼盖的弯曲振动方程为

(8)

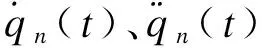
将广义质量归一化,模态函数正则化可得

(9)

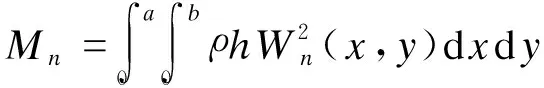
式(8)可转化为

(10)

式中,f(x,y,t)为大跨楼盖所受外荷载.

分析人群行走对大跨楼盖的影响,需要考虑人-结构相互作用,故本文采用人体质量-刚度-阻尼(MSD)模型,同时将TMD减振系统简化为质量-刚度-阻尼模型.假设大跨楼盖上包含若干个TMD减振系统,则减振系统j的位移函数为zd,j(xd,j,yd,j,t).当行人行走在包含附加TMD减振系统的大跨楼盖上时,人体与减振系统的动力平衡方程分别为

式中,mp,i、cp,i、kp,i分别为行人i的人体模态质量、阻尼和刚度;md,j、cd,j与kd,j分别为TMD减振系统j的质量、阻尼和刚度.

采用振型分解法,式(11)和(12)可分别转化为

(13)

(14)

由于大跨楼盖上附加了TMD减振系统,故楼盖所受的激振力由行人激振力和TMD减振系统引起的激振力2个部分组成,即

f(x,y,t)=fp(t)+fd(t)

(15)

(16)

(17)

式中,Fp,i(t)为行人i的行走激振力;Fd,j(t)为TMD减振系统j阻尼器激振力;s为TMD总个数.

(18)

联立式(13)、(14)、(18),可得人群-大跨楼盖-TMD耦合动力学方程为

(19)

式中

(20)

(21)

(22)

(23)

(24)

C11=diag(2ζlωl)l=1,2,3,…,N

(25)

(26)

(27)

(28)

(29)

(30)

q={q1,q2,…,qN,qp,1,qp,2,…,qp,r,qd,1,qd,2,…,qd,s}

(31)

(32)

针对上述非比例阻尼时变微分方程,利用状态空间法求解时变系统的模态特性,并采用变步长四阶五级龙格库塔法求解其动力响应.

2 随机人群行走下大跨楼盖振动响应分析

2.1 算例参数

对于某大跨钢-混凝土楼盖[11],a=9.144 m,b=9.144 m,h=0.222 m,ρ=2 322.9 kg/m3,泊松比为0.2,结构基频为4.98 Hz,前3阶阻尼比ζ取为1%,将此楼盖等效为四边简支的正交各向异性板.

人群行走路径如图2所示,共5条路径,行走路径长度均为楼盖宽度a.行走人数为r,每条路径各分配r/5人.行人初始进入结构的时间间隔为1 s,各路径行人同时出发,并依次排队行走,直至最后一人走完全程.由文献[12]可知,不同密度人群的步频服从正态分布.表1为不同行走人数对应的步频均值及标准差.

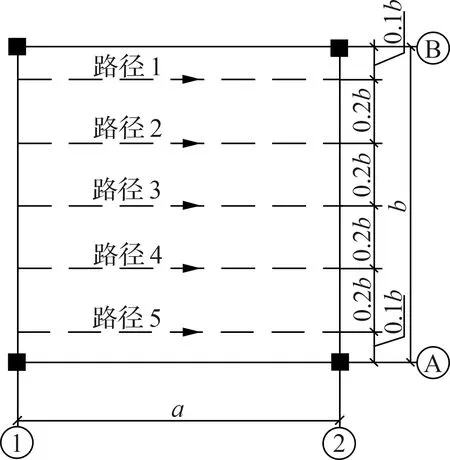
图2 人群行走路径

表1 不同行走人数下步频均值及标准差

人体质量服从对数正态分布N(73.85,15.682)kg[13].根据文献[14]中行人动力学参数与步频的关系式,确定行人MSD模型的模态质量mp,i、刚度kp,i、阻尼cp,i分别为

(33)

式中,Mp,i为行人i的实际质量;fp,i为行人i的步频.

2.2 结构动力特性参数分析

为研究随机人群行走下大跨楼盖动力特性参数的变化规律,对不同模态质量的大跨楼盖在随机人群行走下的动力特性参数峰值进行100次计算.其中,简支板模态质量为物理质量的1/4[15].假定结构基频与阻尼比恒定,模态质量分别取8 780、9 780、10 780、11 780、12 780 kg.

受行走参数随机性影响,每次计算结果均存在差异.因此,为研究随机行走人群对楼盖动力特性参数的影响,分别取100次计算的一阶瞬时阻尼比峰值的统计均值ζ1,in与一阶瞬时频率峰值的统计均值f1,in进行分析,结果见图3.图中,Dn为行走人数.

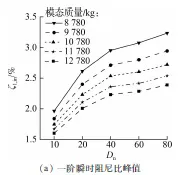
(a) 一阶瞬时阻尼比峰值

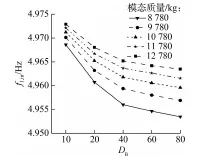
(b) 一阶瞬时频率峰值

由图3(a)可知,与大跨楼盖初始阻尼比1%相比,随机人群行走下的结构阻尼比变化较为明显.随着行走人数的增多,大跨楼盖一阶瞬时阻尼比逐渐升高.对于模态质量为12 780 kg的大跨楼盖,行走人数为10时,大跨楼盖瞬时阻尼比峰值均值达到1.60%,较空载时增大60%,说明随机人群与结构耦合作用明显.对于模态质量为11 780 kg的大跨楼盖,当行走人数为10时,大跨楼盖瞬时阻尼比峰值均值达到1.67%.大跨楼盖模态质量为10 780、9 780、8 780 kg时,10人随机行走下的结构瞬时阻尼比峰值均值分别上升至1.75%、1.84%、1.96%.由此可见,随着模态质量的减小,相同行走人数下大跨楼盖一阶瞬时阻尼比会逐渐升高.

由图3(b)可知,随着行走人数的增多,大跨楼盖一阶瞬时频率逐渐降低.对于模态质量为8 780 kg的大跨楼盖,当行走人数为80时,大跨楼盖瞬时频率峰值均值下降至4.953 5 Hz,人群-结构耦合作用明显.同时,对比分析模态质量为9 780～12 780 kg的楼盖瞬时频率峰值均值可知,随着结构模态质量的减小,相同行走人数下大跨楼盖一阶瞬时频率逐渐降低,且降幅逐渐增大.

2.3 结构加速度响应分析

为进一步研究大跨楼盖在随机人群行走下加速度响应的变化规律,取楼盖中心位置的竖向加速度进行分析,对不同模态质量的大跨楼盖在随机人群行走下的加速度响应峰值进行100次计算,结果见图4.图中,a1,in与a1s,in分别为瞬时加速度响应峰值的统计均值与1 s均方根加速度响应峰值的统计均值.

(a) 瞬时加速度响应峰值

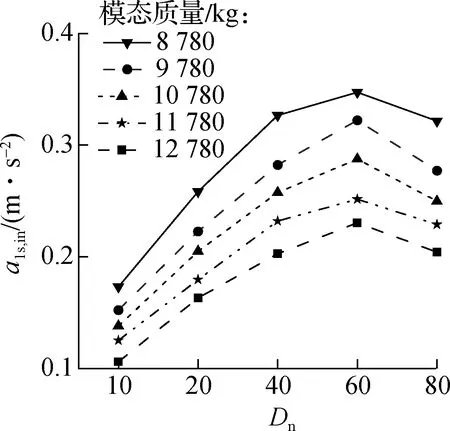
(b) 1 s均方根加速度响应峰值

由图4可知,当大跨楼盖模态质量为8 780 kg,行走人数从10递增到60时,大跨楼盖的加速度响应逐渐增加.行走人数为60时,楼盖加速度响应峰值均值达到最大值,其中瞬时加速度响应峰值均值为0.669 m/s2,均方根加速度响应峰值均值为0.347 m/s2.但随着行走人数的持续增加,大跨楼盖的加速度响应反而降低;这是因为随着人流密度的增大,高密度人群之间出现拥挤现象,个体步频与步速有所下降,从而导致结构振动响应降低.对比分析模态质量为9 780～12 780 kg的楼盖加速度响应峰值均值可以发现,随着结构模态质量的减小,相同行走人数下大跨楼盖的加速度响应逐渐增大.

3 大跨楼盖MTMD减振优化设计

3.1 MTMD减振优化方法

针对人群行走下大跨楼盖过度振动的问题进行减振设计.由于单个TMD具有调频范围窄、控制效果不稳定等缺陷,因此采用减振鲁棒性更强的MTMD减振系统.为了提高计算效率,本文的MTMD系统只设置了3个子TMD(见图5).3个子TMD以0.5 m的间隔沿x方向布置,其中TMD2安装在楼盖中心位置.

图5 大跨楼盖MTMD安装位置示意图

假设MTMD系统的平均频率与结构基频相同.第j个子TMD的频率为[16]

(34)

式中,ft为MTMD系统的平均频率;s1为子TMD个数;β为MTMD系统的频率间隔.

第j个子TMD的刚度与阻尼分别为

kd,j=(2πfd,j)2md,j

(35)

cd,j=2×(2πfd,j)md,jζopt,j

(36)

式中,md,j、ζopt,j分别为第j个子TMD的质量和阻尼比.

将楼盖基频不小于4 Hz、竖向峰值加速度不大于0.15 m/s2作为判断本文楼盖是否满足振动舒适度要求的标准[17].本文楼盖基频4.98 Hz已满足限值要求,为降低结构的加速度响应,使其满足舒适度要求,基于人群-大跨楼盖-TMD耦合动力方程,设计考虑人-结构相互作用的MTMD减振优化方法,主要包括以下2个方面:

1) 控制MTMD系统的经济性,设置系统总质量比μ=0.01,且使每个子TMD的质量和阻尼比均相等.

2) 控制频率间隔和子TMD阻尼比在限值范围内,采用遗传算法中的单目标优化算法,得到结构响应达到舒适度要求时每个子TMD的最优刚度和最优阻尼.

设计公式如下:

(37)

式中,Md为大跨楼盖质量;βmin和βmax分别为频率间隔的下限值和上限值,此处分别取为0.01和0.5;ζopt为TMD阻尼比;ζopt,min和ζopt,max分别为子TMD阻尼比的下限值和上限值,此处分别取为0.02和0.2.

3.2 人群行走下的结构减振分析

采用本文提出的MTMD减振设计方法,对人群行走下的大跨楼盖进行减振.选取40、60、80人行走下的工况进行减振分析,得到人群同步行走和随机行走下结构中心减振前后的加速度响应曲线(见图6).人群同步行走步频为1.66 Hz,即大跨楼盖基频4.98 Hz的1/3倍频.图中同时给出了采用单个TMD减振后的结果.单个TMD的参数根据文献[18]中的最优取值方法确定,即

(38)

fd=fopt+f

(39)

(40)

式中,fopt为最优TMD参数设计频率比;μs为TMD与结构质量比;fd为TMD系统的基频;f为大跨楼盖基频;ζopts为最优TMD参数设计阻尼比.

由图6可知,采用优化MTMD对大跨楼盖进行减振的效果显著.表2给出了各工况下结构中心减振前后的峰值加速度及提升率.由表可知,各工况下采用MTMD设计方法减振后的结果均达到楼盖舒适度要求,且与单个TMD相比,优化MTMD的减振效果提升明显,最大提升率为46.36%.究其原因在于,大跨楼盖结构具有多组竖向振型,单个TMD仅能控制其中某一振型,而优化MTMD系统则能针对结构的数组振型进行控制.

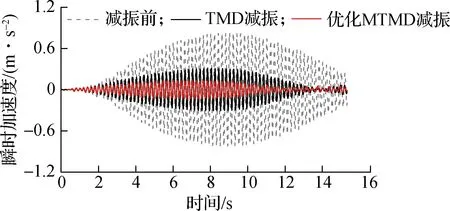
(a) 40人同步

(b) 60人同步

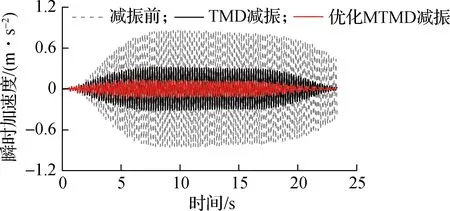
(c) 80人同步

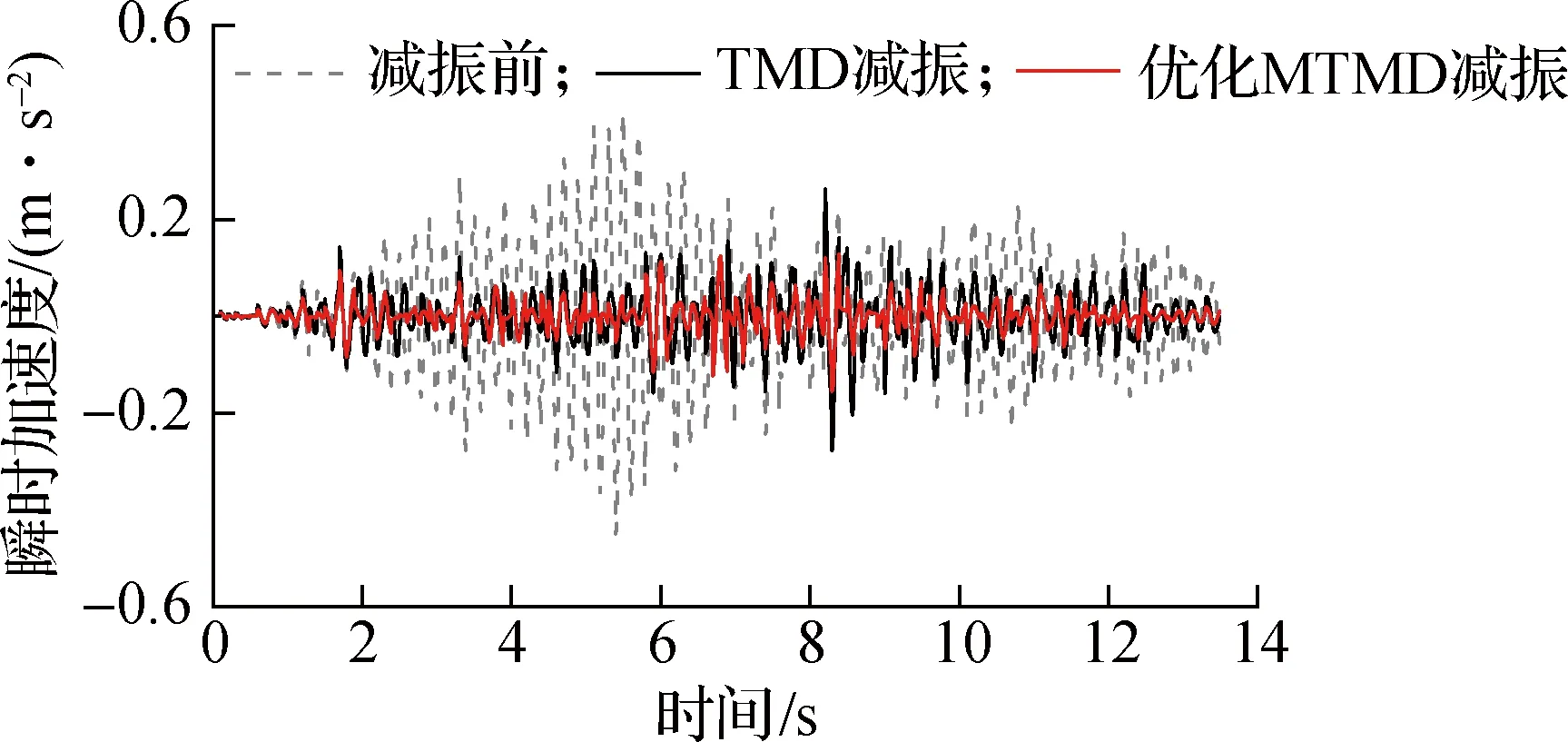
(d) 40人随机

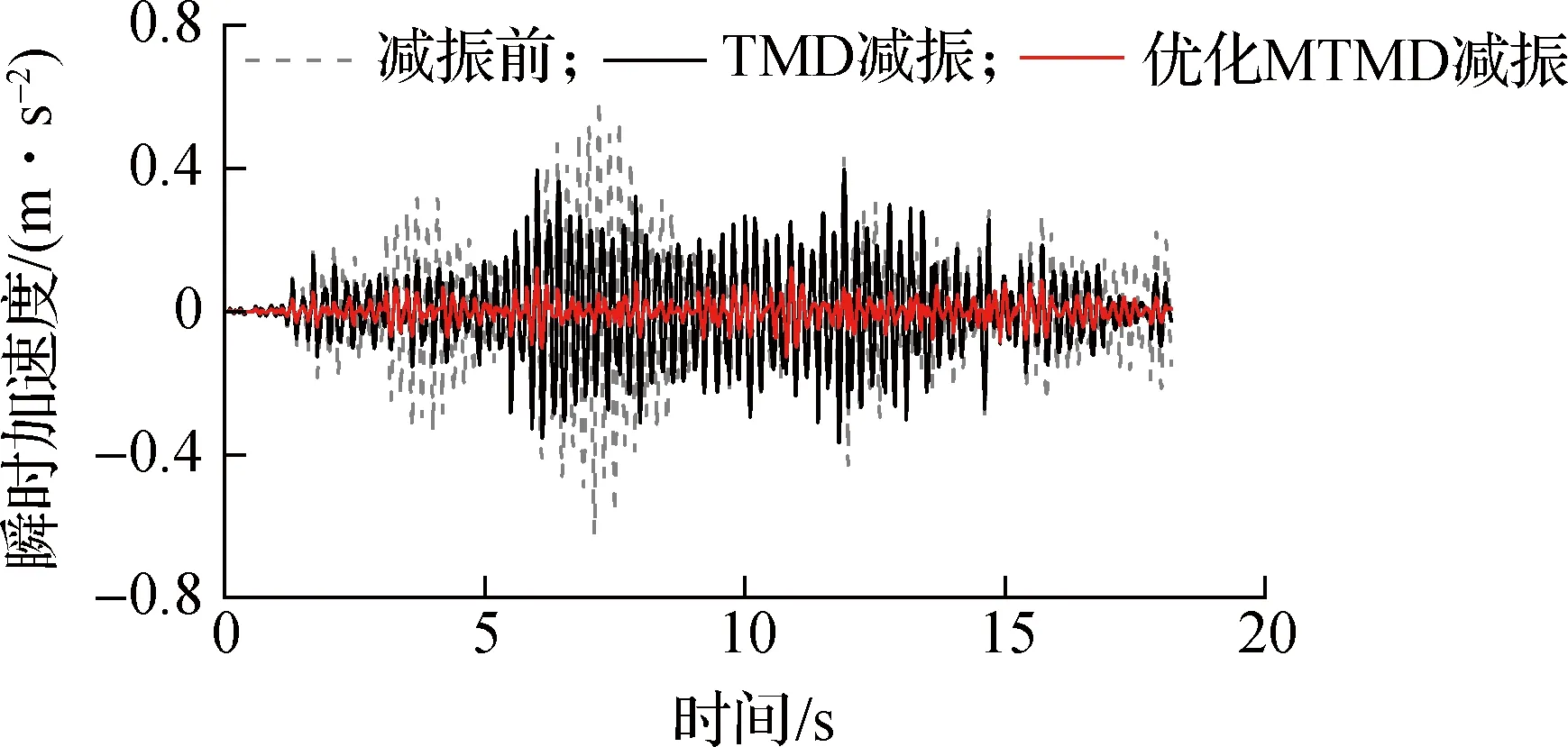
(e) 60人随机

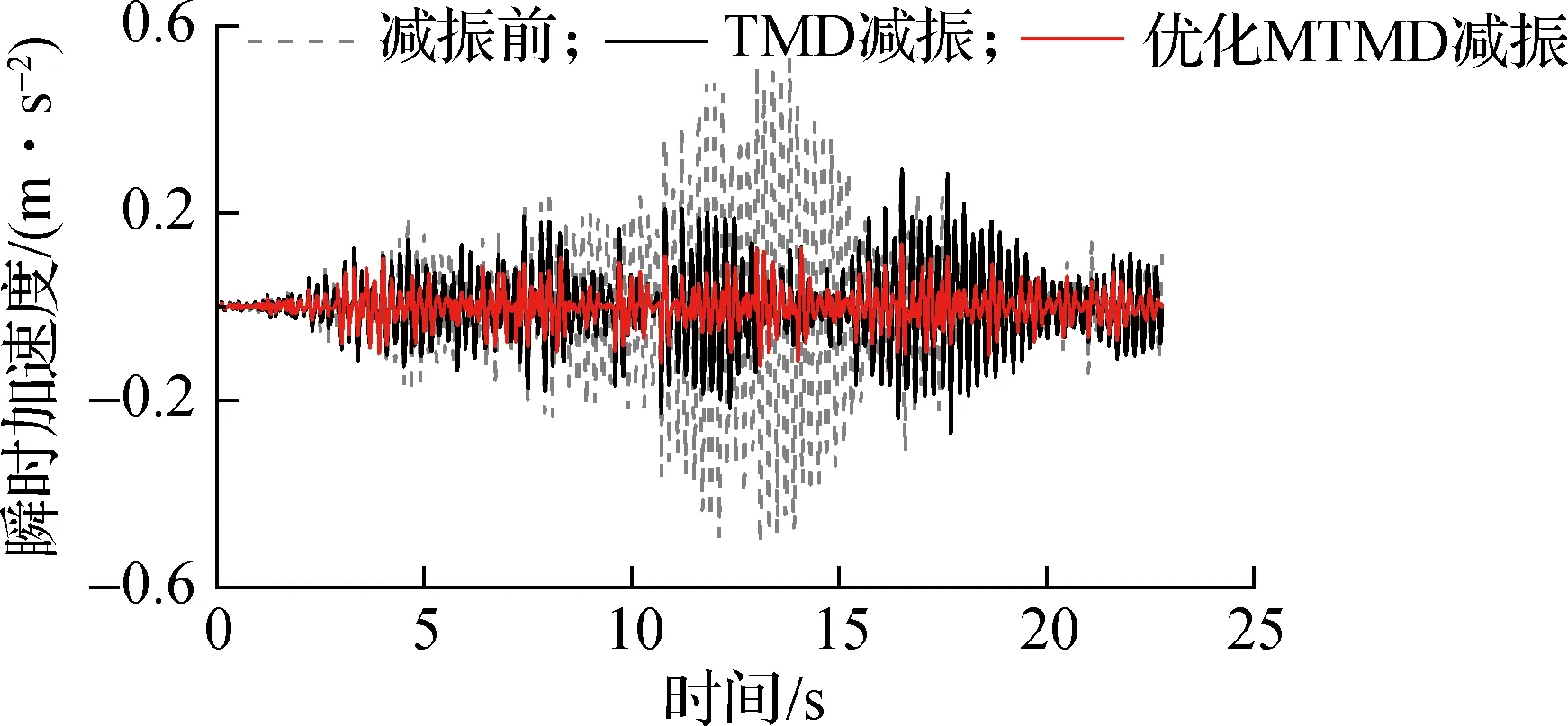
(f) 80人随机图6 结构中心减振前后加速度响应

表2 不同行走人数下结构减振前后峰值加速度

4 结论

1) 基于随机人群行走荷载模型建立的人群-大跨楼盖-TMD耦合动力学方程可以较好地反映人-结构相互作用与行人随机性.

2) 大跨楼盖上行走人数越多、模态质量越小,大跨楼盖的一阶瞬时阻尼比升高幅度越大,一阶瞬时频率降低幅度也越大.随着行走人数的增多,大跨楼盖加速度响应先增大后减小,行走人数为60时结构加速度响应达到最大值.相同行走人数下,模态质量越小,结构加速度响应越大.

3) 基于人-结构相互作用,建立了大跨楼盖MTMD减振优化设计方法.人群同步行走下与随机行走下大跨楼盖减振后的加速度响应均能达到楼盖舒适度要求,且优化MTMD的减振效果较单个TMD提升明显,最大提升率为46.36%.