考虑扭转与畸变耦联影响的薄壁箱梁翘曲效应分析

张元海 马云亮 刘泽翔

(1兰州交通大学土木工程学院, 兰州 730070)

(2兰州交通大学甘肃省道路桥梁与地下工程重点实验室, 兰州 730070)

薄壁箱梁广泛应用于现代桥梁工程中,其在竖向偏心荷载作用下的受力和变形状态非常复杂,在横截面上除了纵向弯曲产生的应力(正应力和剪应力)外,还有扭转、畸变及剪力滞翘曲效应引起的应力,而这些翘曲应力在弯曲应力中的占比往往是相当可观的,设计中不容忽视.

近年来,国内外许多学者针对薄壁箱梁的剪力滞、约束扭转及畸变效应开展了大量研究.郭增伟等[1]针对变截面悬臂箱梁,采用推广的比拟杆法研究其剪力滞效应,并通过参数分析揭示了变截面悬臂箱梁剪力滞效应的特殊性.舒小娟等[2]综合考虑箱梁全截面剪切变形影响,用Reissner最早提出的能量变分法分析箱梁的剪力滞效应.张元海等[3]考虑箱梁悬臂翼缘板与肋间板的横向变形差异性影响,提出了基于修正翘曲位移模式的剪力滞效应改进分析方法.张玉元等[4]研究了梗腋对箱梁剪力滞效应的削弱作用.在薄壁箱梁的约束扭转效应方面,Wang等[5]引入翘曲约束剪切扭转角作为广义翘曲位移,建立了约束扭转控制微分方程并给出初参数解.夏桂云等[6]和文颖等[7]用有限梁段单元分析箱梁的约束扭转效应,并通过插值函数直接求得翘曲扭矩,从而使剪应力计算大为简化.Li等[8]用有限梁段单元分析了单箱多室箱梁的约束扭转效应.为了便于计算约束扭转翘曲剪应力并克服部分文献中对剪应力计算的不合理性,张元海等[9]导出了计算约束扭转翘曲剪应力的2套实用公式,并从理论上论证了2套公式的统一性.在薄壁箱梁的畸变效应方面,Hansen等[10]研究了横截面的多种可能变形模式,能综合反映剪切变形、翘曲效应及横向泊松效应等影响.Ren等[11]分析了偏载作用下布置内横隔板箱梁的畸变效应,通过在横隔板与箱梁连接部位引入正交冗余力,充分反映横隔板与箱梁之间的相互作用.蔺鹏臻等[12]借助通用有限元软件计算了双线铁路简支箱梁在单线活载作用下的畸变效应.张元海等[13]通过在横截面畸变中心位置定义畸变角,利用能量变分法建立了畸变控制微分方程,并给出了广义内力和位移的初参数解.Cambronero-Barrientos等[14]用有限梁段单元分析了箱梁的剪力滞、约束扭转及畸变效应.

综上所述,目前在薄壁箱梁理论分析方面,主要是针对单一变形状态进行研究,不便于定量考察剪力滞、约束扭转及畸变翘曲应力在弯曲应力中的占比情况.此外,将箱梁所受偏心荷载分解为纵向弯曲、刚性扭转及畸变荷载并分别建立控制微分方程,本质上忽略了各基本变形状态间的耦联影响.本文综合考虑薄壁箱梁在竖向偏载作用下各基本变形状态,从而建立控制微分方程,放弃对外荷载的分解而直接表达结构总势能并应用变分原理,使扭转与畸变之间客观存在的耦联影响得到充分体现.

1 箱梁基本变形状态描述

本文分析的薄壁箱梁横截面如图1所示,O为横截面形心,x轴为水平形心轴,y轴为竖向对称轴,z轴沿梁轴方向,且x、y、z轴形成右手坐标系,y0为形心至顶板中面的距离;S和N分别为横截面扭转中心和畸变中心,yN为畸变中心N的y坐标;b1和b2分别为顶板和底板的半宽,b3为单侧悬臂板宽度,h为梁高,tt、tb和tw分别为顶板、底板和腹板的厚度,α为腹板水平倾角.

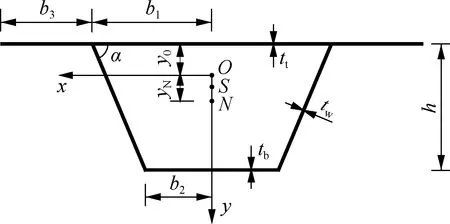
图1 箱梁横截面及坐标系

箱梁在竖向偏心荷载作用下,横截面内任一点处的纵向位移w(x,y,z)由4部分组成,即

w(x,y,z)=wb(y,z)+ws(x,y,z)+wt(z,s)+
wd(z,s)=-v′(z)y-f′(z)ωs(x,y)-
β′(z)ωt(s)-γ′(z)ωd(s)

(1)

式中,wb为初等梁的弯曲纵向位移;ws、wt、wd分别为剪力滞、约束扭转、横截面畸变引起的纵向翘曲位移;v为初等梁挠度;f为剪力滞附加挠度;β为与扭转角φ有关的约束扭转广义位移;γ为畸变角;ωs、ωt、ωd分别为相应于剪力滞、约束扭转及畸变的翘曲位移函数;s为沿壁厚中心线的坐标.

剪力滞翘曲位移函数ωs采用文献[3]建议的修正模式,即

(2)

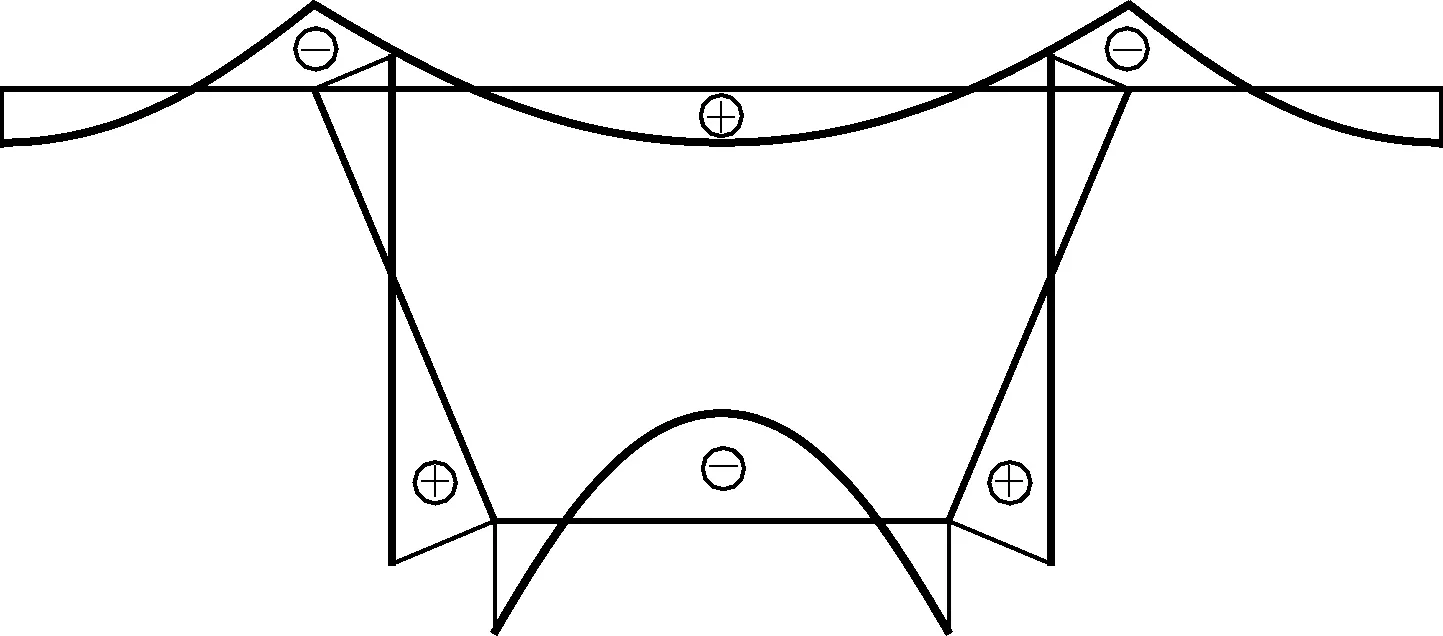
图2 剪力滞翘曲位移函数分布示意图

根据乌曼斯基第二理论,扭转翘曲位移函数ωt为

(3)

式中,ρS为从扭转中心S到周边任一点处切线的垂直距离;t为壁厚;ψ为相应于布雷特剪力流的扭转函数.

本文将横截面畸变角γ定义为过畸变中心N的水平线与y轴所形成直角的改变量[13],则畸变翘曲位移函数ωd为

(4)

(5)

式中,xN为横截面内过畸变中心N的水平线与两侧腹板交点之间距离的1/2;κ为取决于横截面尺寸的常数.

横截面内任一点处的畸变竖向挠度vd可通过畸变角γ表达为

(6)

(7)

式中,xw为计算点所在水平线与两侧腹板交点之间距离的1/2.

2 箱梁总势能

由式(1)可得箱梁相应于纵向正应变的应变能Uε为

(8)

式中,E为弹性模量;Ix为横截面对x轴的惯性矩;Iωs、Iωt、Iωd分别为相应于剪力滞、约束扭转及畸变的翘曲惯性矩;Iωtd为反映扭转与畸变耦联的惯性矩;l为跨度;F为横截面面积.

式(8)中各惯性矩的定义式为

相应于剪力滞的剪切应变能Uγs为

(9)

式中,G为剪切模量;Fs为剪力滞剪切面积[3].

与约束扭转剪应变γt相应的应变能Uγt为

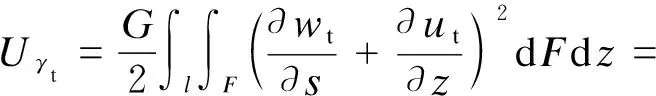
(10)

箱梁畸变时,由顶板、底板及腹板形成的横向闭合框架的应变能UR为

(11)

式中,K为畸变横向框架刚度[13].

竖向偏心荷载作用下,箱梁的外力势能Vp为

(12)

式中,p为分布竖向偏心荷载集度.

由式(8)～(12),可得箱梁总势能Π为

(13)

3 控制微分方程

对总势能式(13)进行一阶变分运算,可得

(14)

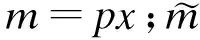
根据能量变分原理,结构在外力作用下处于平衡状态时,总势能的一阶变分等于零,故由δΠ=0,可得控制微分方程如下:

EIxv″″-p=0

(15)

EIωsf″″-η2GFsf″-p=0

(16)

GIρ(φ″-μβ″)+m=0

(17)

EIωtβ‴+EIωtdγ‴-GIρμ(β′-φ′)=0

(18)

(19)

方程(15)为纵向弯曲控制微分方程,方程(16)为剪力滞控制微分方程,方程(17)和(18)为约束扭转控制微分方程,方程(19)为畸变控制微分方程.方程(18)和(19)表明,约束扭转和畸变之间是耦联的,耦联刚度为EIωtd.

约束扭转控制微分方程(17)和(18)可以进行合并.当m沿跨度呈线性分布时,可得关于扭转角φ和畸变角γ的耦联微分方程为

(20)

当忽略约束扭转与畸变之间的耦联影响时,即当EIωtd=0时,则约束扭转微分方程(20)和畸变微分方程(19)就退化为现有文献中根据偏心荷载分解后推导的简单形式.

从式(14)中的边界项可得相应于各广义位移的广义力.例如,与扭翘广义位移-β′相应的扭翘双力矩Bωt为

Bωt=-EIωtβ″-EIωtdγ″

(21)

与畸翘广义位移-γ′相应的畸翘双力矩Bωd为

Bωd=-EIωdγ″-EIωtdβ″

(22)

联立求解式(21)和式(22),求得β″和γ″后易得扭翘正应力σωt和畸翘正应力σωd的计算公式为

(23)

(24)

扭翘剪应力τωt和畸翘剪应力τωd可通过箱壁微元体的平衡方程进行计算.

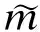
(25)

由式(20)和(25)消去γ,可得关于φ的八阶微分方程如下:

REφ(8)-μGIBEIωdφ(6)+KEIωtφ(4)-μGIBKφ(2)=μKm

(26)

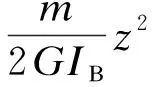
(27)

式中,C1～C8为积分常数;λ1～λ3为取决于扭转和畸变几何特性及材料弹性模量的系数.

再由式(20)和(25)消去γ″″,可得

(28)

将式(27)代入式(28)即可求得畸变角γ.积分常数C1～C8可根据梁端边界条件确定,本文不再赘述.

4 模型试验验证

文献[15]介绍了一个简支直线箱梁有机玻璃模型的试验情况,模型梁跨度l=2 m,横截面尺寸见图3.梁端设有横隔板,其板厚均为6 mm.材料弹性模量为2 943 MPa,泊松比取0.4.竖向偏心集中荷载P=98.1 N作用于跨中截面单侧腹板与顶板相交处.共测试l/8、3l/16、5l/16、7l/16、l/2及13l/16六个横截面处的正应力分布,应力测点具体位置见图3中①～⑥.试验详细情况见文献[15].

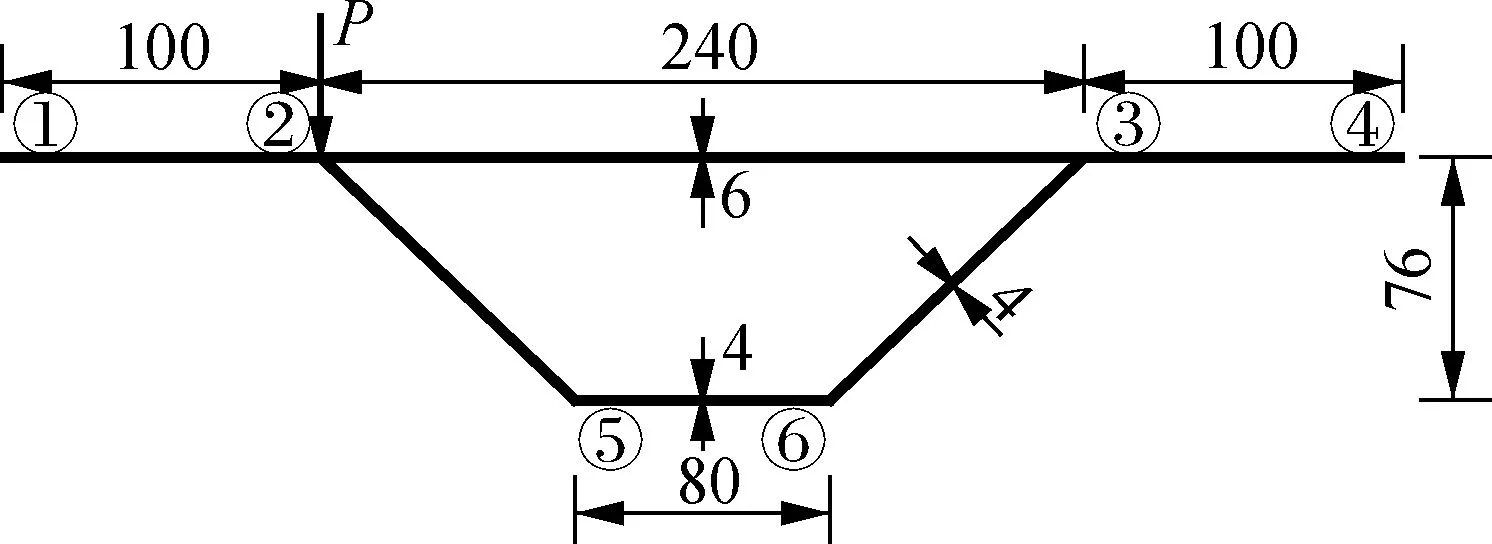
图3 模型梁横截面简图(单位: mm)

计算表明,考虑扭转与畸变耦联的计算结果与传统方法计算结果相差不大,而计算工作量大增,从实用计算考虑,可略去耦联影响.将7l/16截面各测点处正应力理论值连同实测值一并列于表1,其中σb为纵向弯曲应力,σs为剪力滞翘曲应力,σωt为扭转翘曲应力,σωd为畸变翘曲应力,σ为总应力,应力以拉为正、压为负,应力实测值是在文献[15]中实测应力分布曲线上按比例量取的.由表1可知,总应力理论计算值与实测值总体上吻合良好.

表1 7l/16截面各测点处正应力比较 kPa

从表1还可以看出:竖向弯曲应力在总应力中占绝对主导地位,剪力滞、约束扭转及畸变翘曲应力总体上都很小;而在这3种翘曲应力中,剪力滞翘曲应力最小,畸变翘曲应力最大;畸变翘曲应力最大值位于腹板与底板交接处,在顶板和悬臂板内都很小;约束扭转翘曲应力在底板内很小,其最大值位于悬臂板自由端.

5 算例分析

预应力混凝土简支箱梁计算跨径l=30 m,采用C50混凝土,材料弹性模量E=34.5 GPa,剪切模量G=13.8 GPa,仅在梁端设有横隔板,竖向偏心荷载P=550 kN作用于跨中截面左侧腹板顶部,跨中截面尺寸如图4所示.

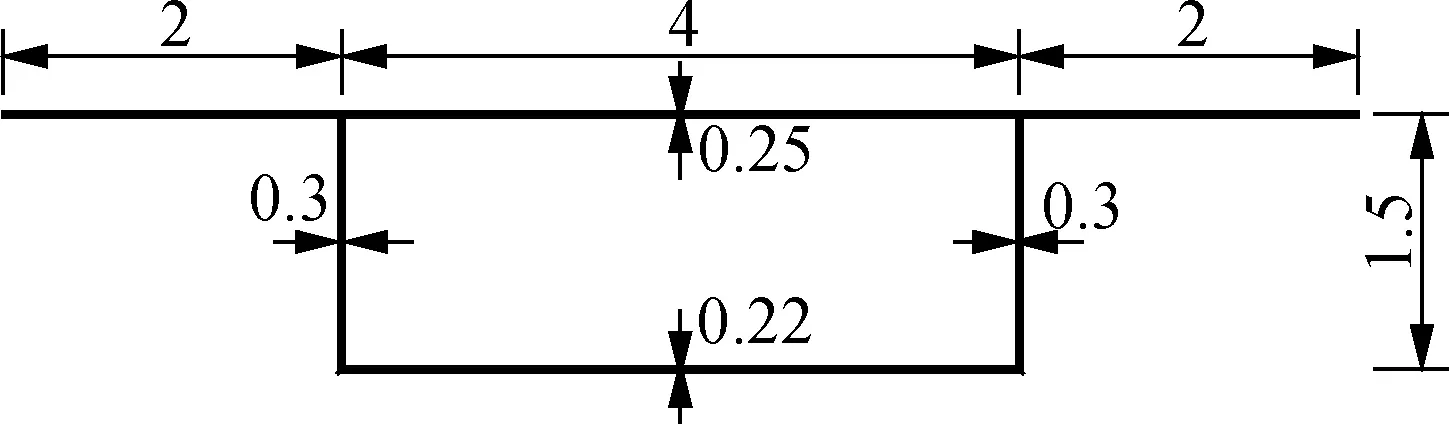
图4 简支箱梁横截面(单位: m)

按本文方法求得跨中截面纵向弯曲正应力、各翘曲正应力及总应力分布图如图5所示.由图可见:纵向弯曲正应力占绝对主导地位;由于约束扭转与横截面畸变影响,施加偏载一侧的腹板比另一侧腹板的总应力大很多,两侧腹板与底板交点处的总应力相差最为悬殊,相差达1.24倍,即(4 076.84-1 818.05)/1 818.05=1.24;在腹板与底板交点处,畸变翘曲应力最大,约束扭转翘曲应力最小.

(a) 纵向弯曲正应力

(b) 剪力滞翘曲正应力

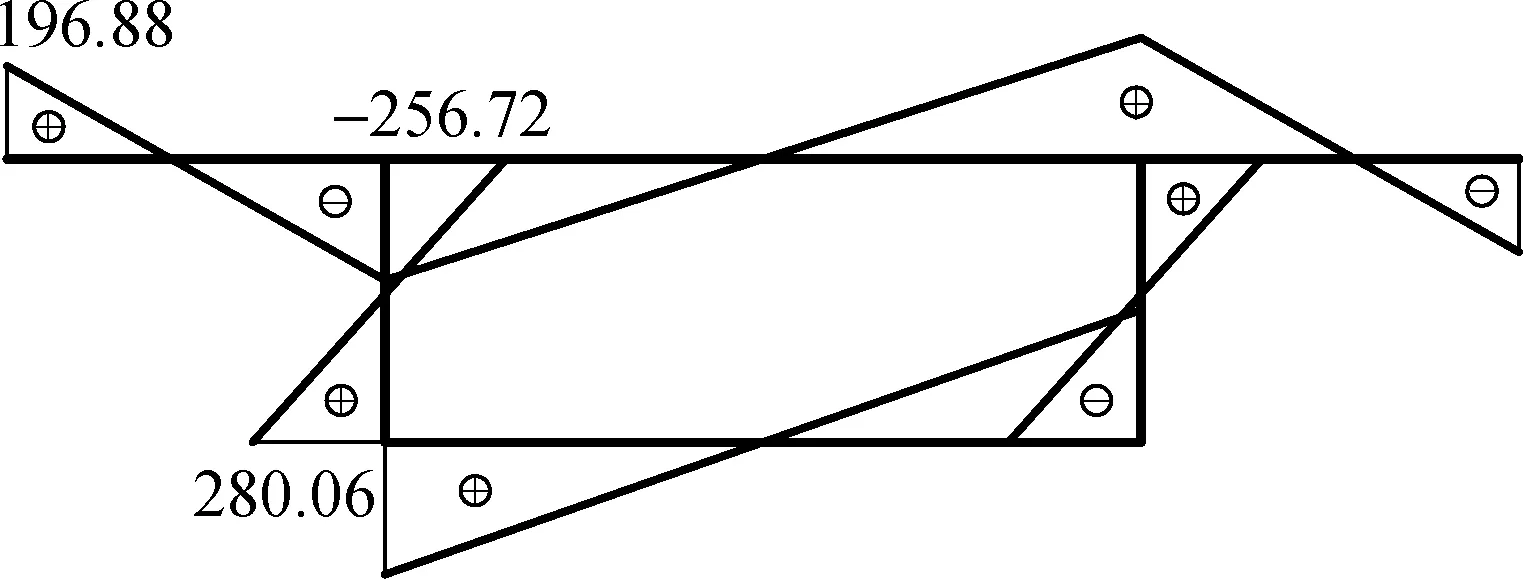
(c) 扭转翘曲正应力

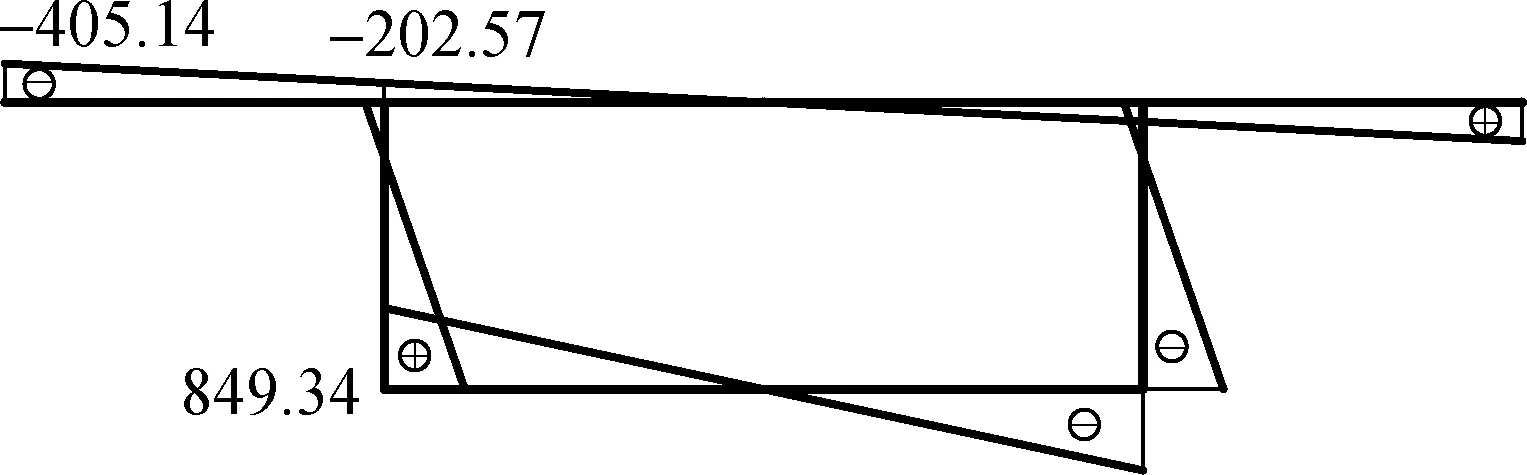
(d) 畸变翘曲正应力

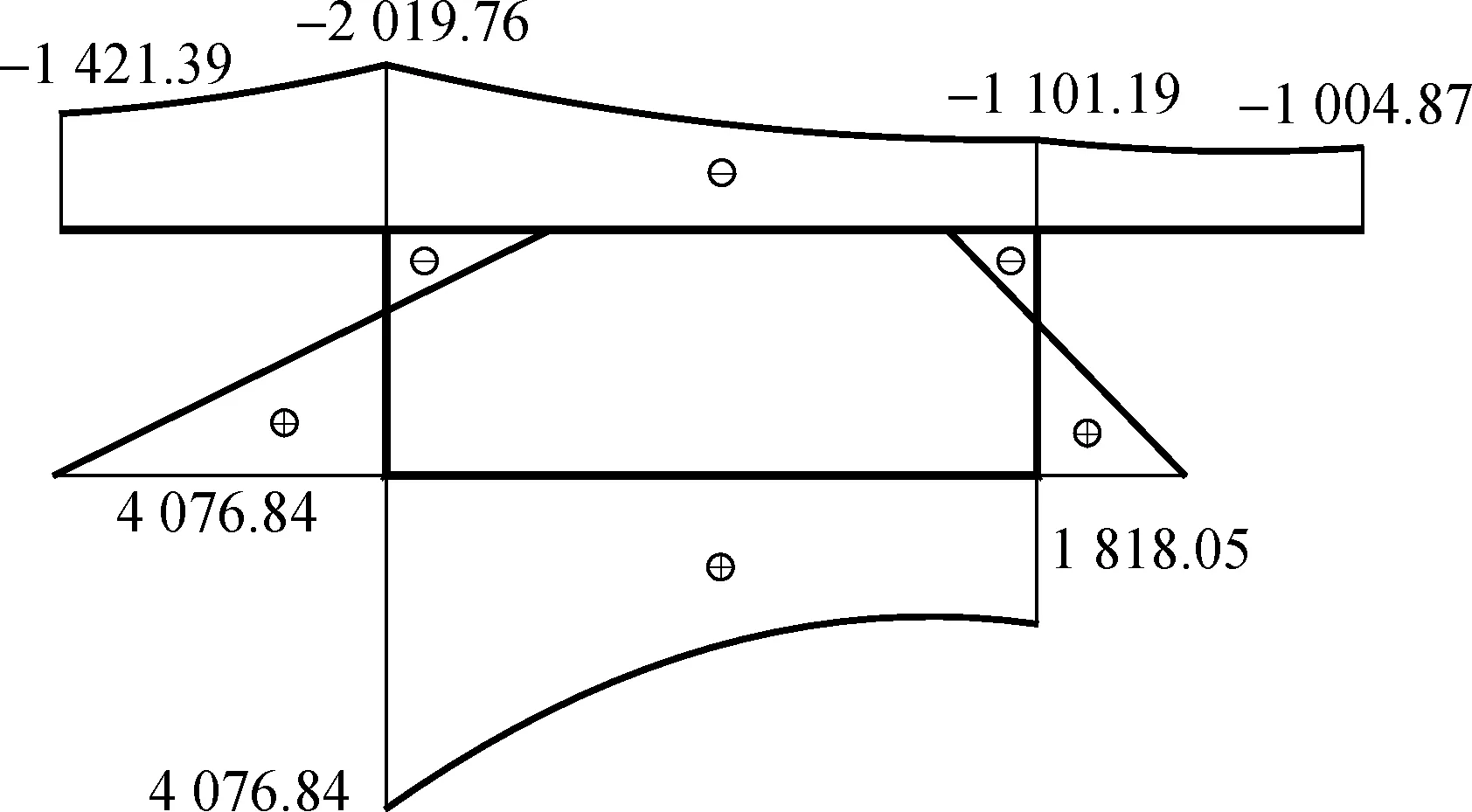
(e) 总应力

图6显示了跨中左截面的剪应力分布图,图中用箭头示出了剪应力方向,剪应力以围绕周边逆时针方向为正,顺时针为负.

由图6可以看出:2块腹板内的总剪应力相差特别显著,施加偏载一侧的腹板内最大剪应力约为另一侧腹板内相应剪应力的10倍,而且方向相反;剪力滞翘曲剪应力在腹板内总体上很小,实用计算中可以忽略,但其在底板内靠近两侧处仍相当可观,最大值甚至超过了腹板内的最大弯曲剪应力,不容忽视;约束扭转和畸变翘曲剪应力在每块腹板内都很大,而且方向相同,但由于2块腹板内的扭转和畸变翘曲剪应力方向正好相反,故导致腹板内剪应力发生显著的重分布;畸变翘曲剪应力在底板内最大,其与剪力滞翘曲剪应力一起,使底板内产生较大的总剪应力,可能会导致底板产生贯通的面内斜裂缝,设计中应重视.

(a) 纵向弯曲剪应力

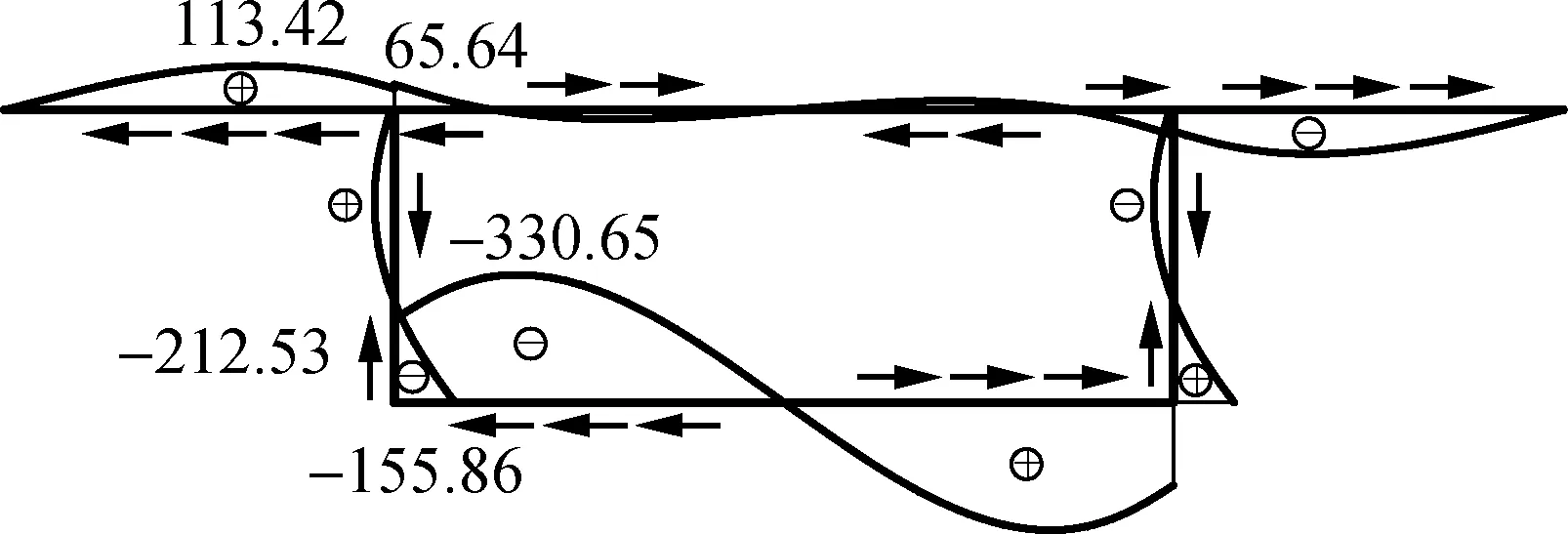
(b) 剪力滞翘曲剪应力

(c) 扭转翘曲剪应力

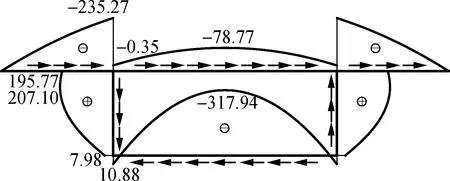
(d) 畸变翘曲剪应力

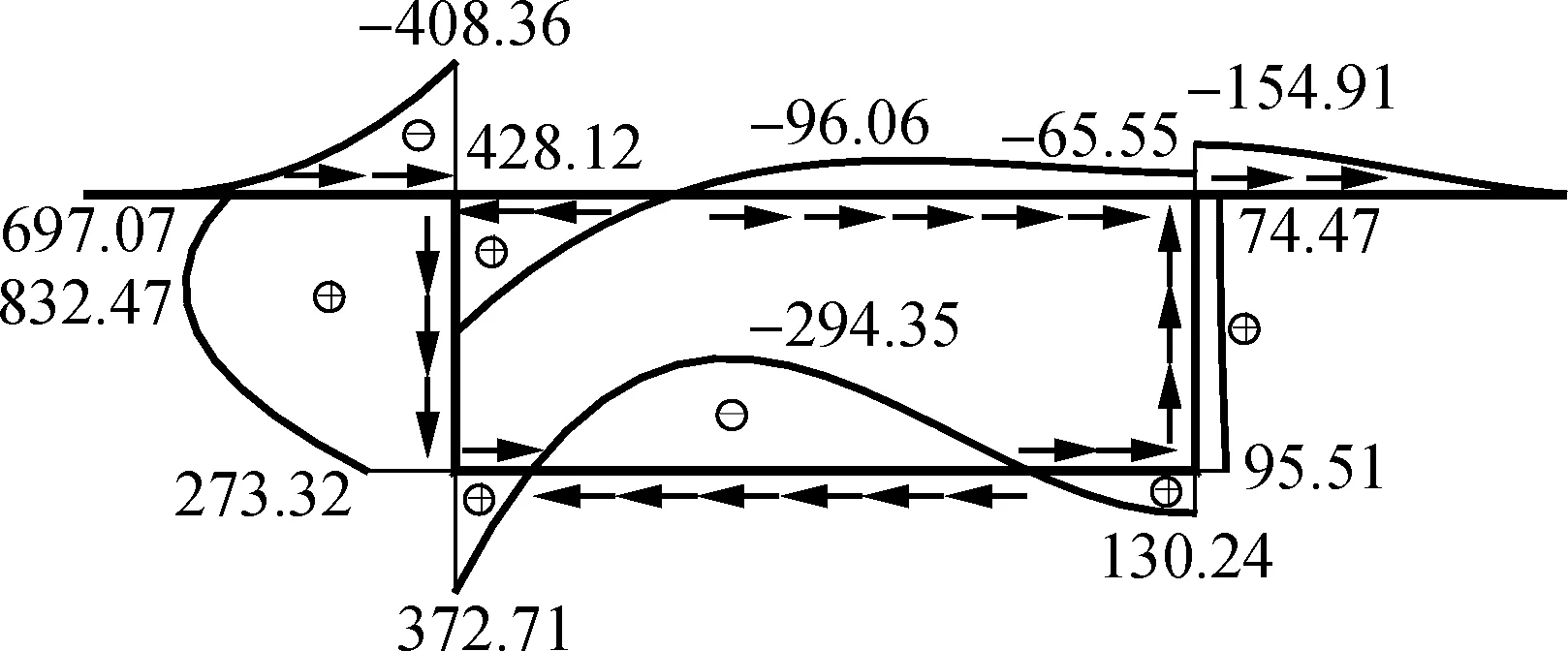
(e) 总应力

为了考察横截面关键点处由剪力滞、约束扭转及畸变翘曲应力引起的相对于弯曲应力的应力放大系数,表2列出了跨中截面受偏载直接作用的腹板与顶、底板交点处各项正应力大小及其相对于弯曲应力σb的占比情况.

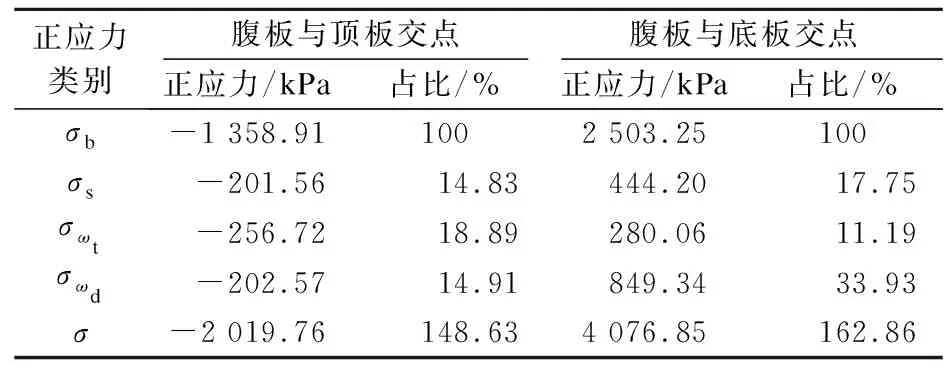
表2 跨中截面加载腹板与翼缘板交点正应力

由表2可知,在加载腹板与底板交点处,畸变翘曲应力为弯曲应力的33.93%,总应力达到弯曲应力的162.86%,即总应力放大系数约为1.63.在加载腹板与顶板交点处,约束扭转翘曲应力为弯曲应力的18.89%,总应力放大系数约为1.49.

表3列出了跨中左截面受偏载直接作用的腹板在横截面形心轴处的各项剪应力及其相对于弯曲剪应力的占比情况.其中,τb为纵向弯曲剪应力,τs为剪力滞翘曲剪应力,τωt为约束扭转翘曲剪应力,τωd为畸变翘曲剪应力,τ为总剪应力.

表3 跨中左截面形心轴处加载腹板的剪应力

由表3可知,在横截面水平形心轴处,受偏载直接作用的腹板的约束扭转翘曲剪应力达到弯曲剪应力的78.39%,畸变翘曲剪应力达到弯曲剪应力的60.99%,而总剪应力甚至达弯曲剪应力的254.85%,即总剪应力的放大系数约为2.55,表明约束扭转和畸变翘曲剪应力对总应力的贡献非常大.

值得指出的是,在《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG3362—2018)中,对于单梁模型的应力放大系数计算公式中,只关注箱梁的约束扭转翘曲应力影响,并未包含畸变翘曲应力,显然这是偏于不安全的.

6 结论

1) 本文综合考虑薄壁箱梁在竖向偏载作用下的剪力滞、约束扭转及畸变翘曲效应影响,放弃外荷载分解的传统思路,在充分考虑扭转与畸变耦联影响的基础上,用能量变分法建立了控制微分方程,通过对一有机玻璃模型梁的计算表明,本文理论计算结果与模型试验结果吻合良好,验证了本文理论分析的正确性.

2) 薄壁箱梁在竖向偏心荷载作用下,纵向弯曲是最主要的变形状态,畸变和约束扭转是起主导作用的翘曲变形状态,剪力滞变形状态总体上属于次要的翘曲变形状态,但剪力滞效应对弯曲正应力的影响仍不可忽略.在底板两侧一定范围内的剪力滞翘曲剪应力也需引起注意.

3) 本文简支箱梁算例考虑剪力滞、约束扭转及畸变翘曲效应影响后,在跨中截面加载腹板与底板交点处的正应力放大系数达到约1.63,在形心轴处腹板的剪应力放大系数达到约2.55,在设计中需引起高度重视.

4) 薄壁箱梁在竖向偏载作用下具有复杂的受力性能,在跨内不设横隔板的情况下其畸变变形状态尤为突出,不容忽视.而《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG3362—2018)在对于单梁模型的应力放大系数计算公式中,只关注箱梁的约束扭转翘曲应力影响,却并未包含畸变翘曲应力,这是值得商榷的,也偏于不安全.