混合公交系统的票价和服务区域协同优化

郭蓉蓉 刘人铭 余静财 张 进 李文权,3

(1东南大学交通运输学院, 南京 211189)

(2丹麦技术大学技术、管理和经济学院, 哥本哈根 2800)

(3东南大学城市智能交通系统江苏省重点实验室, 南京 211189)

公共交通是城市交通发展的重要基础设施之一,发展公共交通是引领未来城市交通可持续发展的必要措施.按照服务模式和特点,城市公交系统一般被分为固定公交服务(fixed-route transit, FRT) 和需求响应式公交服务 (demand-responsive transit, DRT)两大类.FRT采用固定的运行模式,而DRT允许车辆偏离固定设置,进而改善乘客可达性[1].DRT服务的优势在于灵活性[2],但其平均运营成本相较于FRT服务更高[3].因此,为了综合发挥这2种公交服务的优势,研究者们采用混合公交系统设计,即将DRT的灵活性与FRT的低成本性相结合.

目前,根据服务范围的差异,混合公交系统设计主要分为区域型[4-5]和线路型[6]两大类.在区域型设计的混合系统中,Stein[4]将整个服务区划分为若干子区域,在各子区域间和子区域内分别运行FRT和DRT,乘客可以在一个子区域内使用DRT到达换乘点后,乘坐FRT前往另一个子区域.Aldaihani等[5]设定一个子区域内的DRT车辆仅在该子区域内运行,并服务该子区域内的所有乘客,不同子区域内的DRT车辆不能跨子区域运行.在线路型设计的混合公交系统中,DRT以FRT线路为基准线,并与 FRT运行前进方向相同.Chen等[6]将线路型混合公交系统称为需求适应式双线混合公交系统(demand adaptive paired-line hybrid transit, DAPL-HT),并将 DRT设计成仅为从出发地/目的地到最近换乘站距离超过一定阈值的乘客提供服务.与区域型混合公交系统不同,线路型混合公交系统中的DRT系统可以在整个服务区中运行而不是仅限制在一个子区域,且不能为整个服务区内的所有乘客提供服务.Chen等[7]证实了在多种测试场景下,线路型混合公交系统在运营商和用户成本方面均优于区域型混合公交系统.

公交票价在各种类型的公交系统中都是公交机构的一个重要设计参数.常用的票价策略包括单一票价[8]、基于距离的票价[9]、基于时间的票价[10]、基于服务的票价[11]及分段票价[12]等.现有关于公交定价的研究主要集中在FRT的定价上,对DRT的定价[13]研究较少,针对混合交通系统中关于DRT的定价研究更是鲜有报道.由于DAPL-HT系统中涉及不同类型的公交车,因此在制定票价策略时应考虑乘客乘坐的不同公交服务.在给定的票价策略下,确定最优公交票价的常用方法包括双层规划[12]、混合整数非线性规划(MINP)[10]、混合整数线性规划(MINP)[14]、非线性规划(NLP)[8]、线性规划(LP)[15]和连续近似(CA)[16]等.这些规划模型优化目标一般包含用户成本、运营商收益和社会福利等,且根据实际需求,可构建单目标或多目标模型.此外,公交票价也可以与其他影响运营商利润和乘客出行成本的变量同时优化.混合公交系统中,若在乘客距离固定站点较近的情况下仍选择DRT服务而不是步行到达固定站点乘坐FRT车辆,可能会增加乘客的总出行时长,也可能增加系统的运行成本.因此,仅允许DRT服务于从出发地/目的地到最近固定站点/换乘点的距离超过一定阈值的乘客,起终点在阈值内的乘客需步行到达固定站点或目的地.

为推进发展基于线路的混合公交系统,本文对系统中DRT线路票价和DRT/FRT公交的服务区域进行协同优化.以DAPL-HT系统为研究对象,以用户成本最小为目标,以运营商非负收益为约束,采用连续近似和非线性规划方法同时优化DRT票价和整个服务区域中FRT/DRT的服务区域.研究结果可为混合公交系统的运行和管理提供科学依据和理论支撑,促进建立高品质的城市公交系统.

1 系统描述

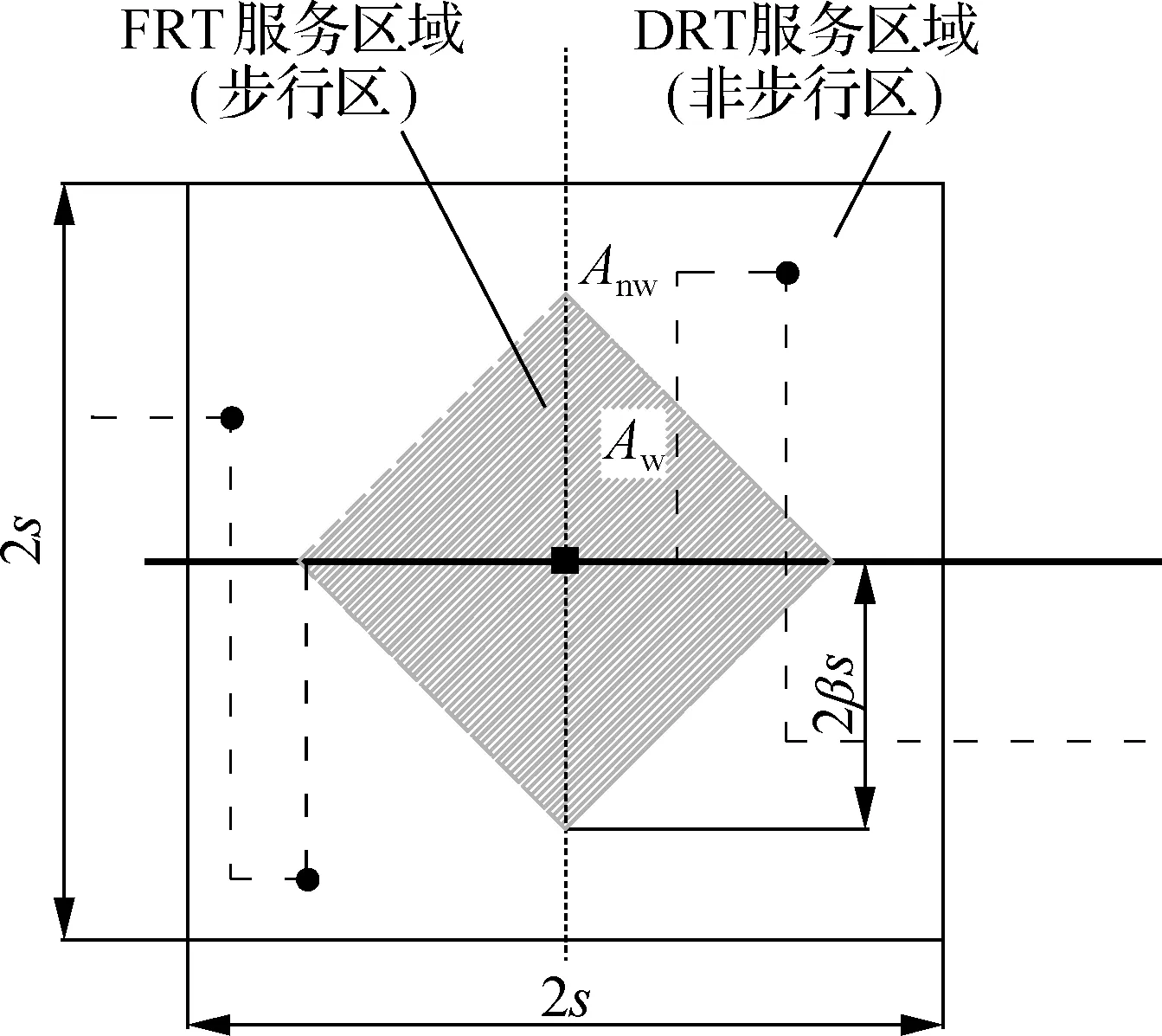
本文采用线性走廊来模拟近似的道路网络[17].如图1所示,整个服务区长度为D,宽度为2s.服务于矩形区域的DAPL-HT系统由FRT和DRT组成.其中,FRT为基准路线,线路长度为D,做直线往返运行;而DRT以FRT线路为基准路线,根据研究区域内的用户需求,在临时站点接载乘客,车辆被允许偏离基准路线的最大距离为s.整个研究区域被划分为n个方形子区域,对应n个站点,nk为第k个子区域的固定站点.相邻车站之间的距离为2s,因此n=D/(2s).令DAPL-HT系统中FRT和DRT的车头时距分别为H1和H2,公交车辆的平均行驶速度为vb.

DAPL-HT系统仅为起终点离固定站点超过一定距离的乘客服务,该距离阈值为2sβ(β∈(0,1]).若某乘客与固定站点的距离小于该阈值,则无法乘坐DRT车辆,须步行到固定站点乘坐FRT车辆;反之,该乘客可以使用DRT服务.该距离阈值内的区域称为步行区或FRT服务区域,之外的区域称为非步行区或DRT服务区域.因此,2种公交服务边界由参数β和DRT的最大偏移距离s决定.

2 模型构建

2.1 模型假设

基于系统描述,为建立优化模型,提出如下假设:

1) 整个服务区内单位小时单位面积产生的需求密度为λ,乘客的起终点在服务区内是均匀独立分布的[6].

2) 存在一个控制中心负责收集乘客的请求并实时调度DRT车辆,FRT车辆则按照既定时刻表定点定线运行.

3) 当一辆DRT车辆在第k个子区域内行驶时,控制中心接收并处理来自第k+1子区域的乘客请求(见图1).第k+1子区域内请求处理完后,DRT车辆将运行至站点nk+1,按照此过程依次处理后续子区域内的需求.

图1 DAPL-HT示意图

4) 控制中心根据当前DRT车辆剩余容量,确认其能处理的请求集,将额外请求传递给车队中的下一辆车.若在一个子区域内没有DRT服务需求,DRT车辆则按照FRT线路运行.

2.2 运营商和用户成本

2.2.1 车辆运行成本

单位小时内DAPL-HT系统的运营成本取决于总体运行距离和车队规模[6].公交车的期望运行距离是平均往返距离与相应车头时距的比值.FRT仅沿直线做横向往返运行,往返距离为2D,则FRT单位小时内的预期行驶距离d1=2D/H1.DRT车辆每次往返的总距离包括横向和纵向距离,显然 DRT车辆运行的横向距离与FRT车辆的往返距离相同,而纵向距离则取决于服务需求量.本文采用文献[18]中方法计算纵向距离,单个DRT乘客的期望纵向距离为 2s/3,往返1次沿途产生的乘客人数为2DsλH2,考虑DRT车辆仅接送DRT服务区域产生的乘客需求,设DRT服务区域面积占总区域面积的比例为a2,则DRT单位小时的平均行驶距离d2=2D/H2+4Ds2λa2/3.

公交车车队规模为单位小时内运行的车辆数.运行DAPL-HT系统所需的车队包括FRT车队数量m1和DRT车队数量m2.设τ1和τ2分别表示FRT和DRT接送乘客的驻站时间.在FRT运行过程中,行驶预期距离d1的时间包括平均行驶时间d1/vb和驻站时间2nτ1/H1[19],则FRT的车队数量m1=d1/vb+2nτ1/H1.在DRT运行过程中,行驶预期距离d2的时间包括平均行驶时间d2/vb和驻站时间4τ2Dsλa2[6],则DRT的车队数量m2=d2/vb+4τ2Dsλa2.

综上可知,单位小时DAPL-HT系统的运行成本为

Zoper=cm(m1+m2)+cd(d1+d2)

(1)

式中,cm和cd分别为公交车行驶时间成本和距离成本.

2.2.2 用户出行成本

用户出行成本包括用户出行时间成本[20]和支付的票价.为计算各成本构成,首先将所有乘客根据不同的车辆服务分为3种类型;然后,分别计算每种乘客类型的用户成本;最后,采用连续近似法,得到单个乘客的总用户成本.

在DAPL-HT系统服务区域内出行的乘客,根据其起终点位置和出行服务,可分为以下3种类型:① 起点和终点都在步行区内,出行行程仅乘坐FRT;② 起点/终点位于步行区内,终点/起点位于步行区外,出行行程分别乘坐FRT 和DRT车辆各1次;③ 起点和终点都在非步行区,出行先乘坐DRT换乘FRT再换乘DRT,即乘坐2次DRT和1次FRT.令3类乘客所占比例分别为p1、p2和p3,且p1+p2+p3=1.

基于假设,乘客出行的起终点在整个服务区中均匀分布.乘客的起终点在FRT 和DRT服务区域内的概率即为FRT和DRT服务区域面积占总区域面积的比例a1和a2,可分别由相应区域的面积Anw和Aw近似表示.如图2所示,当β∈(0,0.5]时,a1=2β2;当β∈(0.5,1]时,a1=1-2(1-β)2.2种情况下均有a2=1-a1.因此,基于乘客类型的划分标准,3类乘客所占比例分别为

(a) β∈(0,0.5]

(b) β∈(0.5,1]

(2)

p2=a1a2+a2a1

(3)

(4)

步行区边界越大,使用FRT服务的乘客数量越多,使用DRT服务的乘客数量越少.即β值越大,FRT服务区域面积越大,DRT服务区域面积越小.此外,随β值的增大,类型1乘客所占比例单调递增,而类型3乘客所占比例单调递减,类型2乘客所占比例先增大后减小.

本文设计的系统中仅考虑单条FRT线路和单条DRT线路,不涉及多条FRT线路之间的换乘.为简化分析,参考文献[6],暂不考虑FRT与 DRT之间的换乘时间.因此,本文研究的单用户出行时间成本构成包括平均步行时间、平均等待时间和平均乘车时间.

乘客的平均步行时间根据其步行距离计算.在整个出行过程中,需要步行的路段包括起点至固定站点和固定站点至终点2段.因此,类型 1 乘客有2段步行,类型 2 乘客仅有1段步行,而类型3 乘客无需步行.以图2所示的2种情况为例,仅考虑第1象限,当β∈(0,0.5]时,平均步行距离是指从步行区的质心到固定站点的距离,该距离可等同于质点到固定站点2个方向的垂直距离之和.以固定站点为坐标轴原点,由于乘客的起终点在服务区内均匀独立分布,垂直距离可基于步行区的3个顶点坐标得出,因此3类乘客的平均步行时间分别为

E1=8sβ/(3vp)

E2=4sβ/(3vp)
E3=0

式中,vp为乘客的平均步行速度.

当β∈(0.5,1]时,FRT服务区域面积Anw=2s2(1-β)2,DRT服务区域面积Aw=s2-Anw.设第1象限中步行区和非步行区的质心到固定站点的距离分别为lAw和lAnw.基于DRT服务区域3个顶点坐标可直接得出lAnw=2(2sβ+s)/3,并根据对称性和方形网格质心间接求得lAw=[s(Anw+Aw-AnwlAnw)]/Aw,则3类乘客的平均步行时间为

E1=2lAw/vp

E2=lAw/vp

E3=0

由此可知,单个乘客的平均步行时间为

E=E1p1+E2p2+E3p3

(5)

平均等待时间一般可用1/2车头时距来近似计算[5-6].对于类型1 乘客,由于其只使用FRT服务,仅在起始的固定站点等待FRT车辆,故平均等待时间W1=H1/2.类型 2乘客分别乘坐FRT车辆和DRT车辆各1次,则其平均等待时间W2=H1/2+H2/2.类型3乘客需要在起始临时站点乘坐DRT,起始固定站点换乘FRT和终点固定站点换乘DRT,则其平均等待时间W3=H1/2+H2.因此,单个乘客的平均等待时间为

W=W1p1+W2p2+W3p3

(6)

平均乘车时间为平均乘车距离与车辆速度的比值.为计算不同类型乘客的期望乘车距离,需分别计算FRT和DRT车内乘客的平均乘车距离.本文采用文献[5]方法计算FRT乘客平均乘车距离,将整个矩形服务区分为n个子区域 (见图1),系统中乘客随机选择上下车站点的集合表示为N={(p,q)},p≠q,p,q∈{1,2,…,n},dn为n个子区域集合N的累积距离.因此,FRT车内乘客的平均乘车时间为

(7)

对于DRT乘客平均乘车时间,与计算平均步行时间的方法类似.当β∈(0,0.5]时 ,在DRT服务区域(非步行区)的乘客,起点/终点与固定站点之间的平均纵向距离l=(3s-8sβ3)/[6(1-2β2)];当β∈(0.5,1] 时,平均纵向距离l=(2βs+s)/3.由于DRT运行涉及到偏移距离和乘客数量,无法直接计算,本文假设DRT行程总距离与运行横向距离的比值ρ=d2H2/(2D)和乘客平均乘车距离与总乘车距离的比值相同.则DRT车内乘客的平均乘车时间为

(8)

同理,参考平均等待时间的分析,3类乘客的平均乘车时间分别为

T1=t1

T2=t1+t2

T3=t1+2t2

因此,平均单个乘客的平均乘车时间为

T=T1p1+T2p2+T3p3

(9)

2.2.3 票价成本

由于DAPL-HT系统中包含2种公交服务,不同类型乘客所选择的出行路线不同,因此采用单一的票价策略是不合理的.在DAPL-HT系统中,各类乘客选择乘坐的公交服务频次不同,考虑公交公益性的前提下,基于服务路线和乘车频次不同,为3类乘客制定如下票价策略:类型1乘客仅支付FRT基本票价;类型2乘客仅支付DRT基本票价;类型3乘客支付FRT和DRT基本票价.采用连续近似方法,单个乘客的平均票价计算为

F=f1(p1+p3)+f2(p2+p3)

(10)

式中,f1为FRT票价;f2为DRT票价.

2.3 非线性优化模型

本研究旨在确定整个研究区域中2种公交的最佳服务边界,并为使用混合系统的乘客制定一种票价策略,在考虑运营商收益非负的约束条件的同时,使用户总成本最小化.根据国内多数城市的普遍设定,对FRT服务采用给定的统一票价;而对于DRT服务,其票价将由优化模型确定.运营商收益是总票价收入和运营成本之间的差额,前者取决于服务的乘客数量和票价,后者由每小时内车辆的运行距离和车队数量来决定.由于乘客请求是否会被服务受制于DRT服务区域面积的大小,故将服务区域边界参数β设定为决策变量.在运营商的运行成本中,FRT和DRT的运行距离和车队数量计算公式均为非线性运算.在用户的出行成本中, 3类乘客所占比例计算公式为非线性运算,单个乘客的步行、等待、乘车和票价成本均采用连续近似方法得到,故用户成本计算公式也为非线性运算.基于目标和约束条件,构建非线性优化模型为

minZuser(β,f2)=(γEE+γWW+γTT)ctime+γFF

(11)

s.t.

2λDsF-Zoper≥0

(12)

0<β≤1,fmin≤f2≤fmax

(13)

式中,目标函数Zuser为单个乘客出行总成本;γE、γW、γT、γF分别为乘客步行时间、等待时间、乘车时间和票价成本的指标系数,此处均默认为1;ctime为乘客出行时间时间成本转换为货币价值的时间价值;fmin、fmax分别为票价最低值和最高值.

3 数值实验

针对涉及不等式约束的非线性规划问题,通常可采用启发式算法求解,如遗传算法[7]等.考虑到优化模型中决策变量维度较小,相较于启发式算法,枚举法能以较小的增量间隔列举决策变量的所有可能组合,从而更精确地找出满足约束条件的最优解.因此,本节运用枚举法来设计数值实验,优化模型求解结果,并通过灵敏度实验进一步分析关键输入参数变化对结果的影响.

3.1 参数设置

在长度D=10 km的线性走廊中运行DAPL-HT系统,国内每小时内公交车的发车频次一般为6～7辆,因此设定FRT和DRT的车头时距均为0.15 h.基于国内大多数城市的票价,决策变量DRT票价范围设定为fmin=2元,fmax=20元.时间价值参数参照地区每小时收入设置,ctime=20元/h.DRT车辆偏离基准线路(FRT线路)的距离一般为0.4～1.2 km,设定s=0.6 km.其他参数参考文献[6,19]设置如下:需求密度λ=10～100 人/(h·km2),车辆运行速度vb=25 km/h,乘客步行速度vp=5 km/h,FRT驻站时间τ1=12 s,DRT驻站时间τ2=13 s,FRT票价f1=2元,每辆公交车行驶时间成本cm=40元/h,每辆公交车行驶距离成本cd=4元/km.

3.2 优化结果

图3给出了不同决策变量β和f2组合下的用户成本和运营商收益.由图可知,无论是在低需求密度(λ=10 人/(h·km2))还是高需求密度(λ=100 人/(h·km2))下,当β值不变时,3类乘客所占比例不变,随着DRT票价的增高,用户成本逐渐增加.随着β值的增大(即FRT的服务区域面积相较于DRT变大),乘坐低成本固定线路公交的乘客增加,此时较低的DRT票价即可满足运营商收益非负的约束条件,从而降低了用户成本.用户成本随着β值和票价的增大表现出不同的变化趋势,呈非单调性变化.

(a) 低需求水平下用户成本

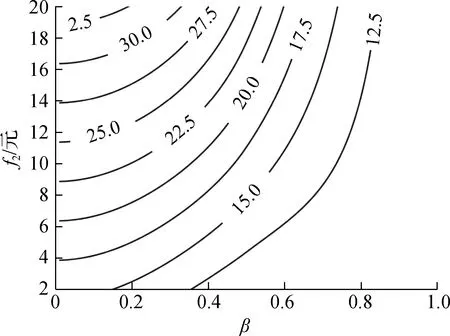
(b) 高需求水平下用户成本

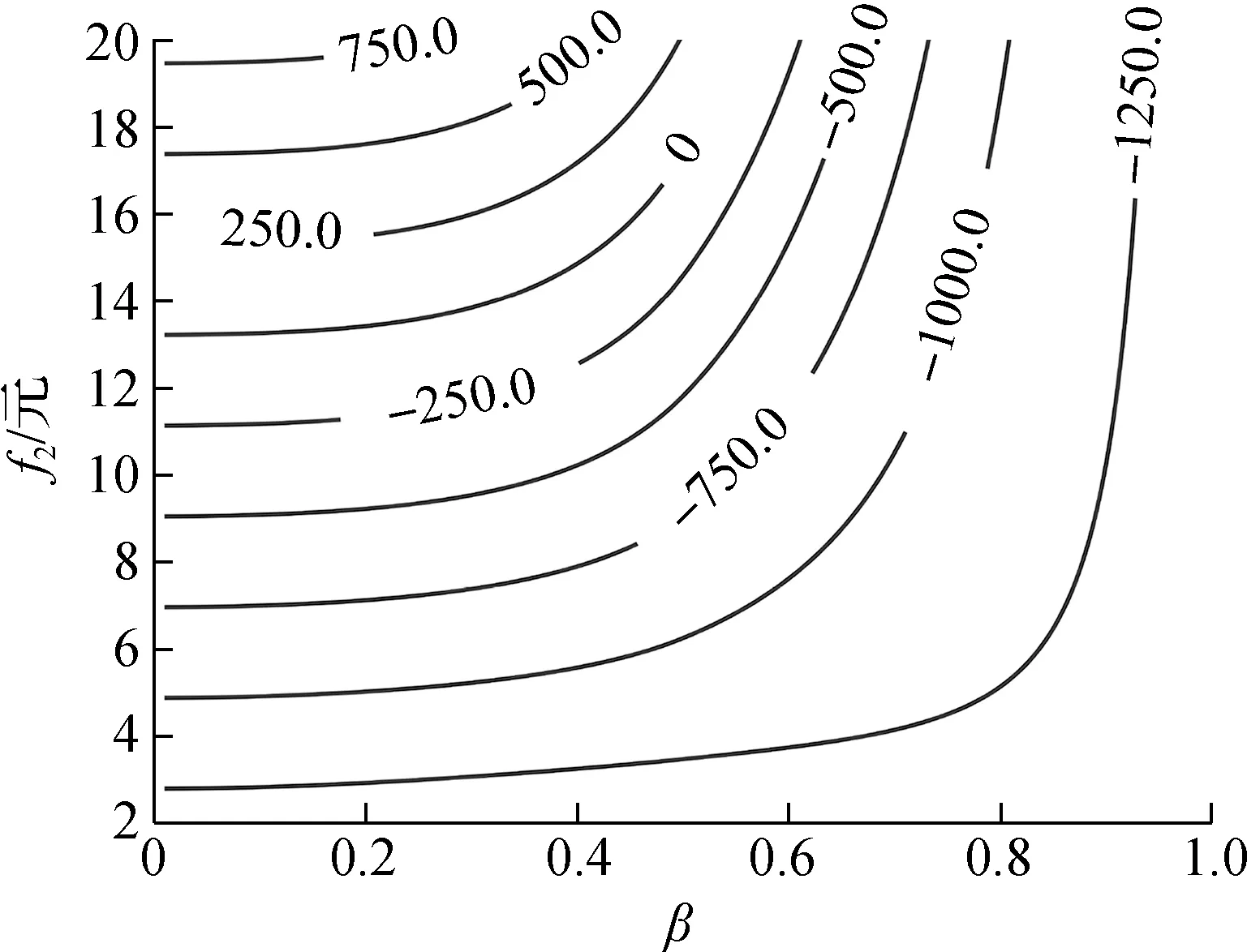
(c) 低需求水平下运营商收益

高需求密度下的运营商收益远大于低需求密度.因此,在低需求水平下,考虑到优化模型的约束条件,需要在所有可能组合中筛选掉运营商收益为负的决策变量组合,将剩余结果中满足式(11)的决策变量组合作为最优解.当需求密度较高时,所有组合的运营商收益均大于零,模型最优解在最小目标值处获得.

图4(a)给出了不同需求密度下2个决策变量的最优组合.由图可知,最优DRT票价值随乘客需求密度的增加逐渐减少,而DAPL-HT中FRT和DRT的服务区域边界参数β受需求密度变化的影响较小,约为0.65.由图4(b)可知,由于乘坐DRT的乘客所占比例变化较小,在收益约束的影响下,当需求水平较低时,运营商必须设定较高的DRT票价以保证非负的运营商收益.反之,随着需求密度的增大,当需求水平大于一定值时(如λ≥80 人/(h·km2)),即使运营商收取最低的DRT票价,总票价收入也能覆盖运营成本,从而实现正收入.对乘客而言,随着需求密度的增大,DRT票价降低,总用户成本随之减少.

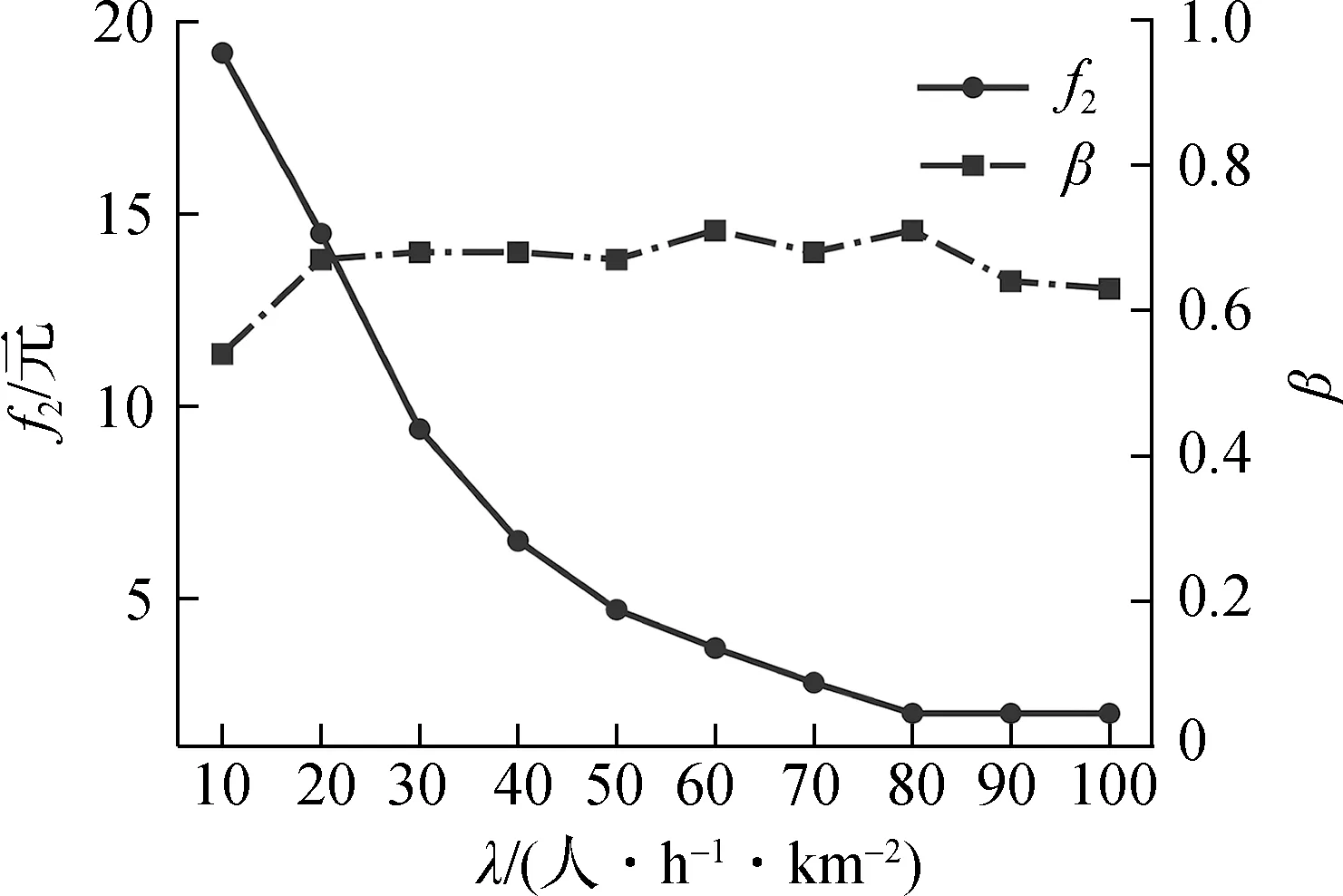
(a) DRT票价和服务区域边界参数

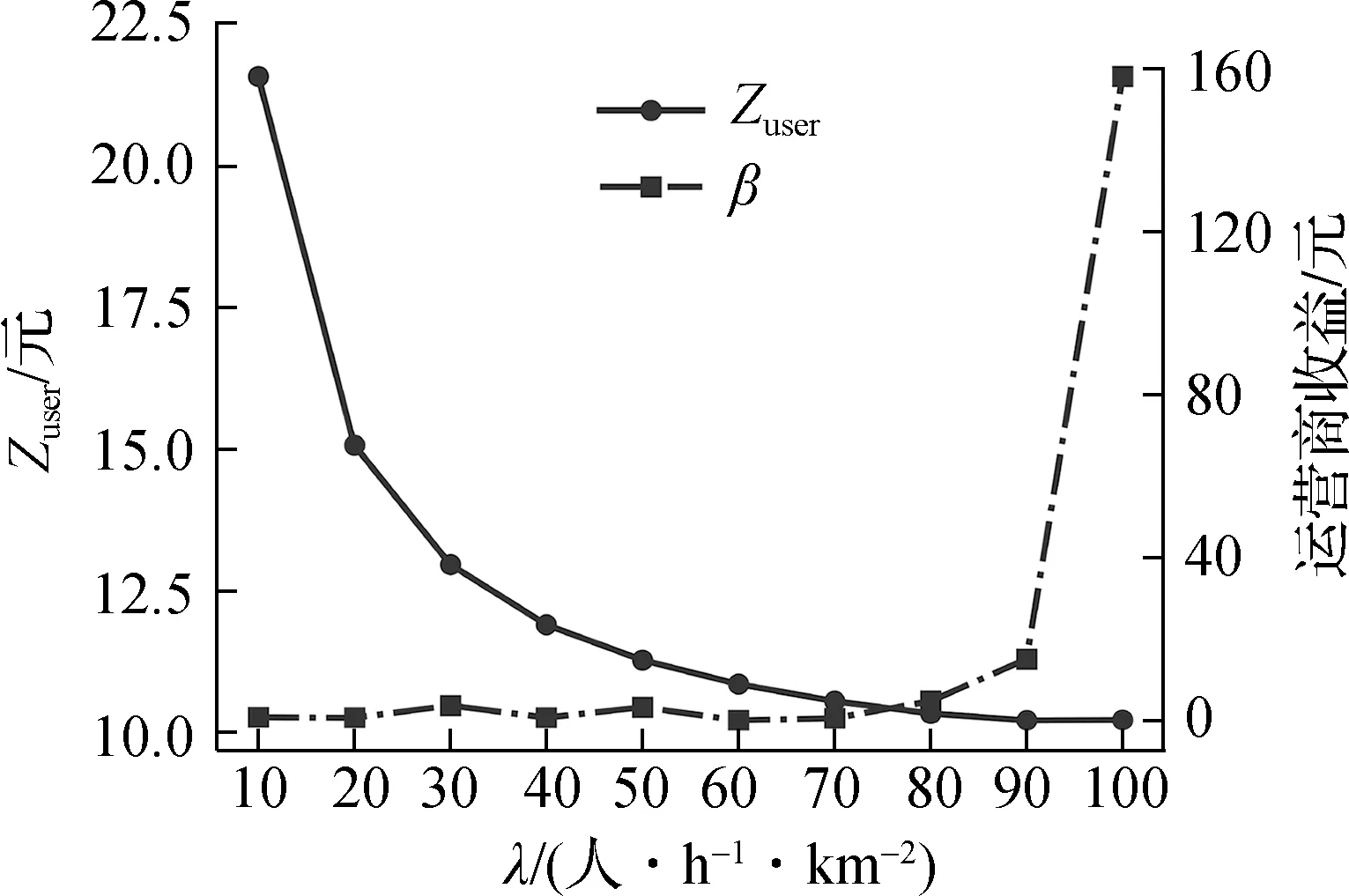
(b) 用户成本和运营商收益

3.3 灵敏度分析

图5给出了不同时间价值下的最优结果对比.由图可知,需求密度较低时,DRT票价随时间价值的增大而减小;需求密度较高时,DRT票价已经降为最低值,不再受时间价值变化的影响.较高的时间价值会降低DAPL-HT中2种公交的服务区域边界参数β.当ctime=20 元/h时,β≈0.65,DRT服务区域面积占总区域面积的24.5%;当ctime=40元/h时,β≈0.60.DRT服务区域面积占总区域面积的比例增加到32.0%,同时类型1和类型2 乘客所占比例也相应增加.用户成本随时间价值的增大而显著增大,这是因为时间价值直接影响了乘客的出行时间成本.

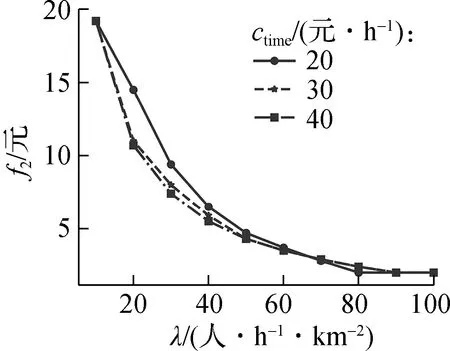
(a) DRT票价

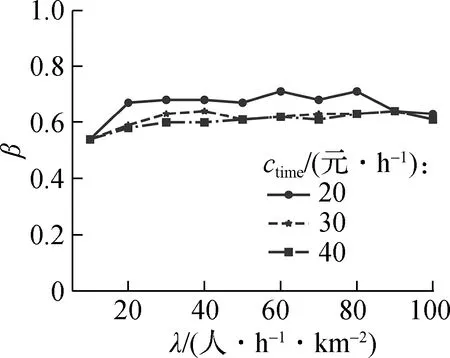
(b) 2种公交服务区域边界参数

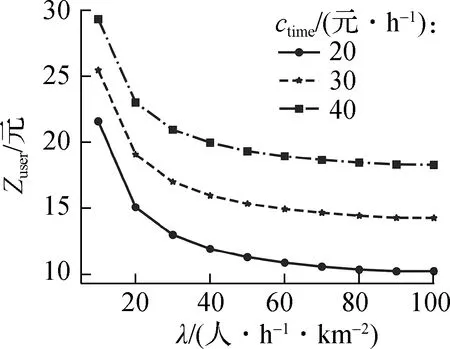
(c) 用户成本

图6给出了不同DRT最大偏移距离s下的最优结果对比.由图可知,在同一需求水平下,随DRT最大偏移距离的增大,DRT票价逐渐减小,而DAPL-HT中2种公交的服务区域边界参数变化较小.当s=0.6,0.9,1.2 km时,相比最低需求水平,最高需求水平下的用户成本分别减少11.36、6.98、4.69元,分别降低52.6%、36.9%、25.3%.由此表明,DRT最大偏移距离越小,用户成本随需求密度增加而下降的速度越快.因此,在较低的需求水平下,可能会存在一个最优的DRT最大偏移距离,使得用户成本最小化.本算例中,当λ=20 人/(h·km2)时,DRT最大偏移距离最优值为0.9 km,其对应最小的用户成本为14.77元,DRT票价为8.2元,DAPL-HT中2种公交的最佳服务区域边界参数β=0.61,DRT、FRT服务区域面积分别占总区域面积的30.4%和69.6%.

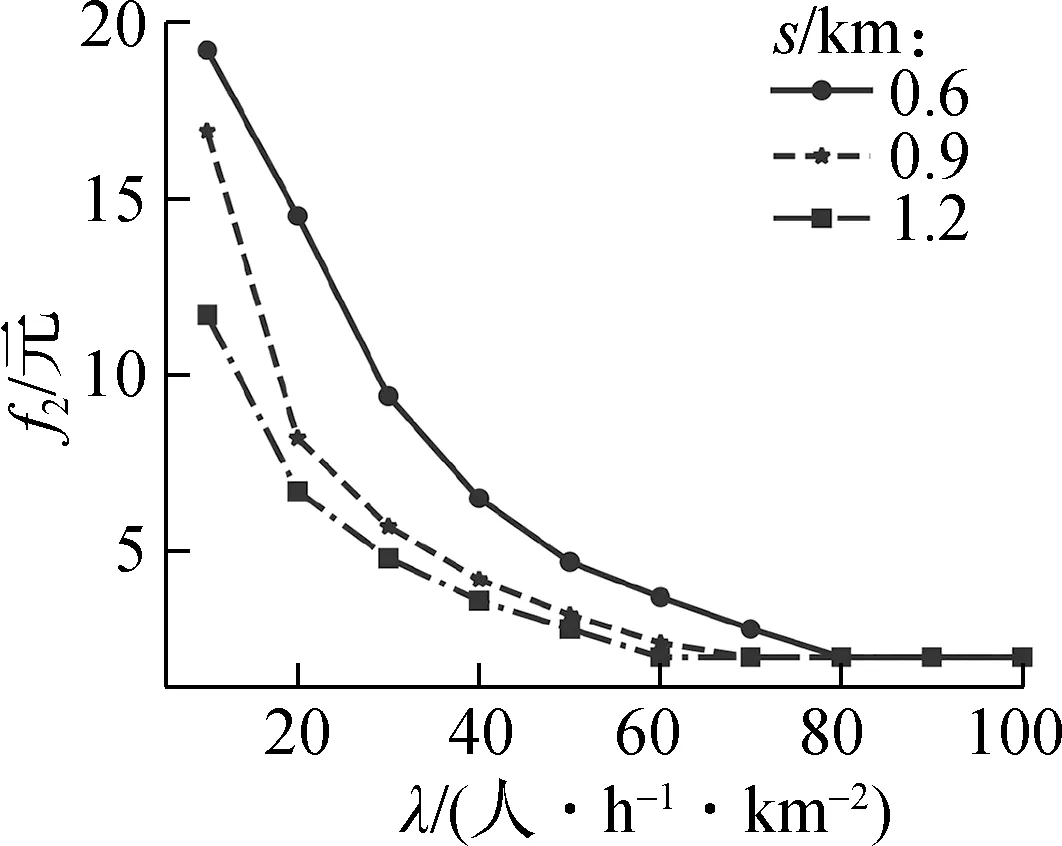
(a) DRT票价

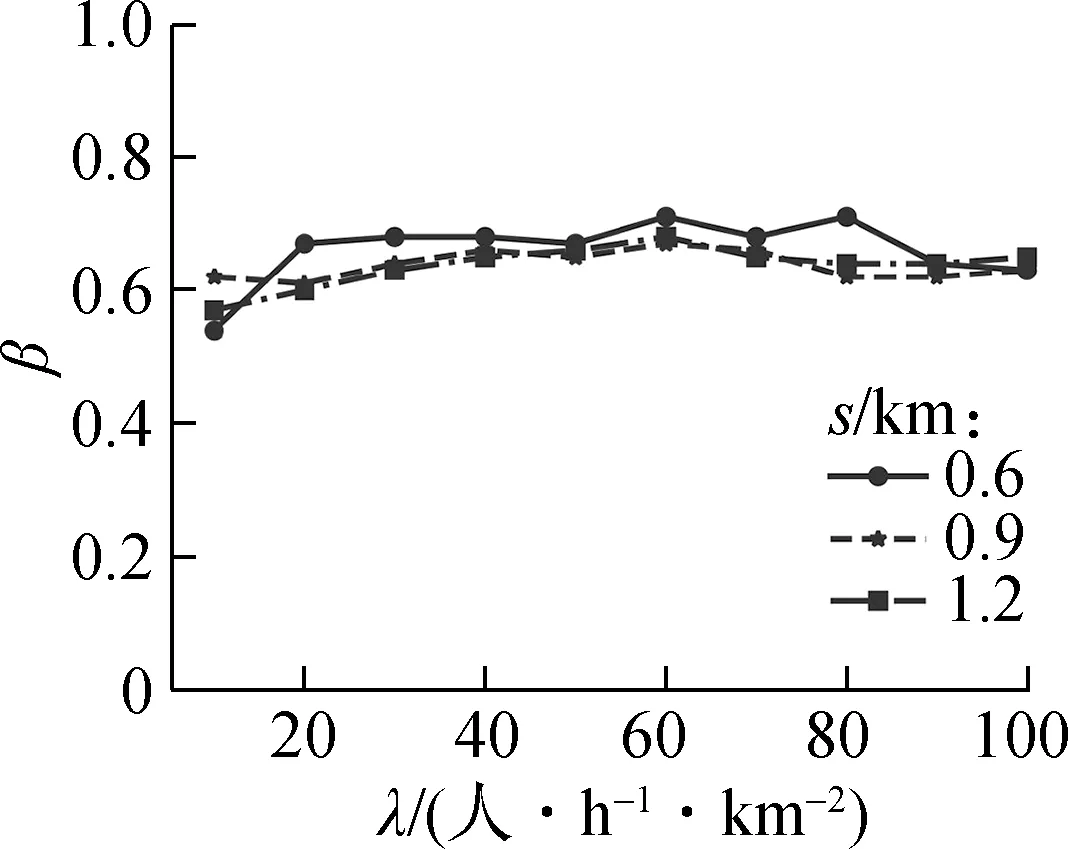
(b) 两类公交服务区域边界参数

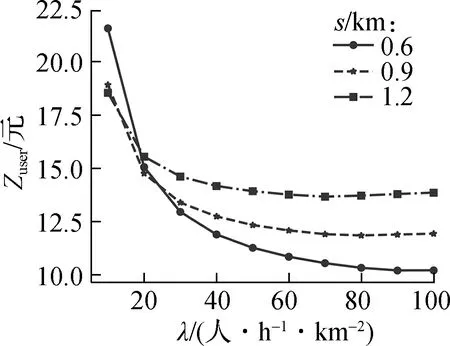
(c) 用户成本

此外,根据图5和图6可知,在不同的时间价值和最大偏移距离测试场景下,DAPL-HT中2种公交的服务区域边界参数β∈(0.54,0.71),均大于0.5;DRT的最佳服务区域面积约占总服务区域面积的16.8%～42.3%,均小于50%.因此,在设计的线性走廊区域中,DRT的最佳服务区域面积均小于FRT.

4 结论

1) 以DAPL-HT系统为研究对象,在设计的线性走廊公交服务区内,以用户成本最小为目标,以运营商收益非负为约束条件,构建了一个非线性优化模型,协同优化DRT票价和系统中FRT/DRT的服务区域面积, 并设计数值实验以分析优化模型的特性.

2) 在不同的需求密度条件下,最优DRT票价值随乘客需求密度的增加而减少, DAPL-HT中FRT和DRT的服务区域边界参数受需求密度变化的影响较小.

3) 灵敏度分析实验表明,时间价值对2种公交的服务区域影响较大,当时间价值从20元/h增大到40元/h时,DRT服务区域面积占总区域面积的比例从24.5%增大到32.0%.在不同的DRT最大偏移距离下,低需求密度时需求响应式公交的最大偏移距离与用户成本成负相关,高需求密度时则相反.此外,在不同的时间价值和最大偏移距离测试场景下,设计线性走廊区域中DRT的最佳服务区域面积约占总区域面积16.8%～42.3%.

4) 建模过程中尚未考虑站间距、出行选择以及换乘惩罚等因素的影响.因此,下一步研究可以考虑引入更多的相关优化设计参数,分析其对混合公交系统中用户成本和运营者收益的影响.