有限维Leavitt路代数的分次双代数结构①

蒋秋晴， 王正攀

西南大学 数学与统计学院，重庆 400715

Leavitt代数是文献[1]给出的不满足基数不变性的一个典型例子, 一般记作LK(1,n), 其中n是正整数, K是一个域． Leavitt路代数是基于有向图定义的满足一定生成关系的一类代数, 是Leavitt代数的自然推广, 由文献[2-3]各自独立引入． Leavitt路代数与Bergman代数、 图C*-代数、 半群等若干类代数有着密切联系, 近些年受到了广泛关注, 有限维Leavitt路代数是一类半单代数[4-8]．

Hopf代数的分类, 是代数学者长期关注的重要问题, 近年来, Hopf代数也在组合研究领域中崭露头角[9]． 有限维半单代数上有丰富的Hopf代数结构[10-11], 相关研究在Hopf代数的分类中举足轻重, 有向图也是研究Hopf代数分类问题的手段之一[12-13]． 有限维Leavitt路代数作为半单代数自然也有Hopf代数结构, 但Leavitt路代数同时具有整数分次结构(Z-分次结构)[14], 其上是否具有Z-分次的Hopf代数结构尚不清楚, 本文给出了有限维Leavitt路代数具有Z-分次双代数结构的充要条件．

(a) 结合性:m(I⊗m)=m(m⊗I);

(b) 单位性:m(I⊗μ)=s2,m(μ⊗I)=s1;

(c) 余结合性: (I⊗Δ)Δ=(Δ⊗I)Δ;

(d) 余单位性:s2(I⊗)Δ=I=s1(⊗I)Δ;

则称B是一个K-双代数, 记μ(1K)=1, 则1是B的单位元[15]． 若B=⨁n∈ZBn是K-双代数, 且满足:

(i)BiBj⊆Bi+j(∀i,j∈Z);

(ii) ΔBn⊆⨁i+j=nBi⊗Bj(∀n,i,j∈Z);

则称B是Z-分次K-双代数．

r′(e)=r(e)r′(e*)=s(e)s′(e)=s(e)s′(e*)=r(e)

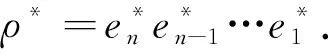
(V)uv=δu,vv(∀u,v∈Γ0);

(E1)s(e)e=er(e)=e(∀e∈Γ1);

(E2)r(e)e*=e*s(e)=e*(∀e∈Γ1);

(CK1)e*e′=δe,e′r(e)(∀e,e′∈Γ1);

称Γ为LK(Γ)的底图． 对∀v∈Γ0,e∈Γ1, 定义

deg(v)=0 deg(e)=1 deg(e*)=-1

则LK(Γ)形成Z-分次K-双代数．

一些简单的底图上的Leavitt路代数同构于我们熟知的若干代数． 例如, 全矩阵代数Mn(K)同构于LK(Γ1), 其中n为正整数,Γ1为有向n-线性图, 即由n个顶点、n-1条首尾相连的边形成的有向图． 又如, 劳伦多项式代数K[x,x-1]同构于LK(Γ2), 其中(Γ2)0={v}, (Γ2)1={e}, 且s(e)=r(e)=v． 再如, Leavitt代数LK(1,n)同构于LK(Γ3), 其中n为大于1的正整数, 且(Γ3)0={v}, (Γ3)1={e1, …,en}, 对∀i=1,…,n, 有s(ei)=r(ei)=v．

另外, 有限维Leavitt路代数含有单位元, 且同构于某一个分块矩阵代数[5,16]．

引理2若Leavitt路代数LK(Γ)是有限维K-代数, 则必存在Γ′是有限个有限线性图的并, 使得LK(Γ)≃LK(Γ′)．

引理3若Γ是有限个有限线性图的并, 则B={ρ,ρ*:ρ∈Path(Γ)}是LK(Γ)的一个K-基．

定理1有限维Leavitt路代数形成Z-分次双代数当且仅当其底图含有孤立点．

证据引理2、 引理3, 假设Γ是有限个有限线性图的并, 且B是由Γ的路径形成的LK(Γ)的K-基．

必要性已知LK(Γ)具有Z-分次双代数结构． 因为是代数同态, 所以

(v)=1

且对∀v∈Γ0, 有(vv)=(v)(v)=(v), 即(v)∈{0, 1}． 故存在唯一的u∈Γ0, 使得对∀v∈Γ0, 有(v)=δuv． 下证u是孤立点, 否则, 必存在e∈Γ1, 使得s(e)=u或r(e)=u． 不妨假设s(e)=u． 注意到u≠r(e), 有(ee*)=(e)(e*)=(u)=1, 即(e)≠0． 另一方面(e)=(er(e))=(e)(r(e))=0, 矛盾． 因此,u为孤立点．

充分性若Γ含孤立点, 令B=B1∪ + B2, 其中B1={v1, …,vt}为Γ的孤立点集． 任取β∈B{vt}, 定义

(vt)=1(β)=0

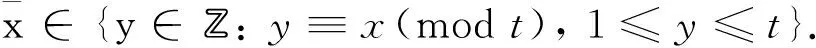
(1)

以下仅需分别验证双代数的定义中的(c),(d),(e)3条．

(d)任取vi∈B1, 有

任取β∈B2, 有

即s1(⊗I)Δ=I=s2(I⊗)Δ．

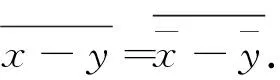
任取β∈B2, 基于(1)式可得

即(Δ⊗I)Δ=(I⊗Δ)Δ．

Δ是代数同态． 任取λ,γ∈B, 若λ,γ∈B1, 则

即Δ(λγ)=Δ(λ)Δ(γ)． 若λ,γ∈B2, 当λγ=0时, 显然Δ(λγ)=0=Δ(λ)Δ(γ); 当λγ≠0时, 则存在κ∈B2使得κ=λγ, 且

即Δ(λγ)=Δ(κ)=Δ(λ)Δ(γ)． 当λ,γ不同时在B1或B2时, 显然Δ(λγ)=0=Δ(λ)Δ(γ)． 总之, 对∀λ,γ∈B, Δ(λγ)=Δ(λ)Δ(γ)．

综上所述, (LK(Γ),m,μ, Δ,)可形成Z-分次双代数．