基于阿基米德Copula的极尾相依Copula的渐近展开①

廖娟， 彭作祥

西南大学 数学与统计学院，重庆 400715

连接函数Copula[1]可以将多个边缘分布函数结合成一个联合分布函数, 其中边缘分布是随机变量的分布, 因此可以借助连接函数来刻画变量之间的相依关系． 关于Copula函数的性质及其应用的更多研究, 见文献[2-4]．

Copula函数族中有种类众多的Copula函数, 包括阿基米德Copula、 椭圆Copula、 极值Copula等． 阿基米德Copula是一种性质优良的Copula函数, 具有构造简单、 计算容易且便于应用的优点．

(1)

则称Copula

C(x,y): =ψ[-1](ψ(x)+ψ(y))

(2)

为阿基米德Copula且函数ψ是C的生成元． 当ψ(0)=∞时, 则称生成元ψ和其对应的阿基米德Copula是严格的[5]．

(3)

利用Copula可以解决许多重要问题, 其中就有极值问题． 极值理论需要估计比以往所观测到的现象更极端的事件的发生概率, 因此引发了对条件随机向量相依结构的研究． 文献[7]提出了CopulaC在水平u的极尾相依Copula的概念．

对于一个CopulaC并且u∈(0, 1)使得C(u,u)>0, 令

(4)

关于C在水平u的极尾相依Copula为

(5)

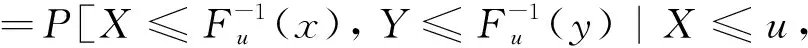
文献[10-13]讨论了正规变换函数和二阶正规变换函数, 用以研究某个估计量的收敛速度, 本文讨论生成元ψ在原点处满足二阶正规变换的条件下, 即ψ∈2RV-α,β(0+), 其中

(6)

辅助函数A(t)是定号的(见文献[14]), 得到极尾相依CopulaCu的渐近展开．

1 渐近展开式

Cu(x,y)=CCl,α(x,y)(1+o(A∘ψ-1(2ψ(u))))(1+B(u)(1+o(1)))

(7)

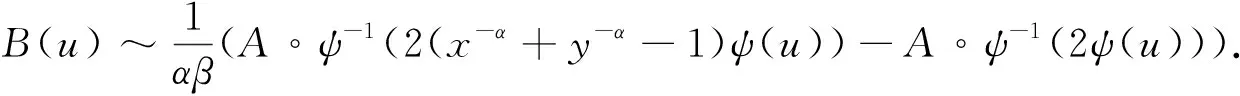
证对于生成元为ψ的阿基米德CopulaC, 由文献[7]命题3.2知

(8)

且根据(2),(5)和(8)式, 有

令k=ψ-1(2ψ(u)), 那么

(9)

由ψ∈2RV-α,β(0+), 0<α<∞,β>0, 辅助函数为A(t)可得

(10)

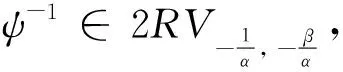
(11)

(12)

(13)

其中, 令

则有

Cu(x,y)=CCl,α(x,y)(1+o(A∘ψ-1(2ψ(u))))(1+B(u)(1+o(1)))

定理证毕．

2 实例

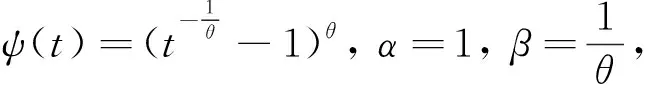
(14)

将ψ和ψ-1的具体表达式代入(14)式, 令

则有

并且

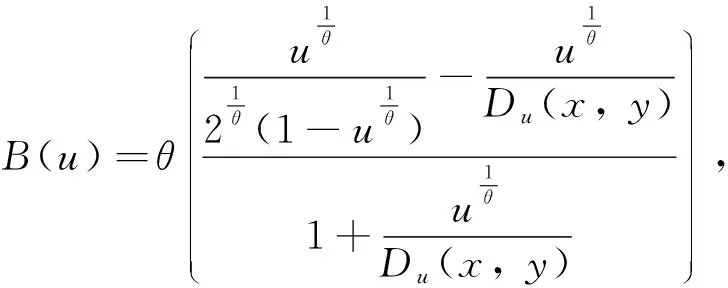
且

Cu(x,y)=CCl,α(1+o(A∘ψ-1(2ψ(u))))(1+B(u)(1+o(1)))

与定理的结论一致．

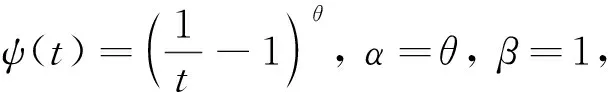
(15)

令

将ψ和ψ-1的具体表达式代入(15)式得

并且,

令

且

Cu(x,y)=CCl,α(1+o(A∘ψ-1(2ψ(u))))(1+B(u)(1+o(1)))

与定理的结论一致．