自适应主动避障管道机器人结构设计及运动分析①

还梦媛， 朱子辰， 曾宪勇

1.重庆机电职业技术大学 工商管理学院，重庆 402760；2.重庆大学 机械与运载工程学院，重庆 400044；3.重庆机电职业技术大学 机械工程学院，重庆 402760

管道运输系统使用机器人进行检测已有数十年的历史, 而在诸多的管道检测作业中, 市政下水管道系统的检测工作是城市污排水处理的重要保障． 目前我国的市政管道检测已尝试使用管道机器人下管检测, 并形成了相关行业规范[1]． 我国的市政排水管道系统大多为铺设长度数十米的水平直管, 直径范围为200 mm到1 m以上[1-2]． 管道材质可能为铸铁、 混凝土、 PE管等． 管道系统一般无弯道, 直管相接处设置方形窨井连接． 管道内部工况复杂, 可能存在管道破裂、 变形、 腐蚀、 起伏脱节等结构性缺陷, 以及沉积、 结垢、 障碍物、 树根等功能性缺陷[1]． 另外, 我国各地的市政下水管道系统建成时间不一, 采用形制不同, 管道直径规格不同． 这给下管检测工作和检测设备设计造成了困难．

尽管适应不同类型管道的机器人种类繁多, 但出于市政管道本身工况, 目前国内外成熟的市政污排水管道检测机器人设计多以四轮小车或履带轮压壁式机器人为载体[3-9], 其上搭载检修设备． 四轮检测小车在管道底部行进, 难以通过淤泥沉积的管道, 也不能避开底部的石块和树根; 对于管壁上阻碍压壁通行的障碍物, 履带轮式机器人缺乏改变压壁位置, 在管道中主动避障的能力． 在适用于其他类型管道检测的机器人中, 存在管内位姿调整较灵活的轮履带式机器人设计[10-17], 近年来越避障性能独特的磁吸式、 多足式和流体机器人设计也层出不穷[18-20], 但这些设计的机构运动原理并不能完全适应市政管道的越避障工况和驱动性能需求．

本研究基于现有管道机器人存在的不足, 设计一种具有管内主动变径和避障功能的机器人结构, 对机器人在管内运行情况进行分类分析, 并提出机器人在管道行驶的越避障运动方案． 所设计机器人的运动模块能沿管周偏转, 快速实现管内位姿偏转和运动模式变换, 满足市政管道检测的越避障需求．

1 机器人结构原理和机构设计

1.1 主要机构设计

如图1所示, 所设计的机器人采用双驱动轮双转向轮设计． 主体结构分为3个部分: 中心模块和两侧的运动模块． 中心模块布置有正反牙对称滚珠丝杠、 两个花键滑轨、 丝杠电机和模块偏转电机及其传动机构; 运动模块装备有一个转向轮和一个驱动轮, 以及转向伺服电机和驱动电机; 中心模块和两个运动模块间由变径机构剪叉臂连接． 管道机器人各机构主要尺寸见表1．

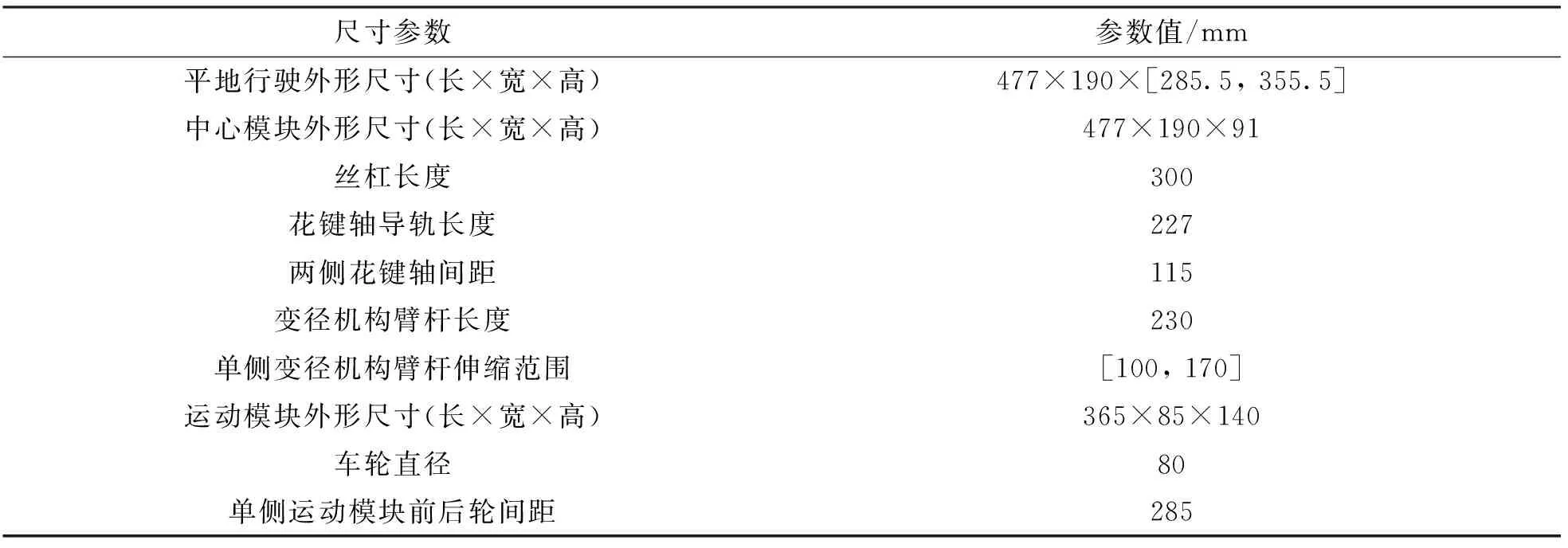
表1 管道机器人主要机构尺寸参数表

图1 管道机器人模型

所设计的机器人能够在圆形管道内一定高度处实现压壁行走, 能够通过运动模块的偏转经方形联通窨井进入圆形管道, 结合转向轮实现沿管道周向旋转, 从而实现避障功能．

1.2 变径机构

现有管道机器人常用的变径机构主要有3类: 蜗轮蜗杆、 升降机式和滚珠丝杠螺母副[20]． 本研究设计双剪叉臂和滚珠丝杠螺母副以实现机器人越障及管道适应性, 具备结构紧凑、 力学性能好的特点．

在中心模块上布置丝杠驱动电机, 在花键轴和运动模块上分别布置滑动和固定铰接座(图2), 使各变径臂铰接成剪叉结构, 通过丝杠电机作用, 驱动丝杠螺母和滑块直线移动, 改变机器人支腿长度, 从而适应不同管径．

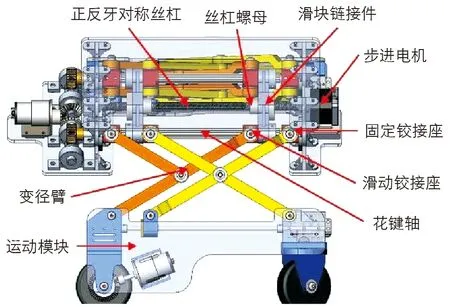
图2 管道机器人变径机构模型

1.3 模块偏转机构

现有的运动模块偏转设计多使用连杆和齿轮传动[4,9], 而这些设计中不含主动变径机构． 本研究设计的偏转机构结合剪叉式变径机构, 考虑中心模块上滑块直线移动需要, 使用花键轴同时提供导轨和传递力矩, 再结合空间尺寸布置传动链, 将变径机构和偏转机构有效地结合起来, 实现机器人紧凑结构设计．

如图3所示, 在机器人中心模块上布置直流减速电机, 经锥齿轮、 蜗轮蜗杆传动, 向两侧的花键轴传递力矩, 此时花键轴作为偏转力矩传动件使用, 变径臂和运动模块随花键轴旋转, 直至运动模块偏转至指定角度, 运动模块偏转后不同位姿见图4．

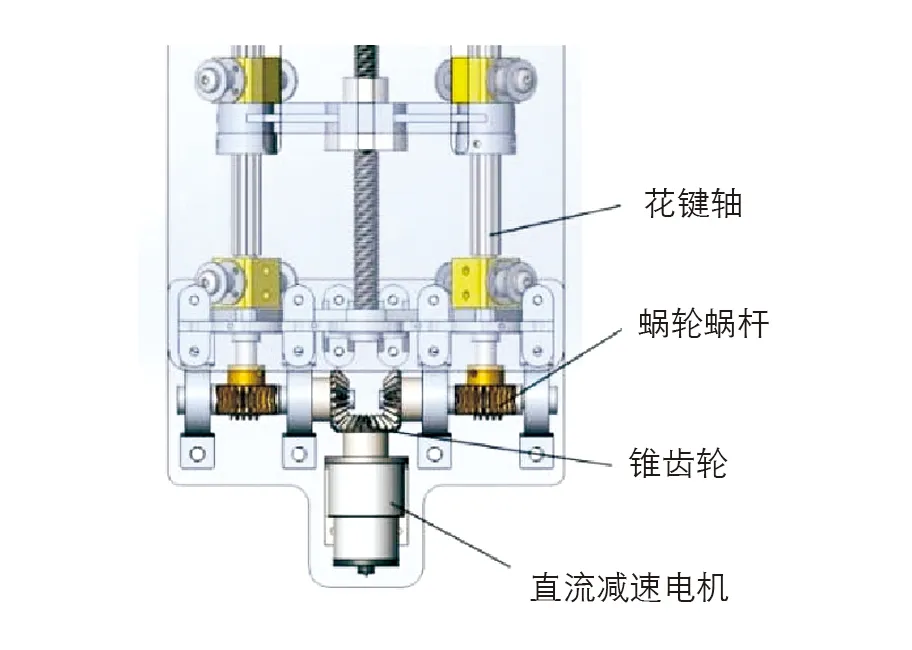
图3 管道机器人模块偏转机构模型

图4 运动模块偏转后不同位姿示意

1.4 运动模块

如图5所示, 运动模块由一个转向轮和一个驱动轮构成, 舵机布置在前轮上方控制车轮转向, 直流减速电机经锥齿轮传动驱动后轮． 前后轮架由两根光轴固定连接, 光轴同时作为变径机构滑轨滑移． 当转向轮偏转一定角度, 运动模块便会在机器人整体前进的同时相对于管壁作转向运动, 两模块运动的组合可使机器人完成越避障变换．

图5 管道机器人运动模块模型

2 机器人管径适应性分析

2.1 变径机构几何参数计算

图6为机器人剪叉式变径机构简图． 以B点为原点, 设BA方向为x轴正方向,BD方向为y轴正方向． 其中,A和A′点为花键轴滑块铰接点,B和B′点为花键轴固定铰接点,C点为运动模块滑块铰接点,D和D′点为运动模块固定铰接点,E点为两臂铰接点;α为AD臂与花键轴夹角;L0为单臂长度．

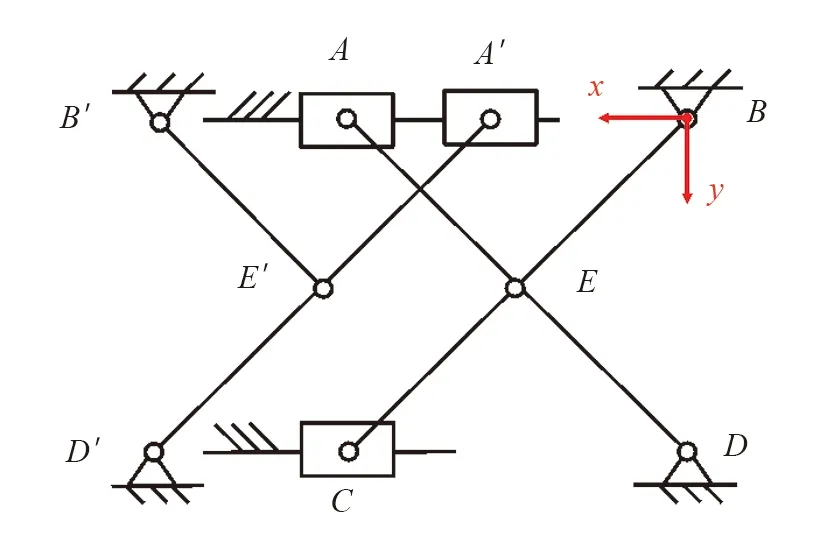
图6 剪叉式变径机构分析

机器人机构对称, 单独研究AD臂, 机构几何参数关系式为:

(1)

其中:yD为单侧变径长度值, 不同夹角α下xA的差值为滑块移动距离．

此次设计采用的具体数据为:L0=230 mm, 花键滑轨总长度为227 mm． 为避免内部构件干涉, 单侧机构实际变径范围为Ls=[100, 170] mm, 变径长度与运动模块总长La范围为[240, 310] mm, 变径臂与花键轴夹角α范围为[26.25°, 47.63°]．

2.2 管径适应性分析

所设计机器人可适应的管径范围为450 mm以上． 对于直径612 mm以上的管道(图7a为650 mm管道, 图7b为1 000 mm管道), 机器人运动模块沿管道径向压壁, 越过底部淤泥和障碍物, 此时机器人的运动性能和稳定性较好． 变径机构长度改变, 所设定的运动模块偏转角的值随管径增大而减小, 以扩大管径适应的最大范围．

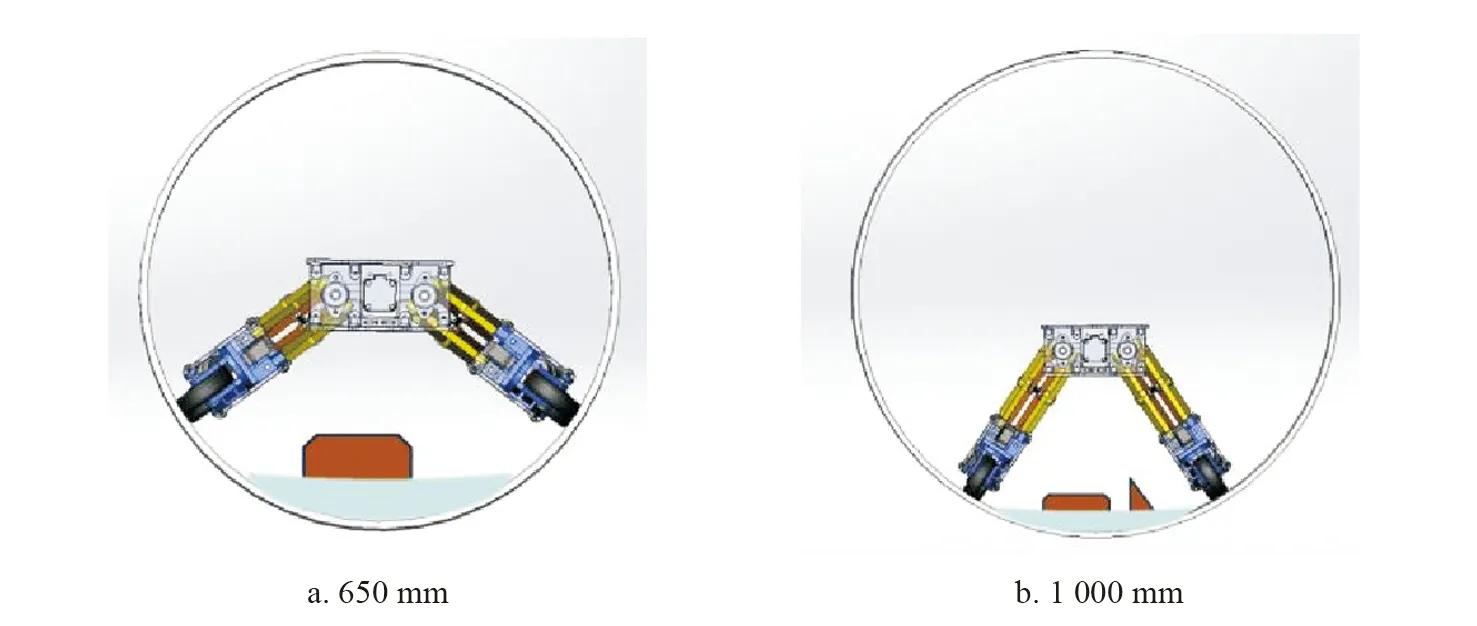
图7 在直径612 mm以上的管道内机器人行进示意

对于450～612 mm直径管道(图8a为450 mm管道, 图8b为600 mm管道), 机器人摆臂偏转角度较小． 变径机构长度固定, 所设定的运动模块偏转角随管径减小而减小． 在这一变径范围内, 同一管径的运动模块偏转角的值存在多解．

图8 在450～612 mm管道内机器人行进示意

对于这两种不同的管径范围, 视运动模块垂直为默认姿态, 简化机器人在管道横截面上的结构, 可做出管径适应性几何分析图(图9)． 其中点O为管道中心;Lp为两花键轴间距, 设计参数为115 mm;La为变径长度和运动模块总长度, 其最小值Lamin为240 mm;R为管道半径, 运动模块偏转角φ为运动模块所在平面与机器人对称平面夹角．

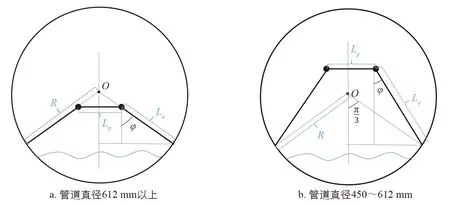
图9 管道内机器人管径适应性分析

考虑使管径适应范围尽可能大, 同时使机器人行进稳定, 由图9几何分析可知, 运动模块偏转角φ分别满足几何数值关系:

(2)

由(2)式可得, 管径450～612 mm范围内模块偏转角φ范围为从35°到60°递增; 管径612～850 mm范围内模块偏转角φ范围为从60°到30°递减, 两侧运动模块夹角为偏转角的两倍, 其范围为从120°到60°递减．

3 管道机器人运动分析

3.1 管内压壁行驶运动简化模型

本研究所设计的管道机器人可避开管道障碍物, 以一定姿态角利用运动模块着力于管道侧面压壁行驶． 在管道横截面上将机器人简化为如图10和图11所示的三杆系统, 进行运动位姿分析, 将机器人部件视为刚体, 同时忽略车轮厚度．

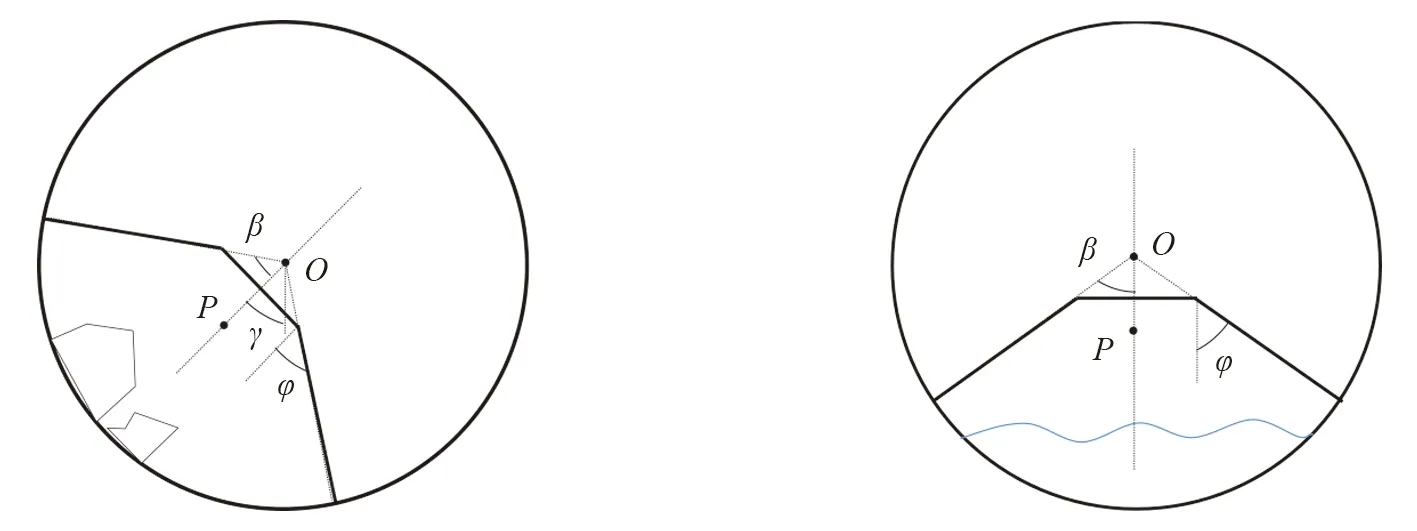
图10 在直径612 mm以上的管道内机器人行驶位姿

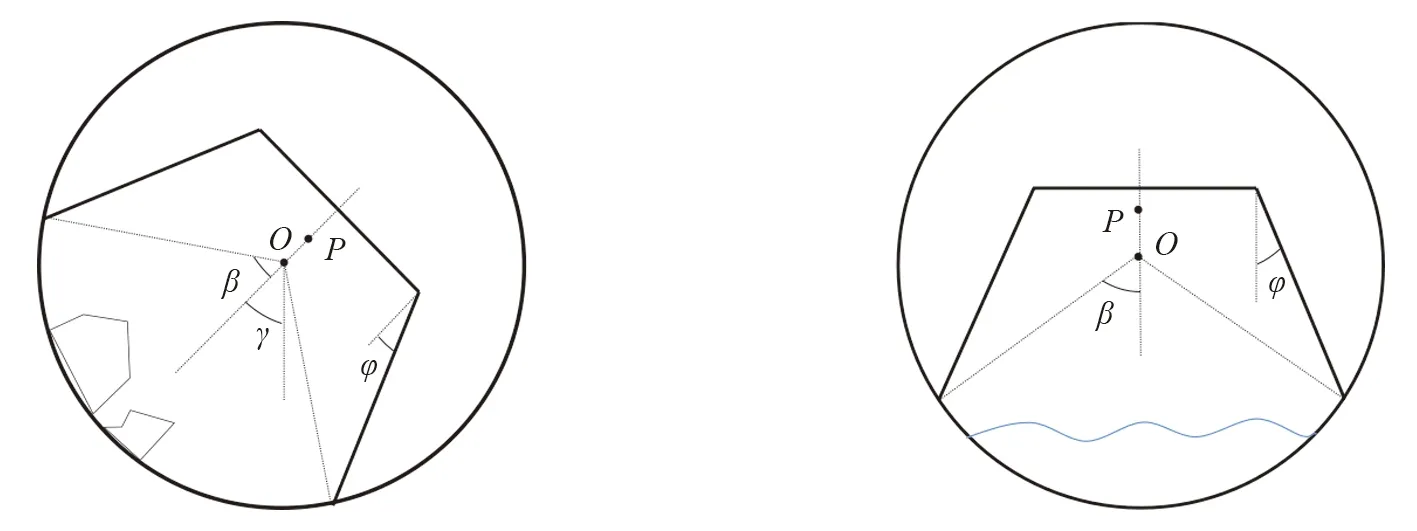
图11 在450～612 mm管道内机器人行驶位姿

在机器人所能运行的管径范围内, 可根据行驶时的压壁情况分为两类．

1) 在直径612 mm以上的管道中, 机器人可做到车轮正对管道内壁行驶, 此时管道中心O在运动模块中心P之上(图10)．

2) 在450～612 mm直径管道中, 此时管道半径中心在运动模块中心之下(图11)．

在图10和图11中, 以水平和竖直方向分别作为x和y轴方向,O点为管道横截面圆心,P点为机器人机身模块重心(考虑到机器人为对称结构, 其机身模块重心必定在机器人的对称平面上);hp为O,P两点连线距离;γ角为O,P连线与竖直平面夹角, 称为姿态角;φ角为运动模块所在平面与O,P连线(即机器人对称平面)夹角, 称为模块偏转角;β为压壁点与管道横截面圆心连线夹角的1/2, 称为张角(直径为612～850 mm的管道中,β=φ; 直径为450～612 mm的管道中,β设为60°)．

3.2 越避障运动方案

为适应市政管道检测工况, 机器人具有几种运动模式: 用于适应窨井行驶的平地行驶, 管内压壁正常行驶, 从窨井底部平地行驶转变为管内行驶的管外—管内越障变换, 通过周向旋转躲避障碍物的管内避障变换． 本研究将具体分析机器人通过转向轮和模块偏转机构进行管内主动越避障运动的运动变换方案．

将管道内表面转化为如图12所示的展开平面[10],x轴方向沿管道中轴线,y轴方向沿展开的管道圆周线． 为简化分析, 将运动模块与管道半径视为处于同一平面上, 此时运动模块垂直于展开平面, 如此可将机器人车轮在管道内表面上的运动转化为在展开平面上的平面运动．

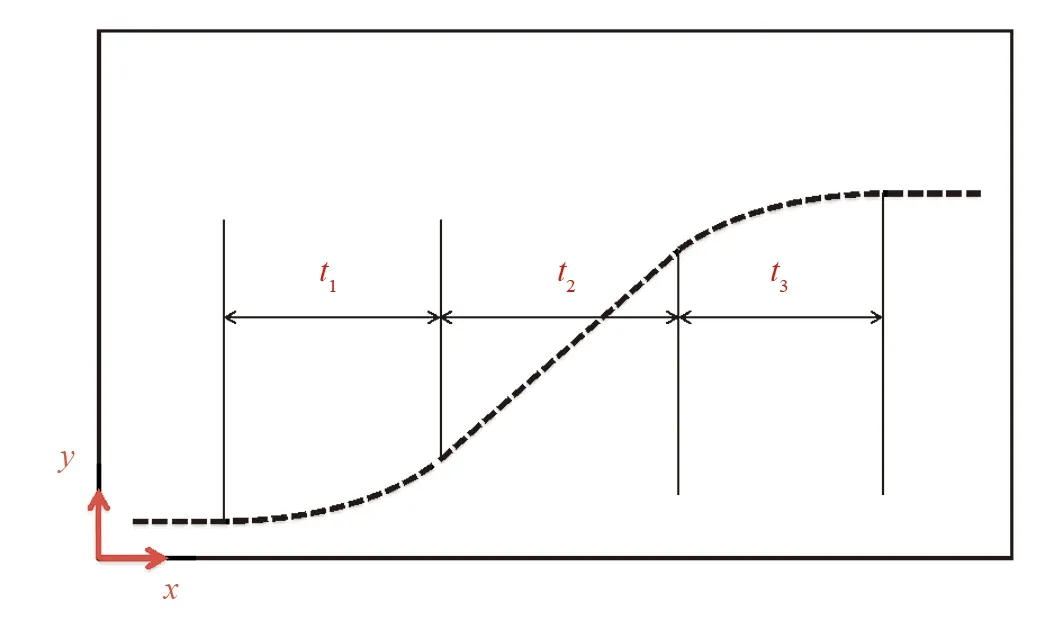
图12 管道内表面展开平面和运动模块行进路线示意

将单一运动模块视为具有一个驱动轮和一个转向轮的运动系统, 其在展开平面上的运动可视为平面上的转向运动(图13)． 其中,WA点为前轮中心,WB点为后轮中心,WC点为前后轮接触点连线中点在展开平面上的投影,OW点为转向运动圆心,Lf为WAWB距离,Lb为WBWC距离,V为WC点速度,δf为前轮转角,δm为质心速度与后轮所指方向夹角,δc为后轮所指方向与x轴夹角,Rz为转向运动半径． 其中Lf和Lb等几何参数为已知量, 运动参数设定值有2个: 转向轮转向角度δf, 驱动轮转速Vb=Vsinδm．

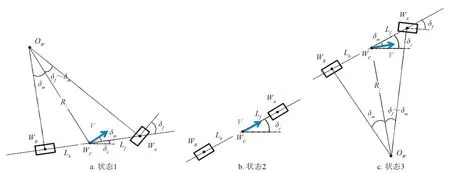
图13 运动模块的几种运动状态分析

δm可由三角函数求得:

(3)

转向运动半径Rz可由三角函数求得:

(4)

则系统转向角速度, 即后轮所指方向与x轴夹角δc变化率ωδc可表示为

(5)

运动模块沿x轴方向速度Vx、 沿y轴方向速度Vy为:

(6)

机器人越避障运动参数设计需要考虑车轮与管壁的摩擦力和机器人位姿倾斜重心, 以避免机器人避障时产生滑移或倾覆． 因此在进行运动时使用如下策略: 首先, 使转向轮向上偏转一定角度δf, 经过时间t1使运动模块转向角度达到一个较小角度δc1; 之后, 使δf变为0, 使机器人向斜上方前进时间t2; 最终使转向轮向下偏转一定角度δf, 相对于运动模块平面进行第1段运动的镜像运动, 使机器人位姿调平, 完成运动变换, 车轮接触点路径如图12虚线所示．

忽略可能存在的滑移, 可得第1段和第3段运动时间为:

(7)

代入前文公式, 可得到总运动距离LV和LH．

(8)

在y轴方向总运动距离LV已知的情况下, 可解得第2段运动时间为:

(9)

由(8)式求解机器人在进行越障变换时水平方向总运动距离LH． 对于机器人在管道中所进行的不同运动变换, 其y轴方向总路程是不同的．

3.2.1 管外—管内越障变换

机器人在进入管道前, 以小车方式在窨井底部平地中前进, 在进入圆形管道后, 依靠转向轮结构变换运动模式． 管道机器人在前进的同时, 两侧运动模块张开一定角度, 变换为压侧壁行进, 实现对管道底部杂质的越障(图14)．

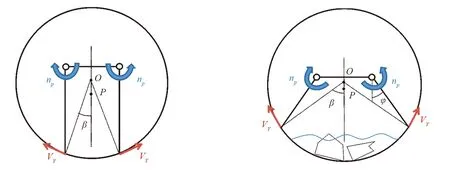
图14 越障变换运动位姿

图15为机器人以本节所述方案在管道中进行越障变换示意图, 可注意到机器人的位姿变化与转向轮角度变化． 图16为按所述机器人结构所搭建的实物样机在500 mm PE圆筒管道内进行越障变换的位姿演示, 运动过程中车轮偏向异侧． 该样机可作为位姿演示和机器人运动机构的验证, 具体运动数据有待进一步测试研究．

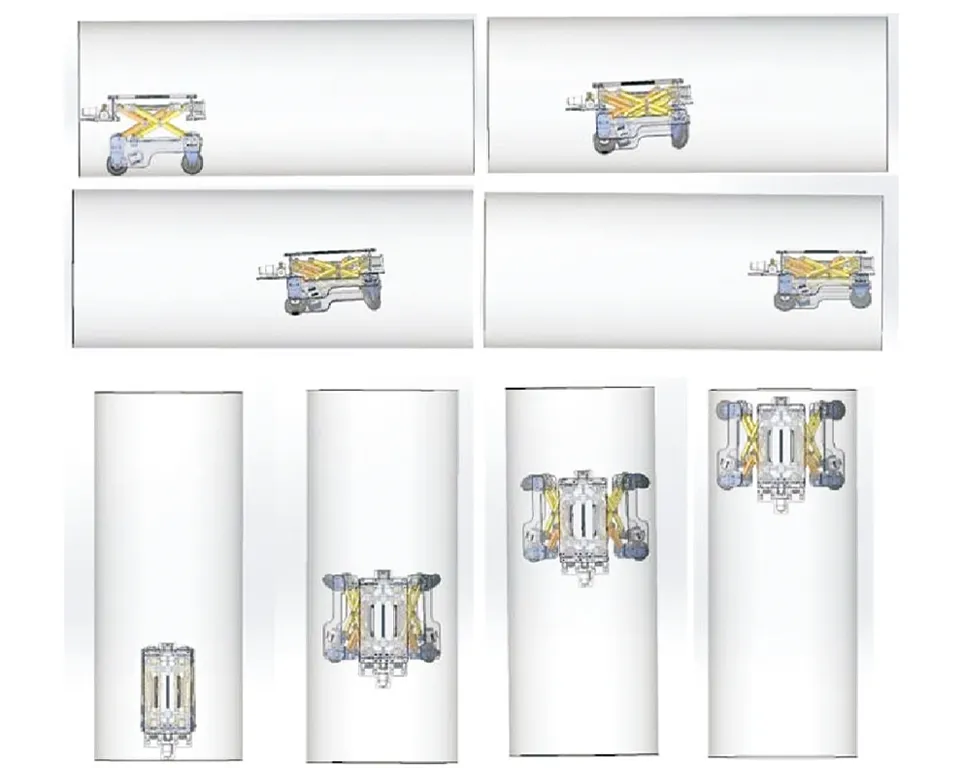
图15 管道机器人越障变换示意

图16 机器人样机500 mm管道内越障变换位姿

在越障运动中, 机器人机身模块重心与管道半径重心不在同一平面上, 这会使转向轮实际转角δ′f与公式中的转角δf存在一定差值, 该差值与管道半径和沿管周行进路程有关, 并且受车轮与管道接触情况影响． 在转角δf设定值较小的情况下, 忽略这一差值影响, 认为δ′f与δf相等．

进行越障变换时,y轴方向总路程已知, 在450～612 mm直径管道中为:

(10)

在612～850 mm直径管道中为:

(11)

其中,β0为各管径下张角β的初始值, 设为:

(12)

3.2.2 管内避障变换

机器人在管道中正常运行时, 姿态角γ为0向前运行, 当管壁出现障碍物或破损、 孔洞等管道缺陷, 依靠两转向轮向同一方向偏转, 实现机器人姿态角的偏转, 以周向旋转的方式改变前进路线, 避开障碍物(图17)．

图17 避障变换运动位姿

避障变换运动过程只需要转向轮角度变化, 不需要运动模块绕花键轴作相对偏转． 运动分析与越障变换相似, 公式通用． 区别在于, 进行避障变换时, 机器人沿管道周向总路程与所设定的姿态偏转角γ有关, 用

(13)

代替(10)和(11)式．

图18为机器人在管道中避障后以一定偏转位姿前进示意图． 图19为实物样机在500 mm PE圆筒管道内进行避障变换的位姿演示, 运动过程中车轮偏向同侧．

图18 管道机器人避障运动示意

图19 机器人样机500 mm管道内避障变换初始位姿

3.3 越避障运动参数计算分析

3.3.1 越避障运动参数随管径变化曲线

给定机器人越避障尺寸和运动参数见表2, 利用前述理论公式计算, 在MATLAB中分别绘制越障运动和避障运动总运动时间、 水平方向总运动距离随管径变化曲线(图20-图21)．

表2 越避障运动参数设定值表

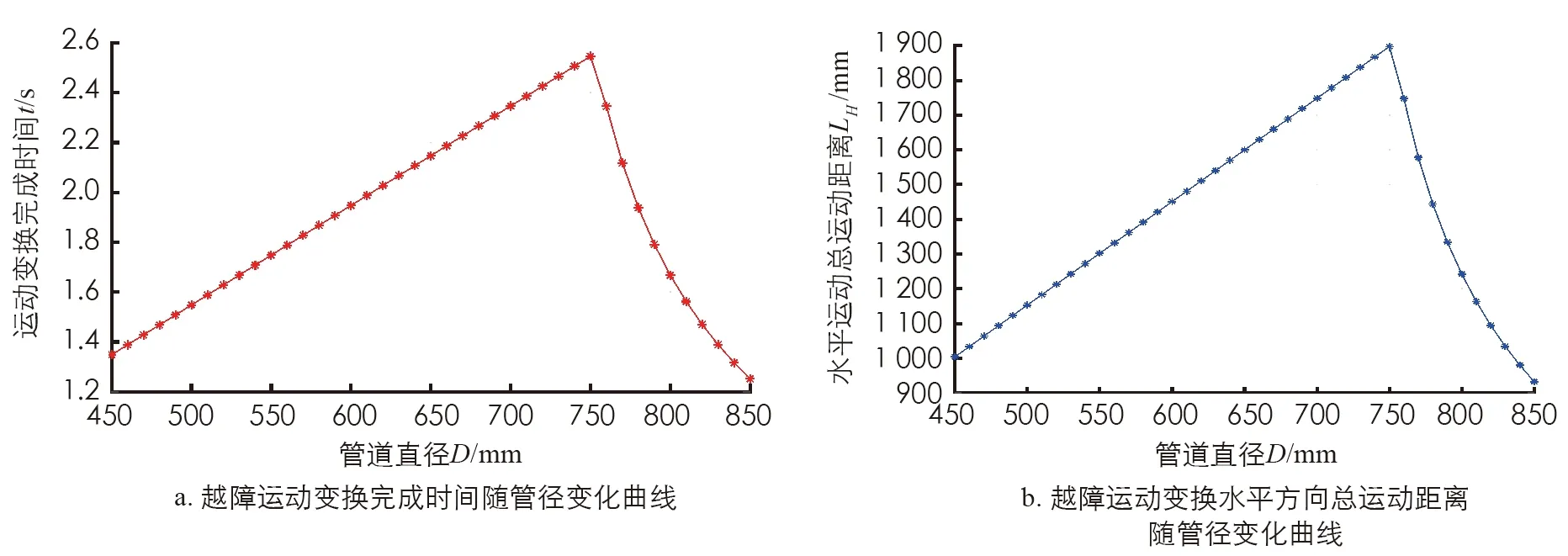
图20 越障运动完成时间和水平方向总运动距离随管径变化曲线

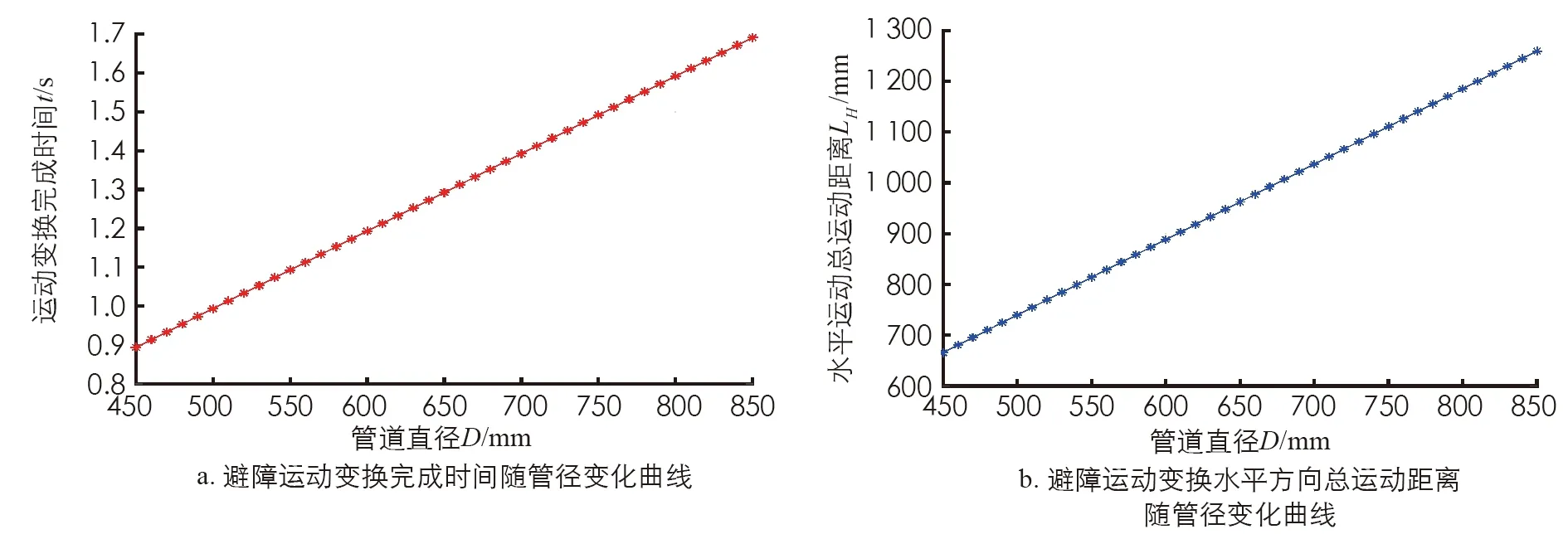
图21 避障运动完成时间和水平方向总运动距离随管径变化曲线

由于对于不同管径采用同一转向轮转角, 影响运动时间和水平运动距离的主要是前文运动方案的第2阶段． 其中, 管径小于750 mm的越障运动完成时间和水平运动距离随管径递增, 管径大于750 mm的越障运动受周向行进路程下降影响, 运动完成时间和水平运动距离随管径递减; 避障运动完成时间和水平运动距离随管径递增．

在给定尺寸和运动参数值的条件下, 机器人在450～850 mm管道中进行越障运动时间理论值在1.2～2.6 s之间, 水平运动总距离理论值在0.9～1.9 m之间; 机器人在管道中进行避障运动时间理论值在0.9～1.7 s之间, 水平运动总距离理论值在0.65～1.3 m之间． 理论值基本符合预期, 在实际应用中, 可根据障碍物和管壁情况, 适当调整转向轮转角, 以改变运行时间和水平运动距离, 或调整驱动轮速度改变运行时间．

3.3.2 越障运动模块偏转电机转速曲线

在越障运动中, 运动模块偏转角φ会随机器人位姿发生变化, 驱动模块偏转机构的电机转速需要适配偏转角转速变化, 以避免驱动轮电机和模块偏转电机提供的驱动力冲突, 故需计算分析模块偏转电机转速随时间变化曲线．

运动模块偏转速度, 即花键轴转速可对模块偏转角φ求导得到． 机器人车轮沿半径R管道周向行驶L′v距离时, 模块偏转角φ为:

(14)

花键轴转速np为:

(15)

模块偏转电机转速nmp为:

(16)

其中:ib为锥齿轮传动比,zb1为主动轮齿数,zb2为从动轮齿数,iw为蜗轮蜗杆传动比,zw1为蜗杆头数,zw2为蜗轮齿数． 本设计中, 取ib=1,iw=1/25．

利用前文公式计算, 绘制越障运动模块偏转电机转速随时间变化曲线(图22), 管道直径D设为750 mm, 其余设定参数值同表2． 曲线图中出现的速度突变由转向轮转角突变造成, 在实际的模块偏转运动中, 可设置转向轮转角连续改变, 以减轻转速突变给电机造成的负担． 同时, 可通过调整驱动轮速度改变运行时间, 以适配模块偏转电机转速调节范围和反应速度．

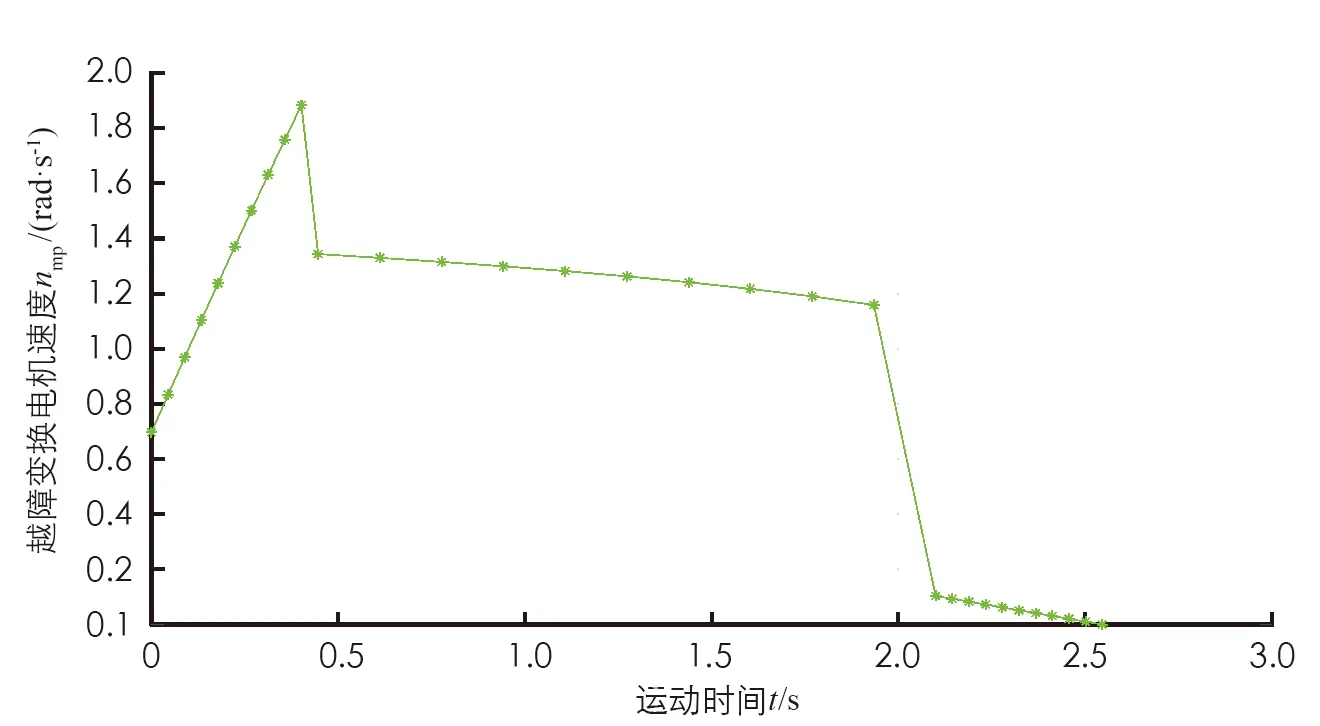
图22 越障运动模块偏转电机转速随时间变化曲线

4 结论

为适应我国城市污水管道检测需求, 本研究设计了一种具有管内主动变径和避障功能的轮式管道机器人, 分析了机器人运动模块的详细设计方案, 阐明了变径机构和模块偏转机构运动机理和传动布置． 针对越障避障的运动适应功能要求, 本研究提出了一种基于模块偏转机构和运动模块转向轮的越避障运动控制方案, 建立了相关运动参数的计算模型, 并计算求解了越障避障运动总运动时间、 水平方向总运动距离随管径变化曲线, 以及越障运动模块偏转电机转速随时间变化曲线． 分析结果表明, 所设计的机器人单侧剪叉机构变长度范围为100～170 mm, 所设计的机器人可在450 mm以上管道中进行灵活越障及避障, 能够较好地满足市政管道爬管越障需求． 近年来, 管道检测的智能方法[22]和有关管道机器人驱动元件的研究[23]也层出不穷, 通过结合这些方法, 管道机器人必将在未来管道检测中持续大放异彩．