基于惯性导航的管道探测蛇形机器人定位算法

王晓铮,王亚慧,张成林

(1.北京建筑大学,机器人仿生与功能研究北京市重点实验室,北京 100044;2.北京建筑大学电气与信息工程学院,北京 102616)

0 引言

管道作为燃气运输的主要方式,具有安全性高、运输方便等优点。然而随着全球燃气规模不断扩大,地下管线日益增多,异常复杂,难以进行日常巡检和维护,特别是管道内部的探测[1]。为了预防管道事故,天津大学开发了一种高精度数据采集和监控系统,目前已应用于管线泄漏检查[2];邓蕊等[3]、邢利辉等[4]设计了一种管道探测蛇形机器人,将检测到的管道内部环境信息上传至上位机,以便工作人员确定是否进行管道维护或开挖。因此对于管道内机器人的定位是至关重要的。

目前应用于管道无损检测中的定位技术有探地雷达法、电磁法和磁强计法等,然而这些方法的定位精度往往会受到外部环境影响。基于惯性器件的定位导航技术是一种完全自主式定位,具有短时间内定位精度高且不受环境影响的优点[5]。张成林等[6]为检测燃气管道内部设计了一种基于离散卡尔曼滤波算法的高精度捷联惯性定位系统,其定位误差最大不超过4.7%。然而惯性器件的定位误差会随着时间的推移不断累积,因而在实际应用中大多采用与其他传感器相结合的组合定位导航方式对惯导数据进行修正[7]。刘鸿宇[8]以微惯性测量单元与里程轮相结合完成地下管道机器人定位,有效提高了管线定位精度,但在工作过程中管道内壁往往存在焊缝或积存杂物等致使里程轮出现打滑甚至脱离与管道接触,从而影响测速导致定位误差增加。向泓铭[9]为进行管道内部机器人的精准定位,融合视觉与惯性定位,解决了惯导误差积累问题。但是融合视觉定位依赖于信标建立,对于长直管道等无法建立信标的环境,难以利用周围环境来判断位置信息。此外,一些研究人员通过滤波算法来减小惯性导航的定位误差。P.Zhang[10]减少了由惯导系统和里程计安装位置以及比例因子引起的误差。Y.Huang[11]提出了一种用于里程计辅助惯性导航系统的卡尔曼滤波方法。实验结果表明,所提出的方法可以更好地估计从当前坐标系到初始坐标系的姿态矩阵。

为保证定位精度,减小误差积累,并解决上述文献中存在的实际问题,本文提出了一种基于扩展卡尔曼滤波算法的双惯导+地表编码器里程计融合定位算法。系统以两套惯导的距离为约束,结合地表编码器里程计测得蛇形机器人位移增量信息,再以扩展卡尔曼滤波算法建立管道探测蛇形机器人定位系统模型,以补偿单惯导定位随时间产生的累积误差,从而提高了管道探测蛇形机器人的导航定位精度,达到高精度导航定位的目的。

1 系统定位原理

系统硬件单元连接如图1所示。燃气管道探测蛇形机器人以行波运动在管道内部行走,惯导系统安装在“蛇身”,通过有线电缆将惯导解算信息传输到上位机监控中心,另外在信号传输线上加装一根尼龙绳并行。编码器里程计由地表上位于管道闸井入口处的绕线盘和旋转编码器组成,将尼龙绳缠绕于绕线盘上,随着蛇形机器人在管道内部的移动带动绕线盘转动,利用安装在绕线盘上的旋转编码器即可获得蛇形机器人在管道内部运行速度及位移增量。

根据两套惯导系统输出的姿态角解算出蛇形机器人从载体坐标系到参考坐标系的方向余弦矩阵。同时通过地表上编码器里程计解算出蛇形机器人在载体坐标系下的速度和位移增量,再利用方向余弦矩阵将其转换到参考坐标系下,并累计到两套惯导系统的初始位置上,获得双惯导系统在参考坐标系下的位置。将惯导系统初始位置作为状态量,编码器测得机器人位移增量作为控制量,惯导间的距离作为量测量引入扩展卡尔曼滤波器,经过扩展卡尔曼滤波获得两套惯导系统的位置,从而输出地下管道内部蛇形机器人位姿信息。融合算法定位原理如图2所示。

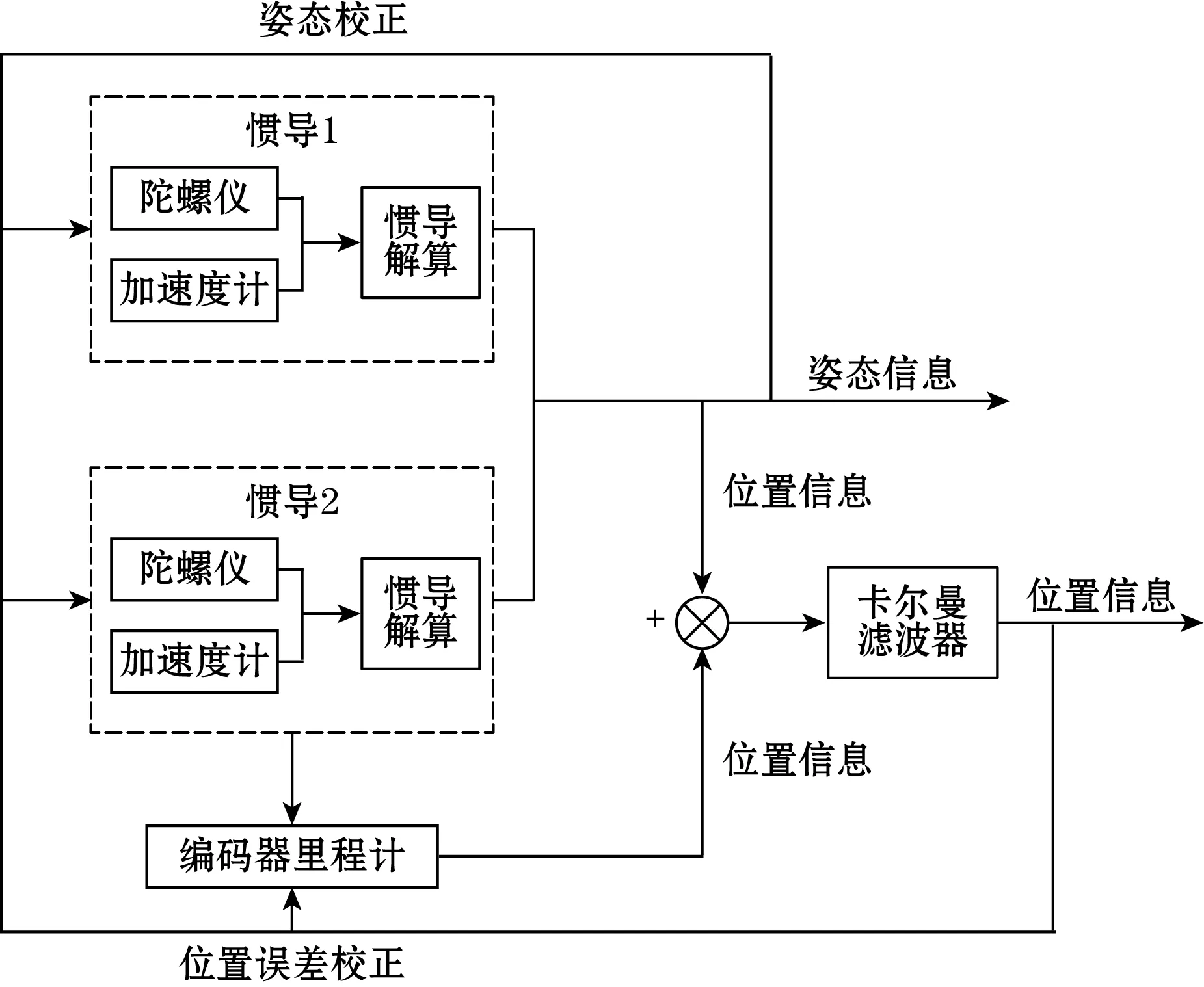
图2 融合定位算法原理

2 双惯导+编码器里程计融合定位算法模型

2.1 坐标系建立

建立管内蛇形机器人本体的数学定位模型[12],并建立坐标系,如图3所示。参考坐标系为东-北-天坐标系(O-XnYnZn),Xn指向北向,Yn指向东向,Zn垂直于Xn轴和Yn轴指向天向。载体坐标系(O-XbYbZb)以蛇形机器人机身几何中心为坐标原点O,其中Xb为机器人的轴向方向,其与管道的轴向方向一致,Yb垂直于管道轴向,Zb为垂直方向。k为惯导系统采样时间。

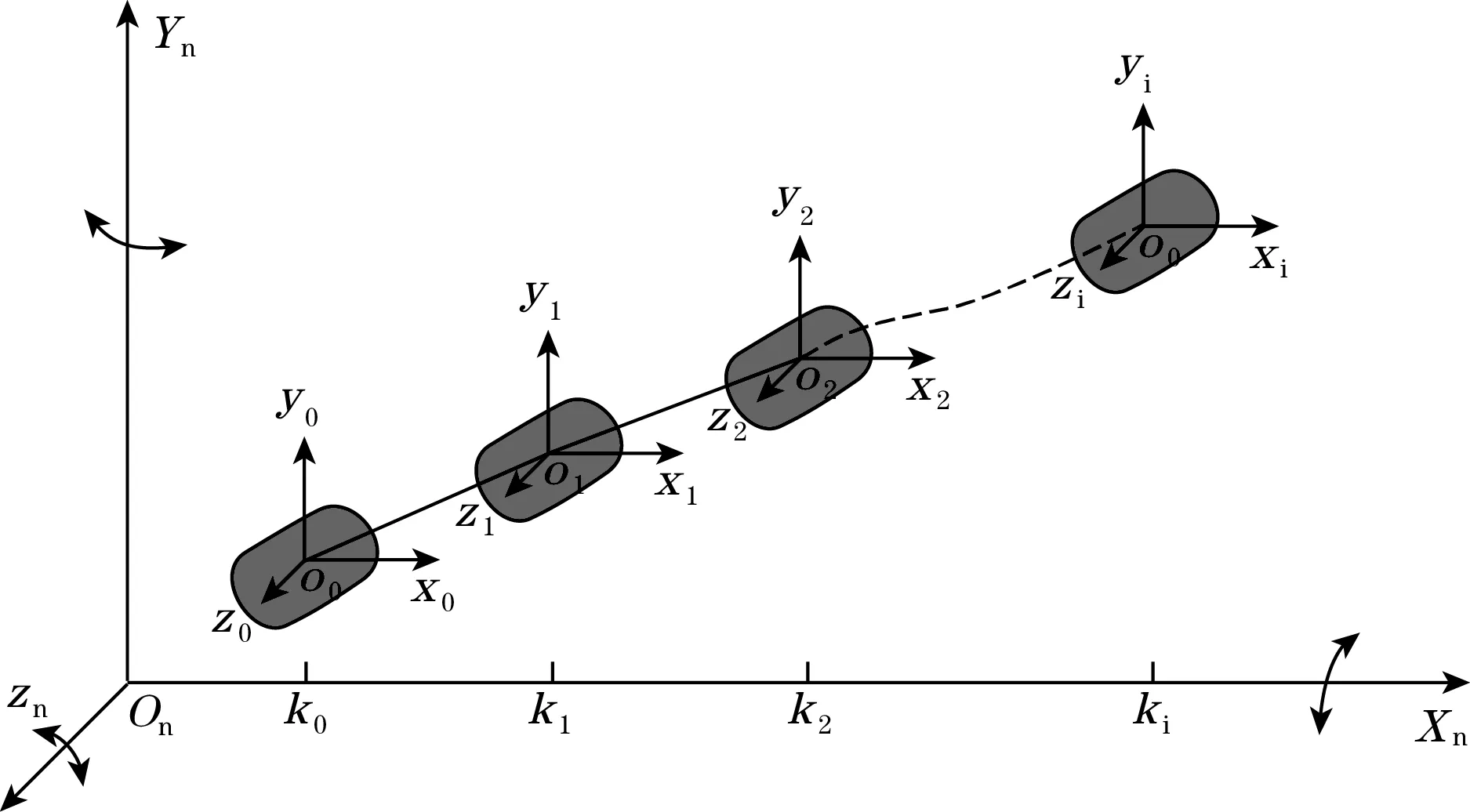
图3 管道内蛇形探测机器人的数学模型及运动轨迹

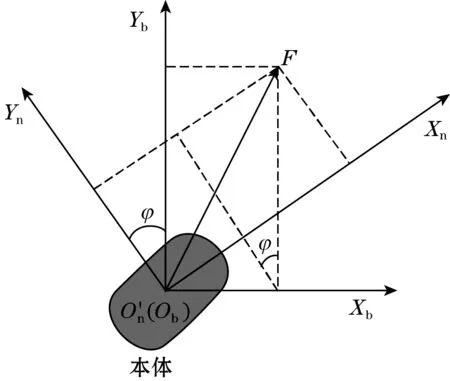
图4 蛇形机器人本体简化模型

假设{Ob}绕负z轴旋转φ度角,坐标系定义为{rXb′,rYb′,rZb′},表示如下:

(1)

得到其变换矩阵如下:

(2)

同理,围绕X旋转θ角,围绕Y轴旋转γ角得到的变换矩阵如下:

(3)

(4)

(5)

(6)

将惯导系统的角度信息输入到式(6)中,便可以描述蛇形机器人姿态信息。

2.2 扩展卡尔曼滤波模型

(7)

(8)

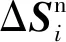
(9)

则惯导系统在参考坐标系下的参考位置如下:

(10)

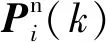
选取两套惯导系统在参考坐标系下的位置坐标为状态量X(k),X(k)表达式如下:

X(k)=[N1(k)E1(k)U1(k)N2(k)E2(k)U2(k)]

(11)

设计扩展卡尔曼滤波器状态方程如下:

X(k+1)=Φ(k+1|||k)X(k)+D(k)+W(k)

(12)

式中:X(k)为系统在k时刻的状态,X(k)∈Rn;W(k)为k时刻系统过程白噪声;Φ(k+1|||k)为k时刻到k+1时刻的状态转移矩阵,其表达式如下:

Φ(k+1|||k)=diag[1 1 1 1 1 1]

(13)

D(k)为k时刻控制矩阵,其表达式如下:

(14)

使两套惯导系统固定在机身上,选取2个惯导之间的距离r12为卡尔曼滤波器观测量Z(k):

Z(k)=[r12]

(15)

r12表达式如下:

(16)

假设k时刻的观测噪声为V(k),离散非线性系统观测方程可以表示为

Z(k)=h[k,X(k)]+V(k)

(17)

式中Z(k)为对应状态的观测信号,Z(k)∈Rm。

Z(k)=H(k)X(k)+V(k)

(18)

其中量测矩阵H(k)为h(*)的雅可比矩阵,忽略高阶余项可得其表达式为

(19)

根据上述建立的状态方程和量测方程,对线性化后的模型建立扩展卡尔曼滤波递推方程如文献[14]所示,即可根据机器人前一时刻位置信息得到当前时刻位置信息,从而获得机器人的定位信息。

3 方法验证

3.1 仿真实验

为验证融合方案的定位效果,本节采用MATLAB软件对机器人的运动轨迹进行仿真。仿真参数设置:仿真总时长为5 000 s,周期1 s,设置编码器测得机器人运行速度为0.1 m/s,设置蛇形机器人上两套惯导的坐标:惯导1坐标为(0,0,0),惯导2坐标为(0.5,0,0)。两套惯导系统的姿态角误差均设置为由0.5°的常值误差、频率1 Hz、振幅0.5°的周期性误差和方差为0.25的白噪声组成的简化模型。惯导1姿态角误差漂移方向为正,惯导2为负。

图5、图6为蛇形机器人航向角和俯仰角均为0°时,双惯导+编码器里程计融合定位算法处理前后单惯导的定位轨迹与理想定位轨迹的对比。从图5、图6可以看出,随着运行距离增加,单惯导定位误差逐渐增大,具有明显的误差累计现象,而融合定位算法的定位轨迹,随着运行时间的增加其误差累积现象不明显,定位轨迹与理想定位轨迹重合度高,其定位误差相较于单惯导定位误差明显减小。

(a)东北平面定位轨迹

(a)东北平面定位轨迹

单惯导定位误差与融合定位算法的定位误差对比如表1、表2所示,可看出融合定位方法的定位误差均小于单惯导定位方法。

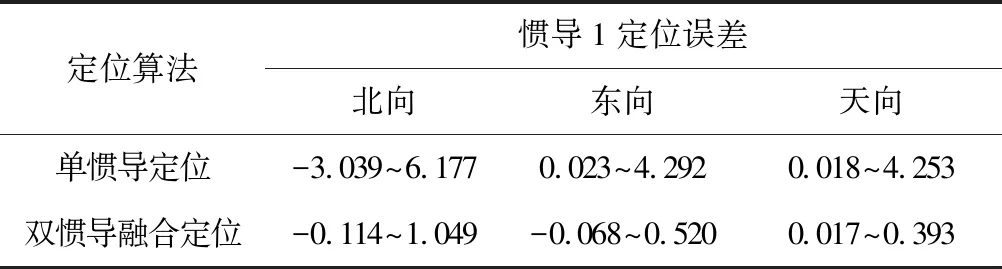
表1 惯导1及融合定位算法的定位误差比较 m

表2 惯导2及融合定位算法的定位误差比较 m

为测试惯导安装距离与仿真航向角对定位结果的影响,采用球概率误差(SPE)[15]评估仿真实验定位精度,仿真结果如图7和图8所示。

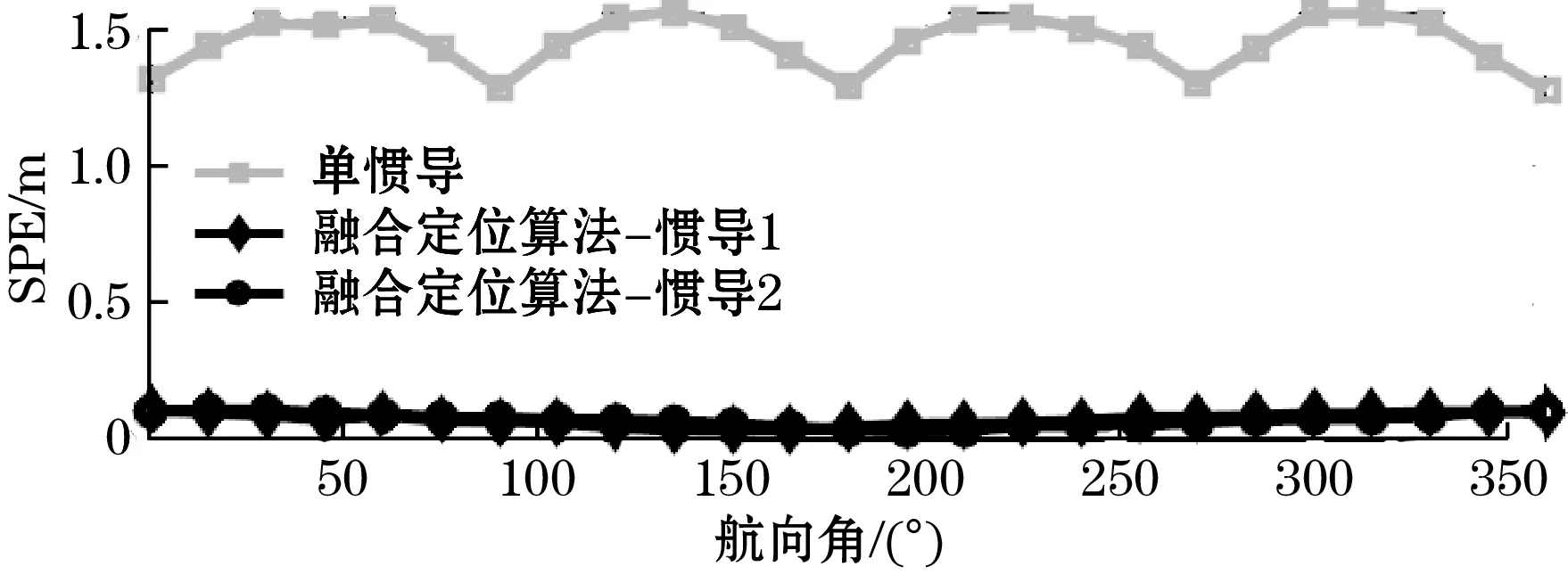
图7 航向角对定位算法的精度影响

图8 惯导安装距离对定位算法的精度影响

球概率误差(SPE)计算式如下:

SPE=0.51(σE+σN+σU)

(20)

式中:σE为东向定位误差均方根;σN为北向定位误差均方根,σU为天向定位误差均方根。

图7为蛇形机器人俯仰角为0°时航向角对定位精度的影响。图7中,随着航向角的变化,单惯导的球概率误差为1.36～1.71 m,而融合定位算法的球概率误差为0.05～0.11 m。图8为蛇形机器人俯仰角、航向角均为0°时惯导之间的安装距离对定位精度的影响。可以看出,单惯导的定位球概率误差约为1.35 m,而融合定位算法的定位球概率误差约为0.11 m。实验结果证明,基于双惯导+编码器里程计的融合定位算法能够在机器人不同运行条件下以及惯导不同的安装位置下均减小定位误差。

3.2 实验验证

实验平台搭建如下:管道探测蛇形机器人样机、JY901惯性导航模块、绕线盘、旋转编码器、5 V直流稳压电源、装有上位机系统的笔记本电脑以及通讯线缆若干等。惯导1安装在蛇形机器人机身原点,其定位信息可以准确代表机器人位置信息,惯导2坐标为(0.1,0,0)。实验地点为学校内部,总长度261 m,机器人按顺时针方向前进。行驶路线如图9所示。

图9 蛇形机器人行驶路线规划图

在实验过程中蛇形机器人以行波、匀速的方式向前行进。两套惯导模块实时同步采集蛇形机器人运行时产生的加速度、角速度等信息。将蛇形机器人尾部的安全牵引尼龙绳缠绕于绕线盘上,通过旋转编码器获得蛇形机器人运行速度及位移增量,并通过有线电缆将惯导系统和编码器采集到的信息上传至上位机终端进行解算。经过单惯导算法和融合定位算法各自进行解算,将解算得到的数据进行拟合可以分别得出其定位轨迹,如图10所示。

图10 蛇形机器人坐标系下轨迹图

由图10可以看出,双惯导融合算法解算的轨迹较单惯导定位算法导航偏差更小,解算的轨迹更加贴合实际的行驶轨迹,且双惯导融合方案解算的定位轨迹尾端与真实的蛇形机器人定位轨迹更加契合。2种算法定位误差如表3所示。

表3 2种定位算法的误差范围 m

从表3可以看出,该融合算法定位误差波动范围较小,其北向定位误差在-1.47～2.12 m之间,而单惯导定位算法北向定位误差在-3.65～11.82 m之间。双惯导定位算法东向定位误差在-2.04～2.33 m之间,而单惯导定位算法东向定位误差在-10.51～15.27 m之间。从东北两向的定位误差结果分析可知,双惯导+编码器里程计融合定位较单惯导定位准确率高,更加适用于蛇形机器人在地下燃气管道内部定位。

4 结论

为保证管道探测蛇形机器人定位精度,提出了基于扩展卡尔曼滤波的双惯导+编码器里程计融合算法。论文主要工作内容如下:

(1)为获取地下管道内部蛇形机器人精准定位信息,提出了一种融合算法。以惯导系统的位置为状态量,融合机器人运动过程中位移增量作为状态方程控制量进行误差补偿,将两套惯导之间的距离作为观测量,建立扩展卡尔曼滤波方程。改善了单惯导随时间产生的误差累积现象。

(2)为测得管道内部机器人单位时间内位移增量,使用绕线盘+旋转编码器构成的编码器里程计,有效避免了传统轮式里程计产生的打滑误差。

(3)为了验证算法的可靠性,利用MATLAB进行仿真,并搭建实验平台进行实验验证。实验结果证明双惯导+编码器里程计融合算法相较于单惯导定位精度更高,可以有效降低单惯导长时间工作导致的累积误差,且在机器人运行条件和惯导间安装距离变化时均有效,能够为蛇形机器人在地下燃气管道内部检测时提供可靠的定位信息,为实际工程应用奠定了基础。