基于柔性导向机构的重力分量传感器开发

姜传星,江 福,杨志军

(广东工业大学,省部共建精密电子制造技术与装备国家重点实验室,广东广州 510006)

0 引言

打磨机器人因其柔性好,运动范围大,已广泛应用于航空装备、高铁内饰、汽车船舶制造、五金卫浴等领域[1]。根据机器人动力学介绍,在空间中对机械臂最大的干扰力为重力[2]。机器人臂在对抗重力时,载荷和手臂连杆部位的质量会产生重力力矩。为了减少机器臂在运动控制中受到重力力矩的影响,有必要通过重力补偿来提高执行机构的定位精度。根据能量利用的不同,重力补偿可分为被动重力补偿和主动重力补偿[3]。

天津大学的宋轶民等选用定刚度螺旋拉簧为重力补偿元件,构造了静柔度半解析模型,大幅度降低了重力造成的机构末端的影响[4]。文献[5]研究了非零自由长度弹簧的腿部矫形器的重力平衡设计,提出了一种基于重量平衡机构的内凸轮设计。这2种方法虽提高了能量效率和平滑的动态,但与此同时系统中增加了质量、惯性和体积。由于机械手尺寸的限制,这一方法在一些应用场合中受到了限制[6-7]。

文献[8]利用在控制末端执行器的位置加装六维力传感器,得到在约束方向上接触力并结合末端位姿角进行计算,使机器人能够对接触力产生及时反馈,从而对控制电路所产生的力进行调整。此类传感器因价格昂贵,较难大规模使用。广东工业大学何伟崇利用加速度传感器测得装置前端重力,并且配合姿态传感器测得装置的轴线与水平面夹角,从而进行重力分解的计算[9]。华中科技大学的马文超利用陀螺仪对装置轴向方向上的角速度,通过积分来得到装置轴向方向和水平面之间的倾角,从而计算出重力的补偿值[10]。这2类方法需要多种传感器进行配合使用,多种信号因响应误差,会增加系统的速度响应。

对此,本文提出了一种基于柔性铰链导向机构的重力分量传感器,利用双平行柔性铰链机构和全桥式应变片电路的组合来获取实际运动过程中机械手臂所受到的重力,根据不同的运动角度来计算出重力分量,进而在机械手臂控制环节中进行重力补偿。工作原理是,当柔性铰链与重力方向平行时,2组柔性铰链处于拉伸,另外2组处于压缩状态,全桥电路刚好互相抵消,输出有效应变为0。当柔性铰链水平时,受到的弯曲变形最大,为90°或者-90°情况,分别记为±n。在其他位形情况下,重力在双平行柔性铰链组成的导向机构的分量为重力乘于当前应变值n,无需先测量俯仰和偏摆2个角度再进行2个三角函数的乘积,可节省计算时间。另外,此方法还能测量用于加速引起的惯性力部分,比现有的重力补偿更加准确。实验结果表明:重力角度的数值计算与计算结果非常接近,最大误差为2.5%。该传感器为机械臂的重力补偿提供新的配件选择,在有效地提高机械臂控制精度的同时,降低开发成本。

1 柔性铰链机构导向设计

根据机器人力控重力补偿是要获得在导轨导向方向上的重力分量。现有的方法主要是通过角度传感器,获得偏摆和俯仰角度,然后通过2次三角函数计算乘积得到重力分量。因此,重力传感器的本质是获得重力在导轨方向上的分量。从受力分析角度来看,传感器在导轨上的分量随着角度的变化,范围为(-1,1)。比如,导轨与重力方向垂直时,这时候重力在导轨方向的分量为0,当导轨与重力方向一致时,重力在导轨方向的分量为1或者-1。为了实现上述效果,设计出双平行柔性铰链机构,每片柔性铰链上均贴一片应变片,组成全桥式电路(图1)。

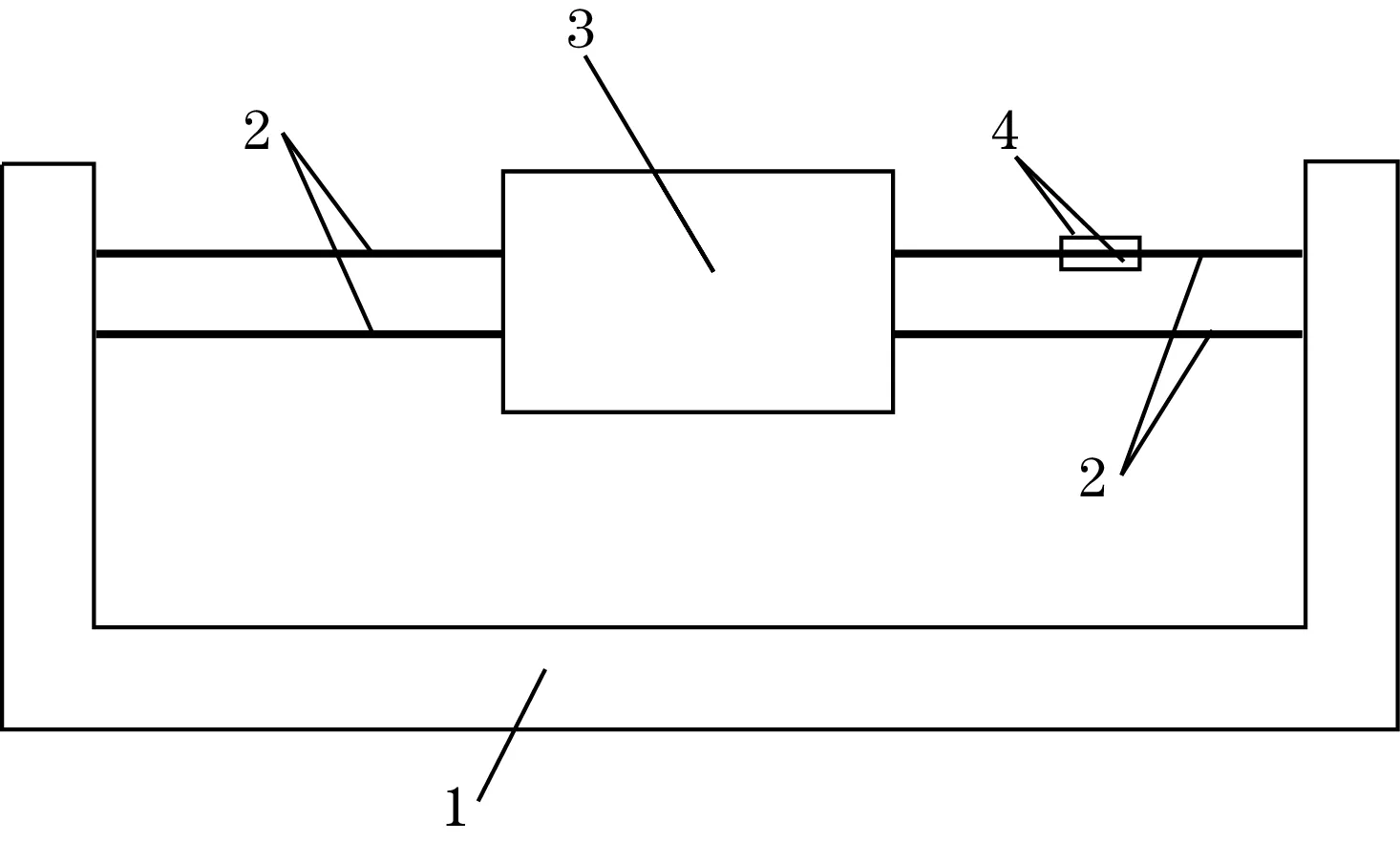
(a)柔性导向机构

当柔性铰链片与重力垂直时,柔性铰链在重力作用下呈最大的位移(图1(b)),此时桥式应变片产生最大的输出。当柔性铰链与重心平行时,在重力作用下,上部柔性铰链产生拉伸变形,下部柔性铰链产生压缩变形(图1(c)),此时桥式差分应变电流的值相互抵消,输出值最小。在任意位置,柔性铰链的受力可以分解为产生弯曲的力和产生拉压变形的力(图1(d)),其中,产生弯曲的力为mgsinθ,产生拉压的力为mgcosθ。由图1(c)可知,产生拉压的力被桥式差分电路互相抵消,对输出值没有影响。因此,当导轨方向与重力方向成夹角在±90°范围内变化时,桥式应变电路的输出值会在-1～1之间变化。

1.1 导向刚度

影响柔性铰链工作性能的因素主要包括刚度、运动行程以及工作时的最大应力[11]。而导向机构最主要的性能体现就是刚度,由于弹片式柔性铰链是非线性变形,其拉伸力引起的刚度变化可通过以下公式进行计算:

(1)

(2)

(3)

式中:Mz为力矩;Fx、Fy分别为x、y方向上的力(此处是将力和位移无量纲化处理);E为杨氏模量;I为惯性矩;l为柔性铰链的长度;θ为位移方向上的转角。

导向端轴向位移(运动行程)Δx=0,转角θ=0,整理可得:

f=(12+1.2ρ)uy

(4)

z=-(6+0.1ρ)uy

(5)

(6)

将式(6)代入式(4),可得:

(7)

(8)

(9)

1.2 导向机构的拉伸变形

(10)

(11)

因此可得到轴向拉伸变形为

(12)

2 应变片检测电路设计

将电阻应变片粘贴在柔性铰链上,其中R1、R2、R3、R4分布如图2所示,作为电桥的4个臂,通过导线接入AD8226仪表放大器,最后通过数模转换芯片得到电压。当柔性铰链发生形变时,应变片电阻发生变化,应变片电阻由电桥平衡时的Rx变为Rx+ΔR,这时通过读取电压Ui,再根据Ui与ΔR的关系测出ΔR与柔性铰链形变之间的关系,从而计算出柔性铰链的形变量。

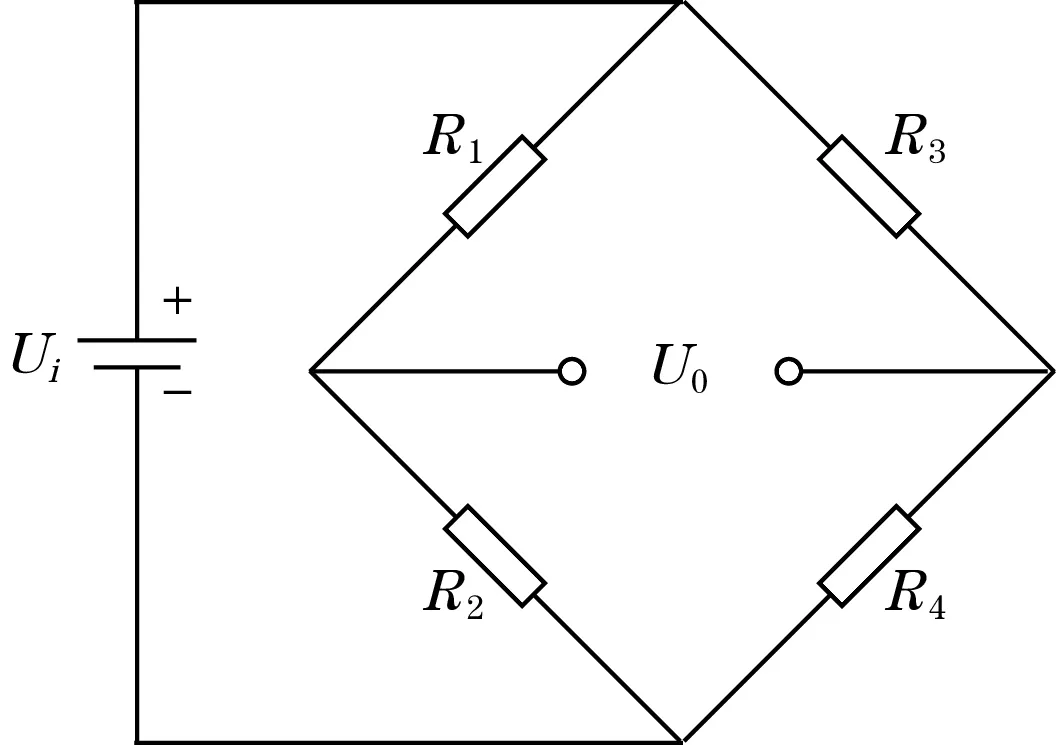
图2 应变片电路

(13)

式中:Ks为灵敏系数;ε为应变片形变量。

3 传感器的标定

根据传感器受力,选取-90°、0°和90°3个方向获取传感器的AD值。测试得到以上角度的AD值分别为796、965和1 134。±90°与0°的AD差值分别为±169。说明1倍重力引起的变形为169,记为T。

重力分量检测过程中,每隔10°,计算传感器的AD值,记为n。由重力分量计算式(14),代入传感器标定的数据可得式(15):

F=gsinθ

(14)

式中:F为重力分量;g为重力加速度;θ为计算的传感器角度。

(15)

式中:n0为0°时的AD值;T为1倍重力引起的变形量。

将计算值与测量值均列入表1。由表1可以看到,计算值与测量值之间的相对误差仅为2.25%。计算方法简单,在计算重力分量时,可由式(16)得到重力补偿量,重力分量曲线如图3所示。

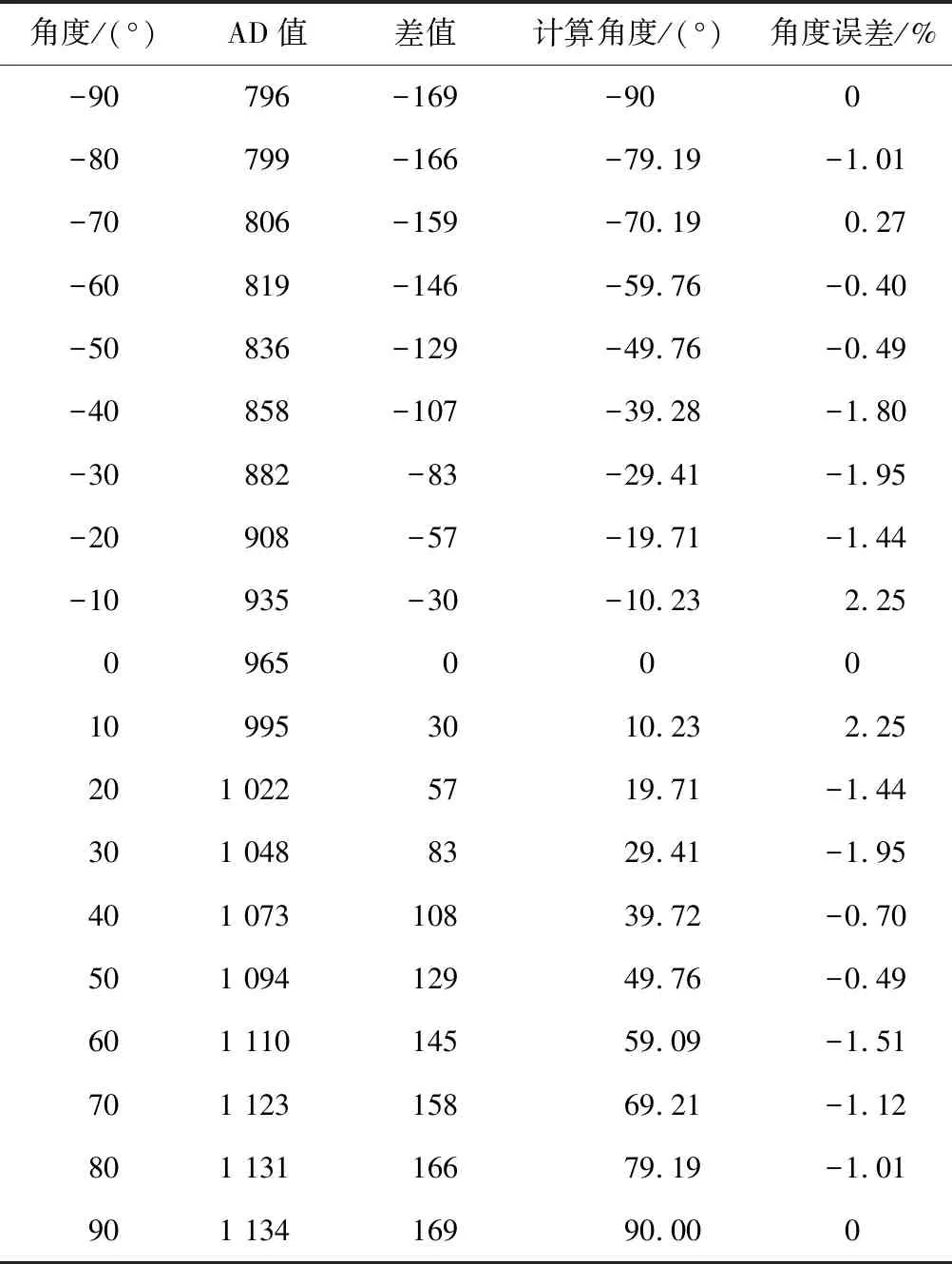
表1 每隔10°AD计算值与测量值对比表

图3 重力分量曲线图

(16)

式中:m为传感器质量;n为当前角度AD值;n90为90°时的AD值。

当比值f大于1,表明产生了加速度,这样就能把质量产生的动态加速度分量也考虑进去,比角度传感器的测量结果更加精确。

4 结束语

用有限元方法对传感器进行受力分析,验证了本文设计的传感器性能可靠,能够利用柔性铰链的拉压形变来抵消非工作方向力的影响,仅需将柔性铰链垂直放置(标记为0°)和正反水平放置(标记为±90°),即可获得在-90°～90°作用范围内的任意角度分量的值,最大误差仅为2.5%的分辨力,满足了打磨装置的重力补偿要求。