一类广义二项指数和的四次均值

孟园园

(西北大学 数论及其应用研究中心,陕西 西安 710127)

设p是一个奇素数,χ是模p的任意狄利克雷特征。对任意整数k>h≥1,m以及n且(n,p)=1,广义二项指数和S(m,n,k,h,χ;p)定义为

S(m,n,k,h,χ;p)=

其中:e(y)=e2πiy;i2=-1。

广义二项指数和在解析数论研究中起着非常重要的作用,许多重要的数论问题都与之密切相关,如素数分布以及华林问题等。因此,不少数论专家和学者对S(m,n,k,h,χ;p)的各种性质进行了研究,取得了一系列有意义的研究成果。例如,Zhang H等[1]证明了对于任意奇素数p,有

(1)

式中,n为整数且满足(n,p)=1。

Zhang W P等[2]利用初等和解析的方法得到了如下结论。

(2)

最近,Zhang W P等研究了S(m,n,3,1,χ0;p)的六次幂均值计算问题[3],并证明了对任意奇素数p和整数n且(n,p)=1,有恒等式

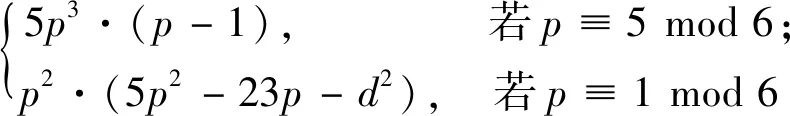
(3)

式中:4p=d2+27·b2;d是由d≡1 mod 3唯一确定。

另一方面,以Chen L等研究了二项指数和S(m,1,4,1,χ0;p)的四次均值的计算问题[4],并得到了计算公式

(4)

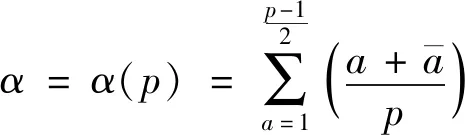
p=α2+β2=

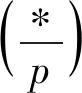
一些与指数和相关的结论可参阅文献[6-15],这里不再一一列举。

从式(1)～式(4)可以看出,所有这些论文的内容都只涉及S(m,n,k,h,χ;p)中的h=1。通过对文献的检索,到目前为止还没有发现关于广义二项指数和S(m,n,k,2,χ;p)的四次均值的相关研究内容。这说明当k>h=2时,研究工作是具有相当难度的,不易得到理想的结果。

本文利用初等和解析方法以及一些同余方程解的个数等性质研究了2k次幂均值的计算问题,并给出了当p≡3 mod 4以及k=2时该式的一个精确的计算公式。

即就是证明下面的结果。

定理1设p是素数,p≡3 mod 4,那么,有

式中,模p的六次特征定义为存在模p的特征χ1,使得χ=χ16。

由定理1可推出以下推论。

推论1设p是素数,p≡3 mod 4,那么对模p的任意非主偶特征χ,有渐近公式

16p3+O(p2)。

注1本文只讨论了p≡3 mod 4的情况。如果p≡1 mod 4,暂时不能得到一个令人满意的结果。因为无法得到下式的精确值或平非凡的上界估计。

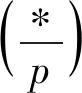
另一方面,假定χ是模p的一个非主偶特征。否则其均值为零。事实上,如果χ是模p的一个奇特征,即χ(-1)=-1,那么可以得到

所以有

此外,考虑这种形式的四次均值的主要原因是研究单个四次均值不能得到一个精确的计算结果。这种形式的和抵消了在单个均值中无法计算的部分。

1 若干引理

为了完成定理1的证明,需要借助3个简单的引理。这些引理的证明需要一些初等数论和解析数论的知识[5-6]。

引理1设p是一个奇素数,χ为模p的任意非主偶特征,有恒等式

证明由模p的同余方程解的性质可知

(5)

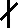
(a2+b2)(a2-1)(b2-1)≡0 modp,

当且仅当a2≡1 modp或者b2≡1 modp时成立。这种情况下注意到χ(-1)=1,有

8(p-1)-8=8(p-2)

(6)

若p≡1 mod 4,那么a2+b2≡0 modp,1≤a,b≤p-1,有2(p-1)个解。a2-1≡0 modp有2个解。这种情况下,有

8(p-2)+4(p-1)-16=

12(p-3)

(7)

结合式(5)～式(7),引理1得证。

引理2设p是一个奇素数。则对于模p的任意非主偶特征χ,有恒等式

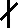
(8)

由经典高斯和的性质可知

(9)

(10)

(11)

同样,也有

(12)

(13)

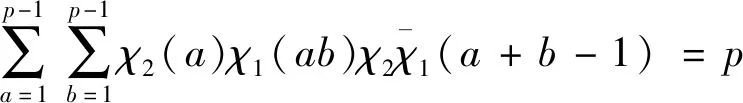
(14)

结合式(8)～式(14),得到

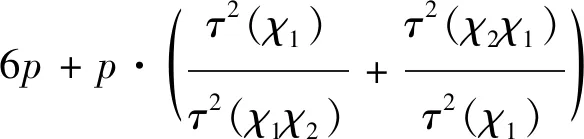
(15)

若3|(p-1),设整数r满足r≠1,r3≡1 modp。若χ(r)≠1,则

或者

(16)

若χ(r)=1,令χ=χ16,ψ是模p的六阶本原特征。由模p的六阶本原特征的性质和式(8)～式(14)的证明思路,有

O(p)

(17)

结合式(15)～(17),有

引理2得证。

引理3设p是一个奇素数,p≡3 mod 4。对于模p的任意非主偶特征χ,有恒等式

引理3得证。

2 定理1的证明

现在应用第1节中的3个引理来完成定理1的证明。对任何整数n,显然有三角恒等式

对任意整数n且(n,p)=1,有

由模p的简化剩余系的性质,有

(18)

同样,也有

(19)

由引理3的证明方法也有

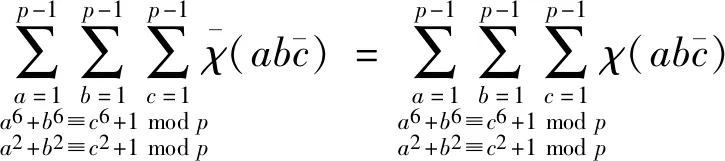
(20)

和

(21)

若χ不是模p的一个六次非主偶特征,结合式(18)～(21),引理1～3,有

16·p2·(p-2)

(22)

若χ是模p的一个六次非主偶特征,有

16·p2·(p-2)+O(p2)=

16p3+O(p2)

(23)

结合式(22)和式(23),定理1得证。

3 结语

本文的主要结果是给出了一类二项指数和四次均值的一个精确的计算公式。

式中:p≡3 mod 4;χ是模p的一个非主偶特征。

同时,研究的结果也为高次二项指数和均值的计算问题提供了一些新的有效方法,这些工作将对相关问题的研究发挥积极的作用。

致谢:作者对导师张文鹏教授的悉心指导表示衷心感谢!