斜风作用下三塔悬索桥颤振稳定性研究

张新军,周 楠,郁 聪,赵晨阳

(浙江工业大学 土木工程学院,浙江 杭州 310023)

当前,国内外悬索桥广泛采用双塔结构。为满足目前跨海桥梁建设的需求,悬索桥必须采用更大的跨径跨越既深又宽的海峡以降低锚碇和下部结构的建造成本,其中无共用锚碇的多塔多跨悬索桥成为最具可行性的解决方案之一。已有研究表明:在一定条件下,多塔悬索桥可能比其他桥梁结构形式更适合于桥址,即使跨度达到2 000～3 000 m也是一种经济的解决方案[1]。在多塔多跨悬索桥中,尤以三塔悬索桥更受到青睐和关注,屡屡在国内外大跨度桥梁方案设计中被提出,并相继在江苏省泰州市、安徽省马鞍山市和武汉市鹦鹉洲等跨越长江大桥中得到成功应用。三塔悬索桥边塔虽然能够从锚碇处引出的背索得到有效约束,但是中塔的纵向约束比较薄弱,因此结构整体刚度小于传统的双塔悬索桥,成为一种更加柔性的结构体系。由于三塔悬索桥结构刚度较小,其对风的作用更加敏感。风对桥梁结构的作用包含风的静力作用和动力作用两个方面,前者主要是静风荷载作用下结构的变形和稳定性问题,而后者主要是动力风荷载作用下结构的颤振和抖振问题,其中颤振是一种发散性振动,一旦形成会对桥梁结构造成如1940年美国塔科马悬索桥的风毁事故,因此成为三塔悬索桥抗风研究的首要问题。迄今为止,对于三塔悬索桥的系统研究主要集中在静力性能、结构体系、中塔合理刚度和动力性能等方面[2-5],同时也开展了一些颤振方面研究[6-10]。已有的三塔悬索桥抗风研究都是针对法向风情况,即风的来流方向与桥轴线正交。大跨度桥梁在确定桥位时,通常使桥轴线的法向偏离桥址处的主风向,内地山区或复杂地形地区的桥梁其所受的自然风方向复杂多变,沿海地区桥梁经常遭受风向多变的台风侵袭,现场风速观测也表明桥梁所受强风的作用方向大多偏离桥跨法向,即实际情形中桥梁通常遭受斜风作用。已有分析和风洞试验研究表明在斜风作用下双塔悬索桥的颤振稳定性最差[11]。因为三塔悬索桥的结构刚度比传统的双塔悬索桥更小,所以迫切需要研究斜风作用下三塔悬索桥施工至成桥全过程的颤振问题,以确保其抗风安全性。

目前,学者们针对双塔悬索桥开展了为数不多的斜风下的颤振稳定性研究,主要采用平均风分解法和斜截面法这两种方法。平均风分解法将斜风分解为与桥跨方向垂直的余弦分量和与桥跨方向平行的正弦分量,通常忽略正弦分量的影响,采用传统方法求得余弦分量下的颤振临界风速后反算出斜风下的颤振临界风速,该方法通常称为“余弦法则”,其隐含着法向风作用下结构颤振稳定性最低的假定。根据余弦法则,颤振临界风速随着风偏角的增大而逐渐提高。Zhu[12]通过斜风下青马大桥颤振稳定性的风洞试验发现不同风攻角下颤振临界风速随风偏角的增大均呈现波动变化特征,且在斜风情况下达到最小值。针对当前悬索桥加劲梁大多采用流线型箱形截面,朱乐东等[13]通过斜节段模型风洞试验研究了不同风攻角下流线型箱形截面在斜风作用下的颤振稳定性,发现在非零风攻角下箱形截面的流线形变差,颤振临界风速随着风偏角增大而波动变化,最小值一般出现在斜风作用情形。高伟[14]以南京长江四桥为研究对象,基于斜风下节段模型风洞试验对扁平闭口箱梁颤振稳定性进行研究,发现在非零风攻角下虽然随风偏角增大颤振临界风速呈现波动变化特征,但是没有明显的规律,在斜风下颤振临界风速达到最小值,同法向风情况相比降幅约5%。Zhu等[15]针对扁平闭口箱梁、扁平π型梁、双主梁和桁架等典型主梁断面开展斜节段模型试验,发现颤振临界风速随着风偏角的增大呈波浪形变化,且变化规律在很大程度上取决于断面形状和风攻角,在±3°风攻角范围内斜风作用使得上述4种断面的颤振临界风速分别降低6%,2%,8%和7%,最小颤振临界风速对应的风偏角在4°～15°。为改善1 088 m主跨桁架加劲梁悬索桥的颤振稳定性,Zhu等[16]通过斜节段模型风洞试验研究了上下中央稳定板对斜风下颤振稳定性的影响,发现大多数情况下风偏角居于5°～10°时,颤振临界风速最低。虽然前期主要通过试验和数值分析方法开展了斜风下双塔悬索桥成桥状态的颤振稳定性研究,但是在数值分析时都采用多模态耦合的方法,忽略了静风作用的影响。已有研究表明静风作用对双塔悬索桥成桥尤其是施工状态的颤振稳定性影响显著[17]。对于结构更加柔性的三塔悬索桥,斜风下成桥和施工状态的颤振稳定性如何则未见相关的研究报道。为此,运用考虑静风作用和全模态耦合影响的斜风作用下大跨度桥梁三维精细化颤振分析程序(Nflutter-sw),以泰州长江大桥为工程背景,分析了斜风下成桥状态和加劲梁从跨中向两侧桥塔对称架设全过程的颤振稳定性,揭示了斜风和静风作用对成桥和施工状态三塔悬索桥颤振稳定性的影响,为三塔悬索桥的抗风研究提供理论参考。

1 斜风下大跨度桥梁精细化三维颤振分析程序

斜风作用下三塔悬索桥的颤振稳定性分析采用斜风下大跨度桥梁三维精细化颤振分析程序Nflutter-sw[18],该程序基于斜节段的静风荷载和自激气动力计算模型,考虑斜静风作用引起的结构刚度变化以及作用于结构上的静风荷载和自激气动力的非线性变化、三维效应(简称静风效应)及全模态耦合效应,通过外部风速循环和内部频率迭代的增量迭代法求解结构的颤振临界风速,程序计算流程如图1所示。

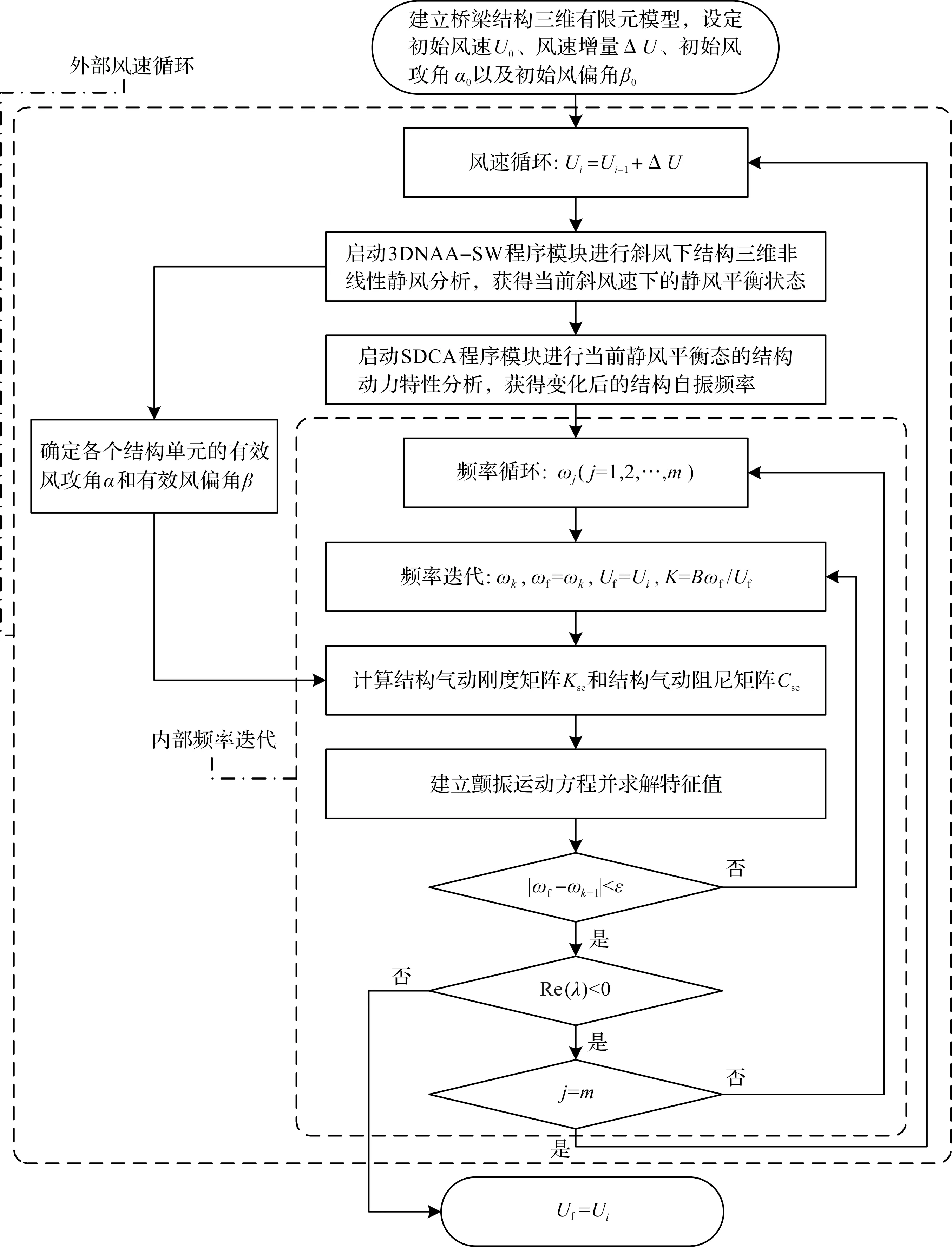
图1 Nflutter-sw程序计算流程

2 桥梁简介

泰州长江大桥的实景、立面布置图和加劲梁标准截面如图2所示。其主桥为三塔两跨吊连续钢箱梁悬索桥,桥跨布置为390 m+2×1 080 m+390 m[19]。加劲梁采用流线型钢箱梁,宽39.1 m,桥面中心线处梁高3.5 m。主缆矢跨比为1∶9,两侧主缆中心距为34.8 m,吊杆纵桥向间距为16 m。边塔采用钢筋混凝土门式框架桥塔,纵桥向呈单柱形,塔高178 m。中塔采用钢结构,横桥向为门式框架结构,纵桥向呈人字形,塔高194 m。加劲梁与中塔之间设置纵向弹性索。

3 斜风作用下三塔悬索桥成桥状态颤振分析

由于泰州长江大桥未进行斜风下主梁节段模型风洞试验,鉴于该桥主梁与南京长江三桥主梁极为相似,在此引用了南京长江三桥主梁成桥状态斜节段模型风洞试验测得的气动力参数[20]开展斜风下三塔悬索桥的颤振分析。为了说明引用的合理性,在法向风(0°风偏角)下,分别采用南京长江三桥与泰州长江大桥的气动力参数[19],采用Nflutter-sw程序计算得到不同初始风攻角下的颤振临界风速,并与泰州长江大桥节段模型风洞试验结果进行对比,结果如表1所示。由表1可知:法向风下各初始风攻角下采用南京长江三桥和泰州长江大桥气动力参数得到的颤振临界风速基本一致,说明南京长江三桥主梁成桥状态气动力参数能够很好地反映泰州长江大桥成桥状态的颤振稳定性,分析是可行的。另外,程序计算与该桥节段模型风洞试验结果也比较相符,表明Nflutter-sw计算程序是可靠的。

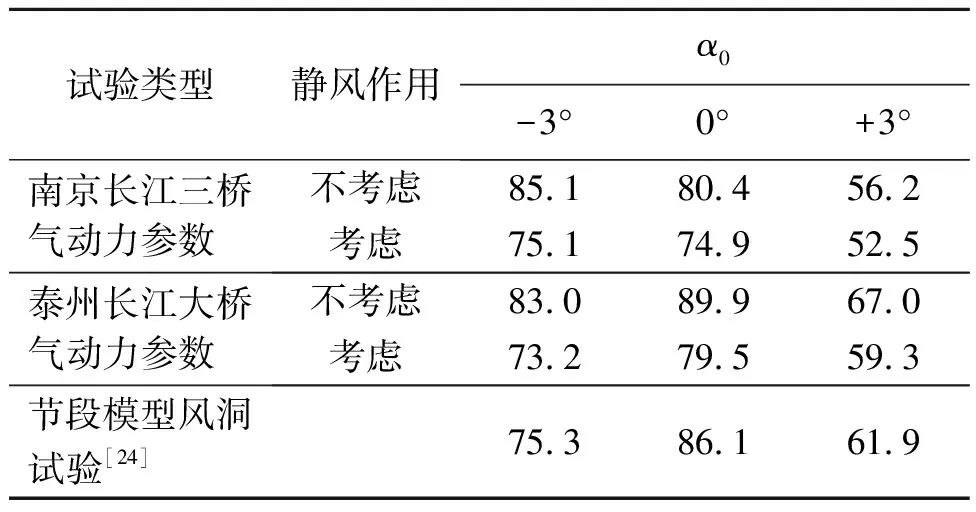
表1 不同气动力参数计算的颤振临界风速

为了探究斜风和静风作用对三塔悬索桥成桥状态颤振稳定性的影响,在0°和±3°初始风攻角和0°～25°初始风偏角下,进行不同初始风攻角α0和初始风偏角β0组合工况的颤振分析。各初始风攻角下颤振临界风速Uf随初始风偏角增大的变化情况如图3所示。

图3 各初始风攻角下颤振临界风速随初始风偏角增大的变化情况

由图3可知:不同风攻角下,颤振临界风速虽然随风偏角增大的变化趋势各不相同,但是均呈波动起伏变化特征,并非如斜风分解法所述的单调递增的变化趋势,最低颤振临界风速分别出现在10°(-3°风攻角),20°(0°风攻角)和0°(+3°风攻角)风偏角下,说明斜风作用对三塔悬索桥的颤振稳定性更为不利。同一风攻角下,考虑和不考虑静风作用的颤振临界风速随风偏角增加的变化趋势则总体一致,说明静风作用除影响颤振临界风速外,并不会改变其变化趋势。为了探究静风作用对颤振临界风速的影响,静风作用对颤振临界风速的影响率如表2所示,各初始风攻角和风偏角下的静风作用影响率ηw计算式为

表2 静风作用对颤振临界风速的影响率

(1)

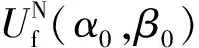
为了揭示斜风作用对颤振临界风速的影响,斜风作用对颤振临界风速的影响如表3所示。表3给出了各初始风攻角下的最低颤振临界风速、斜风作用影响率ηβ以及斜风与静风综合作用影响率ηwβ,表达式分别为

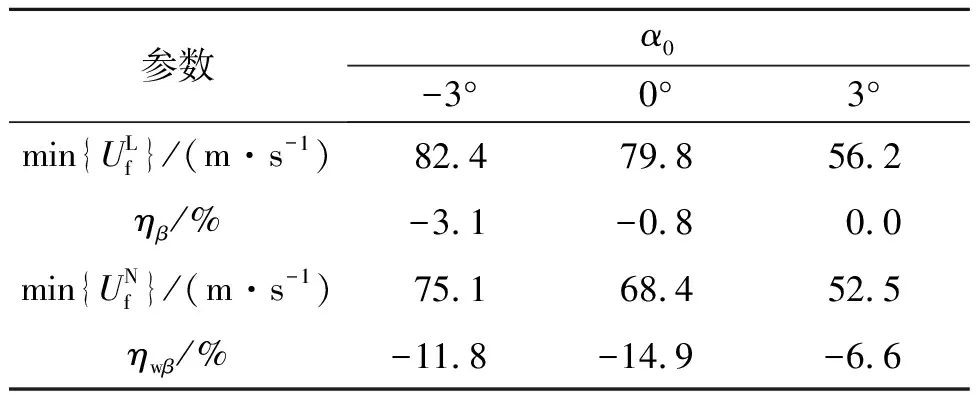
表3 斜风作用对颤振临界风速的影响

(2)

(3)

由表3可知:相较于法向风作用,斜风作用下线性颤振临界风速最大降幅达3.1%,3个攻角下的平均降幅为1.3%,说明斜风作用对三塔悬索桥颤振稳定性的影响不显著。在静风作用影响后,最低颤振临界风速进一步减少,考虑静风和斜风作用的综合影响后各初始风攻角下的颤振临界风速最大降幅达14.9%,3个初始风攻角下的平均降幅为11.1%,可见静风和斜风综合作用对三塔悬索桥成桥状态颤振稳定性的影响显著,颤振分析时需要准确考虑。

4 斜风作用下三塔悬索桥施工状态颤振分析

三塔悬索桥加劲梁架设主要有如图4所示的两种顺序,即由跨中至两侧桥塔对称拼装和分别从边塔和中间桥塔向跨中对称拼装。泰州长江大桥的加劲梁架设采用由两个主跨跨中分别向中塔和两侧边塔对称拼装的架设顺序,笔者将针对这种架设顺序开展斜风作用下架设全过程的颤振分析,揭示主梁架设期颤振稳定性的变化趋势,探讨斜风和静风作用对三塔悬索桥施工状态颤振稳定性的影响。

图4 三塔悬索桥桥面主梁架设顺序

为了说明采用南京长江三桥施工状态主梁气动力参数分析泰州长江大桥主梁架设期颤振稳定性的可行性,在0°初始风攻角的法向风作用下,采用Nflutter-sw程序计算各个主梁架设期的颤振临界风速,并与泰州长江大桥施工过程全桥气动弹性模型风洞试验结果[24]对比,结果如图5所示。考虑到铰接法施工的三塔悬索桥施工期加劲梁段间的临时连接刚度与成桥状态相比严重削弱,主梁架设期颤振分析时加劲梁的竖向和横向弯曲刚度以及扭转刚度分别取成桥状态对应刚度的10%,50%,80%[10]。由图5可知:采用南京长江三桥施工状态主梁气动力参数分析得到的主梁架设过程颤振稳定性变化趋势同试验结果基本相同,且数值也非常接近,说明了南京长江三桥施工状态主梁气动力参数能够较好地反映泰州长江大桥施工状态的颤振稳定性,同时再次说明了Nflutter-sw程序的可靠性。

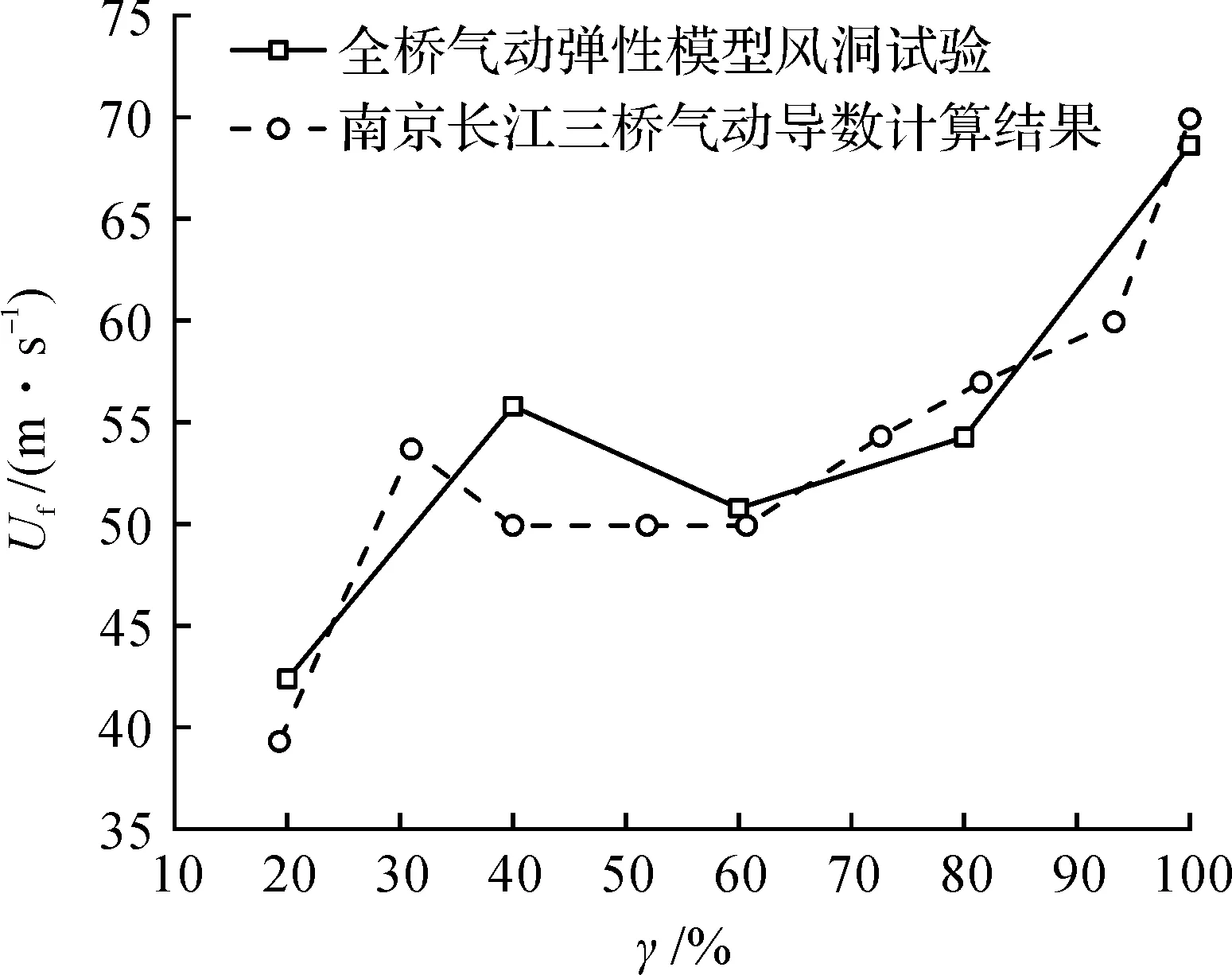
图5 0°风攻角法向风下主梁架设过程颤振临界风速的变化趋势

在-3°,0°和+3°初始风攻角下,运用Nflutter-sw程序进行了0°～25°初始风偏角范围内主梁架设全过程的颤振分析,颤振临界风速随主梁拼装率γ增加的变化情况如图6所示。图6中虚线为不考虑静风作用的颤振临界风速;实线为考虑静风作用的颤振临界风速。由图6可知:各初始风偏角下主梁架设过程考虑和不考虑静风作用的颤振临界风速变化规律基本类似,均呈现先急剧增大再急剧减小最后缓慢增长的变化规律,说明静风作用不会改变三塔悬索桥施工状态颤振稳定性的演变趋势。主梁架设期颤振临界风速在主梁拼装率30%附近达到第一个峰值,在主跨合拢后达到第2个峰值,但主梁拼装率在20%以下和40%～80%的颤振临界风速均较低,成为颤振稳定性薄弱的主梁架设期。

图6 斜风作用下主梁架设过程颤振临界风速的变化趋势

各主梁架设阶段的颤振临界风速随着初始风偏角的增大呈波动变化特征,并非如斜风分解法所述的单调变化趋势,主梁架设过程考虑和不考虑静风作用的最低颤振临界风速minUf的变化情况如图7所示。由图7可知:各风攻角下主梁架设过程考虑和不考虑静风作用的最低颤振临界风速的变化规律基本一致,说明静风作用虽然不会改变主梁架设期颤振稳定性的变化规律,但是会影响颤振临界风速值,此外最低颤振临界风速均在0°和5°初始风偏角下出现。-3°初始风攻角下,静风作用使得主梁架设过程的颤振临界风速略有增加,但增幅不大,最低颤振临界风速均出现在5°初始风偏角下;0°初始风攻角下,静风作用的影响明显降低了主梁架设过程的颤振临界风速,最低颤振临界风速以5°初始风偏角下出现最多,其次是法向风情况;+3°初始风攻角下,静风作用使得主梁架设过程的颤振临界风速有明显降低,最低颤振临界风速主要出现在0°初始风偏角下,其次是5°初始风偏角。

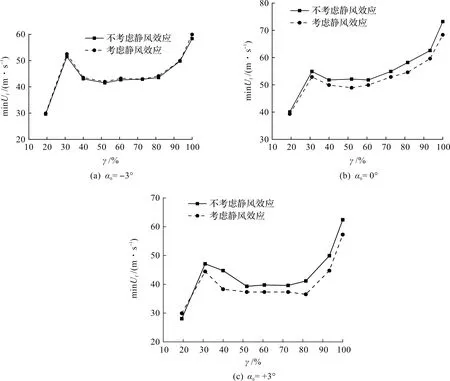
图7 斜风作用下主梁架设过程最低颤振临界风速变化情况

为了清楚地了解斜风和静风作用对主梁架设过程颤振稳定性的影响程度,表4给出了主梁架设过程斜风和静风作用对颤振临界风速的影响率。由表4可知:各初始风攻角下斜风和静风作用对主梁架设过程颤振临界风速的影响规律有所不同,-3°初始风攻角下主要受斜风作用影响,静风作用的影响非常有限,0°和+3°初始风攻角下的影响规律则与之相反。与法向风情况相比,斜风作用使得各初始风攻角下主梁架设过程的颤振临界风速都有明显的下降,各初始风攻角下受斜风作用的影响最大降幅分别达到了20.5%(-3°),20%(0°)和10.2%(+3°),主梁架设全过程的平均降幅分别为15.5%(-3°),4.4%(0°)和1.8%(+3°),与表3的成桥状态相比斜风作用对主梁架设过程的颤振稳定性影响更大。在此基础上,进一步考虑静风作用影响后,颤振临界风速的降幅进一步加大,各初始风攻角下受斜风和静风综合作用的影响最大降幅分别达到了19.5%(-3°),23%(0°)和14.7%(+3°),主梁架设全过程的平均降幅分别为14.5%(-3°),8.7%(0°)和8.6%(+3°),与表3的成桥状态相比,斜风和静风综合作用影响率明显增大,因此说明主梁架设过程中,三塔悬索桥颤振稳定性受斜风和静风综合作用的影响更显著,尤其需要重视斜风和静风综合作用产生的不利影响。

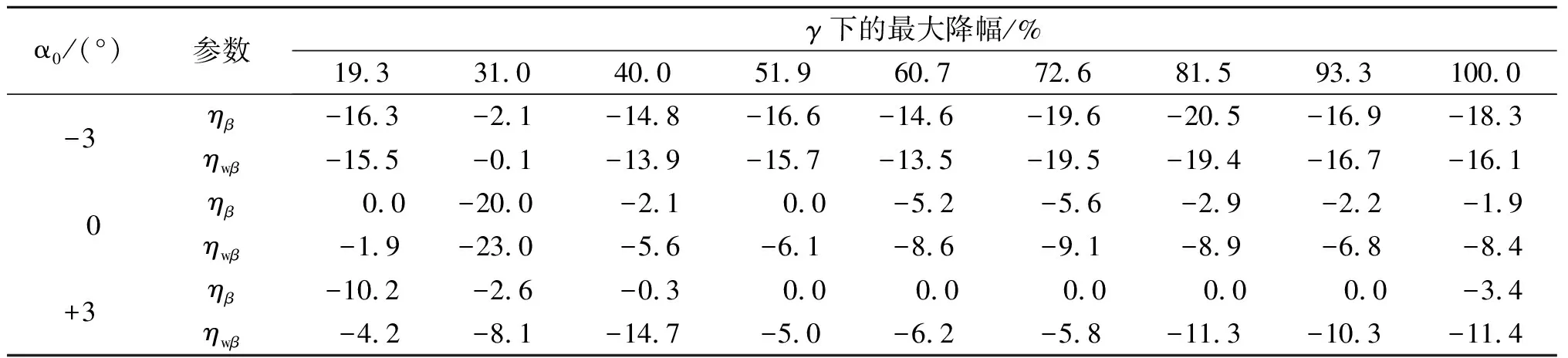
表4 主梁架设过程斜风和静风作用对颤振临界风速的影响率

5 结 论

以泰州长江大桥为例,采用考虑静风作用和全模态耦合效应影响的斜风作用下大跨度桥梁三维精细化颤振分析程序(Nflutter-sw),在0°和±3°初始风攻角以及0°～25°初始风偏角下,分析了成桥状态和加劲梁由主跨跨中向两侧桥塔对称架设全程的颤振稳定性,揭示了斜风和静风作用对三塔悬索桥颤振稳定性的影响,并得出了以下主要结论:三塔悬索桥成桥和施工状态的颤振临界风速都随着风偏角的增大呈现起伏变化特征,并非如平均风分解法所述的单调递增的变化规律,最低颤振临界风速大多出现在斜风情况;斜风,特别是静风作用,会显著降低三塔悬索桥成桥状态的颤振稳定性,静风作用导致3个初始风攻角下的颤振临界风速平均降幅为6.4%,斜风和静风共同作用则进一步劣化桥梁的颤振稳定性,与法向风情况相比,3个初始风攻角下颤振临界风速的平均降幅达11.1%,影响显著;斜风和静风作用虽然均不会改变三塔悬索桥加劲梁架设过程颤振稳定性的演变规律,但是都会导致施工状态颤振临界风速的进一步降低,各初始风攻角下斜风作用使得主梁架设全过程的颤振临界风速分别平均降低了15.5%(-3°),4.4%(0°)和1.8%(+3°),而斜风和静风的共同作用使得主梁架设全过程的颤振稳定性进一步降低,各初始风攻角下主梁架设全过程的平均降幅分别达14.5%(-3°),8.7%(0°)和8.6%(+3°),影响更为突出。因此,三塔悬索桥成桥特别是施工状态颤振分析必须综合考虑斜风和静风作用及其产生的不利影响。